Effect of Rib Stiffness on Stability of Submerged Ring-stiffened Functionally Graded Cylindrical Shells
2019-01-09
(Civil Engineering School,Henan University of Science and Technology,Luoyang 471023,China)
Abstract:The effect of rib stiffness on stability of submerged ring-stiffened functionally graded cylindrical shells was studied.Based on the Donnell thin shell theory,the total potential energy expression of the ring-stiffened cylindrical shell under hydrostatic pressure was established.Then,the stability equation of ring-stiffened functionally graded cylindrical shell was derived by using energy expression.The buckling critical load of ring-stiffened functionally graded cylindrical shell under hydrostatic pressure could be obtained by solving the stability equation.The proposed analysis method was validated by comparing the results in the literatures.By using numerical examples,the effects of power-law exponents,constituent materials,shell dimensions,types of ribs and rib arrangement on the buckling critical load were illustrated.The results show that the rib stiffness has the most important influence on the stability of ring-stiffened functionally graded cylindrical shells.
Key words:stiffened functionally graded cylindrical shell;buckling critical load;rib stiffness;hydrostatic pressure
0 Introduction
Due to the advantages of reducing weight and increasing strength,the ring-stiffened functionally graded(FG)cylindrical shells have been widely used in aerospace,marine engineering and other fields.The stability evaluation of ring-stiffened FG cylindrical shell has become more and more important research direction in the design of submerged structure.A number of studies on the stability of ring-stiffened isotropic cylindrical shells and ring-stiffened FG cylindrical shells have been made so far[1-13].The calculation formula for the critical load of ringstiffened cylindrical shells can be derived by using energy method[2].Bodner[3]studied the overall stability of submerged ring-stiffened cylindrical shells.Chen et al[4]presented an analysis method to predict the critical load of submerged ring-stiffened cylindrical shells.Chen[5]discussed the influence of the ring-stiffened parameters on the buckling critical load of the shell structure and introduced the strain energy factor to analyze the interaction between the rib and the shell.Wu et al[6]studied the effect of geometric parameters of ribs on the lateral sta-bility of ring-stiffened cylindrical shells.Wang[7]discussed the effect of rib spacing on the stability of cylindrical shells.The influence factors of the critical pressure of ring-stiffened FG cylindrical shell were discussed by Liang et al[8].Bai et al[9]analyzed the effect of rib stiffness and rib position on buckling critical loads of isotropic shell structures.Some other related researches have been carried out[10-12].However,due to the non-uniformity of the functionally graded material in the thickness direction,the research on the ribs stiffness of the ring-stiffened FG cylindrical shells under hydrostatic pressure is still rarely implemented,and the relevant research literature is very limited.
Based on the Donnell thin shell theory,the energy method is used to derive the characteristic equation of the overall instability of the ring-stiffened FG cylindrical shells under hydrostatic pressure.The buckling critical load of the cylindrical shell can be obtained by solving the characteristic equation in this paper.Firstly,the proposed calculation results have been compared with those in the literature to verify the validity and correctness of the calculation method.Secondly,the importance of rib stiffness in the study of cylindrical shells stability has been revealed by examples.Finally,the influence of rib stiffness on the buckling critical load of ring-stiffened FG cylindrical shells under hydrostatic pressure has been analyzed.
1 Mechanical model
Considering a ring-stiffened cylindrical shell with radius R,length L,rib spacing l,thickness h is as shown in Fig.1.The reference surface is taken to be the middle surface of the cylindrical shell where an orthogonal coordinate system(x,θ, )z is fixed.The x,θ and z are the axial coordinate,circumferential coordinate and radial coordinate,respectively.Q is hydrostatic pressure.
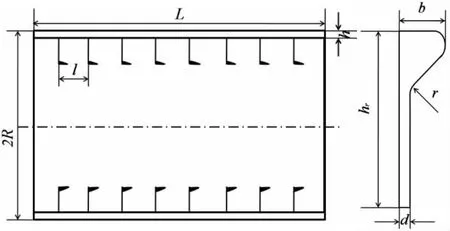
Fig.1 Geometry of ring-stiffened cylindrical shell and stiffener
Assuming that the shell and the ribs have the same compositional material,the equivalent Young’s modulus and Poisson’s ratio of FG cylindrical shells are expressed as follows:

From these equations,when z=h/2,E=E2,v=v2,and when z=-h/2,E=E1,v=v1.The material properties vary continuously from material 2 at the inner surface of the FG cylindrical shell to material 1 at the outer surface of the cylindrical shell.P is power law exponent,0≤P≤∞.
2 Theoretical formulation
When the ring-stiffened FG cylindrical shell is unstable,the boundary condition of the cylindrical shell can be considered as simply supported boundary condition.The displacement function of the ring-stiffened FG cylindrical shell can be written as:

where uij,vijand wijare the arbitrary constants,i is wave number in the circumferential direction,j is half wave number in axial direction.
Based on the Donnell thin theory,the geometrical equations of cylindrical shells can be given as:
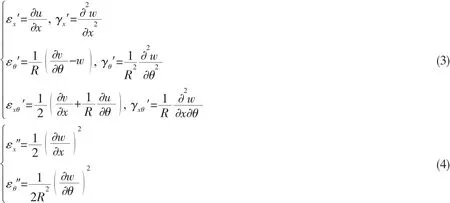
According to the Hooke’s law,the corresponding stress and bending moment can be defined as:
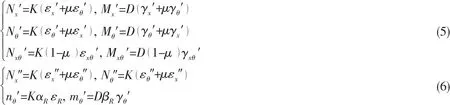
where K=Eh/(1- μ2),D=Eh3/12(1- μ2),αR=EAR/K,εR=εθ′-zRγθ′,βR=EI/D,ARis the crosssectional area of rib,zRis the distance between neutral axis of ribs and shell,I is bending inertia moment of rib with the shell effect.
According to the thin shell theory,the membrane solutions of cylindrical shell under the pre-buckling stress and state can be expressed as:

To determine the buckling critical load,the Rayleigh-Ritz method is used.The total potential energy of the ring-stiffened FG cylindrical shell is calculated as follows:

It is minimized with respect to unknowns uij,vij,wijas follows:

Then,the destabilizing characteristic equation of ring-stiffened FG cylindrical shells under hydrostatic pressure can be derived as follows.

The buckling critical load of the ring-stiffened FG cylindrical shell under hydrostatic pressure can be obtained by solving Eq.(10).
3 Numerical results and discussion
In order to verify the correctness and validity of the proposed calculation method,the calculation results of the buckling critical load of cylindrical shells of degenerate isotropic ringstiffened(ball flat steel)are given in Tab.1.The comparisons in the references show that the proposed results have good performance.

Tab.1 Comparison of the results of the buckling load of ring-stiffened cylindrical shells under hydrostatic pressure
In this chapter,the influence factors of the stability of ring-stiffened(ball flat steel)FG cylindrical shells have been studied(as shown in Figs.2-6).Here,the outer surface material of ring-stiffened FG cylindrical shell is stainless steel,and the inner surface material is zirconia.The material parameters of stainless steel and zirconia are:E2=2.077 88×1011Pa,ν2=0.317 756,E1=1.68×1011Pa,ν1=0.3[13].The parameters of the cylindrical shells are defined as h/R=0.01,P=1,j=1,l/R=1,L/R=20.
Fig.2 shows the curves of the buckling critical loads of ring-stiffened FG cylindrical shells with different power law exponents P.It can be seen that the buckling critical load of ring-stiffened cylindrical shells decreases with increasing of the power law exponent when P<5.However,when P>5,the buckling critical load is almost constant.The buckling critical load of the cylindrical shells increases significantly with increasing of the rib stiffness.The effect of power law exponent on buckling critical load decreases with decreasing of the rib stiffness.It can be seen from Fig.2,The buckling critical load of the cylindrical shell can be improved by increasing the rib stiffness.
Fig.3 shows the curve of the buckling critical load of ring-stiffened FG cylindrical shell with different material compositions.Here,the ball flat steel is 20a.As shown in Fig.3,the buckling critical loads of ring-stiffened cylindrical shells all decrease with increasing the L/R,however,the reduction extent is different.When L/R<5,the critical load drops quickly;when L/R=5~10,the buckling critical load begins to stabilize;when L/R>10,the buckling critical load is almost constant.When the material composition of the cylindrical shell changes from stainless steel/Si3N4to Ti-6Al-4A/zirconia,the maximum growth rate of buckling critical load is about 93%.

Fig.2 The buckling critical load of ring-stiffened FG cylindrical shell under hydrostatic pressure with different power-law exponents
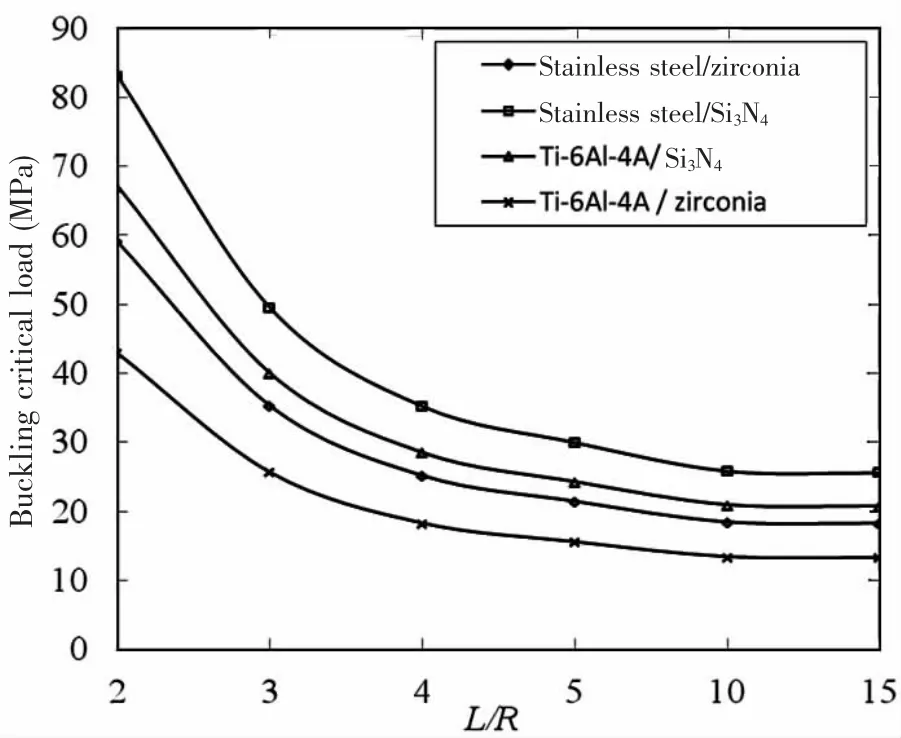
Fig.3 The buckling critical load of ring-stiffened FG cylindrical shell under hydrostatic pressure with various material components

Tab.2 The buckling critical load(MPa)of ring-stiffened cylindrical shells under hydrostatic pressure with different thickness-radius ratios
Tab.2 shows the results of the buckling critical load of ring-stiffened FG cylindrical shells with different thickness-radius ratios(h/R).As shown in Tab.2,the buckling critical load increases with increasing of the h/R.However,the buckling critical load decreases with increasing of the L/R.For h/R=0.005 and h/R=0.01,the maximum growth rate of buckling critical load of the ring-stiffened cylindrical shells is about 70%,when L/R=4~10,the growth rate shows a gradually decreasing trend,when L/R>10,the growth rate is only 30%.
Fig.4 shows the buckling critical load curve of ring-stiffened FG cylindrical shells with different ribs.According to the curves in the Fig.4,when L/R≤10,the rib type has the most significant effect on the buckling critical load;the change rule of the buckling critical load of the shell without rib is nearly the same as the shell with rib.However,the buckling critical load of the ring-stiffened FG cylindrical shell is obviously larger than that of the non-rib cylindrical shells.For example,the buckling critical load of 22a ball flat steel is much larger than that of 18a ball flat steel.When L/R=2,the growth rate of the buckling critical load is 60%.When L/R=2~10,the growth rate decreased at first and then increased with increasing of L/R;when L/R>10,the growth rate reaches double digits and becomes stabilized.
As shown in Figs.3-5,compared with material composition and shell dimensions,the rib stiffness has more significant effect on the buckling critical load.In order to show the influence of rib stiffness on buckling critical load,the FG cylindrical shells with different rib types and rib arrangement are considered in Figs.5-6.

Fig.4 The buckling critical load of ring-stiffened FG cylindrical shell under hydrostatic pressure with different types of ribs

Fig.5 The buckling critical load of ring-stiffened FG cylindrical shell under hydrostatic pressure with ball flat steel and rectangular steel

Fig.6 The buckling critical load of ring-stiffened FG cylindrical shells under hydrostatic pressure with different rib spacing-radius ratios
In Fig.5,the variation law of the buckling critical load of FG cylindrical shells with different ribs(ball flat steel and rectangular steel)has been studied under the same rib area AR=0.002 686 m2.The results show that the buckling critical load of cylindrical shells with ball flat steel is much larger than that of rectangular rib shells.The possible reason for this phenomenon is due to the bending inertia moment.
Fig.6 shows the curve of the buckling critical load of ring-stiffened FG cylindrical shells with different rib spacing-radius ratios(l/R).In Fig.6,the ball flat steel model is 22a.It is found that the buckling critical load decreases with increasing of the l/R;the buckling critical loads initially decrease rapidly and then slowly with increasing of the L/R;the buckling critical load is almost constant when L/R>10;the influence of the rib spacing on the critical load is mainly reflected in the case of small L/R.
4 Conclusions
(1)The buckling critical load of the ring-stiffened FG cylindrical shells under hydrostatic pressure is affected by the material composition,shell dimensions and rib types.However,the results show that the rib stiffness has more significant effect on the buckling critical load than the material components and shell dimensions.
(2)In general,the buckling critical load increases with increasing rib stiffness.However,when the rib stiffness reaches to a certain value,the buckling critical load is approximately constant with increasing rib stiffness.The value of buckling critical load can be increased by increasing rib stiffness and reducing rib space.Although the value of buckling critical load changes with rib stiffness and L/R,the variation laws of the buckling critical load with different rib stiffness are nearly the same.With the increasing of L/R,the buckling critical load first decreases and then becomes constant.
(3)The effect of the rib type on the buckling critical load of the ring-stiffened FG cylindrical shells under hydrostatic pressure is mainly reflected in the case of small L/R.The growth rate of the buckling critical load increases with increasing of the L/R.If the ball flat steel rib model changes from 18a to 22a,the growth rate of the buckling critical load is only about 60%when L/R≤3,the growth rate reaches double digits and becomes stabilized when L/R≥10.
(4)The buckling critical load can be increased by increasing h/R,and the growth rate of buckling critical load decreases with increasing of the L/R.When L/R≥10,the growth rate of buckling critical load is 70%.However,when L/R>10,the growth rate is only 30%.The effect of rib type on buckling critical load of cylindrical shells is more significant than that of h/R.
杂志排行
船舶力学的其它文章
- Dynamic Stability of Liquefied Cargo Ship in Waves
- Investigation on Time Domain Motions for Ship and Floating Structure and Coupled with Nonlinear Sloshing
- Overset Simulations of Submarine’s Emergency Surfacing Maneuvering in Calm Water and Regular Waves
- A Revised Method for Predicting Added Waves Resistance Based on Comparison of Theoretical and Empirical Results for VLCC Hull Forms
- 3D Nonlinear Hydroelastic Response and Load Prediction of A Large Bulk Carrier in Time Domain
- Strength Characteristics of Maraging Steel Spherical Pressure Hulls for Deep Manned Submersibles
