有限厚度含水层双排水盲沟渗流计算探讨
2019-01-08叶坤王贤能
叶坤,王贤能
(深圳市工勘岩土集团有限公司,深圳 518057)
1 引言
排水盲沟越来越多的用于公路、建筑地基等的排水工程中[1~7],其中有单排水盲沟、双排水盲沟、多排水盲沟等。目前排水盲沟渗流相关研究有两大重点问题:一是盲沟的排水量计算,二是盲沟排水后场地内的地下水位变化。其中,关于单排水盲沟渗流计算的相关研究已比较成熟,而对于双排水盲沟,甚至是多排水盲沟的排水量、水头分布等渗流计算的相关研究却鲜有报道。现有的研究成果中,双排水盲沟渗流分析常用的解析方法有水力学法和水动力学法。周华[8]综合了两种方法的特点,并适当简化了渗流条件,通过保角变换求解,提出了单沟和双沟渗流量及场地内剩余最高水位的计算方法。《公路排水设计规范》9.4节中给出了双排水盲沟排水量计算公式[9]。当然也可采用数值模拟的方法模拟双排水盲沟渗流的过程,直接由有限元软件得出双盲沟的排水量和水位变化结果。
本文以双排水盲沟为例,对比了上述3种双排水盲沟渗流计算方法,并以有限元为主要手段,讨论了不同盲沟间距、不同渗透系数、不同水位降深等对双排水盲沟渗流量及剩余水头差的影响。
2 双排水盲沟渗流计算的理论解
2.1 计算方法一
采用保用变换求解双沟渗流计算,简称“方法一”。
(1) 排水量计算
对称双排水盲沟模型剖面图如图1所示。假设排水盲沟充水断面呈矩形,沿水平方向进入盲沟底部的一条流线近似直线,整个渗流区域划分成上下两部分。上部分无压含水层内盲沟渗流量用水力学方法计算,可直接引用裘布依经典公式;盲沟底以下部分视为承压含水层,通过保角变换求解,得出简化后的渗流量精确计算公式,最后得到单侧单宽进入盲沟的渗流量为:
(1)
式中,φ为单侧的整体渗流阻抗系数,表示为:
(2)
式中,φ为渗流阻抗系数:
(3)
式中其余参数为:k1为沟底以上部分无压含水层的平均渗透系数(m/d);k2为沟底以下承压含水层的平均渗透系数(m/d);b为与湿周长度等效的矩形底宽的一半(m);H为原始水位线到沟底的距离(m);Ho为盲沟内的水位高(m,假设盲沟内始终充满水);T为沟底以下含水层的厚度(m);R为影响半径(m);lo为对称盲沟间距的一半。
各参数具体含意见图1所示。对称双排水盲沟双侧单宽渗流量为单侧的2倍,即为2Q。

图1 对称双排水盲沟一侧渗流计算剖面图
(2) 剩余水头高度Hx计算
图1中计算lo区间地下水最高水头Hm和外侧剩余水头高度Hx分布的公式分别为:
当x= -(lo+2b)时,
(4)
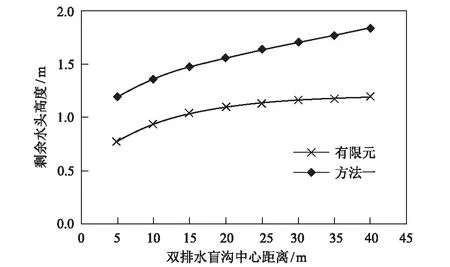
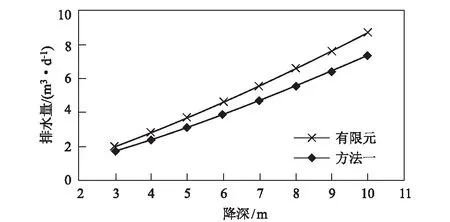
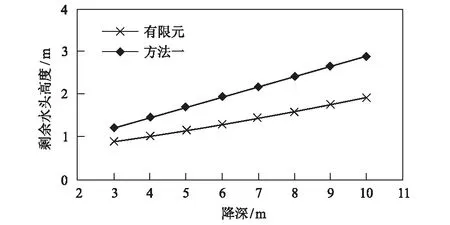
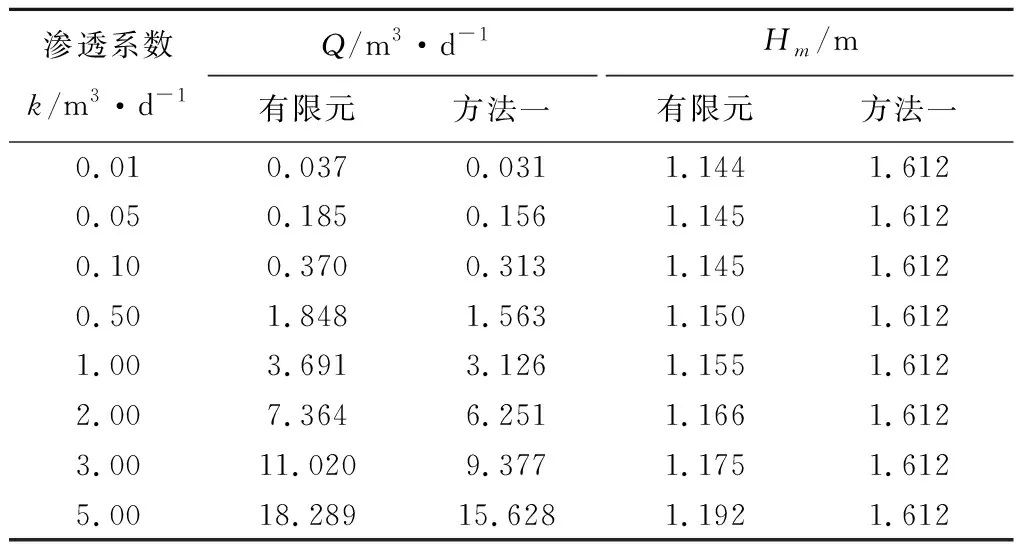
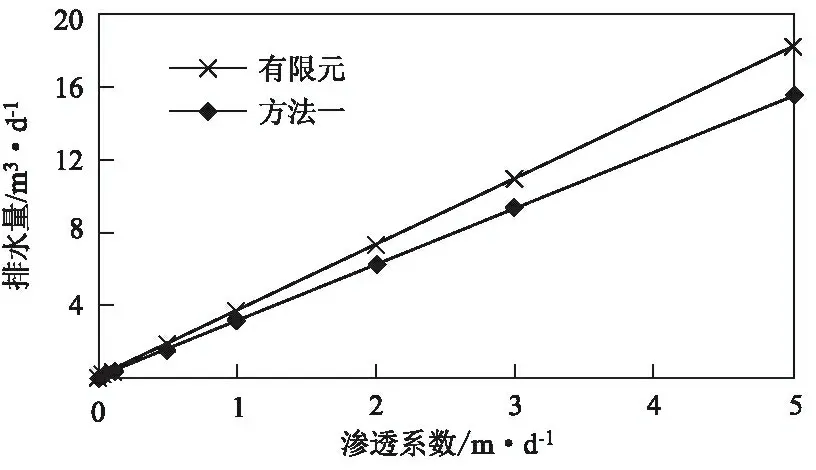
当-(lo+2b) (5) 当-2b≤x≤0时, Hx=Ho (6) 当0 (7) 其中, (8) (9) (10) 计算方法二为规范法计算[9]。对称双排水盲沟排水量规范法计算公式为: (11) 式中各参数含义同上。 本文采用MIDAS-GTSNX岩土有限元软件来模拟双排水盲沟的渗流计算。一般计算模型如图2所示。计算时,在模型两侧以及排水盲沟处设置给定水头边界;在模型底面、顶面,以及排水盲沟上的开挖面设置给定流量边界,流量为0,即为隔水边界。 图2 有限元计算模型及其边界条件示意图 已知排水盲沟截面尺寸为底宽1.0 m、高0.5 m,沟底埋深5.5 m;有限含水层厚度20 m,参透系数k=1.0 m/d;对称双排水盲沟的中线间距为30 m。盲沟排水渗流的影响半径R按库萨金公式计算[10]: (12) 式中,Sw为排水盲沟处地下水位降深,取Sw=5 m;k为渗透系数,k=1.0 m/d;h为含水层厚度,取h=20 m。计算得:R=44.7 m,取R≈45.0 m。 分别采用方法一、方法二计算排水量,并与有限元计算结果对比验证。对称双排水盲沟的已知条件汇总见表1。 表1 对称双沟单宽渗流计算参数汇总表 采用上述3种方法并代入参数计算得双排水盲沟排水量及剩余水头高度的计算结果见表2。 表2 对称双沟单宽渗流计算结果汇总表 注:方法二中暂无剩余水头高度的计算方法。 对称双排水盲沟的剩余水头高度的有限元计算结果与理论计算(方法一)结果见图3。 图3 对称双沟剩余压力水头方法一与有限元计算结果对比 由此可见,采用方法一与有限元的计算的排水量和剩余水头高度的结果都十分接近,而采用方法二的排水量计算结果远大于方法一和有限元的计算结果。说明采用方法一与有限元进行双排水盲沟渗流计算时,可以得到较为合理的结果,其结果具有一定的参考价值。 分别取盲沟中线间距为5 m、10 m、15 m、20 m、25 m、30 m、35 m、40 m,研究双排水盲沟不同间距对双盲沟渗流的影响。其余参数按计算实例取。计算结果见表3和图4、图5。 表3 不同盲沟间距的渗流计算结果汇总表 图4 双排水盲沟间距对盲沟排水量的影响 图5 双排水盲沟间距对剩余水头高度的影响 从上述图表的计算结果可知,双排水盲沟中线间距增大,会引起排水量的少量增加,其中有限元计算结果显示最大增幅为4%,而方法一计算结果显示最大增幅为27%。剩余水头高度增加幅度稍大,且方法一的计算结果明显大于有限元计算结果。另外,有限元结果显示:当双盲沟间距大于10~15 m时,剩余水头高度的增长趋势变缓,故在实际工程中若盲沟间距初步设计值大于15 m时,则可考虑再适当增大,以减小工程造价。 令降深Sw=H-Ho,并且Ho设为固定值0.5 m,分别取Sw为3 m、4 m、5 m、6 m、7 m、8 m、9 m、10 m,研究不同降深对双盲沟渗流计算的影响。本文假设降深变化不引起影响半径的改变。其余参数按计算实例取。计算结果见表4和图6、图7。 表4 不同降深的渗流计算结果汇总表 图6 降深对盲沟排水量的影响 图7 降深对剩余水头高度的影响 由上述计算结果可知,降深因素无论对排水量还是剩余水头高度都有较大的影响,且基本呈正比例关系。其中排水量与降深的比例系数为0.802~0.955,剩余水头与降深的比例系数为0.146~0.389。故从降深的角度来看排水量与剩余水头高度的计算结果,降深越小越好。 分别将参透系数设为0.01 m/d、0.05 m/d、0.10 m/d、0.50 m/d、1.00 m/d、2.00 m/d、3.00 m/d、5.00 m/d,研究不同渗透系数对双排水盲沟渗流的影响。其余参数按计算实例取。计算结果见表5和图8、图9。 表5 不同渗透系数的渗流计算结果汇总表 图8 渗透系数对盲沟排水量的影响 图9 渗透系数对剩余水头高度的影响 由计算结果可知,渗透系数的变化与排水量呈正比关系,其中有限元计算结果的比例系数为3.66,方法一计算结果的比例系数为3.13。而渗透系数的变化对剩余水头高度则没有影响。 排水盲沟可有效排除地基中的地下水以及侧向来水,是降低场内地下水位的一种有效方法。在排水盲沟设计中,需要进行渗流计算,以确定排水盲沟的排水量、间距、剩余水头高度等相关设计参数。本文通过对排水盲沟的相关计算公式的深入研究,将之与有限元计算结果进行对比,提出了可用于排水盲沟渗流量和剩余水头高度的计算方法;并分析了排水盲沟间距、水位降深、渗透系数这3个主要影响因素对双排水盲沟渗流计算的影响。 分析结果显示,有限元的排水量计算结果较大,剩余水头高度较小;而方法一的计算结果正好相反。因此,出于安全的角度考虑,在计算盲沟排水量时,建议参考有限元计算结果,而在计算剩余水头高度时,建议参考方法一的计算结果。在3个主要影响因素中,水位降深对双排水盲沟渗流的影响最大,且接近正比例关系;排水盲沟间距对排水量影响的敏感度相对较小,而对剩余水头高度影响相对较大;渗透系数则只对排水量有影响,对剩余水头高度无影响。 因此在实际双排水盲沟设计中应首先明确水位降深范围,尽量减小降深对排水盲沟渗流的影响。其次,在确定了水位降深和最大剩余水头高度时,双排水盲沟的间距可适当增大,以减小工程投资。2.2 计算方法二
3 双排水盲沟渗流计算的有限元计算方法
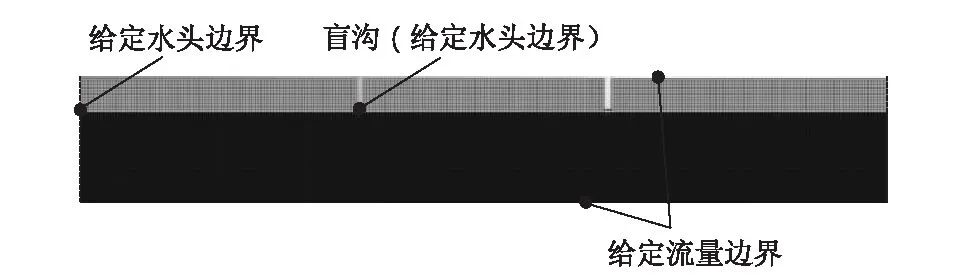
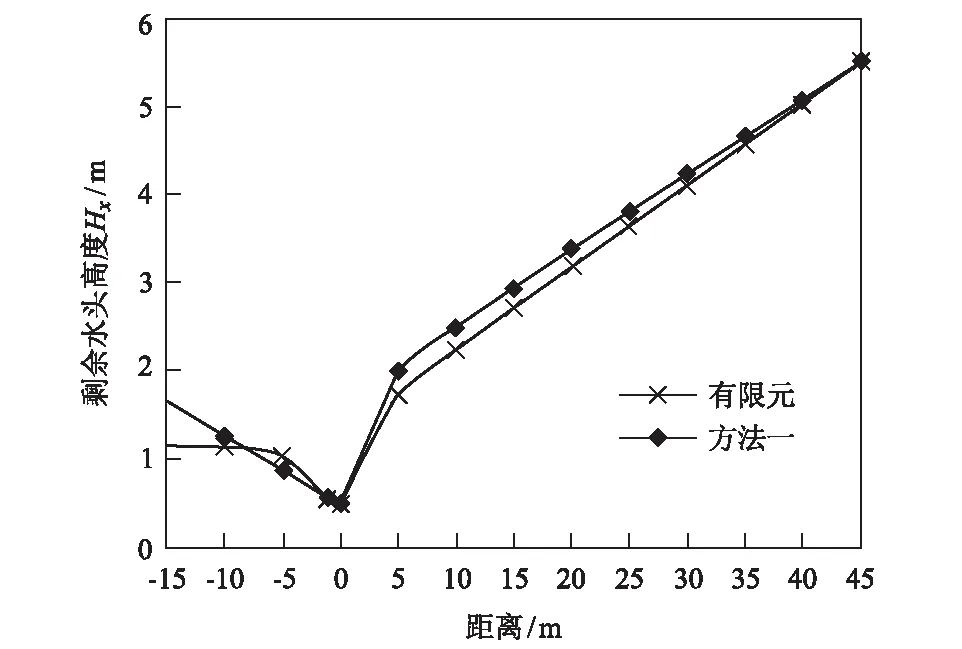
4 计算实例对比


5 双排水盲沟渗流影响因素分析
5.1 盲沟间距对双沟渗流计算结果的影响
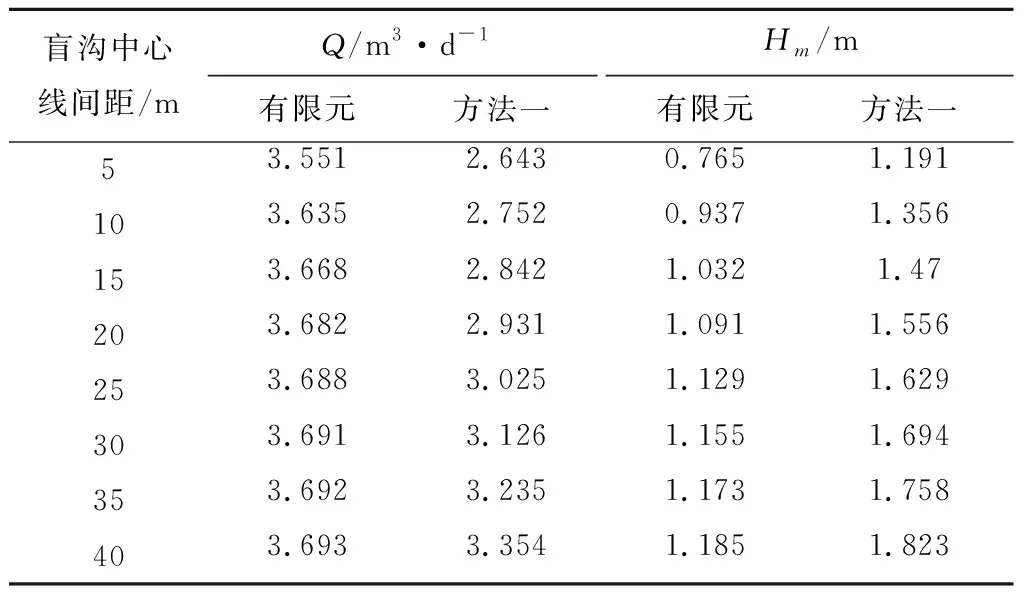
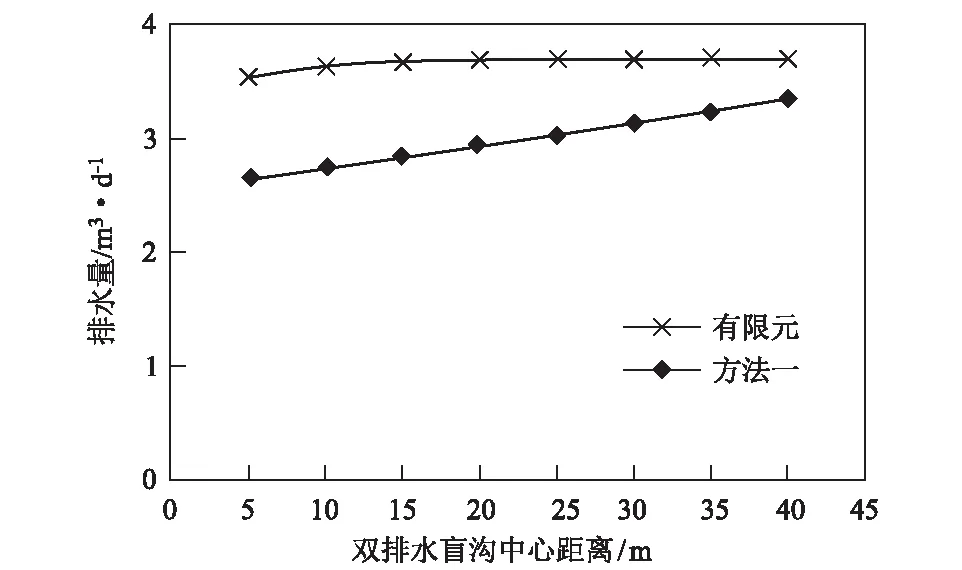
5.2 降深对双沟渗流计算结果的影响

5.3 渗透系数对双沟渗流计算结果的影响

6 结语
