一种识别谐波分量主瓣干扰的方法
2019-01-07,,
, ,
(上海电力学院 电气工程学院, 上海 200090)
近年来,越来越多的非线性负载接入电网,使得电网信号中存在大量谐波和间谐波,而谐波和间谐波的准确检测对谐波源的定位和谐波治理具有十分重要的意义[1]。
快速傅里叶变换(Fast Fourier Transform,FFT)是改进的离散傅里叶变换(Discrete Fourier Transform,DFT),能在计算机上实现高效运算,已成为目前最常用的谐波分析方法之一。由于实际情况下对信号的同步采样很难严格实现,所以频谱泄漏和栅栏效应难以避免。加窗能够抑制频谱泄漏,插值能够校正栅栏效应带来的误差,所以加窗插值FFT算法被广泛应用于谐波分析中[2-4]。此方法将信号在频域展开,搜索谱峰并利用主瓣内的谱线来校正谐波参数,在处理不含频率相近成分的信号时,通常具有较高的精度。旁瓣性能优良,窗函数能有效抑制主瓣所受泄漏的影响,但是旁瓣性能越好,窗函数的主瓣宽度往往越大,频率分辨率也就越低,在处理含有频率相近谐波和间谐波成分的信号时,频率相近分量的主瓣会相互干扰,这一现象影响了加窗插值FFT算法的精度。针对加窗插值FFT算法频谱分辨率不足的缺点,许多学者使用时域算法来处理间谐波信号。常用的时域算法有MUSIC 算法[5]、ESPRIT算法[6]和Prony算法[7]等。这些方法在理论上具有无限小的信号频率分辨率[8],可以分辨频率相近的谐波和间谐波,但是算法的稳定性和精度与信号中谐波和间谐波成分的个数有关,且计算速度较慢。
在进行谐波分析时,应优先采用精度和稳定性较高的加窗插值FFT算法;当信号中存在频率相近的谐波和间谐波成分时,再考虑使用时域算法来处理。因此,准确判断信号中频率相近的分量之间是否存在主瓣干扰就显得尤为重要。本文从理论上推导了主瓣内谱线的相位特性,以此为判据建立了主瓣干扰的判断方法,并利用仿真实验来验证该方法的有效性。结果表明,本文的方法能够准确判断主瓣干扰是否存在,进而判断信号是否含有频率相近的成分。
1 频率相近成分的频谱分析
当待测信号仅含有整数次谐波时,选用主瓣宽度适宜的窗函数并使用加窗FFT算法能够得到主瓣互相分离的频谱,谐波个数与主瓣数量一一对应。在这一情况下,插值算法能够得到精度很高的谐波参数。若信号中存在频率相近的谐波和间谐波分量,它们的主瓣会重叠,甚至会合为一个主瓣。
设信号表达式为
(1)
式中:A1,A2——两个分量的幅值;
f1,f2——两个数值接近的频率;
φ1,φ2——相位。
为此,通过信号加窗得到加窗信号,加窗信号的幅值谱如图1所示。
从图1可以看出,两个频率分量的主瓣由于位置过于接近而重叠在一起,这种现象被称为主瓣干扰。信号的真实频谱是两个分量的频谱矢量叠加的结果。在此幅值谱中仅有一个主瓣被呈现,若此时使用插值算法校正谐波的频率、幅值和相位参数,将会得到误差较大的参数。通常,信号中大部分分量的频率都有一定距离,它们对应的主瓣没有受到干扰,而只有个别谐波和间谐波分量的主瓣距离会太近而相互干扰。如果在加窗FFT得到的频谱基础上,增加一个判断主瓣干扰的步骤,根据主瓣干扰的判定结果采取不同的处理方式,将会得到更理想的谐波和间谐波参数的检测结果。
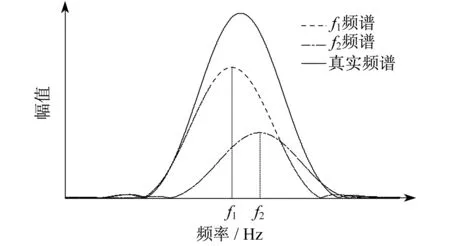
图1 加窗信号的幅值谱
2 主瓣干扰的判据
主瓣干扰发生时,主瓣内谱线相位将会明显改变,因此可以将主瓣内谱线的相位作为主瓣干扰的判据。余弦组合窗是目前最常用的一类窗函数,其时域通用表达式为
(2)
式中:M——窗函数的项数;M=0,1,2,…,M-1;
n——窗函数数据点数,n=1,2,3,…,N-1;
am——窗函数的系数。
式(2)所示余弦组合窗的频谱表达式为
(3)
式中:WR(k)——矩形窗的离散傅里叶变换。
(4)
将式(4)代入式(3)并简化得到
(5)
设W(k)的实数部分为
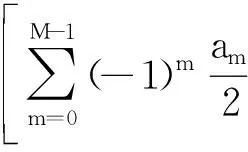
(6)
则式(5)变为
W(k)=F(k)·e-jkπ
(7)
F(k)的图像如图2所示。由图2可知,当-M
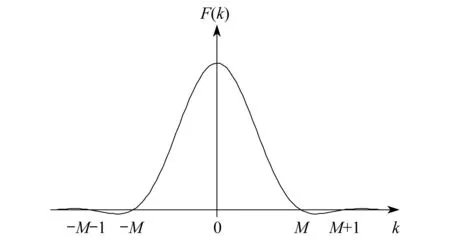
图2 函数F(k)的图像
设加窗信号为xw(n)=x(n)w(n),其离散傅里叶变换为Xw(k)。文献[3]指出,在计算第i项谐波参数时,可忽略负频率和频谱泄漏的影响,认为
(8)
式中:Ai,φi——第i项谐波的幅值和相位;
ki——第i项谐波的频率在DFT中的等效值。
设主瓣内相邻的两根谱线分别为第k1和(k1+1)根,忽略频谱泄漏的影响,两根谱线的值分别为
(9)
(10)
两根谱线的相位差为
arg[Xw(k1)]-arg[Xw(k1+1)]=
(11)
式(11)表明,在忽略频谱泄漏的情况下,主瓣内两根相邻谱线之间的相位相差π(或-π)。
本文选取靠近主瓣峰值的两根谱线,如图3所示,这是某单频信号的幅值谱。
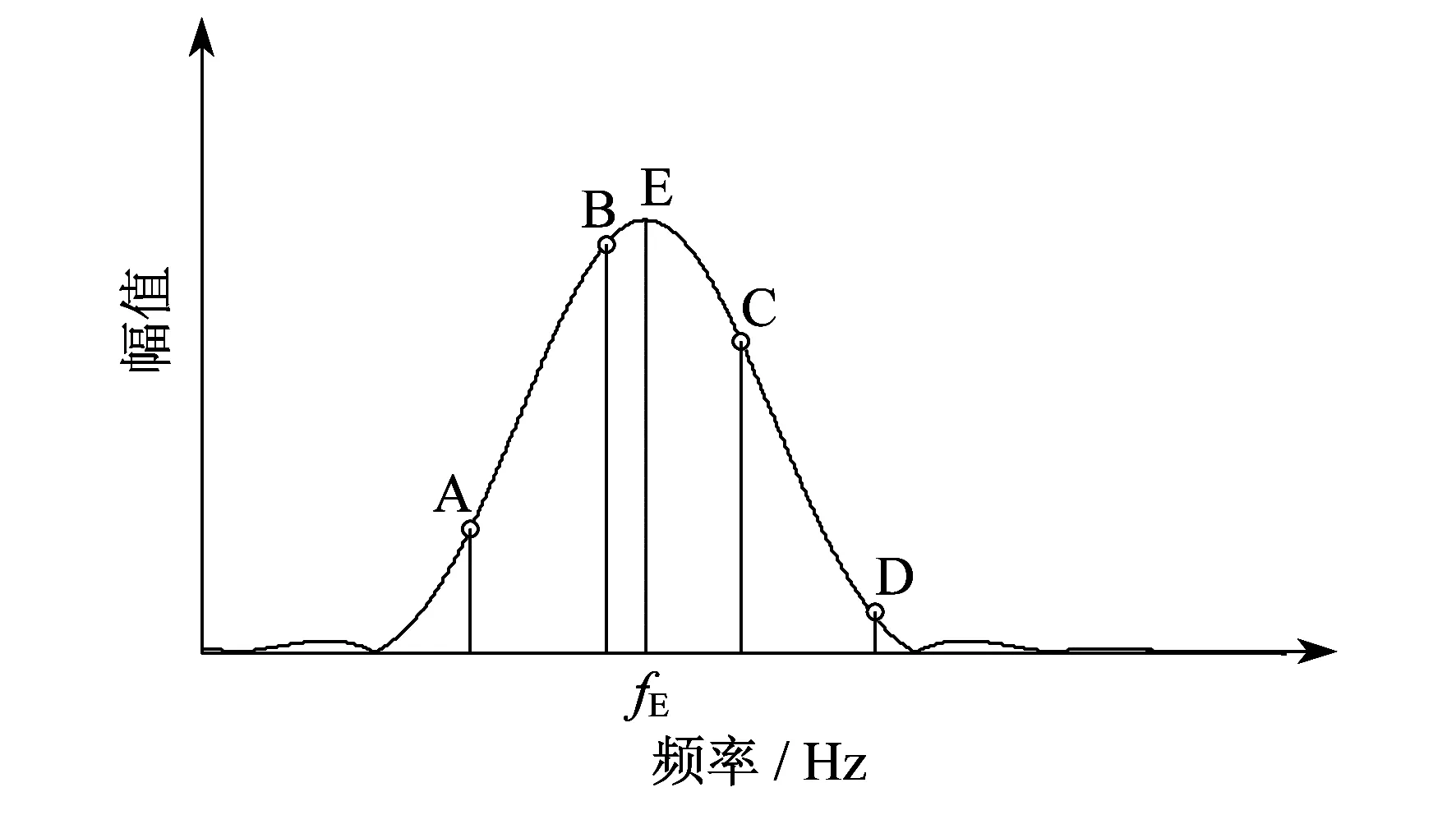
图3 单频信号谱线示意
图3中,fE为单频信号频谱中峰值处E点的频率;谱线B和谱线C为靠近主瓣峰值的两根谱线,即幅值最大的两根谱线。设φB和φC分别为这两根谱线的相位,其相位判别式为
Δφ=||φB-φC|-π|
(12)
在实际情况中,由于频谱泄漏的影响,Δφ通常不能严格等于零,所以只要Δφ小于一定阈值ε就可以认为主瓣干扰不存在,否则判定主瓣干扰存在。本文通过对典型谐波信号的频谱分析发现,ε的合理取值为10-5。
3 算例分析
在文献[3]给出的信号中加入靠近整数次谐波的间谐波分量,得到新的信号,信号表达式为
πfht+φh)
(13)
式中:h——谐波或间谐波成分的序号,h=1,2,3,…,12。
信号参数如表1所示。在这个信号中,基波、2次谐波和3次谐波附近都存在一个间谐波,如果直接使用加窗插值FFT算法进行处理,上述分量将难以被区分出来,计算结果误差会很大。为了避免这种情况,在计算信号参数前使用本文方法来处理待测信号。
设置采样频率为2 560 Hz,采样点数为512,窗函数为4项5阶Nuttall窗,对上述信号进行加窗FFT,得到加窗信号的频谱有9个主瓣,再对这9个主瓣依次进行主瓣干扰的判断,结果如表2所示。表2表明,本文方法能够准确判断主瓣干扰是否存在,同时可根据主瓣位置确定频率相近成分所在的频率范围。
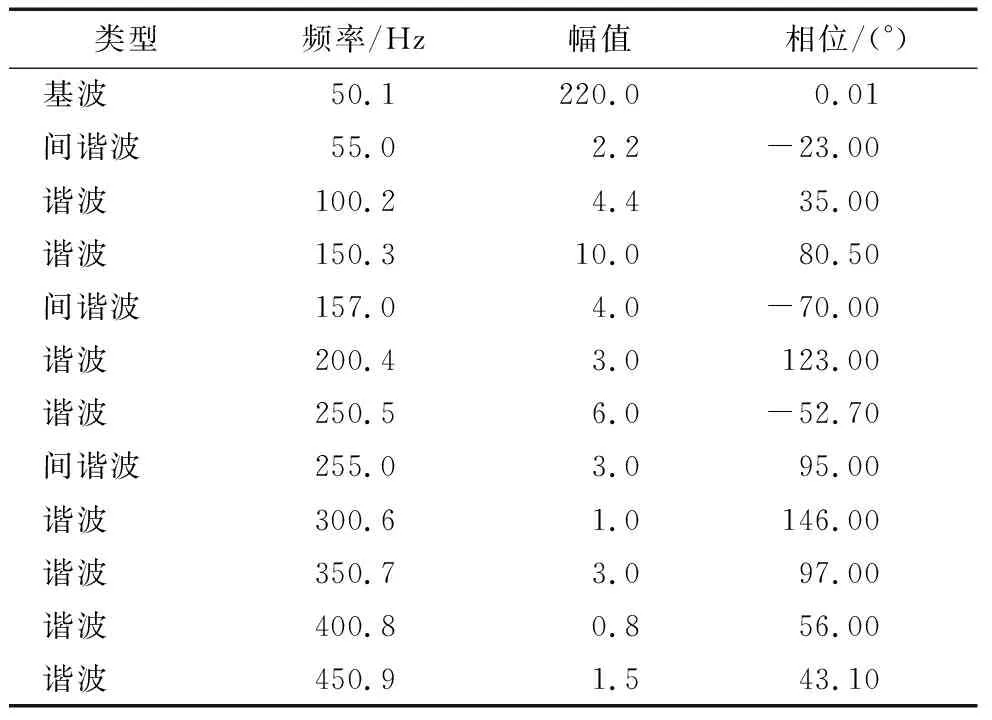
表1 信号参数
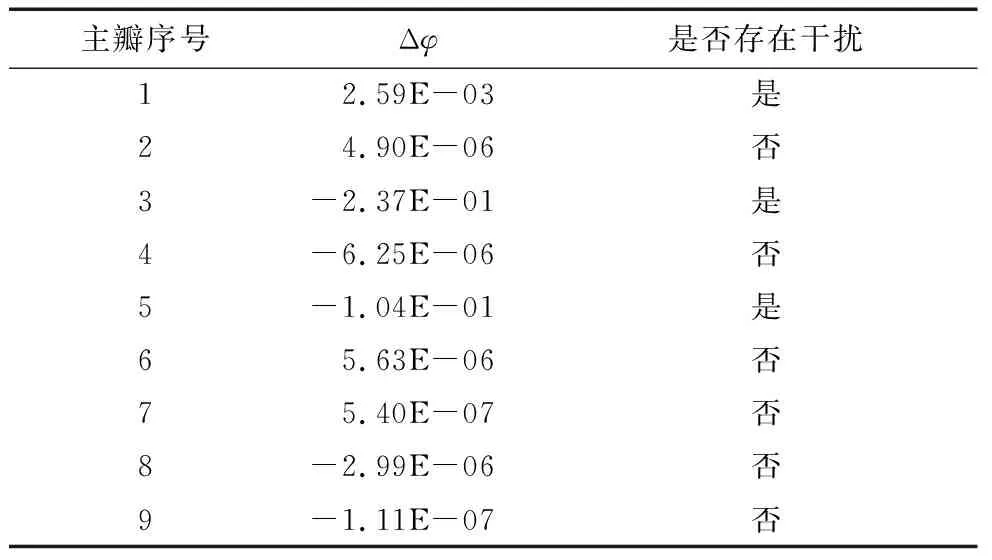
表2 主瓣干扰判定结果
4 结 语
本文分析了电网信号含有频率相近谐波和间谐波分量时频谱的特征,推导了主瓣内谱线相位公式,得出了主瓣内相邻谱线相位相差π(或-π)的结论,并以此为依据构建了主瓣干扰的判据。仿真结果表明,本文方法能够准确判断主瓣是否受到干扰,并且可以根据主瓣位置确定频率相近谐波和间谐波成分所在的频率范围,能为后续谐波和间谐波的检测提供帮助。
