一种多分支配电线路的故障定位方法

2019-01-07贾丽璇赵进全

吉林电力 2018年5期

王开，王军，常城，张晶，贾丽璇，赵进全

(1．延安供电局，陕西延安716000;2．西安交通大学，西安710049)

配电网结构复杂，规模庞大，故障率较高，据统计，配电网的故障占电力系统各种故障的80%以上。故障不仅影响用户的正常供电，还会破坏电力系统的安全运行，并造成较大的经济损失［1］，因此，配电线路故障后快速准确地故障定位，对及时排除故障，提高供电可靠性具有重要的意义。然而，由于配电线路线长、点多、面广，通道复杂，故障及其原因复杂多样，加之线路分支多，故障过渡电阻大，故障信号难以有效检测等，使得精确定位非常困难［2］。虽然目前有阻抗法、行波法等多种故障定位方法，但这些方法各有特点，实用性很不理想［3］，因此，人工巡线仍然是目前常用的方法，但巡线距离长，而且需要投入大量的人力、时间和物力，该方法已经远远不能满足实际要求了。研究一种快速准确的配电线路故障定位技术具有重要的现实意义［4-6］。本文基于输电线路分布参数模型，提出了一种多分支配电线路的故障定位方法。该方法由线路两个端点的电压、电流求得的故障点的电压具有唯一性，据此可求得故障点的位置，可推广到多分支配电线路的单相接地故障定位当中，仿真结果证明了本文方法的正确性与准确性，为配电线路的故障定位提供了理论依据。

1 基于分布参数的多分支配电线路故障定位方法

1．1 配电线路的故障定位原理

这里以平行双导体传输线为例，说明输电线路的故障定位方法，这种方法可以推广到多导体多分支配电线路的故障定位之中。

对于平行双导体传输线，其上的电压与电流满足频域方程，即:

式中:Z0=R0+jωL0、Y0=G0+jωC0分别为传输线单位长度的阻抗、导纳。

(1)式的解为:

式中:U=U(x=0)，I1=I(x=0);

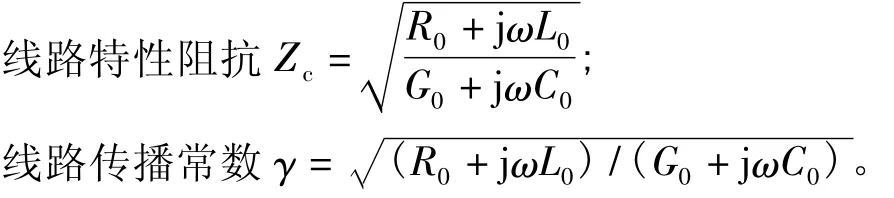
假定线路在F点发生单相接地短路故障，见图1。根据A点的电压、电流测试值，由(2)式得x点的电压为:

图1 线路故障示意图

根据B点的电压、电流测试值，由(3)式得x点的电压为:

式中:Ux为距A端x处的电压;UA、IA为线路A点的电压、电流测量值;UB、IB为线路B点的电压、电流测量值;l为线路总长度。

令

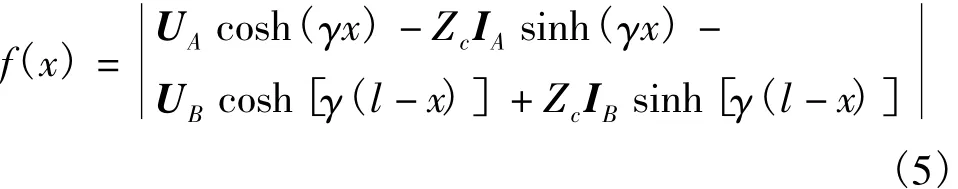
由以上求解过程可知，在已知线路参数的情况下，根据线路两端的电压、电流测量值即可获得故障点的位置。这种方法消除了过渡电阻的影响，具有高的定位精度。

1．2 多分支配电线路故障定位方法

对于多分支的配电线路，为了便于说明问题，这里以π型线路为例(见图2)，说明单相接地故障的定位方法。

图2 π型线路结构示意图

1．2．1 故障线路的判断

根据A、C端点的电压、电流测量值得到的M点的电压为UMA、UMC，根据B、D端点的电压、电流测量值得到的N点的电压为UND、UNB，由M点的电压、电流确定的N点的电压为UNM，由N点的电压、电流确定的M点的电压为UMN。

a．如果 UMA=UMC=UM，UNA=UND=UN，UNM=UN或者UMN=UM，则线路无故障。

b．如果 UMA=UMC=UM，UNM=UND=UN，UNM≠UN或者UMN≠UM，则故障发生在线路MN段。

c．如果 UMA=UMCUM，UNM=UND≠UNB，则故障发生在线路 BN段;如果 UMA=UMC=UM，UNM=UNB≠UND，则故障发生在线路DN段。

d．如果 UNB=UND=UN，UMN=UMA≠UMC，则故障发生在线路CM段;如果UNB=UND=UN，UMN=UMC≠UMA，则故障发生在线路AM段。

1．2．2 线路故障点的位置计算

a．如果故障发生在AM(CM)段，根据 C(A)端的电压、电流确定M点的电压、电流，再根据A(C)、M点的电压、电流确定故障点的位置;同理，如果故障发生在BN(DN)，根据D(B)端的电压、电流确定N点的电压、电流，再根据B(D)、N点的电压、电流确定故障点的位置;

b．如果故障发生在MN段，根据A(或C)端点的电压、电流确定M点的电压、电流，根据B(或D)端点的电压、电流确定N点的电压、电流，再根据M、N点的电压、电流确定故障点的位置。

2 算例

基于Matlab软件建立的多分支10 kV配电网单相接地故障模型见图3，其中lAM=lNB=lND=6 km，lMN=3 km，lMC=9 km，测试电源线电压380 V，线路正序参数 R1=0．17 Ω/km，L1=1．2 mH/km，C1=9．7 nF/km;零序参数 R0=0．23 Ω/km，L0=5．48 mH/km，C0=6 nF/km。

假设单相接地故障发生在线路AM上，故障点距离测量点A分别为1 km、3 km和5 km，过渡电阻分别为10 Ω、20 Ω 和 100 Ω，以实测距离与故障距离差值计算相对误差，仿真结果见表1。

虽然本文方法在理论上定位精度不受过渡电阻大小的影响，从表1可见，过渡电阻的改变仍然会导致误差的改变，同时故障距离对定位精度有较大的影响。主要原因为:当线路发生故障后，线路参数因过渡电阻发生了变化，而本文方法仍然使用线路原参数计算;数值计算误差;此外，线路的分支数、线路长度等对定位精度都有影响。