基于小波降噪的转动惯量测试仪周期计算改进算法

，， ， ，，

(1.陆军工程大学 石家庄校区装备模拟训练中心，石家庄 050003; 2.华阴兵器试验中心，陕西 华阴 714200)

0 引言

转动惯量是弹药的重要静态参数特征量之一。准确测量弹丸的转动惯量能够更好地为弹药试验提供判定数据，同时也可为弹道分析提供可靠的原始数据[1]。测量转动惯量的关键在于周期测量，周期测量的准确性将极大影响最终测试数据的准确性。在试验测试中，使用某型弹药转动惯量测试仪进行85mm样柱校准时，其测量数据比标准数据偏大0.83%，偏差值已经超出设备测试精度，也不能满足试验要求。经过对设备处理信号的测试，发现计算机接收到的电压序列包含大量噪声信号。这些噪声信号由数据采集卡特性以及测量电路、外界光源干扰产生，导致电压序列局部有剧烈抖动，引起周期测量出现不稳定现象，使得测量误差值偏大。

目前，转动惯量误差分析集中于周期测量、系统阻尼等产生的随机误差作用影响。李彤华等利用弹体转动惯量扭振方程推导出误差公式，得到空盘转动惯量、标准件转动惯量及被测件转动惯量对误差的影响[2]。黄德东等同样利用转动惯量扭振方程推导误差公式的方法，分析了周期测量误差、系统阻尼、空盘周期以及被测件与空盘共摆周期对测量精度的影响，并采用多次测量计算平均值的方法减小周期测量误差[3]。这些方法对各影响因素的随机误差进行分析，没有涉及转动惯量测试信号噪声所造成的周期测量系统误差，因此其方法不能应用于信号噪声所导致偏差问题的解决。

本文从弹药转动惯量测量原理进行研究，分析周期信号获取过程中的误差来源，探索出一种改进的减小误差的新方法，并对该方法进行实验验证，获得了较好的效果。

1 转动惯量及转动周期测量原理

转动惯量是刚体内各指点到旋转轴的距离平方与质点质量乘积的总和。弹丸转动惯量是弹丸结构特征量，对弹丸的初始扰动、飞行稳定性以及射击散步等有较大影响，也是进行弹道计算的关键参数之一。

弹丸转动惯量测量包括复摆法、三线摆法和扭摆法等，其中扭摆法的测试精度高,误差一般小于1%,是应用较为普遍的测量方式。扭摆法的测量原理如图1所示，当转动台偏离平衡位置一定角度后再释放时，根据刚体定轴转动定律有：

(1)

其中：J为转动台绕转轴的转动惯量，θ为转动平台偏离平衡位置的角度，α=c/J为空气阻力系数，k为扭杆的扭度系数。

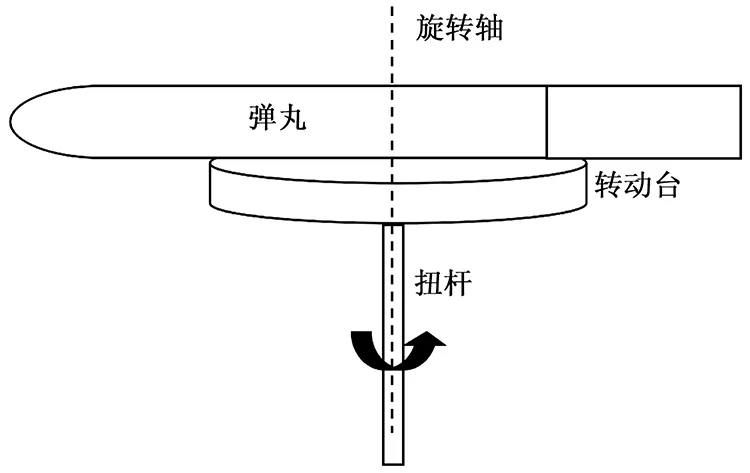
图1 转动惯量测试仪器结构示意图

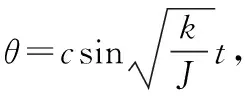
(2)

由式(2)可以看出，转动惯量和转动周期平方成正比，因此可以通过测量转动周期来计算转动惯量。由于扭杆扭度系数不易测量且会随着使用时间发生变化，因此一般使用转动惯量已知的标准样柱来消去该系数。分别测量空盘、标准样柱加空盘以及弹丸加空盘的转动周期数值，并代入式(2)，可以计算弹丸的转动惯量，公式为：

(3)

其中：T0为空盘的转动周期，Tb为标准样柱加空盘的转动周期，Td为弹丸加空盘的转动周期，Jb为标准样柱的转动惯量。由式(3)可知，转动周期的测量精度将直接影响到转动惯量的测量精度。

转动周期的测量，一般使用发光管与光敏器件配合，随着连接在转动台上的档杆周期性地遮挡发光管，测量电路将获得周期性的电压信号，测量原理如图2所示。

PCI数据采集卡每隔10 μs采集一次测量电路电压并实时传输到计算机，计算机软件对获取到的脉冲电压序列进行分析计算出转动周期值。

图2 转动惯量测试仪工作原理图

2 脉冲电压序列特性分析

使用测量设备进行实际测量，分别测量档杆完全挡住光敏器件时、档杆完全移开时以及空盘作周期摆动时计算机收到的脉冲电压序列，绘制图像如图3所示。

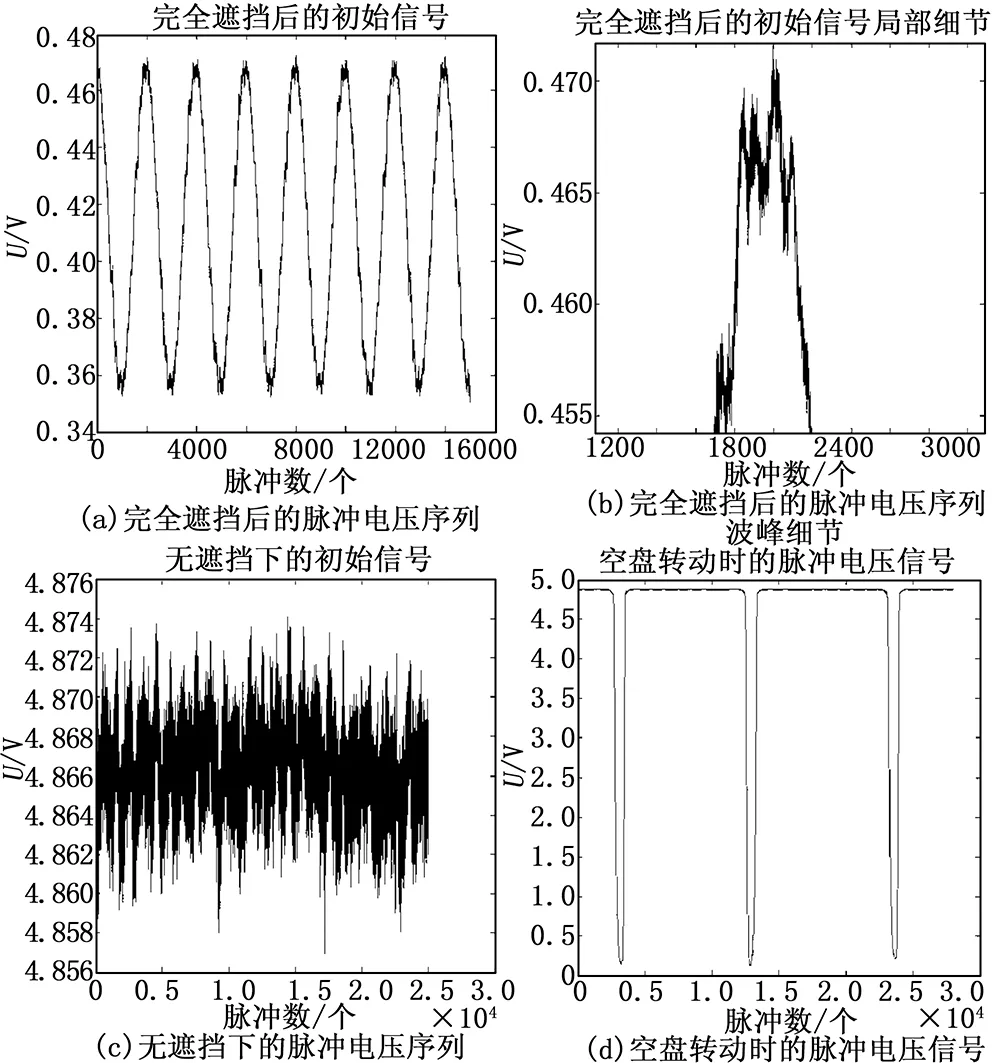
图3 脉冲电压序列图

图4 光电二极管的光电流—正电压特性曲线

由图3，可以得出以下结论：

1)由图4可知，在无光源照射的情况下(档杆完全遮挡光敏器件)，数据采集卡采集到的电压脉冲序列应为接近0的直线；而图3(a)表明，在实际情况下得到的电压脉冲序列为周期约20 ms(2000个脉冲)、上下限位约为0.47 V、0.35 V的正弦波信号；这是由数据采集卡的自身特性决定的；

2)图3(b)表明，脉冲序列不平滑，局部有剧烈抖动；

3)图3(c)表明，得到的脉冲序列包含大量噪声信号。

因此，计算周期的源数据—脉冲电压序列本身包含了数据采集卡自身特性以及测量电路、外界光源干扰带来的噪声信号。当噪声信号出现在周期计算截止电压处时，将导致测量得到的周期数值小于实际周期值，从而影响转动惯量的测量精度。

3 现有设备的周期计算方法分析

脉冲电压序列的波谷点代表档杆经过发光器件时遮挡程度最大的时刻，因此应计算相隔1个波谷的两个波谷点(相邻波谷代表档杆从相反方向经过发光器件)的脉冲个数，乘以采样间隔(10 μs)便可得到最精确的转动周期；而现有设备的周期计算方法里并未抑制脉冲电压信号中的噪声信号，因此脉冲电压序列局部存在剧烈抖动，很难准确找到波谷点，在此约束下，现有设备采用如图5所示的周期计算方法：

图5 现有设备的周期计算方法示意图

具体过程如下：

算法：现有设备周期计算方法

step 1：在脉冲电压序列里从大于截止电压处开始查找，直到找到连续N个(现有设备里N取5)小于截止电压(下降沿)的脉冲点，记录其序号i0；

step2：按照step1的方法依次找到上升沿、下降沿交替的靠近截止电压的脉冲点i1、i2、i3、i4、i5……i8等(则i1～i4之间为一个周期)。

step 3：获取2个周期值取平均数进行输出：(i8-i0)/2×10 μs。

如图6所示，当噪声信号叠加在正常信号上，且位于算法规定的截止电压处，则该方法记录的脉冲点序号小于实际序号，处理的得到的周期数值也小于实际周期，从而导致转动惯量计算出现较大误差。

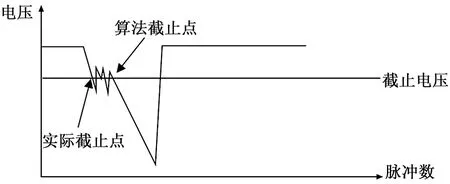
图6 可造成较大误差的脉冲电压序列示意图

4 采用降噪处理的改进周期计算方法

4.1 新方法的提出

以图3(d)的空盘脉冲电压序列为例，对其进行傅里叶变换，得到的图像如图7所示。

图7 空盘脉冲电压序列傅立叶变换对数图

由图7可以看出，脉冲电压序列信号包含高频噪声。去除信号中噪声常用的办法是将含噪声信号变换到频域后,然后设计相应的滤波器如低通、高通或者带通滤波器进行滤波处理。当干扰信号与有效信号频率相同或相近时，这一方法不能适用。从空盘脉冲电压序列傅立叶变换图可知，信号与噪声频率相近，不能采用滤波器进行滤波降噪。

小波分析是空间频率的局部化分析，通过对坐标轴的平移和伸缩，克服了窗口大小不随频率变换、缺乏离散正交基等缺点，达到了高频处时间细分、低频处频率细分，实现了对信号的精细分析[4]。由于具有多分辨率分析的特点，并可以聚焦到信号的任意细节进行多分辨的时频分析，小波分析被誉为“数学显微镜”。

小波降噪的方法包括模最大值检测法、屏蔽降噪法、阈值降噪法等。模极大值法去噪主要适用于信号中混有白噪声,且信号中含有较多奇异点的情况。1995年，Donoho等创造性地提出利用小波阈值降噪[5]，此后小波阈值降噪就成为对一维信号进行处理分析的重要方法。目前，阈值降噪方法是应用最多的降噪方法，而软阈值法是其中一种降噪方法。用软阈值法降噪得到的纯净信号是原始信号的最优估计,该估计信号的光滑性至少和原信号一样,而且不会产生附加振荡。乔玉坤等结合地磁数据规律以及匹配导航特点定小波分解层数方法，采用小波域软阈值降噪方法，有效降低了了地磁数据中的噪声[6]。刘军、陈光曦对声发射信号进行三层小波分解，对比选用软阈值降噪方法，显著提高了信号处理质量，保持了信号弱特征[7]。针对特定信号，采取改进阈值函数或自适应阈值函数等方法能够获得良好的降噪效果[8-11]。小波阈值降噪原理如下：

一个含有噪声的离散序列可以表示为如下形式，

di=f(ti)+σ·zi,i=1,2,…,n

(4)

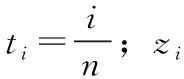
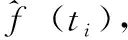
(5)

对di进行离散小波变换，可得

Yi=Yi(d)=Yi(f)+Yi(z)

(6)

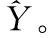
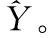
软阈值函数的表达式为：

ηT(Yi)=sgn(Yi)max(|Yi|-T,0)

(7)

其含义是将小波系数Yi的绝对值和阈值T进行比较，小于或等于阈值的系数变为0，大于阈值的系数变为其与阈值的差值，并保持符号不变。

硬阈值的表达式为：

(8)

即当Yi小于给定阈T时，将其置零；当Yi大于给定阈值T时，将之保留。

(9)

其中：ω-1为小波逆变换算子。

使用Matlab工具对信号进行小波降噪。仍以图3(d)的空盘脉冲电压序列为例，利用sym8小波对信号分解，在分解的第5层上，分别利用启发式SURE阈值选择算法、软SURE阈值选择算法、固定阈值选择算法对信号降噪，降噪后的结果如图8、图9所示。

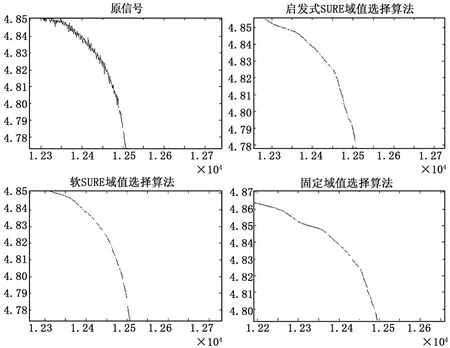
图8 不同小波降噪算法下的空盘脉冲电压序列细节比较(下降沿)

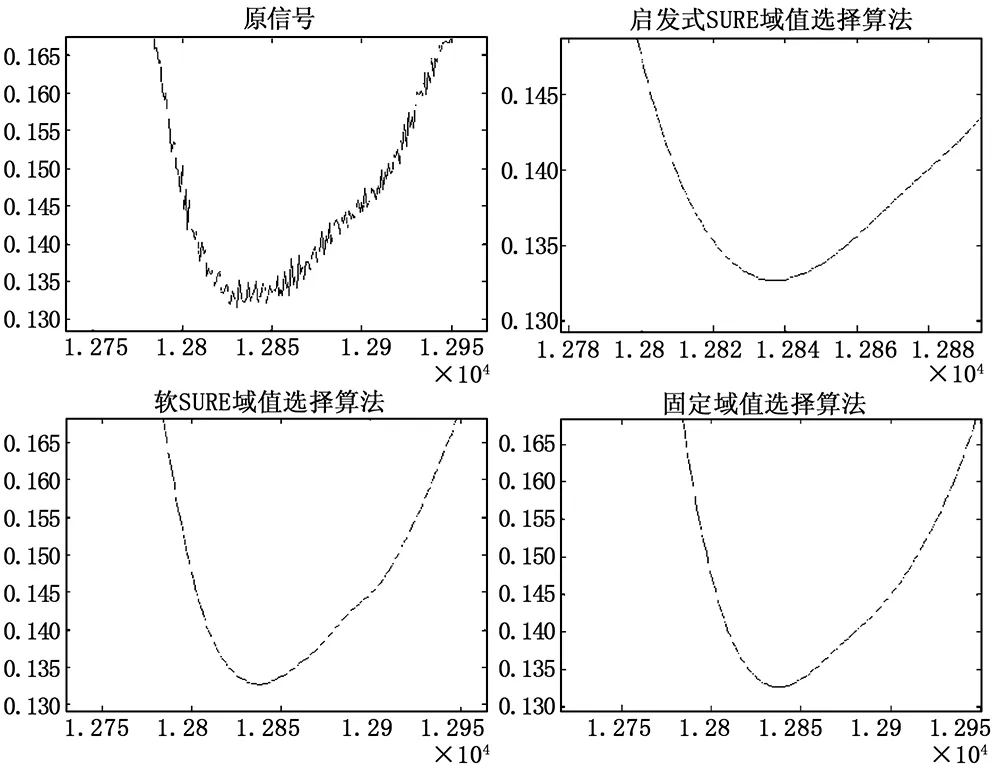
图9 不同小波降噪算法下的空盘脉冲电压序列细节比较(波谷)

图10 小波降噪后(启发式SURE域值选择算法)的空盘脉冲电压序列频谱对数图

由图8、图9可以看出，上述几种小波降噪方法都使得脉冲电压序列得到了平滑；对比图7、图10可以看出，小波降噪滤去了部分高频噪声。那么，根据第3节的分析，可以通过波谷脉冲点来计算转动周期。本文算法利用相邻两个波谷之间脉冲个数不会小于1000个(空盘1/2周期约为10000个)这一特点，设计周期计算算法如图11所示。

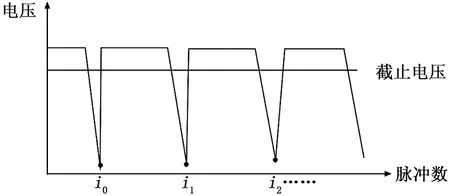
图11 采用降噪处理的改进周期计算示意图

具体过程如下：

算法：采用降噪处理的改进周期计算方法

step 1：对脉冲电压序列进行小波降噪；

step2：遍历脉冲电压序列，记录历史电压最大值，若当前脉冲点电压小于截止电压，则开始不断更新历史电压最小值，同时记录最小值对应的脉冲序号，直到当前脉冲点大于截止电压，清空最大值、最小值，记此过程中查找到的脉冲序号为i0；

step 3：重复step2，依次找到波谷脉冲点i0、i1、i2、i3、i4等(则i0～i2之间为一个周期)。

step 4：获取2个周期值取平均数进行输出：(i4-i0)/2×10 μs。

4.2 小波母函数的选取

在进行小波分析时，选择不同的小波母函数对同一个问题，也会产生不同的结果。小波母函数是多样化的,而且不同的小波母函数具有不同的对称性、消失矩等性质，因此其表达信号在时域和频域上局部特点的能力也不同。表达信号特点的能力越强,越有利于信号奇异点的检测。因此，小波母函数的选择非常重要。

除了比较小波函数本身的正交性、对称性等，还要注意具体应用环境的制约。MATLAB中提供7种离散小波系：haar小波系、db小波系、sym小波系、coif小波系、Bior小波系、rbio小波系、dmey小波系共50余种。为了寻求最优的小波母函数以便于更好地降噪，本文对实际试验获取的周期数据采用这50余种小波母函数进行降噪处理，并按式(10)计算降噪后的信噪比SNR。

(10)

其中：S′为含噪信号；S为纯净信号。

小波降噪后的信噪比越高，说明降噪效果越好。以85、100、105样柱作为被测物为例，表1给出了几种小波母函数处理被测物转动周期时的信噪比。本文选取并列出7种小波母函数进行计算，结果如表1所示。

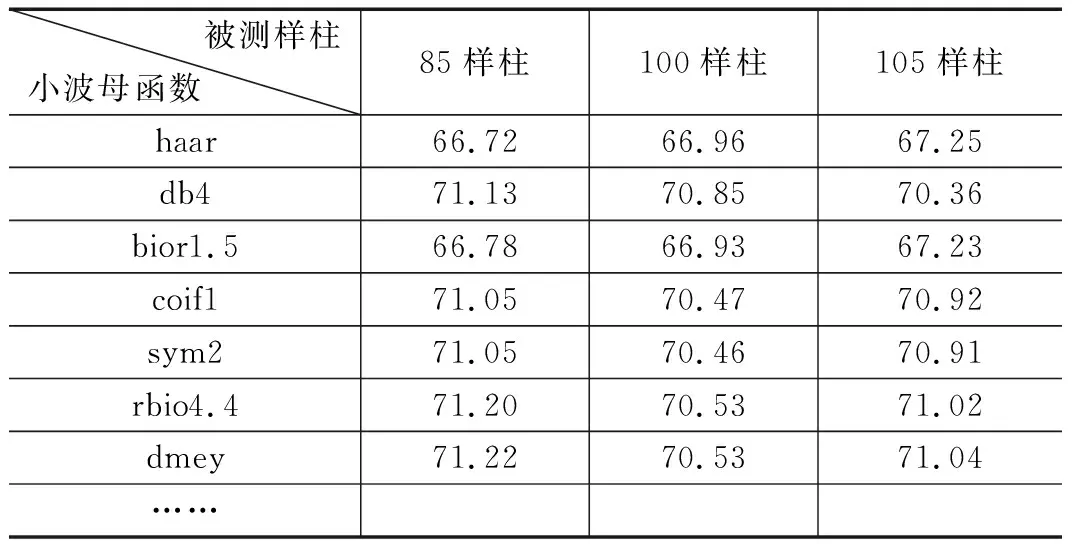
表1 多种小波母函数的信噪比对比

由表1可以看出，选择dmey小波母函数时的信噪比较高，说明其降噪效果较好，同时进行周期计算时也更为可靠。

4.3 新旧算法对比实验

使用多个不同样柱对新、旧两种周期计算方法进行对比，采用dmey小波母函数，对比结果如表2、表3所示。

由表2、表3可以看出，使用dmey小波母函数对测试信号进行处理，得到的周期方差值变小，测量数据结果一致性较好；从相对误差来看，使用新算法的相对误差减小，85 mm样柱相对误差由0.83%降至0.45%，122 mm样柱、152 mm样柱分别降低0.17%、0.16%，其他样柱误差下降幅度更大，因此通过小波降噪后计算得到的转动惯量计算值精度也较原有算法高。

表2 新、旧周期计算算法下的测量周期数据一致性对比

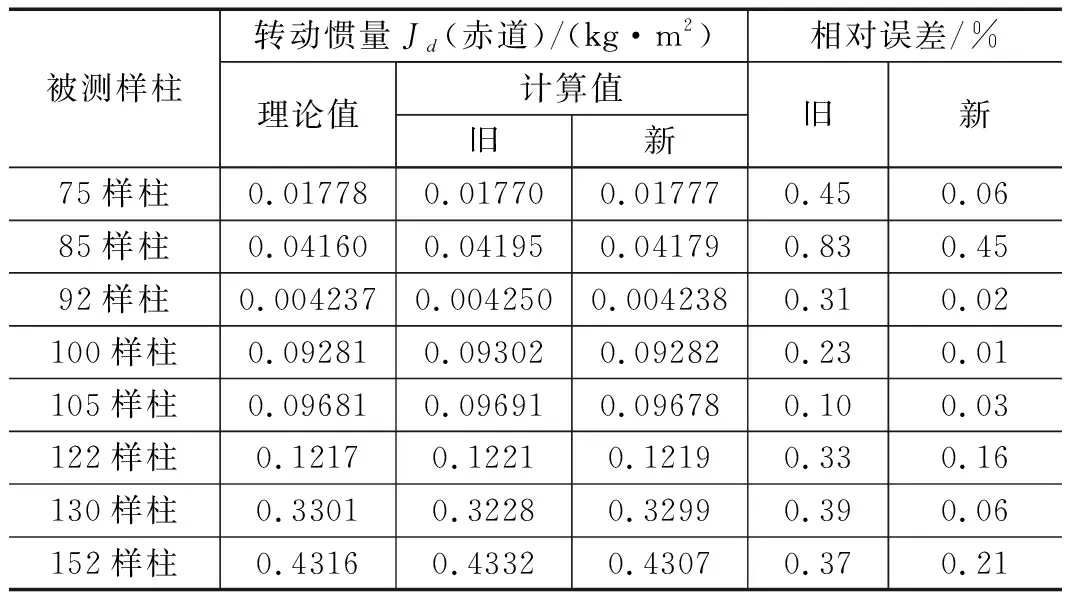
表3 新、旧周期计算算法下的转动惯量误差对比

5 结论

本文对转动惯量测量原理进行了分析，发现转动周期的测量会直接影响转动惯量测量的精度，而测量仪器在获取转动周期值时采用的原始脉冲电压序列数据包含了大量噪声信号，从而造成测量误差；通过小波降噪可以降低脉冲电压序列中的噪声信号，在此基础上提出了一种先降噪再采用波谷记数法的周期计算方法；通过实验确定了降噪效果最好的小波母函数，并对新、旧算法进行对比。实验结果表明，本文提出的采用降噪处理的改进周期计算方法，其数据一致性及精度均优于旧算法，可良好地应用于转动惯量测量领域。