自适应平方根球型无迹卡尔曼滤波算法
2019-01-07,,,,
, , , ,
(1.空军预警学院研究生大队, 湖北武汉 430019;2.空军预警学院, 湖北武汉 430019)
0 引言
目标跟踪是雷达数据处理的关键部分,然而很多情况下,观测数据和目标动态参数间的关系是非线性的。对于线性系统或非常接近线性的系统,一般能用线性的滤波方法给出满意的结果。然而,对于非线性的系统,用线性的估计方法往往得不到好的滤波效果,这时需要非线性的滤波方法。
目前,普遍应用的非线性滤波方法有扩展卡尔曼滤波(EKF)以及无迹卡尔曼滤波(UKF)。EKF是利用一阶泰勒展开的思想,将非线性系统近似线性化。因此,对于强非线性系统,EKF存在滤波性能极不稳定,甚至发散的问题。并且还要计算Jacobian矩阵及其幂,这在许多实际问题中很难求得[1]。而UKF是采用Unscented变换(UT),通过选取一组精确的sigma点来匹配非线性高斯系统状态的统计特性[2],进行非线性模型的状态与误差协方差的递推和更新。其不需要计算Jacobian矩阵,在相当运算量下具有估计精度和鲁棒性更高等优点[3]。然而,UKF需要用到对协方差矩阵的Cholesky分解,其要求协方差矩阵必须为对称正定矩阵。在滤波计算中随着迭代计算的累加,积累的舍入误差往往会破坏系统估计误差协方差矩阵的非负正定和对称性,导致滤波算法不稳定,甚至发生异常[1]。对于此,国内外的专家学者提出了许多改进算法。
文献[4]借助平方根卡尔曼滤波的思想,提出了一种平方根 UKF(Square-Root Unscented Kalman Filtering,SR-UKF)滤波方法,利用协方差平方根代替协方差参加递推运算,从而解决了由于协方差矩阵负定而不能求其平方根的问题,同时还提高了算法的计算精度。文献[5]提出的自适应平方根无迹卡尔曼滤波方法通过对传统的Sage-Husa自适应滤波算法进行改进,并与SRUKF算法相结合,能直接对非线性系统的状态方差阵和噪声方差阵的平方根进行递推与估算,确保状态和噪声方差阵的对称性和非负定性。文献[6]基于强跟踪滤波理论在改进的平方根UKF基础上引入多重自适应衰减因子调节协方差矩阵,提出了改进的强跟踪平方根UKF,使得滤波器具有自适应跟踪能力和克服系统模型不确定的鲁棒性。
本文在标准的平方根UKF算法上,通过改用球型无迹变换对权系数以及sigma点进行选取,改进平方根UKF中平方根矩阵的分解方法以及在预测误差协方差矩阵中引入了自适应衰减因子,设计了自适应平方根球型无迹卡尔曼滤波算法(ASRS-UKF)。将该算法同SR-UKF算法以及强跟踪UKF算法(Strong Tracking Square Root UKF,STSR-UKF)进行仿真对比,仿真结果证明了ASRS-UKF算法的有效性。
1 ASRS-UKF滤波算法
1.1 标准的平方根UKF滤波算法
设非线性系统的状态方程和量测方程:
(1)
式中:X为n×1维状态变量,f(X)为系统的非线性状态方程,Z为m×1维观测向量,h(X)为非线性的测量方程;wk为过程噪声,Vk为测量噪声,且wk及Vk均为均值为零协方差矩阵分别为Qk和Rk的高斯白噪声。
(2)
(3)
式中,chol为标准Matlab指令,表示Cholesky分解。
2) 计算选取sigma点:
(4)
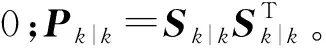
3) 时间更新:
(5)
(6)
(7)
(8)
式中,qr和cholupdate为标准的Matlab指令,分别表示QR分解和Cholesky分解一阶更新。
4) 量测更新:
(9)
(10)
(11)
(12)
(13)
5) 滤波结果更新:
(14)
(15)
U=KkSZ
(16)
Sk+1|k+1=cholupdate{Sk+1|k,U,-1}
(17)
其中,上述运用的权值计算表达式如下:
(18)
式中,β≥0为一个与状态的先验分布信息有关的参数,调节β可以提高协方差矩阵的精度。对于高斯分布来说,β=2是最优的。
1.2 算法的改进
1.2.1 球型无迹变换选取权系数以及sigma点
标准的平方根UKF算法中的sigma点和权系数分别由式(4)和式(18)来计算选取。系统、权值等参数种类多,需要精心调节各参数才能获得良好的滤波效果,调节过程较为繁琐,调节值还需要依靠部分经验确定;而且,其在无迹变换中,对于n维的状态向量需要2n个sigma点,这对于一般应用来说计算量太大。而球型无迹变换则只需要(n+2)个sigma点就能达到一般无迹变换的精度和数值稳定度,其对于权系数的选择也比较容易确定。
1) 权系数的选择:
W0∈[0,1)
(19)
(20)
式中,Wi(i=0,1,2,…,n+1)表示均值以及协方差加权的权值,而且W0一般取为0。
2) 计算sigma点,平方根形式的球型无迹变换sigma点计算如下:
(21)
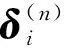
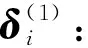
(22)
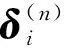
(23)
1.2.2 平方根矩阵的分解改进
在标准的平方根UKF算法中对于求向前一步预测的估计协方差平方根Sk+1|k由式(7)与式(8)给出,但按式(8)实际的可表达为
(24)
cholupdate要求式(24)的右边必须是正定的,因此运用cholupdate更新协方差矩阵要求比较高。
事实上根据向前一步预测的估计协方差矩阵计算公式:
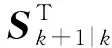
(26)
实际上进一步可令
rT=Sk+1|k
(27)
又由式(25)得
(28)
则由式(26)~式(28)可直接推得到Sk+1|k的更新方程如下:
(29)
(30)
同理对于式(11)和式(12)的量测估计协方差的平方根矩阵更新方程可以改为如下:
(31)
(32)
另外,在标准的平方根UKF滤波算法中对于状态误差协方差矩阵的更新按式(16)、式(17)可实际表示为
(33)
这要求式(33)的右边必须是正定的,但是在计算过程中,等式的右边由于含有相减的项,对舍入误差十分敏感,很容易因为舍入误差的积累,使结果失去正定性。因此还需对状态估计协方差的平方根矩阵作如下修改:
根据协方差定义得
(34)
由式(15)代入式(34) 得
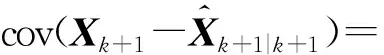
(35)
对于测量方程是在雷达测量球坐标系建立的,但是可以采用修正无偏转换到直角坐标系中,以位置分量来表示观测量,则可以得到伪观测方程为
(36)
(37)
把式(37)代入式(35)得(其中E为单位矩阵)
Pk+1|k+1=
(38)
Pk+1|k+1=
(39)
因此可以根据式(29)和式(30)的处理方法来得到改进的更新状态估计协方差的平方根矩阵:
(40)
(41)
下面将上述改进后的公式计算量与原公式计算量进行对比。对于一个x×y(x≥y)的矩阵[7],qr分解的计算复杂度为O(xy2),cholupdate更新的计算复杂度为O(2xy2),矩阵转置的计算复杂度为O(xlgx),矩阵乘法的计算复杂度为O(xy2)。因此式(7)、式(8)、式(11)、式(12)、式(16)及式(17)的计算复杂度分别为O(3n3),O(2n3),O(2nm2+m3),O(2m3),O(nm2),O(2n3);式(29)、式(30)、式(31)、式(32)、式(40)及式(41)的计算复杂度分别为O(3n3+n2),O(nlgn),O(2nm2+m2+m3),O(mlgm),O(3n3+2nm2),O(nlgn)。综上,原算法的计算复杂度为O(7n3+3nm2+3m3);改进后的算法复杂度为O(6n3+4nm2+m2+m3+mlgm+2nlgn)。一般情况下,状态参量的维数n大于观测量的维数m,因此,改进后的算法复杂度小于原算法。
1.2.3 引入自适应因子
对于滤波器,自适应算法的引入将有效改善其对不确定系统的跟踪性能。根据文献[6]可得,采用多重次自适应调节因子矩阵Dk+1调节状态误差一步预测协方差阵Pk+1|k可以达到良好的自适应调节效果,其具体形式如下:
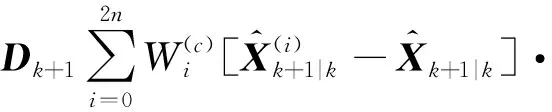
(42)
式中,多重次自适应调节因子的计算如下:
(43)
(44)
(45)
(46)
(47)
(48)
式中:Nii,Hii以及Jii分别表示矩阵N,H,J的第i行第i列的元素;m为量测向量的维数;Fk+1为状态方程的jacobian矩阵;ωk+1为残差,η为遗忘因子,取值在0~1之间,通常取为0.95。
则计算出自适应因子矩阵后,对于式(29)、式(30)的向前一步预测估计协方差平方根矩阵更新方程可以改为
(49)
(50)
2 雷达观测量转换
由上可得,雷达的非线性测量方程需要线性转化以简化运算,这可以通过雷达的观测量转换,用转化后的间接观测量(伪观测量)来替代实际的观测量来实现。
以雷达所在位置为原点,在纵平面上,目标位置信息主要由观测距离r以及俯仰角θ来表征,其中观测距离标准差为σr,俯仰角标准差为σθ,则对应的协方差矩阵为
(51)
目标的位置矢量与观测距离r、俯仰角θ有如下关系:
(52)
将位置x,y作为间接观测量来代替实际观测量r和θ,可得伪观测方程为
(53)
此时,还需要对观测协方差矩阵进行转换,根据协方差传播理论可得
(54)
(55)
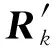
(56)
3 仿真及分析
3.1 仿真条件设置
设空中一目标以如下的运动方程运动:
(57)
式中:ax与ay分别为目标的横纵向加速度;ρ0=1.225 0 kg/m3为海平面的空气密度,ha=6 700为空气密度和高度之间的关系常量,g=9.8 m/s2为重力加速度,k=1为弹道系数。
设置目标与雷达站初始横向距离x(0)=0 m,初始高度y(0)=50 000 m,初始横向速度vx(0)=100 m/s,初始纵向速度vy(0)=200 m/s,仿真时长为500 s,目标运动轨迹如图1所示。
为了验证本文提出的ASRS-UKF滤波算法的有效性,分别将ASRS-UKF算法、SR-UKF滤波算法以及STSR-UKF算法对上述轨迹进行跟踪滤波。

(58)
式中,
(59)
上式的离散化形式可以简化为
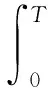
(60)
3.2 跟踪结果及分析
跟踪采样周期为0.1 s,测距精度为100 m,测角精度为0.001 5 rad,进行100次蒙特卡洛,得到的3种算法跟踪结果如图2~图5所示。
由图3得,在横向位置上,3种滤波算法的跟踪精度都表现不错,但是还是ASRS-UKF算法精度最高,其次是STSR-UKF算法,最差的是SR-UKF算法;在收敛速度上差距较明显,其中ASRS-UKF算法收敛速度最快(在10 s左右的位置),其次是STSR-UKF算法(在25 s左右的位置),最慢的是SR-UKF算法(在50 s左右的位置)。然而,在纵向位置上,ASRS-UKF算法则表现出了优越的性能,在收敛速度、跟踪精度以及稳定度上都明显要好于前两者,最差的是无自适应能力的SR-UKF算法。结合图2可以发现,在横向位置上目标轨迹较平缓,机动性较小,系统模型可以更好地匹配,因此3种滤波算法都表现不错;而在纵向位置上,目标轨迹变化较大,机动性较强,因此无自适应能力的SR-UKF算法无法稳定跟踪。
由图5可以看出,在横向速度上,3种滤波算法的跟踪情况都表现不错,其中跟踪精度上STSR-UKF算法略微优于ASRS-UKF算法和SR-UKF算法;但是在收敛速度上,ASRS-UKF算法则表现最快(在10 s左右的位置),其次是STSR-UKF算法(在25 s左右的位置),最慢的是SR-UKF算法(在45 s左右的位置)。在纵向速度上,ASRS-UKF算法在收敛速度、跟踪精度以及稳定度上要好于前两种,明显好于SR-UKF算法,STSR-UKF算法也有不俗的表现。结合图4可以发现,在横向速度上目标表现为匀加速运动,机动性较小,系统模型可以更好地匹配,因此3种滤波算法都表现不错;而在纵向位置上,目标的运动方程复杂,机动性较强,系统模型难以很好的匹配,因此SR-UKF算法跟踪性能最差。
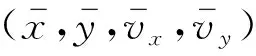
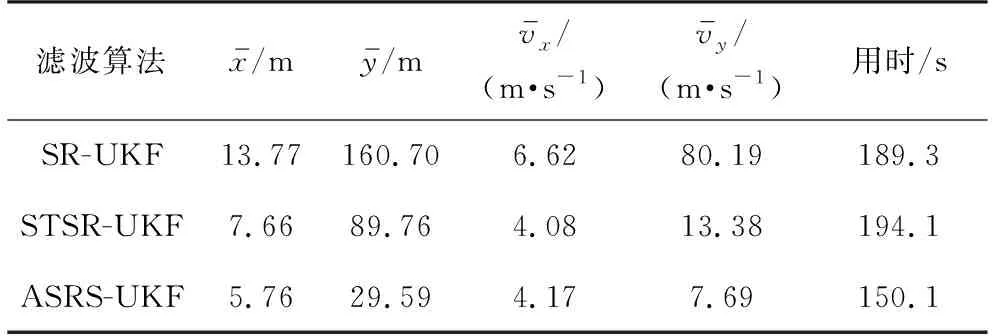
表1 各算法的总体跟踪性能比较
综上可得,本文的ASRS-UKF算法无论在计算速度、滤波精度、收敛速度以及稳定性都要好于SR-UKF算法和STSR-UKF算法,仿真结果验证了算法的有效性。
4 结束语
本文通过在标准的平方根UKF算法上,首先改用了球型不敏变换对权系数以及sigma点进行选取,其次改进了平方根UKF中平方根矩阵的分解方法,以及在预测误差协方差矩阵中引入了自适应衰减因子,设计了自适应平方根球型无迹卡尔曼滤波算法(ASRS-UKF)。最后,通过将该算法同SR-UKF算法以及STSR-UKF算法进行仿真对比,仿真结果表明,ASRS-UKF算法在减少计算量加快计算速度的同时还提高了滤波精度、收敛速度以及稳定性,而且对于目标机动性强、系统模型匹配不佳的情况下,仍具有良好的跟踪性能。
