Theoretical Investigations on the Structural and Electronic Properties of WO3Polymorphs①
2019-01-05JINHuZHOUHeGenZHANGYongFn
JIN Hu ZHOU He-Gen ZHANG Yong-Fn
Theoretical Investigations on the Structural and Electronic Properties of WO3Polymorphs①
JIN Huaa, b②ZHOU He-GenaZHANG Yong-Fanc, d②
a(336000)b(336000)c(350116)d(350002)
The structural characteristic and electronic properties of seven WO3bulk poly- morphs have been studied by first-principles density functional theory (DFT) calculations. Our calculation results indicate that according to the energy of WO3per unit, the stability of different WO3systems reduces in turn in the following order: monoclinic WO3, orthorhombic WO3, tetragonal WO3, triclinic WO3, hexagonal WO3and cubic WO3. And when the unit cell is distorted from the cubic framework, the alternatively long and shortW–O bonds are formed, implying an improvement of bonding-antibonding splitting associated with the interactions between W and O atoms. The deformation of the WO6octahedron enhances the stability of the system to some extent though the energy difference between various WO3phases is small (< 0.1 eV/per WO3unit).Besides, the band gap tends to enlarge accompanied with the symmetry decrease of WO3bulk. According to the band structures, the minimum band gaps for those WO3polymorphs are direct at thepoint except for the simple cubic and hexagonal structures. In addition, for all the WO3phases, the compositions of the valance band maximum (VBM) and conduction band minimum (CBM) are the same, which are relative to the O 2and W 5orbitals, respectively.
tungsten trioxide, band structure, electronic properties, DFT;
1 INTRODUCTION
WO3crystal is originated from the perovskite ABO3structure, and the basic building block of WO3bulk is a simple cubic perovskite-type unit with W atom occupying the center of an oxygen octahedron, and the octahedron is corner-sharing with another one. The distortions of the WO6octahedron and/or the displacement of W atom away from the center of the oxygen octahedra result in various deviations from the simple cubic WO3structure, giving rise to a group of low symmetric structures. Structural analyses have revealed that bulk WO3exhibits a series of polymorphs, and accompanied with the temperature increasing from 100 to 1,000 K. There are at least five different WO3crystalline phases, including-monoclinic (low temperature, LT), triclinic,-monoclinic (room temperature, RT), orthorhombic, and tetragonal phase. In terms of geometric feature, some previous reports mainly focus on individual WO3polymorphs or the phase transformation. For example, Corà.[6]calculated the geometric configurations of the simple cubic and tetragonal WO3, and found that the energy of WO3formula unit for cubic phase is 0.8 eV higher than that for the tetragonal one, owing to the elongating of W–O covalent bond. Experimen- tally, Vogt.[7]investigated the high-temperature phases (orthorhombic-WO3and tetragonal-WO3) of WO3with the help of high-resolution neutron powder diffraction. Their results further confirmed that the temperature-induced phase transitions in WO3can be rationalized according to the changes in the tilt direction of WO6octahedron and/or off- center displacements of the tungsten cations. Recently, Hamdi and co-workers[8]have inspected about five WO3crystal structures via a first-prin- ciples study. They took the phonon dispersion curves of a hypothetical cubic WO3as reference, and attributed the structural deformation of other WO3phases to their intrinsic cubic phonon instabilities.
On the other hand, the structural distortion has a major impact on the electronic properties. Early in 1983, Bullett[9]calculated the electronic structures of the cubic, monoclinic and orthorhombic WO3. His result indicated that detailed crystallographic arran- gement determines rather sensitively the size of the energy gap, involving an increase from 1.6 eV in the perovskite-like cubic structure to 2.4 eV in the full monoclinic distorted configuration. Then Chatten and co-workers[10]illustrated that the electronic structure of WO3is critically dependent on the splitting of W–O bond along each direction. The increase of W–O bond in thedirection results in the enlargement of band gap, while the W–O bond splitting along thedirection has an opposite effect on the band gap. Besides, accompanied with the W–O bond splitting, the WO3system varies from ionized to covalent. Wang.[11]presented a relatively comprehensive report on multifarious WO3crystalline phases by using hybrid functional with a series of Hatree-Fock exchange-correlation functional. Their calculation further confirmed that the band gap is strongly dependent on the structure of WO3. Very recently, Ping.[12]compared the electronic properties of three WO3crystal struc- tures-tetragonal, cubic and orthorhombic WO3, and they pointed out that the phases of WO3either at high temperature or under pressure exhibit a higher valance band maximum and smaller electronic gaps than the room temperature monoclinic WO3, and possess better visible absorption efficiency. Moreover, the orthorhombic WO3has much improved carrier mobility for both electrons and holes with respect to that in the monoclinic phase.
Despite a large number of reports and wide applications on the semiconductor material of WO3in recent years, little attention has been paid to a comprehensive study on the WO3solid bulk that contains various WO3crystalline phases[13, 14]. Especially, hardly any study referred to the hexa- gonal WO3form. According to the literature reports, WO3with hexagonal structure is predicted to show a high activity for degrading pollution, splitting water, gas sensing, and so on[15, 16]. At present it is of great interest for the special open-tunnel structure, and with the development of experimental technology, the metastable hexagonal WO3has been synthesized successfully[17]. There have been some experimental researches on the hexagonal WO3bulk, while almost no report on the crystal structure of this phase in the theoretical aspect. Thus, it is desirable to carry out more work for a better understanding on the structural and electronic properties of WO3with different crystal phases. In this work, we have systematically investigated seven WO3polymorphs at different temperature by the first principles calculations based on the DFT. All the thermo- dynamic stability, structural and electronic properties have been discussed here; also the experimental values and results of other theoretical groups are given for comparisons. We hope that our work can provide a theoretical guideline for the corresponding experiments and the design of WO3-based semicon- ductor material.
2 COMPUTATIONAL DETAILS
The structural optimization calculations were performed by using the Viennasimulation package (VASP)[18, 19]. The generalized gradient approximation Perdew-Wang (PW91) exchange- correlation functional[20] with ultrasoft pseudo- potentials (US)[21, 22]was used to describe the interaction between the ion cores and valence electrons (Support Information), and the kinetic cut-off energy for the plane-wave expansion was set to 400 eV. For each WO3phase, the corresponding unit cell was fully optimized with respect to both atomic coordinates and cell parameters. In the calculations, the convergence energy threshold for self-consistent iteration was set at 10-4eV/atom, and the residual atomic forces were smaller than 0.02 eV/Å. According to the lattice parameters of each phase, different sizes of Monkhorst-Pack-point meshes[23] were used, and the convergence test was carried out to determine the number of-points. From Fig. 1, the total energy per WO3formula unit converges quickly with the increase of the size ofmesh except the cubic and tetragonal phases. Considering the computational efficiency, a (7×7×7), (7×7×3), (6×6×6), (5×5×5), (5×5×5), (5×5×5), (5×5×3)-mesh was adopted for the simple cubic, tetragonal, orthorhombic, room-temperature mono- clinic, low-temperature monoclinic, triclinic and hexagonal WO3bulk phase, respectively. Addi- tionally, de Wijs[24]have proved that a 4×4×4 and 2×2×2 mesh is sufficient for the simple cubic and monoclinic WO3cell, respectively.
It is well known that the pure DFT method usually underestimates the band gap value of the semicon- ductors, therefore further calculations by using Becke’s three-parameter hybrids functional (B3LYP) were performed to obtain a good prediction of band gap of WO3. In this stage, the linear combination of atomic orbital (LCAO) method was employed to obtain the information about the band structure and density of states (DOS) with the help of CRYSTAL program[6]. The basis sets proposed by Corà.[6]were adopted for the tungsten atoms and all-electron Gaussian-type basis set 8-411 for oxygen atoms. Our previous studies have demonstrated that this two- step procedure could produce reasonable results for the solid bulk[25, 26].
3 RESULTS AND DISCUSSION
3. 1 Structural and electronic properties of simple cubic WO3
As shown in Fig. 1, it is clear that the simple cubic phase is the most unstable structure among various WO3polymorphs. This is in accordance with the previous results reported by other studies based on the GGA functional[27]. Actually, due to the high energy of cubic WO3, this crystalline phase has not been observed in the experiment, or it converts into other structures with lower symmetry. However, previous experimental investigation shows that this cubic framework can exist stably in the intercalated material with high concentration of dopant because of the large stabilization obtained by the impure- ties[28]. In addition, Crichton and co-workers[29]have successfully obtained the ReO3-type cubic WO3polycrystalline powder. Thus it is necessary to investigate the geometry and electronic properties of WO3with simple cubic structure.
The cubic WO3can be considered as the initial framework of other distorted configurations, and Fig. 2a displays the structure of a (4 × 4 × 4) supercell of WO3that contains 256 atoms. In this structure, each W metal atom has an ideal octahedral environment that is constructed by six neighboring O atoms. The unit cell has only a single WO3formula unit, where three O atoms locate at (0, 0, 0), (0,/2,/2), and (/2, 0,/2) sites, while the W atom is at (0, 0,/2). The parameterdenotes the lattice constant with a value of 3.77 Å. During the geometric optimization, there is only a single degree of freedom for the cubic system, and only the lattice constant () is optimized. Some calculated results including the lattice constant, equilibrium volume, and band gap are listed in Table 1, and the values obtained by previous HF and standard DFT calculations are also given for comparison.

Table 1. Lattice Parameters (Å and °), Equilibrium Volume (Å3/cell), and Band Gap (eV) of the Simple Cubic WO3
aFor all the tables, D and ID represent for the direct and indirect band gaps, respectively.
bConfiguration optimization at the GGA level using VASP and electronic structure analysis using the B3LYP hybrid functional employing CRYSTAL
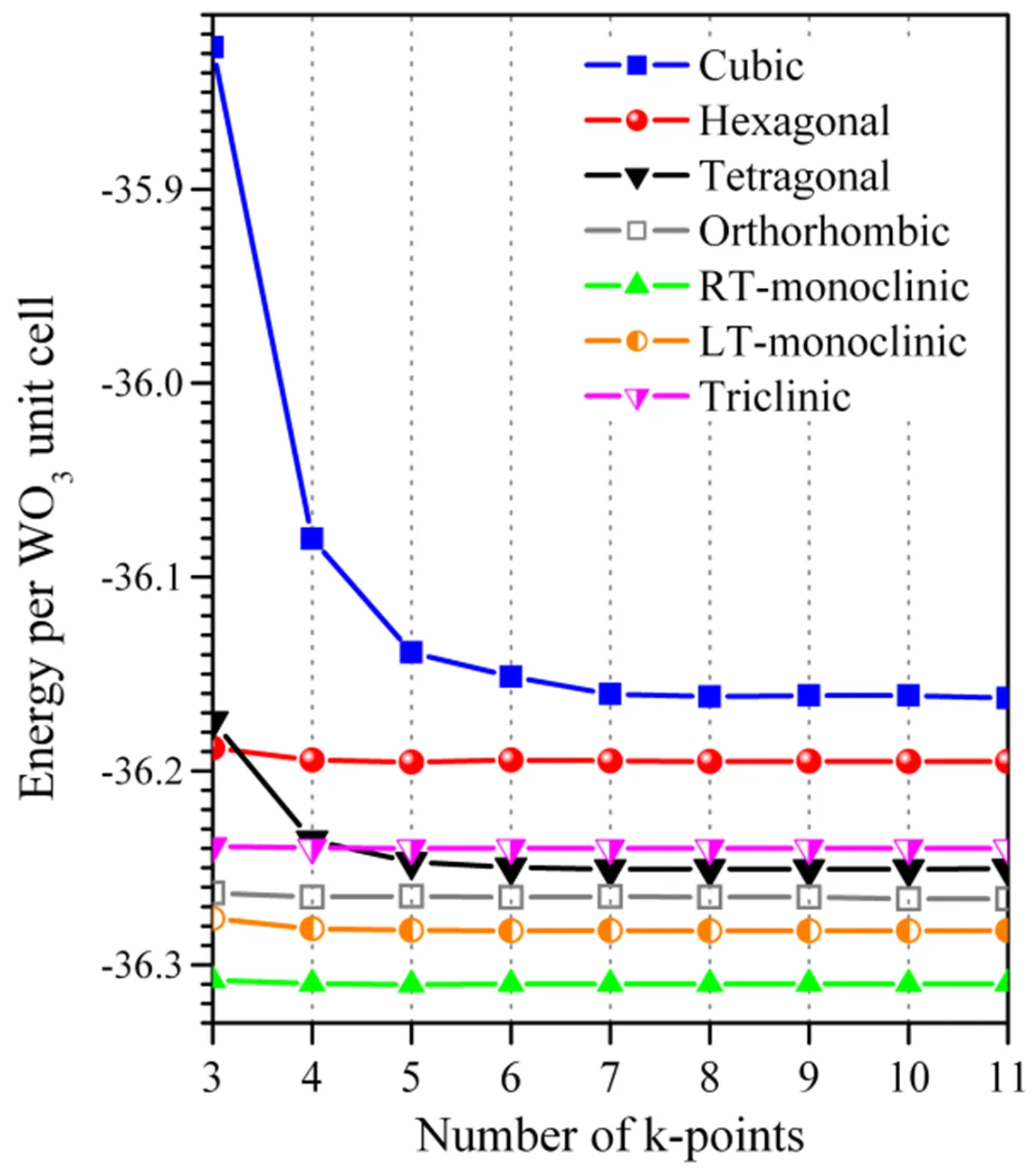
Fig. 1. Variation of energy per WO3unit cell as a function of the-points
Fig. 2. Structural model of (a) cubic, (b) RT-monoclinic, (c) LT-monoclinic, (d) orthorhombic, (e) tetragonal,(f) triclinic and (g) hexagonal WO3. The blue and red spheres represent W and O atoms, respectively. All the models shown contain 256 atoms, expect for the hexagonal phase, which contains 240 atoms
It can be seen that the lattice constant and equili- brium volume of unit cell predicted are severally 3.82 Å and 56.1 Å3, which agree quite well with the previous PW91 calculations, but still somewhat larger than the results obtained by HF method. Owing to the overestimation of lattice constants with the pure GGA functional, no matter what functional was employed, the calculated lattice constants and equilibrium volumes are larger than the experiment values, while if introducing some Hatree-Fock exchange correlation into the functional (namely HSE06), the corresponding results are closer to the experimental data. On the other hand, the calculated band gap is 1.42 eV (see Table 1), which is in agreement with the value reported by Wang[11]using HSE06 functional. Differently, the standard DFT method tends to underestimate the band gap of cubic WO3bulk with values smaller than 1.0 eV, while the HF method significantly overestimates the band gap, which is larger than 7 eV.
亚健康状态集中表现为心理、生理和社会适应三方面的症状.生理方面包括浑身乏力、容易疲倦、面容憔悴、脱发、颈肩僵硬、视力下降、腰酸背痛、心悸气短、胃闷不适、皮肤干燥、手足发凉、睡眠不良、多汗等;心理方面包括记忆力减退、早晨起床后不舒服、精力不集中、情绪不稳(包括情绪低落、紧张、烦躁、忧虑)、精神萎靡、多梦易惊等;社会适应方面包括个体间心理距离加大、人际关系不稳定、交往表面化、交往频率下降、物质化等.
Additionally, from the band structure displayed in Fig. 3a, we can see the minimum band gap of the cubic WO3corresponds to indirect transition, in which the VBM and CBM are located atandpoint, respectively. Besides, the top of valence band near the Fermi level in the~region is flat, which indicates that the effective mass for the holes is large. The analyses of DOS (see Fig. 3a) show that the top of valence band is mainly originated from the 2state of the O atom, while the hybridization of W 5and O 2orbitals is found in the regions about 1 eV below the Fermi level. Further, the conduction band is principally com- posed of the W 5states, and some O 2states can also be observed. The bandwidths of the valence and conduction band are 8 and 5 eV, respectively, and similar results have also been obtained by other previous studies[30].
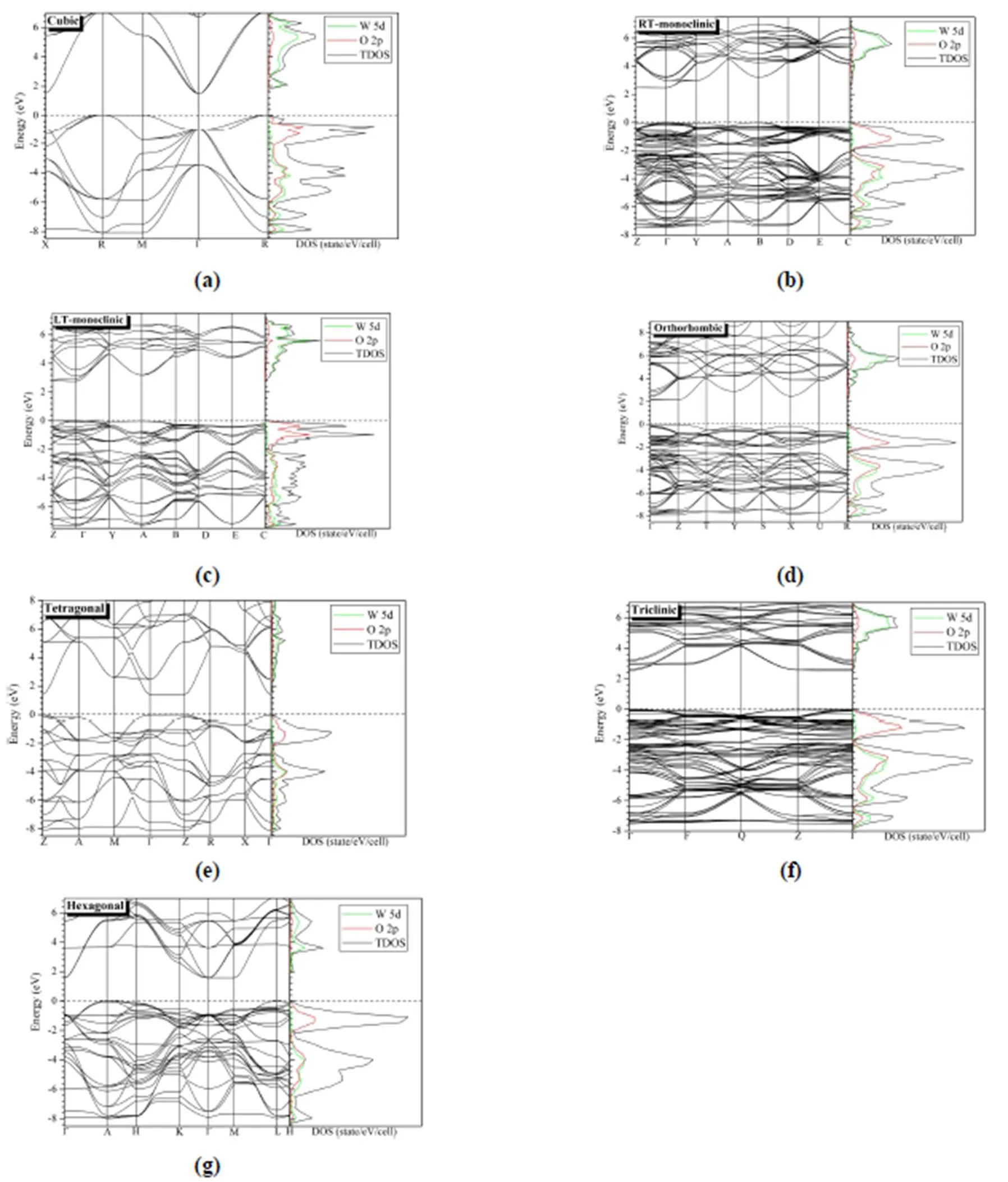
Fig. 3. Band structure and DOS of (a) cubic, (b) RT-monoclinic, (c) LT-monoclinic, (d) orthorhombic, (e) tetragonal, (f) triclinic, and (g) hexagonal WO3. Partial DOS plots are amplified several times for better visibility and all the energies are relative to the Fermi level
3. 2 Structural and electronic properties of RT-monoclinic WO3
The RT-monoclinic WO3(i. e.-WO3) with space group21/is a kind of distorted polymorph from the cubic structure, and is the most stable WO3crystalline phase. The experimental results show that the primitive unit cell of monoclinic phase has lattice parameters of= 7.31,= 7.54,= 7.69 Å, and= 90.9°, containing 8 W and 24 O atoms, that is, 8 WO3formula units. Fig. 2b shows a 2 × 2 × 2 supercell of the RT-monoclinic WO3. The whole WO3crystal structure can be also regarded as consisting of the repeat W–O–W like chains, where the chains are connected with each other by the W atom. Besides, along theandaxes, the W–O bonds exhibit alternatively long and short with bond lengths of 1.78 and 2.12 Å, respectively. Just because of this pseudo-low-dimensional structure, the monoclinic WO3exhibits many interesting pro- perties, such as superconductivity[31].

Table 2 shows the corresponding lattice para- meters of this WO3 polymorph. Similar to the cubic phase, no matter what functional is used, the calcu- lated crystal constants (i.e, the lattice parameters and equilibrium volume) are overestimated with respect to the experimental values, however, our research and the results of Wang et al.[11] obtained by HSE06 functional are in agreement with the experiment, with deviations of only 1.1% and 0.65%, respec- tively. The experimental study shows that the band gap of RT-monoclinic WO3 is in the range between 2.6 and 3.2 eV, so it is a kind of semiconductor material with an indirect band gap. Comparing the results obtained by different computational methods, all the band gap values for RT-monoclinic WO3 predicted by using the pure DFT method are less than 1.5 eV, indicating that the value of the band gap is underestimated obviously. While the hybrid DFT calculations exhibit relatively well estimation of the band gap to some extent. The values of band gap performed by HSE06, B3LYP functional and our method are severally 2.80, 3.13 and 2.47 eV, which are close to the experimental result.
According to the band structure shown in Fig. 3b, the CBM is located at the high-symmetricpoint and is twofold degenerate, and the VBM also lies at thepoint. Similar results are also obtained in previous HSE06 calculation, as well as the pure DFT method (Table 2). However, the experimental measurement indicated that the minimum band gap of monoclinic WO3phase corresponds to an indirect band, which is different from the theoretical predications. It must be noted that, the energy difference between the direct-transition fromtopoint and indirect-transition fromtopoint is very small (about 0.01 eV, see Fig. 3b). On the other hand, as we know the first-principles calculation simulates the substance at the ground state under the conditions of 0 K and zero pressure. Therefore, when the temperature rises from 0 K to room temperature, there may be part electrons filled at thepoint and then the energy band gap of the WO3crystalline phase could become indirect fromto. In addition, the top of the valence band and bottom of the conduction band are flat in the first Brillouin zone (BZ) fromto. This implies a high effective mass for the holes in VB and large effective masses in CB. This electronic characteristic has some interesting consequences in the behaviors of WO3crystal, such as the high prohibition of the conduc- tion in those directions. However, the energy bands at the Fermi level along other high symmetry lines are somewhat dispersive. The above simultaneous presences of both dispersive and localized bands around the Fermi energy level demonstrate the poten-tial of superconductivity for monoclinic WO3phase[32].
Considering the density of states (DOSs) of the RT-monoclinic phase as displayed in Fig. 3b, the valence band is mainly originated from the O 2state, while the conduction band consists of the 5orbital of the W atom, which is the same as the cubic structure. Moreover, the covalent interactions between W and O atoms can be observed in the energy region below –0.6 eV with respect to the Fermi level, especially in the region between –7.5 and –2.0 eV. The sharp rise of the valence band DOS at the Fermi level is due to the flat energy bands found in the band structure. Differently, the conduction bands near the Fermi energy level are more dispersive than the valence band (see Fig. 3b), which implies the DOS peak of the conduction band is less sharp contrast to the valence band. The bandwidths of VB and CB are about 7.5 and 4.5 eV, respectively.
3. 3 Structural and electronic properties of LT-monoclinic WO3
LT-monoclinic phase with space groupis ferro- electrically transformative structure of WO3, and can be denoted as-WO3. Its unit cell is composed of 4 W and 12 O atoms, i.e. four formula units of WO3. Fig. 2c shows a (2 × 4 × 2) supercell of-WO3. The lattice parameters obtained in the present work (= 5.28,= 5.13,= 7.64 Å, and= 92.3°) agree well with the experimental values, which can be confirmed in Table 3. Like other cases, there is a general trend that the PAW pseudo-potential brings a slight overestimation of the lattice constants. Thus the largest equilibrium volume for-WO3is obtained by using PAW pseudo-potential. In addition, compared with the experimental data, the results show that the hybrid HSE06 functional is better than the PW91 functional on the prediction of the WO3structure.
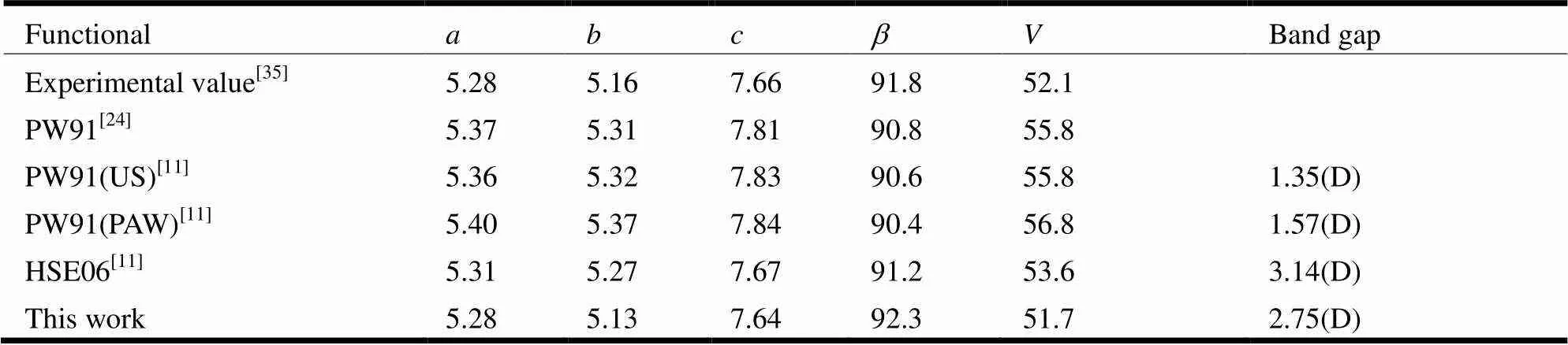
Table 3. Lattice Parameters (Å and °), Equilibrium Volume (Å3/cell), and Band Gap (eV) of the LT-Monoclinic WO3
As listed in Table 3, all the theoretical works indicate that the minimum band gap of-WO3corresponding to a direct transition occurred at thepoint. A value of 2.75 eV is obtained by using the B3LYP method, which is about 0.4 eV smaller than the result of HSE06 functional. The difference of the band gap between two monoclinic phases, namely the RT- and LT-monoclinic WO3, is not significant (2.75. 2.47 eV by B3LYP). Furthermore, the band structures of two monoclinic phases are also similar (see Fig. 3 b and 3 c). For example, in both phases the energy bands associated with VBM and CBM are quite flat in the~region. However, according to DOS plotted in Fig. 3c, the O 2state of LT-monoclinic phase tends to distribute in the region closer to the Fermi level with respect to RT phase.
3. 4 Structural and electronic properties of orthorhombic WO3
The orthorhombic phase with space groupis another distorted structure of WO3. The unit cell consists of eight WO3formula units and the lattice parameters are= 7.24,= 7.57,= 7.75 Å, and the corresponding cell volume is slightly larger than that of the RT-monoclinic WO3. Fig. 2d shows the structure of a (2 × 2 × 2) supercell of the orthor- hombic phase, in which the long and short alternate distributions of the W–O bonds can be observed in theanddirections, as a result of the off-center movement of W atoms.
The calculated lattice parameters and equilibrium volume of this crystalline phase are listed in Table 4. The cell parameters obtained in this work are= 7.48,= 7.62, and= 7.78 Å, respectively. Except an overestimation (about 0.24 Å) of the lattice parameter, our results are in coincidence with the experimental values. For other theoretical works, additional deviation (> 0.1 Å) of the lattice constantis also observed.

Table 4. Lattice Parameters (Å and °), Equilibrium Volume (Å3/cell), and Band Gap (eV) of the Orthorhombic WO3
With respect to electronic properties of the orthor- hombic phase, a direct minimum band gap is pre- dicted at thepoint, and the widths of the gap determined by HSE06 and B3LYP functionals are 2.57 and 2.13 eV, respectively (Fig. 3d). This value is larger than the cubic structure, but smaller than two monoclinic phases. The VBM of the orthorhom- bic phase mainly consists of the O 2orbital, and the CBM is dominated by the 5state of the W atom, which is the same as other WO3systems.
3. 5 Structural and electronic properties of tetragonal WO3
The tetragonal phase of bulk tungsten trioxide, which is also called as-WO3, is the most stable phase in the high temperature, and it is slightly distorted in contrast to the cubic structure. It has space group4/, and contains eight atoms (two WO3formula units per unit cell). Fig. 2e displays a (2 × 2 × 8) supercell of this crystalline phase. In the tetragonal WO3, there are two kinds of inequivalent oxygen atoms in the distorted WO6octahedron. Among them two oxygen atoms locate in the axial direction while the other four lie on the equatorialplane. The lengths of four W–O bonds in the equatorialplane are equal (1.91 Å); but in the axial direction the lengths of two W–O bonds are 1.78 and 2.12 Å, respectively, exhibiting an “anti-ferroelectric” characteristic with alternatively long and short W–O bonds. Owing to the limits of the experimental instrument, Kehl.[33]could not observe this long-short alternating arrangement of the W–O bond along theaxis. However, they found that the W atom departures from theplane by about 0.23 Å.
Table 5 shows the optimized lattice parameters for the tetragonal WO3polymorph. The lattice constants predicted here are= 5.32 and= 3.92 Å, which are consistent with the experimental values of 5.25 and 3.92 Å. Similar results are also obtained by employing PW91 and hybrid HSE06 functionals. Beyond that, it seems that PAW pseudo-potential tends to slightly overestimate the lattice constants and equilibrium volume compared to the US type pseudo-potential.
For the band gap of tetragonal WO3bulk, as expected, all the pure DFT calculations produce rather narrow band gaps with the value around 0.5 eV. When the hybrid B3LYP is employed, the band gap of the tetragonal WO3phase enlarges to 1.46 eV, which is close to result obtained by HSE06 func- tional (1.71 eV). Since the structural deformation is not obvious for the tetragonal phase, the band gap value is similar to the cubic one (1.46 eV. 1.42 eV by B3LYP method). Moreover, Corà and co- workers[6]have made a detailed comparison of the electronic structure between the cubic and tetragonal phases by usingHatree-Fock approach, and their results indicated that the difference in the W–O bonding between cubic and tetragonal phases results in only small difference for the band structure. In virtue of the band structure displayed in Fig. 3e, the VBM and CBM for the tetragonal WO3polymorph locate at theandpoint, respectively, while the energy difference betweenandpoints for the top of valence band is nearly the same (smaller than 0.01 eV), thus the tetragonal phase WO3exhibits a pseudo-direct band gap. The conduction and valence bands fromtoare quite flat, indicating that the effective mass of holes on the top of VB and that of electrons on the bottom of CB in~region are the largest. The VB width of tetragonal WO3is about 8 eV, which is close to the cubic structure but larger than that of the RT-monoclinic phase. Similar to the monoclinic and cubic structures, the VB is derived from the covalent interactions between W and O atoms, while the CB is dominated by the states of metal atom.
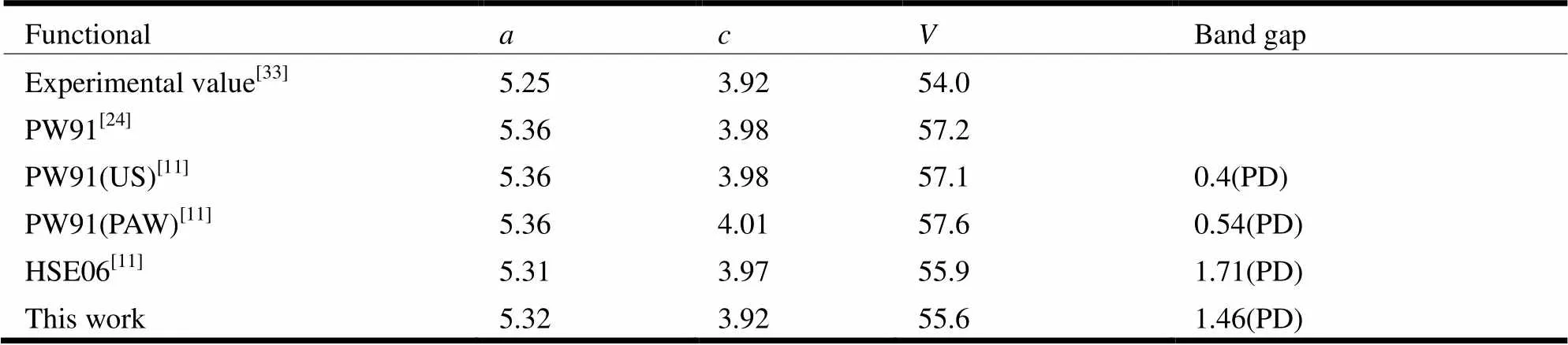
Table 5. Lattice Parameters (Å and °), Equilibrium Volume (Å3/cell), and Band Gap (eV) of the Tetragonal WO3
3. 6 Structural and electronic properties of triclinic WO3
The unit cell of the triclinic WO3phase (space group1) has 8 W and 24 O atoms, and Fig. 2f shows the structure of the corresponding (2 × 2 × 2) supercell. There is also a long-short arrangement of W–O bonds along three directions, indicating the deformation of WO3octahedra. Hence, the triclinic phase possesses the largest number of degree of freedom in various WO3structures. Table 6 lists the experimental and optimized crystal parameters of the triclinic phase. The lattice parameters obtained in this work are= 7.37,= 7.48,= 7.66 Å,= 88.6°,b= 91.1° and= 91.0°, respectively, which is accordant with the experimental values of 7.31, 7.53, 7.69, 88.8°, 90.9°, and 90.9°.
The band structure for the triclinic WO3phase is displayed in Fig. 3f. A direct minimum band gap is predicted at thepoint in our work, and the value of band gap is about 2.54 eV at the B3LYP level. As shown in Table 6, the PW91 functional with ultrasoft pseudo-potential and HSE06 functionals predict a direct band gap for the triclinic WO3. However, when PAW pseudo-potential was employed, an indirect minimum band gap is obtained. This dif- ference may be originated from that the energy bands near the VBM and CBM are very flat in the region betweento. Also, the same distributions of W 5and O 2states are observed as shown in Fig. 2f.
3. 7 Structural and electronic properties of hexagonal WO3
In addition to the aforementioned WO3crystal structures, hexagonal WO3(-WO3) is another pos- sibly stable phase for WO3although it can transform into a monoclinic structure when annealing WO3above 400°C. The hexagonal WO3is slightly more stable than the simple cubic structure (see Fig. 1) but much unstable compared with the other distorted WO3structures. The unit cell of hexagonal WO3with space group6/has three formula units of WO3, which is different from other WO3phases. Fig. 2g shows a (2 × 2 × 2) supercell with 240 atoms. Just like the tetragonal WO3structure, there are two types of oxygen atoms in the hexagonal WO3phase, that is to say, two axial and four equatorial oxygen atoms. Nonetheless, four W–O bonds in the equatorialplane are equal and the lengths of two bonds along theaxial are also the same, which is different from the arrangement of W–O bonds of the tetragonal WO3structure. As shown in Fig. 2g, the WO6octahedra of hexagonal WO3structure share their corners with each other, and special hexagonal and triclinic tunnels are formed along theaxis, which can be intercalation hosts to obtain hexagonal tungsten bronzes MWO3(M = Na+, K+, Li+,). Hexagonal WO3is predicted to be a promising material in electro-catalysis and negative electrodes of rechargeable lithium batteries[17].
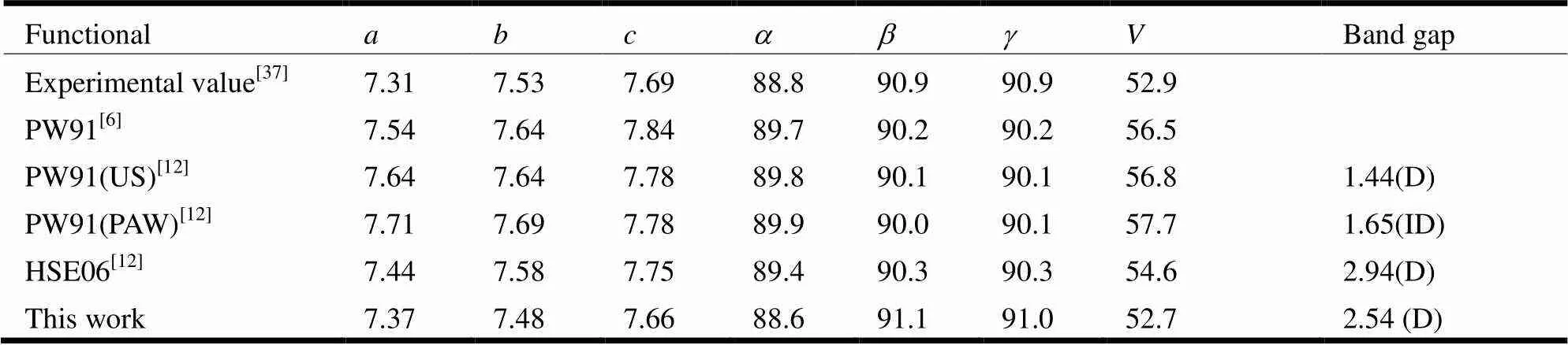
Table 6. Lattice Parameters (Å and °), Equilibrium Volume (Å3/cell), and Band Gap (eV) of the Triclinic WO3
The optimized cell parameters (= 7.40,= 3.82 Å) are also in line with the experimental values (= 7.30,= 3.90 Å). The minimum band gap of hexagonal WO3predicted by B3LYP functional is about 1.55 eV, and it is corresponding to an indirect transition from thetopoint. The band structure and DOSs of hexagonal WO3are shown in Fig. 3g. Further analyses indicate that the VBM is originated from the 2states of those oxygen atoms in the equatorialplane, while the CBM consists of the 5states of W atoms.
4 CONCLUSION
In this paper, we have systematically investigated the geometry and electronic properties of various phases of tungsten trioxides by using plane wave basis set combined with atomic orbital basis set. Our results of the structural optimizations agree well with the experimental measurements. Comparing the total energy of different WO3phases indicates the order of stability is RT-monoclinic > LT-mono- clinic > orthorhombic > tetragonal > triclinic > hexagonal > cubic. Examining the structures of RT-monoclinic and cubic phases, it seems that the distortion of WO6octahedron can enhance the stability of the system. In addition, the distortion of WO6octahedron also results in the long and short arrangements of W–O bonds, implying the improvement of bonding-antibonding splitting associated with the interactions between W and O atoms. Consequently, the band gap tends to be increased with reducing the symmetry of WO3bulk. By using hybrid B3LYP method, the band gaps of seven phases increase in the following sequence: simple cubic (1.42 eV) ~tetragonal (1.46 eV) ~ hexagonal (1.55 eV) < orthorhombic (2.13 eV) < RT-monoclinic (2.47 eV) ~ triclinic (2.54 eV) < LT-monoclinic (2.75 eV). Except for the simple cubic and hexagonal structures, the minimum band gaps are corresponding to the direct transitions at thepoint for other WO3phases. Although various W–O bond splitting occurs, the components of VBM and CBM are similar for all WO3phases, which are dominated by O 2and W 5states, respectively.
(1) Krasnov, Y. S.; Kolbasov, G. Y. Electrochromism and reversible changes in the position of fundamental absorption edge in cathodically deposited amorphous WO3.2004, 49, 2425-32433.
(2) Sallard, S.; Brezesinski, T.; Smarsly, B. M. Electrochromic stability of WO3thin films with nanometer-scale periodicity and varying degrees of crystallinity.2007, 111, 7200-7206.
(3) Xu, N.; Sun, M.; Cao, Y. W.; Yao, J. N.; Wang E. G. Influence of pH on structure and photochromic behavior of nanocrystalline WO3films.2000, 157, 81-84.
(4) Parvatikar, N.; Jain, S.; Khasim, S.; Revansiddappa, M.; Bhoraskar, S. V.; Prasad, M. V. N. A. Electrical and humidity sensing properties of polyaniline/WO3composites.2006, 114, 559-603.
(5) Yang, B.; Bames, P. R. F.; Zhang, Y. J. Tungsten trioxide films with controlled morphology and strong photocatalytic activity via a simple sol-gel route.2007, 118, 280-284.
(6) Corà, F.; Paterl, A.; Harrison, N. M.; Dovesi, R.; Catlow, C. R. A. AnHatree-Fock study of the cubic and tetragonal phases of bulk tungsten trioxide.. 1996, 118, 12174-12182.
(7) Vogt, T.; Woodward, P. M. Hunter, B. A. The high-temperature phases of WO3.1999, 144, 209-215.
(8) Hamdi, H.; Salje, E. K. H.; Ghosez, P.; Bousquet, E. First-principles reinvestigation of bulk WO3.2016, 94, 245124-11.
(9) Bullett, D. W. Bulk and surface electron states in WO3and tungsten bronzes.1983, 16, 2197-2207.
(10) Chatten, R.; Chadwick, A. V.; Rougier, A.; Lindan, P. J. D. The oxygen vacancy in crystal phases of WO3.2005, 109, 3146-3156.
(11) Wang, F. G.; Valentin, C. D.; Pacchioni, G. Electronic and structural properties of WO3: a systematic hybrid DFT study.2011, 115, 8345-8353.
(12) Ping, Y.; Galli, G. Optimizing the band edges of tungsten trioxide for water oxidation: a first-principle study.2014, 118, 6019-6028.
(13) Quiceno, J. C. A.; Dalpian, G. M.; Guillén, J. M. A systematic first-principles study of the tungsten trioxide polymorphs.2015, 252, 2290-2295.
(14) Heda, N. L.; Ahuja, B. L. Electronic properties and electron momentum density of monoclinic WO3.2013, 72, 49-53.
(15) Kong, Y. Q.; Sun, H. G.; Zhao, X.; Gao, B. Y.; Fan, W. L. Fabrication of hexagonal/cubic tungsten oxide homojunction with improved photocatalytic activity.. 2015, 505, 447-455.
(16) Tian, F. H.; Gong, C.; Peng, Y. H.; Xue, X. Y. H2sensing mechanism under different oxygen concentration on the hexagonal WO3(001) surface: a density functional theory study.2017, 244, 655-663.
(17) Salmaoui, S.; Sediri, F.; Gharbi, N.; Perruchot, C.; Aeiyach, S.; Rutkowska, I. A.; Kulesza, P. J.; Jouini, M. Hexagonal nanorods of tungsten trioxides: synthesis, structure, electrochemical properties and activity as supporting material in electrocatalysis.. 2011, 257, 8223-8229.
(18) Kresse, G.; Furthmüller, J. Efficient iterative schemes fortotal-energy calculations using a plane-wave basis set.1996, 54, 11169-11186.
(19) Kresse, G.; Furthmüller, J. Efficiency oftotal energy calculations for metals and semiconductors using a plane-wave basis set.1996, 6, 15-50.
(20) Perdew, J. P.; Chevary, J. A.; Vosko, S. H.; Jackson, K. A.; Pederson, M. R.; Singh, D. J.; Fiolhais, C. Atoms, molecules, solids and surfaces: applications of the generalized gradient approximation for exchange and correlation.1992, 46, 6671-6687.
(21) Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism.1990, 41, 7892-7895.
(22) Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements.1994, 6, 8245-8259.
(23) Monkhorst, H. J.; Pach, J. D. Special points for Brillouin-zone integrations.1976, 13, 5188-5192.
(24) de Wijs, G. A.; de Boer, P. K.; de Groot, R. A. Anomalous behavior of the semiconducting gap in WO3from first-principles calculations.1999, 59, 2684-2692.
(25) Zhang, Y. F.; Li, J. Q.; Liu, Z. F. Selective oxidation of the TiC(001) surface by O2: determined by the surface states.2004, 108, 17143-17152.
(26) Lin, W.; Zhang, Y. F.; Li, Y.; Ding, K. N.; Li, J. Q.; Xu, Y. J. Structural characterizations and electronic properties of Ti-doped SnO2(110) surface: a first-principles study.2006, 124, 054704-8.
(27) Migas, D. B.; Shaposhnikov, V. L.; Rodin, V. N.; Borisenko, V. E. Tungsten oxides. I. Effects of oxygen vacancies and doping on electronic and optical properties of different phases of WO3.2010, 108, 093713-093717.
(28) Balazsi, C.; Farkas-Jahnke, M.; Kotsis, I.; Petrás, L.; Pfeifer, J. The observation of cubic tungsten trioxide at high temperature dehydration of tungstic acid hydrate.2001, 141-142, 411-416.
(29) Crichton, W. A.; Bouvier, P.; Grzechnik, A. The first bulk synthesis of ReO3-type tungsten trioxide, WO3, from nanometric precursors.2003, 38, 289-296.
(30) Acens, A.; Hjelm, A.; Bellac, D. L.; Granqvist, C. G.; Barczynska, J.; Pentjuss, E.; Gabrusenoks, J.; Wills, J. M. Electrochromism of W-oxide-based thin films: recent advances.1996, 86-88, 943-948.
(31) Reich, S.; Leitus, G.; Tssaba, Y.; Levi, Y.; Sharoni, A.; Millo, O. Localized high-Tc superconductivity on the surface of Na-doped WO3.2000, 13, 855-861.
(32) Simon, A. Supraleitung und Chemie (Superconductivity and Chemistry).1997, 109, 1873-1891.
(33) Kehl, W. L.; Hay, R. G.; Wahl, D. J. The structure of tetragonal tungsten trioxide.. 1952, 23, 212-215.
(34) Crichton, W. A.; Bouvier, P.; Grzechnik, A. The first bulk synthesis of ReO3-type tungsten trioxide, WO3, from nanometric precursors.2003, 38, 289-296.
(35) Salje, E. K. H.; Rehmann, S.; Pobell, F.; Morris, D.; Knight, K. S.; Herrmannsdorfer, T.; Dove, M. T. Crystal structure and paramagnetic behaviour ofWO3-x.1997, 9, 6563-6577.
(36) Salje, E. The orthorhombic phase of WO3.1977, B33, 574-577.
(37) Woodward, P. M.; Sleight, A. W.; Vogt, T. Structure refinement of triclinic tungsten trioxide.1995, 56, 1305-1315.
10 April 2018;
22 August 2018
①This work was supported by the National Natural Science Foundation of China (21563030 and 21773030), the Jiangxi Provincial Department of Education Research Fund (12698), and the Independent Research Project of State Key Laboratory of Photocatalysis on Energy and Environment (2014A02)
Jin Hua, female, lecturer, doctor, majoring in computational chemistry. E-mail: jinhua_ycu@163.com; Zhang Yong-Fan, male, professor, doctor, majoring in theoretical and computational chemistry. E-mail: zhangyf@fzu.edu.cn
10.14102/j.cnki.0254-5861.2011-2040
猜你喜欢
杂志排行
结构化学的其它文章
- A Selective Luminescent Acetone Sensing Coordination Polymer Constructed from Zinc(II) Ions and Imidazolyl-bearing Ligands①
- Two Cd(II) Coordination Polymers Based on a Flexible Tricarboxylate Ligand: Syntheses, Structures, and Photoluminescence and Catalytic Properties①
- Blue-emissions Modulated by Packing Forces in Alkaline-earth Metal Organic Frameworks Based on Thiophene-2,5-dicarboxylic: Structures and Theoretical Calculations①
- Syntheses, Crystal Structures and DNA-binding Properties of Zn(II), Ni(II) and Co(II) Compounds Containing Thiazole Derivatives①
- A New Luminescent Cd(II) Coordination Polymer Constructed with 2-(Carboxymethoxy)benzoic Acid①
- Synthesis, Structure, and Optical Limiting Properties of an Axial Substituted Bis(8-oxide quinoline)zirconium Phthalocyanine①
