大尺度障碍物与泄爆面对天然气内爆炸的协同作用规律研究*

杨 凯，吕鹏飞，胡倩然，庞 磊

(1.北京石油化工学院 安全工程学院，北京 102617；2.北京市安全生产工程技术研究院，北京 102617)

0 引言

作为一种高效、清洁能源，天然气在城市居民生活中得到广泛应用。近年来，由于设备设施老化、违规使用等问题诱发的天然气爆炸事故已然成为城市居民生活中的典型事故类型之一。一般而言，民用建筑内天然气爆炸多始发在厨房，而厨房的门窗在爆炸过程中往往会成为具有一定开启压力的泄爆结构。同时，厨房内的橱柜、吊柜等物品很可能加剧爆炸瞬态流场的复杂性。气体爆炸属于非点源爆炸形式，爆炸过程受约束条件的影响极为显著。在典型的室内天然气爆炸事故中，具有一定开启压力的泄爆面与内置大尺度障碍物将共同作用于室内的爆炸流场[1]。

目前，关于泄爆结构对气体爆炸的影响规律方面已经取得了较多的研究成果。Bao，Qi，Fakandu，Guo等[2-5]分别借助不同形状、不同尺度的实验装置研究了开启压力、泄爆面积、相对位置等泄爆面属性对气体爆炸及泄爆的影响，但由于事故过程、工艺特点等方面的差异，并没有进一步考查内置障碍物的爆炸效应。

近年来，部分学者采用实验手段或数值方法对内置障碍物作用下气体爆炸及泄爆效应开展了大量研究，但民用建筑内的家具、电气设备等障碍物都是以大尺度为主，有关大尺度障碍物与泄爆面对受限空间内气体爆炸协同的研究还比较缺乏。由于天然气和液化石油气是2种主要的居民生活用气，因此很多文献[6-15]中主要利用这2种气体的主要成分甲烷或丙烷气体作为爆源开展研究。这些文献中泄爆面和障碍物特征是主要考察的2个参数。由于研究中爆炸腔室体积尺寸的分布范围较广，如Hall等[9]和Tomlin等[14]分别采用体积为0.000 625 m3和182.25 m3的爆炸腔室，研究了液化石油气和天然气的约束爆炸过程，使得各文献中泄爆面积和障碍物体积的差别较大，而约束泄爆过程具有尺度效应，小尺度泄爆实验结果不能直接用于指导民用建筑研究[1]。基于无量纲分析发现文献[6-15]中泄压比和障碍物面积阻塞率的分布范围较宽，分别为0.1～1和0%～70%。虽然这些文献考察了各种泄压比对泄爆过程的影响，但泄爆面的开启压力相对较低，均在数kPa范围内，而民用建筑房间玻璃的开启压力通常在数kPa到几十kPa之间。当房间泄压比在特定范围时，泄爆面开启压力增加将加剧室内爆炸超压强度。尽管Bao等[2]借助大尺度实验装置研究了泄爆面静开启压力对室内爆炸超压的影响，但并没有考虑室内障碍物的协同作用。障碍物的存在会增加室内湍流源，从而促进火焰速度和爆炸超压。虽然文献 [6-15]考察了圆柱、立方体、长方体等不同形状障碍物对约束泄爆过程的影响，但这些障碍物通常以小尺度细长形为主，并采用连续均匀方式布置，而民用建筑内的家具、电气设备等典型物品，特别是厨房内的障碍物的几何尺度通常较大[14]，障碍物布置较为紧凑。由此可见，目前同时涉及障碍物与泄爆面的有关研究主要针对小尺度连续障碍物，且泄爆面开启压力相对较低的情况，尚未关注房间内的大尺度障碍物与约束泄爆面之间的协同作用，而针对小尺度障碍物的研究对民用建筑天然气爆炸灾害研究的参考意义较为有限。

基于此，以典型民用厨房内天然气爆炸为例，研究了约束泄爆面与内置大尺度障碍物对爆炸动力学演化过程的协同作用机制，分析了泄爆面静开启压力和大尺度障碍物体积阻塞率对约束泄爆效应的影响，力求为此类事故的致因机理及事故防治提供科学依据。

1 数值方法

1.1 数值模型

基于计算流体动力学技术的气体爆炸动力学仿真软件AutoReaGas适用于气体爆炸及冲击动力学问题，且该软件的PRESSURFS边界条件可以根据实际情况对特定面结构设置特定的静开启压力，从而实现受限空间约束泄爆瞬态流场的求解，且该软件在求解气体爆炸泄压流场的可靠性已经在文献[16-17]中得到了验证。因此，本文采用该软件开展受限空间内预混气体约束爆炸研究。软件中假设可燃气体爆炸为单步不可逆化学反应，并采用有限体积法数值对包括质量守恒方程、动量守恒方程和能量守恒方程等一系列方程组进行求解来解决气体爆炸过程中的气体动力学行为[18]；通过k-ε模型来模拟气体爆炸中的湍流行为。

层流燃烧时的气体燃烧率Rfu=C1ρRmin，其中，C1为层流燃烧率模型常数，取系统默认值；ρ为密度，kg/m3；Rmin为燃料质量分数、氧气质量分数以及产物质量分数的最小值。

层流燃烧速度Sb可表示为：

Sb=Sl(1+FSRf)

(1)

式中：Sl为特定层流燃烧速度，m/s；Rf为球形火焰半径，m；FS为层流火焰加速系数，取值为0.15。

湍流燃烧时的气体燃烧率Rfu=Ctρ(St2/Γfu)Rmin；Ct为火焰速度常数，取值为40；ρ为密度，kg/m3；Γfu为湍流耗散系数；Rmin为燃料质量分数、氧气质量分数以及产物质量分数的最小值。

湍流燃烧速度St可以表示为：

St=1.8ut0.412·Lt0.196·Sl0.784·ν-0.196

(2)

式中：ut为湍流强度；Lt为特征长度尺寸，m；Sl为特定层流燃烧速度，m/s；v为未燃混合物的运动粘度，m2/s。

1.2 网格独立性验证

AutoReaGas采用8节点结构网格对空间离散，采用子网格技术描述小尺度实体对流场的作用[19]。为了考察网格尺寸对爆炸流场的精确捕捉的影响。选取尺寸为5 m×2 m×2.5 m房间作为研究对象。房间内无障碍物。在房间较小的一面竖直墙体上设有1个尺寸为0.5 m×0.5 m的泄爆面，其开启压力为60 kPa。在房间内充满浓度为9.5%且处于静止状态的甲烷/空气预混气体。点火源位于房间后壁中心处。针对该物理模型，分别采用0.1 m×0.1 m×0.1 m(M1)和0.05 m×0.05 m×0.05 m(M2)的2套尺寸对其进行网格划分，并对比分析了各算例的峰值超压。表1给出了2套网格的峰值超压对比数据。从表1中可以看出峰值超压的相对误差在10%以内，表明2种网格尺寸对本计算的影响较小，均可应用本计算，为了节约计算时间，采用尺寸为0.1 m的网格开展研究。

表1 峰值超压对比Table 1 Comparison of peak overpressure

1.3 数值模型的有效性验证

为了验证本文中数值模型的有效性，借助该数值模型对与本研究工况相类似的Bao等[2]开展的大尺度天然气爆炸实验过程进行数值模拟和对比分析。Bao等[2]采用2 m×2 m×3 m的大尺度实验装置开展了天然气爆炸与泄爆实验，并分析了6组不同静开启压力的泄爆面以及9组不同体积浓度的甲烷气体的泄爆效应，泄爆面面积为0.64 m2，点火源位于爆室中心位置，超压曲线取自爆室后壁几何中心位置的测点，爆室简化模型如图1所示。

图1 对比实验中[2]爆炸室简化模型Fig.1 Simplified model of explosion chamber in contrastive experiment[2]

在对应的数值模拟中，参照实验参数设置泄爆结构的开启压力和泄爆面积，其他墙壁均设置为刚性固壁边界。采用甲烷/空气预混气体作为爆源，其中甲烷体积浓度为9.5%。参照实验中的测试布置，将数值模拟中的测点布置在房间后壁几何中心，距离后壁0.1 m。点火源位于房间中心位置，点火时环境初始压力和初始温度分别设定为1.013 25×105Pa和300 K。基于实验工况，对泄爆面开启压力为1.5 ,12.1, 20.6, 31.4和62.7 kPa的5组泄爆工况分别进行了数值模拟。不同开启压力下数值模拟与实验所得的室内峰值超压如图2所示。

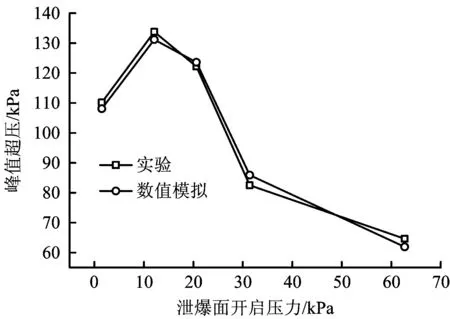
图2 实验与数值模拟结果中爆炸超压的对比Fig.2 Comparison of peak overpressure between numerical and experimental results

对比发现，实验和数值模拟的最大绝对误差为3.4 kPa，最大相对误差为4.2%。由于实验装置自身、传感器精度以及实验过程存在一定程度的不确定性，因此，其中的误差可能由实验测试误差与计算域离散等多方面原因综合所致。实验与数值模拟的对比证实，借助以上数值方法求解室内天然气爆炸与泄爆瞬态流场是可行的。

2 研究方案

由于民用建筑内天然气爆炸通常始发于厨房内，因此基于中国民用建筑厨房典型几何尺寸以及内部装修布置特征，选择房间模型尺寸为5 m(长)×2 m(宽)×2.5 m(高)。模型四周及屋顶和地板均为刚性壁面，其中较小面积的一面墙体上设置1个尺寸为0.5 m×0.5 m的具有一定开启压力的泄爆面。为准确描述泄爆口外部二次爆炸对室内爆炸灾害的影响，将计算域延泄爆口方向向外延伸1倍房间长度，并将延伸的该部分计算域设置为自由出流边界。采用尺寸为0.1 m的正方体结构网格对计算域进行离散。点火源位于房间后壁墙体的几何中心位置。由于天然气的主要成分为甲烷，在房间内均匀填充9.5%浓度且静止状态的甲烷/空气预混气体，计算域内的环境初始压力和初始温度分别设定为1.013 25×105Pa和300 K。

根据民用建筑窗体玻璃类型的不同，其静开启压力在7～60 kPa[2]，为研究房间内窗体不同静开启压力对室内天然气约束泄爆效应的影响，在研究中改变泄爆面的静开启压力，分别设为20，40和60 kPa。同时为研究房间内大尺度障碍物对天然气约束泄爆的影响，在房间内分别设置了体积阻塞率为0，0.15和0.30的障碍物。民用建筑厨房内的障碍物通常布置在房间四周，根据中国民用厨房结构特征，可以分为“I型”、“Ⅱ型”、“U型”、“L型”4类，本文采用“Ⅱ型”的厨房布置形式，即沿着房间底部和顶部两侧长度方向设置障碍物。房间内障碍物尺寸参照中国典型厨房中的橱柜、吊柜的尺寸和形式，位于下部的橱柜和位于上部的吊柜横截面尺寸分别为0.85 m(高)×0.5 m(宽)和0.65 m(高)×0.5 m(宽)，橱柜和吊柜的长度均与房间长度一致，此时房间体积阻塞率为0.3，而采用将橱柜和吊柜的高度降低一半的方法来实现阻塞率为0.15的实验条件。根据房间长度，在模型中设置了8个测点，所有测点均位于房间中心轴线上，除了点火源附近和泄爆面两侧的测点外，其余测点均按照1 m等间距布置。厨房结构以及测点布置如图3所示。

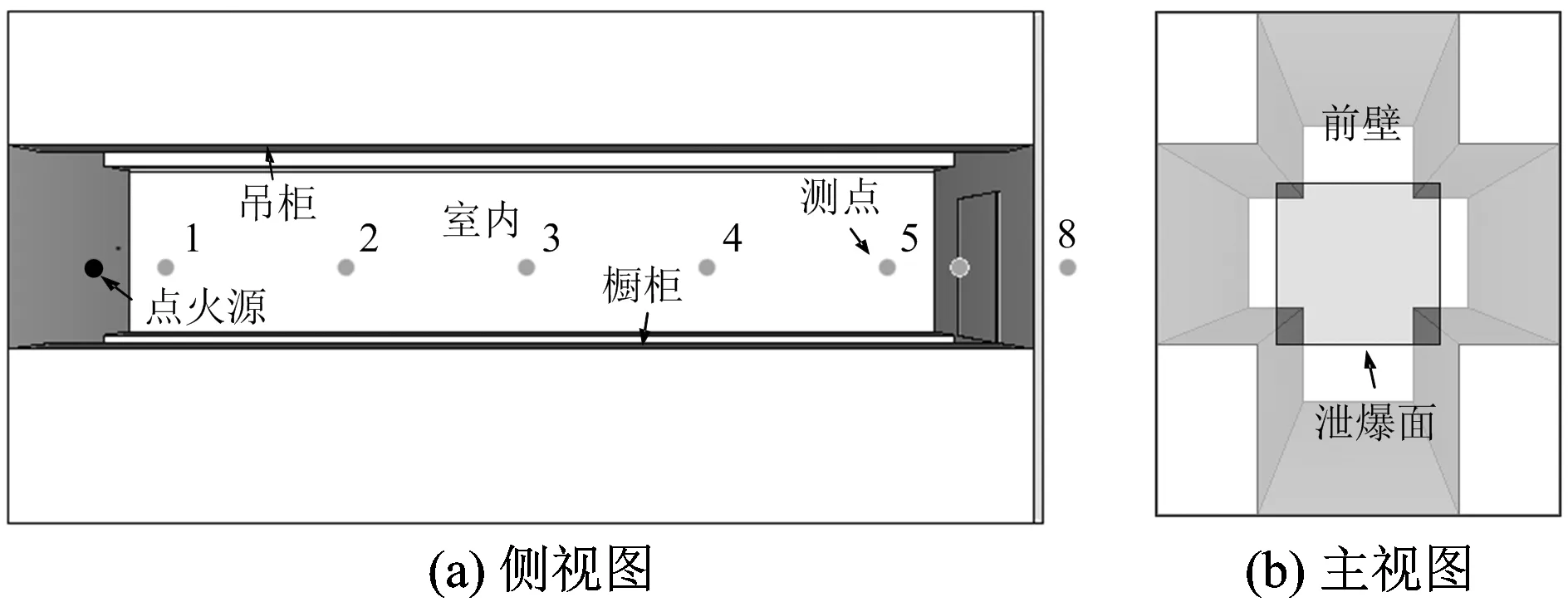
图3 典型厨房及内置大尺度障碍物的物理模型Fig.3 Physical model oftypical kitchen with built-in large scale obstacles

3 结果与讨论

3.1 无障碍物时不同开启压力对应的室内爆炸过程分析

图4给出了空房间内不同开启压力对应的室内轴线上的火焰速度。显然，各组火焰速度整体呈增长趋势，但火焰速度增长相对较慢，且涨幅较小。同时，最大火焰速度随着泄爆面开启压力的增加而不断增大，表明开启压力对火焰速度存在影响。这是由于开启压力越大，泄爆时刻房间内和房间外的压差也越大，泄爆引发的气体出流速度更快，进而沿泄爆口的火焰速度增加最为显著。

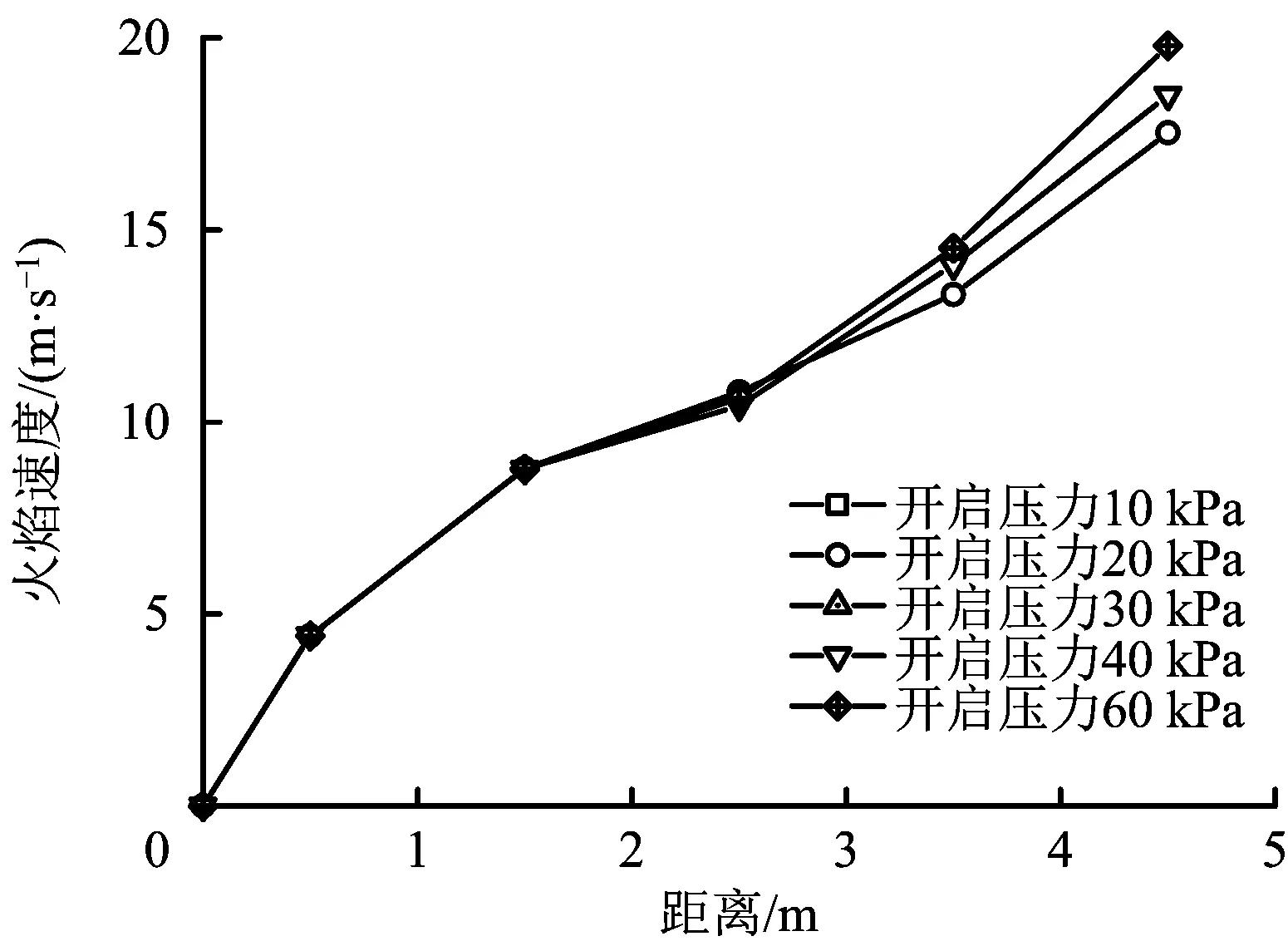
图4 无障碍物房间内不同开启压力对应的火焰速度-距离Fig.4 Flame speed-distance in unobstructed rooms with different activation overpressures

图5给出了空房间内不同开启压力对应的房间中心位置的爆炸超压随时间的分布，可见，每条曲线均呈现2个明显的超压峰值，超压峰值p1是由房间泄爆面开启造成的，而超压峰值p2则是由室内外压力平衡以及外泄气体二次爆炸等综合作用所致。2个峰值均随开启压力的增加而显著增大。随着泄爆面开启压力增加，室内气体的出流速度和湍流强度进一步增加，火焰速度进一步加快，进而气体燃烧速度和燃烧产物也随之增加，泄爆面开启后房间内外压力平衡需求和外部二次爆炸对室内流场的作用也更为强烈，最终导致室内更大的超压峰值p2。

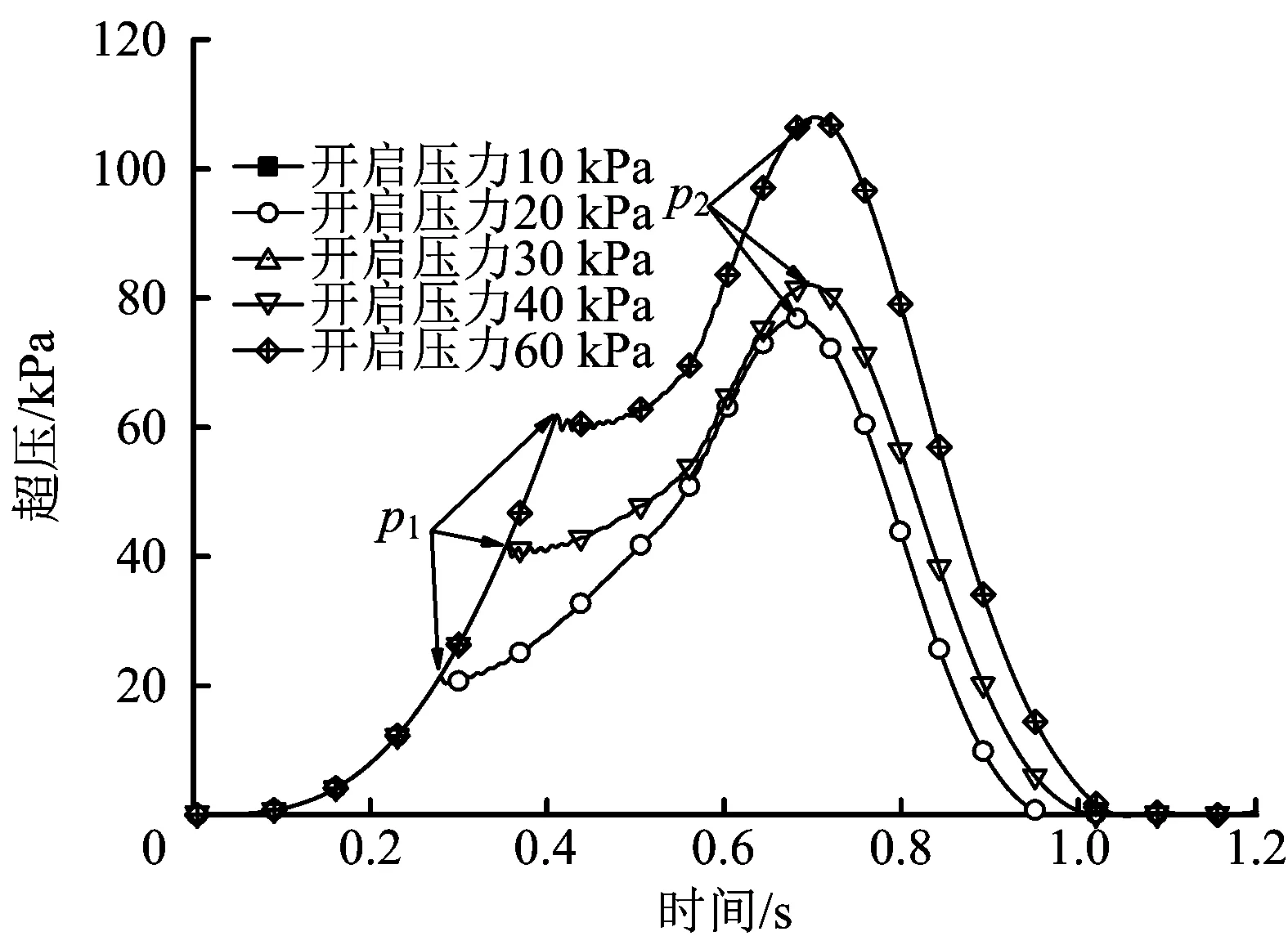
图5 无障碍物房间内不同开启压力对应的超压-时间Fig.5 Overpressure-time at centric position in unobstructed rooms with different activation overpressures

3.2 有障碍物时不同开启压力对应的室内爆炸过程分析

图6(a)和图6(b)分别为体积阻塞率为0.15和0.3对应的室内火焰速度分布。显然，各组火焰速度总体上呈现增长趋势，且沿传播距离均可以分为3个类似阶段。第1阶段是火焰缓慢增长阶段，出现在距房间后壁2 m范围内，该范围内火焰速度小于10 m/s。第2阶段是火焰快速增长阶段，出现在距房间后壁2 m至4 m范围内，该范围内火焰速度介于10 m/s与70 m/s之间。第3阶段是火焰波动阶段，该范围内火焰速度产生波动，但总体上处于较大的速度值。出现波动是由于该区域靠近泄爆口，泄爆面开启作用于气体流动，造成了火焰速度的不稳定性。

对比图4和图6发现，相对于开启压力，障碍物对促进火焰速度增长的影响更为显著。由于障碍物是普通房间内的主要湍流源，对爆炸灾害的传播过程主要表现为剪切作用，诱发火焰锋面前端的未燃气体形成湍流，从而进入火焰速度增加的正反馈机制。当厨房内的大尺度障碍物采用“Ⅱ型”布置时，由于障碍物沿房间长度方向布置，并没有改变火焰传播的总长度。因此，障碍物体积阻塞率的增加虽然导致房间内可燃气体的体积减小，但同时也促使实际爆炸有效空间的长径比增加，造成气体流速相对增加，最终导致火焰速度更早地进入快速增长阶段。

图6 有障碍物时不同开启压力对应的火焰速度-距离Fig.6 Flame speed-distance in obstructed rooms with different activation overpressures

图7(a)和图7(b)分别为体积阻塞率0.15和0.3时不同开启压力对应的超压时间曲线。当阻塞率为0.15时，超压峰值p1和p2均随开启压力的增加而增大，峰值到达时间也随之增加。当阻塞率为0.3时，峰值p1越发不明显。阻塞率的增加导致火焰速度增加更为迅速，促使气体生成速率明显大于气体泄放速率，房间内压力在极短时间内到达峰值，而泄爆面开启对室内超压的影响随着测点远离泄爆口而发生延迟，进而p1还未及时形成便进入火焰快速增长阶段。总体而言，随着体积阻塞率增加，泄爆面开启压力对峰值超压p1的影响逐渐降低。

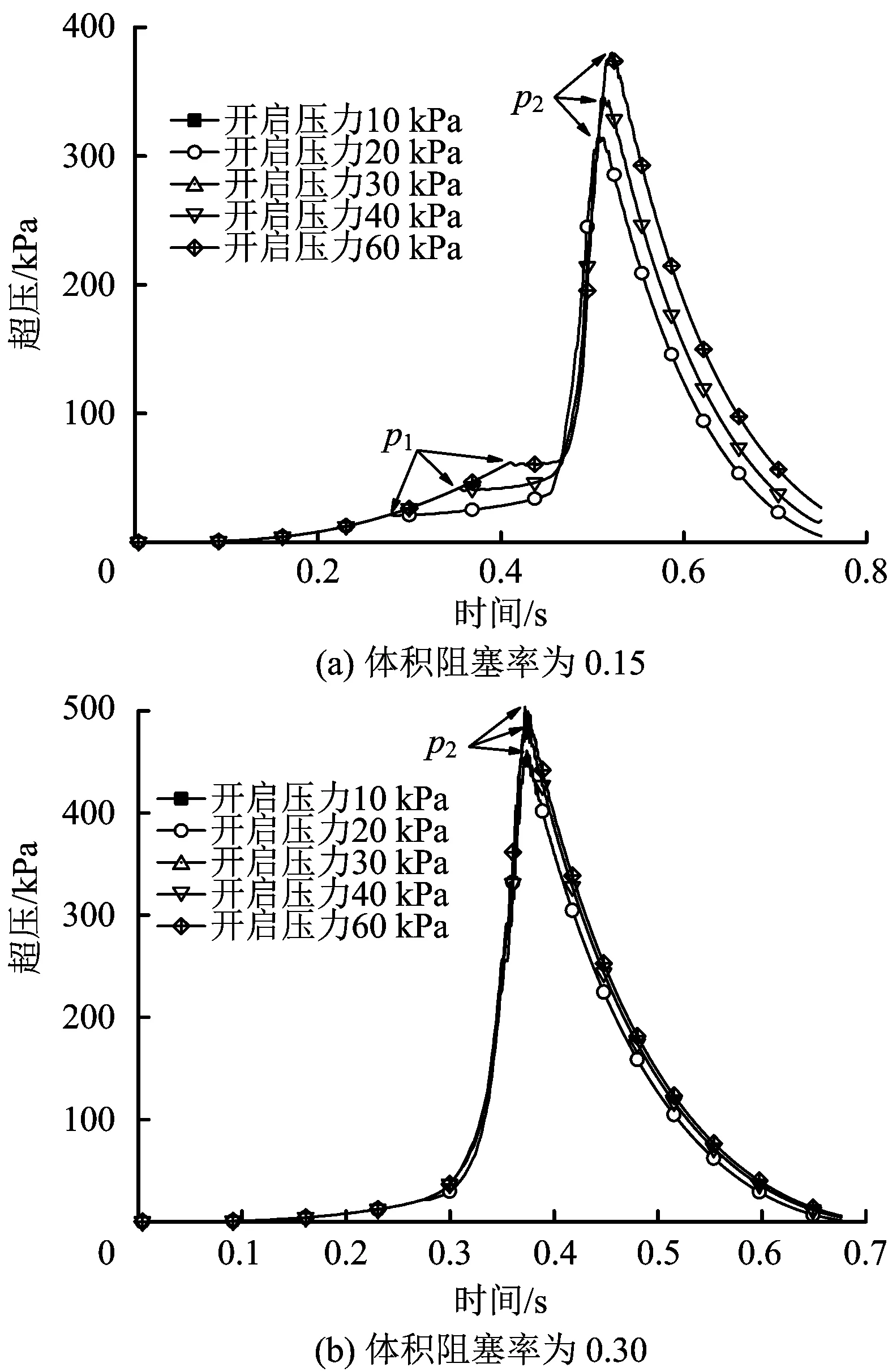
图7 有障碍物时不同开启压力对应的超压-时间Fig.7 Overpressure-time at centric position in obstructed rooms with different activation overpressures

3.3 泄爆面与大尺度障碍物的协同效应分析

图8为房间内不同阻塞率时最大火焰速度随泄爆面开启压力的变化。显然，最大火焰速度出现于最大开启压力和最大体积阻塞率同时存在时，但相比于泄爆面开启压力，障碍物体积阻塞率对火焰速度的影响更为显著。从图中可见，当室内阻塞率为0.15时最大火焰速度增长最快。可能是由于当房间内阻塞率为0时，室内湍流源较少，火焰速度相对较低，随开启压力的增长也较缓慢；而当阻塞率超过0.3时，大体积障碍物的存在一方面会导致室内可燃气体量减少，另一方面也会对火焰加速传播产生一定的阻碍作用。

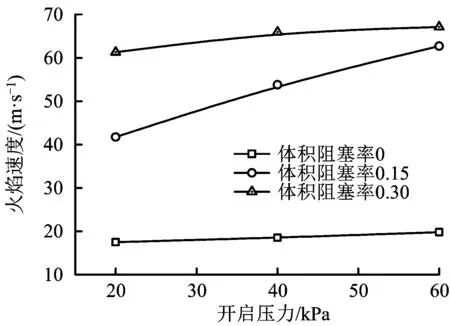
图8 不同体积阻塞率对应的最大火焰速度-开启压力曲线Fig.8 Peak flame speed-activation overpressure with different volume blockages

图9 不同体积阻塞率对应的峰值超压-开启压力曲线Fig.9 Peak overpressure-activation overpressure with different volume blockages

图9为房间内不同阻塞率时峰值超压随泄爆面开启压力的变化趋势。可见，峰值超压出现于最大开启压力和最大体积阻塞率同时存在时，即阻塞率与开启压力对室内峰值超压的增长产生了协同作用，共同促进其增长，但相比于泄爆面开启压力，障碍物体积阻塞率对超压发展的影响更为显著。

图10为不同体积阻塞率时室内峰值超压到达时间随开启压力的变化曲线。

图10 不同体积阻塞率对应的峰值超压到达时间-开启压力曲线Fig.10 Arrival time of peak overpressure-activation overpressure with different volume blockages

由图10可见，峰值超压到达时间现于最大开启压力和最大体积阻塞率同时存在时，这表明大尺度障碍物与开启压力对峰值超压到达时间也具有协同作用，共同促进超压快速发展，缩短峰值超压到达时间，最短的峰值超压到达时间出现于最大开启压力和最大体积阻塞率同时存在时。同时，相比开启压力，障碍物体积阻塞率对峰值超压到达时间的影响也更显著。

4 结论

1)大尺度障碍物与泄爆面对室内天然气爆炸过程具有显著的协同作用，共同促进火焰速度与爆炸超压的显著增长，并缩短峰值超压到达时间。在室内天然气爆炸事故调查分析过程中，应对这一协同作用给予足够重视，孤立分析单一因素容易低估爆炸强度。

2)相比泄爆面开启压力，大尺度障碍物体积阻塞率对泄爆效应的影响更为明显。尽管障碍物的存在显著减少了参与爆炸的天然气量，但从增加房间内湍流源和房间相对长径比的角度来衡量，大尺度障碍物对爆炸过程具有加剧作用。而随着开启压力的增加，障碍物对泄爆效应的影响更为强烈。在民用住宅天然气爆炸事故调查时，应对室内家具、电器等大尺度物品所形成的体积阻塞给予更多关注。

3)火焰峰面是天然气爆炸事故的主要致灾因素之一。大尺度障碍物与泄爆面协同作用下，室内火焰速度沿泄爆方向呈现出缓慢增长、快速增长、波动3个阶段。这一特征加剧了室内人员烧伤的复杂性和严重性，在灾害后果评估中应予以考虑。