基于GA-BP神经网络的粗粒土渗透系数预测

饶云康，丁 瑜,2,3，倪 强，许文年,2,3，刘大翔,2,3，张 恒

(1.三峡大学三峡库区地质灾害教育部重点实验室，湖北宜昌 443002；2.防灾减灾湖北省重点实验室(三峡大学)，湖北宜昌 443002；3.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北宜昌 443002；4.嘉兴市规划设计研究院有限公司，浙江嘉兴 314050)

根据规范[1]，粗粒组(粒径在0.075～60 mm之间)质量分数大于50%的土即为粗粒类土，简称粗粒土。粗粒土作为建筑材料、基础填料以及渗滤填料在水电、建筑、道路、市政等众多工程领域广泛应用，其力学特性、渗透特性是岩土工程、水利工程等热切关注和研究的内容[2-3]。实际工程中，粗粒土涵盖的范围十分广泛，粒径尺寸差异巨大，加之压实状态变化，其渗透性能呈现明显差异。因此，如何准确预测粗粒土的渗透系数，对于相关工程的渗透分析、防渗设计具有重要意义。

渗透系数是表征土体渗透性能的宏观参数，受诸多因素影响，其中，颗粒级配和孔隙比是最主要的两个因素[4-6]。众多学者们围绕颗粒级配、孔隙比开展了大量试验研究[7-10]。基于试验成果总结，学者们提出了一些用于估算粗粒土渗透系数的经验公式[11-12]。经验公式变量主要为某些表征颗粒级配的指标，有些也包括孔隙率或孔隙比。采用经验公式估算粗粒土渗透系数，不同公式的计算结果差异较大，往往与实测结果不符[13-14]。由于试验数据有限和未能充分考虑各个粒径颗粒含量和孔隙比的影响，经验公式适用范围有限。

针对上述不足，一些学者采用人工神经网络方法预测渗透系数。唐晓松等[15]采用BP神经网络，由颗粒级配预测了粗粒土渗透系数。王双等[16]以d10～dmax表征全级配，采用BP神经网络方法研究了碎石土级配对渗透系数的影响。文献[16]的研究指出，级配不是反映渗透系数唯一决定表征，但该文未考虑孔隙比影响。合理地预测粗粒土渗透系数必须充分考虑各个粒径颗粒含量和孔隙比的影响。

若BP神经网络初始权值和阈值设置不合理，存在收敛速度慢、陷入局部最优等问题[17]。为克服上述不足，可利用遗传算法对网络的初始权值和阈值进行优化，在较大范围进行搜索，代替一般的随机选取，然后应用BP网络算法对其进行精调，搜索出最优解或近似最优解[18]。为此，本文通过相关文献选取93组粗粒土试验数据，考虑粒径累计曲线中的d10～d100和孔隙比，利用遗传算法优化BP神经网络的初始权值与阀值，构建基于BP神经网络和遗传算法的粗粒土渗透系数预测模型。

1 样本选取与数据处理

1.1 样本选取

粗粒土渗透系数受诸多因素影响，如颗粒粒径、各级粒径颗粒分配情况、密实程度、颗粒形状等。颗粒级配是颗粒粒径、各级粒径颗粒分配的综合反映；孔隙比不仅直接与土体密实程度密切相关，也与颗粒形状有关。为此，以颗粒级配、孔隙比为主要因子选取样本，对粗粒土渗透系数进行预测。

通过查阅，分别从文献[11]，[19]，[20]，[21]，[7]，[8]和[22]整理得到11，12，5，31，13，10和11组粗粒土渗透试验样本数据，共93组。样本数据的渗透系数直接来自于文献，是基于达西定律采用常水头试验测定的饱和渗透系数。渗透系数都是标准温度(20 ℃)下的渗透系数k20，避免了温度不同的影响。除渗透系数外，各样本既包括颗粒级配信息，又包括直接或间接的孔隙比参数。

规程[23]指出，当粗粒土中的细颗粒含量(小于0.075 mm)不超过12%时，土样不会因为细粒土含量过多而产生黏聚力，能自由排水。所选的93组样本均属于规范[1]的粗粒土定义范围，且样本的细颗粒含量(小于0.075 mm)均不超过12%，属于颗粒之间无黏聚力的能自由排水的粗粒土。选取的样本渗透系数数量级主要为10-3～10-1cm/s，少量为10-4cm/s，为典型的粗粒土渗透系数范围。最大粒径为100～5 mm，既有大粒径也有小粒径的粗粒土。样本的孔隙比最大为0.712，最小为0.093。样本的渗透系数、颗粒粒径、孔隙比涵盖范围广，具有代表性。

1.2 数据处理

对于93组数据，采取如下数据处理方式：

(1)孔隙比：若文献中给出了孔隙比，则直接采用；若没直接给出孔隙比，则根据文献提供的其他物理指标，由公式换算得出。

(2)颗粒级配：考虑了以往研究很少关注的粒径d100，以d10,d20,…,d100表征颗粒全级配。首先，根据样本数据利用Excel绘制粒径累计曲线；然后，由粒径累计曲线获取全级配d10～d100粒径。为避免手工操作误差，利用图表数字化工具(GetData Graph Digitizer)从粒径累计曲线中准确获取粒径。

2 GA-BP神经网络预测模型

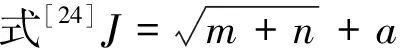
BP神经网络传统的梯度下降法具有收敛速度慢、易陷入局部最小值等缺陷，而Levenberg-Marquardt(L-M)遗传算法可改善传统算法的缺陷，提高网络的收敛速度，以及增加网络训练精度[25]。为此，网络训练函数采用trainlm函数，trainlm函数使用L-M算法，学习速率基值为0.001，学习速率减少率为0.1，学习速率增加率为10，最大学习速率为1010。

GA-BP神经网络模型通过Matlab软件编程实现，遗传算法采用gaot工具箱，基本步骤如下：

(1)数据归一化，划分样本。导入93组样本数据，将样本数据归一化到[-1,1]，随机选择6组样本作为检测样本，剩余87组作为训练样本。

(2)建立BP神经网络。网络采用3层结构，输入层有11个神经元，分别代表d10,d20,…,d100和孔隙比；输出层神经元为渗透系数；隐含层有12个神经元；隐含层传递函数为tansig函数，输出层传递函数为purelin函数，网络性能函数采用均方误差mse函数；最大迭代次数为1 000次，目标误差值为5×10-6，最低性能梯度为10-10。

(3)产生初始种群。编码方式采用浮点数编码，个体由输入层与隐含层、隐含层与输出层神经元之间的连接权值，隐含层和输出层的阈值4部分组成，BP神经网络为11-12-1结构，因此，个体编码长度为11×12+12×1+12+1=157。个体中的变量范围为[-3,3]，种群规模为50。

(4)解码，计算适应度。解码个体得到BP神经网络的初始权值和阈值，采用训练样本的网络计算值与试验值的均方差作为目标函数值，将目标函数值的倒数作为适应度，适应度越高，均方差越小，则该个体越优良。

(5)选择、交叉、变异，产生新种群。选择操作采用轮盘赌法选择算子；交叉操作采用算术交叉算子，即2个个体经过线性组合产生2个新的个体；变异操作采用非均匀变异算子。

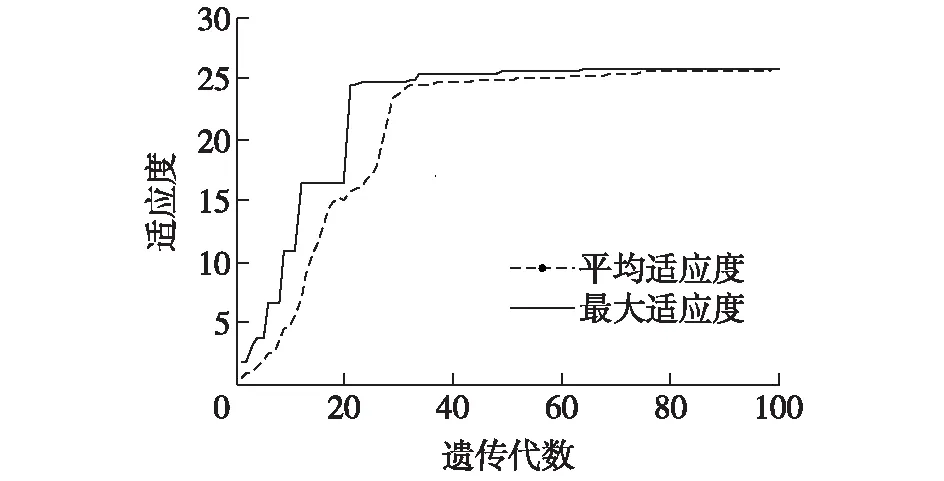
图1 适应度进化曲线Fig.1 Fitness evolution curves

(6)重复步骤(4)和(5)，直至达到最大遗传代数100。种群适应度进化曲线如图1所示，进化75代后种群的最大适应度保持不变，平均适应度与最大适应度基本重合，此时得到最优个体。

(7)解码最优个体得到优化的初始权值和阈值。

(8)采用优化后的初始权值和阈值，利用训练样本训练神经网络。

(9)通过检测样本检验网络模型的泛化性能。

3 结果分析与讨论

3.1 模型收敛速度

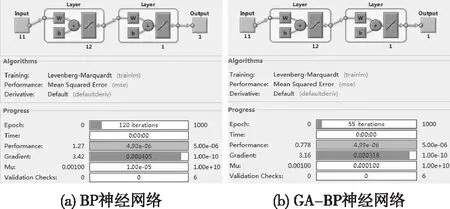
图2 网络训练窗口Fig.2 Neural network training window

分别采用BP神经网络和GA-BP神经网络两种方法建立粗粒土渗透系数预测模型进行对比研究。图2为两种方法的训练窗口。BP神经网络经过120次迭代之后达到目标误差值5×10-6的要求，而采用相同的参数设置，GA-BP神经网络只需55次迭代就能达到目标误差值。表明遗传算法能优化得到合理的BP神经网络初始权值和阈值，能明显提高BP神经网络的收敛速度。

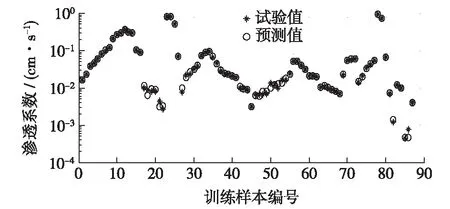
图3 训练样本的预测结果Fig.3 Predicted results of training samples

3.2 训练样本验证

用建立的GA-BP神经网络模型预测训练样本，结果如图3所示，平均相对误差为5.10%，其中有75%的样本相对误差小于平均相对误差，渗透系数预测值与试验值较接近，相对误差在可接受范围，精度较高。BP神经网络模型对训练样本的预测误差与GA-BP神经网络相差不大。

3.3 预测精度及泛化性能

神经网络预测精度的评价指标主要为相对误差和平均相对误差，为了检验和比较两种模型的预测精度和泛化性能，分别用两种模型预测6组检测样本。6组检测样本来源于5篇文献，孔隙比最大为0.548，最小为0.121。检测样本最大粒径为60～5 mm，且渗透系数试验值数量级涵盖10-3～10-1cm/s，具有代表性。

检测样本的两种模型预测结果与试验结果如表1所示，采用GA-BP神经网络的最大相对误差为10.44%，平均相对误差为6.39%，渗透系数预测值与试验值较接近，相对误差在可接受范围，表明该神经网络的泛化性能良好。而采用BP神经网络，最大相对误差为31.97%，平均相对误差为12.64%，预测误差明显高于GA-BP神经网络，表明GA-BP神经网络模型的泛化性能优于BP神经网络。

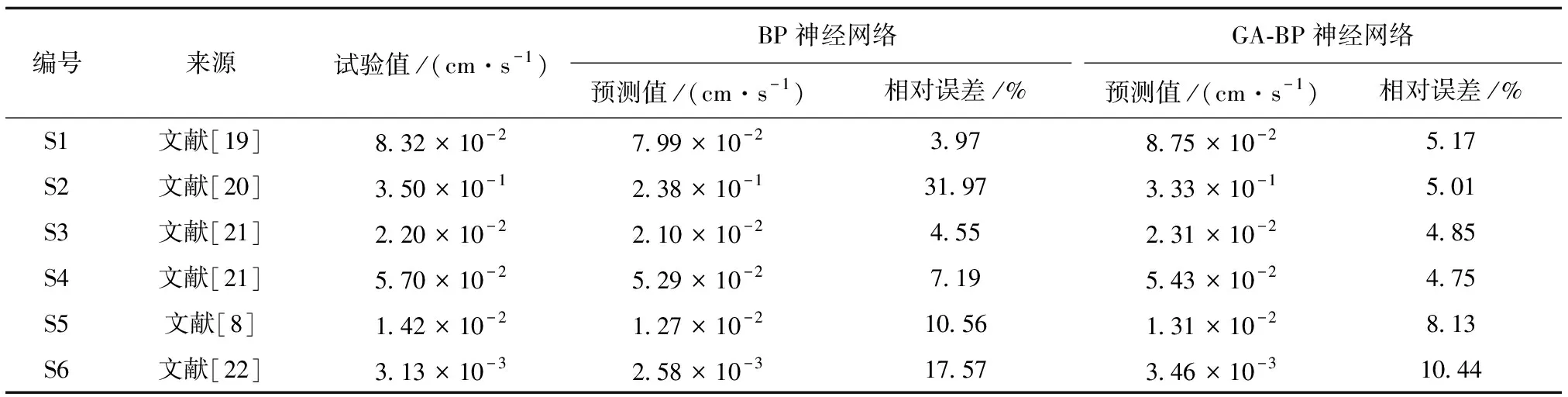
表1 检测样本的预测结果Tab.1 Predicted results of testing samples

全级配和孔隙比表征粗粒土自身性质，而试验过程中的击实操作导致的颗粒破碎会使粗粒土级配略有改变，渗透试验存在边壁效应和尺寸效应[3]等均会影响渗透系数试验结果，因此神经网络的渗透系数预测值与试验值存在误差是正常的。

综上所述，考虑全级配和孔隙比建立GA-BP神经网络模型，其预测值与试验值较吻合，且具有较好的泛化性能。颗粒级配和孔隙比是粗粒土渗透系数的主要影响因素，该神经网络能充分反映颗粒级配和孔隙比对粗粒土渗透系数的影响。研究表明，采用GA-BP神经网络，由全级配和孔隙比能较好地预测粗粒土渗透系数，可为实际工程中粗粒土选配与改善提供参考依据。

4 结 语

考虑全级配d10～d100和孔隙比，分别采用BP神经网络和GA-BP神经网络构建粗粒土渗透系数预测模型，得出主要结论如下：

(1)BP神经网络和GA-BP神经网络分别经过120次和55次迭代之后达到相同的目标误差值。分析6组检测样本的预测结果，BP神经网络的最大相对误差为31.97%，平均相对误差为12.64%，而GA-BP神经网络的最大相对误差为10.44%，平均相对误差为6.39%。表明遗传算法能优化得到合理的BP神经网络初始权值和阈值，能明显提高BP神经网络的收敛速度，所建模型预测精度较高且泛化性能较好。

(2)87组训练样本预测结果的平均相对误差为5.10%，6组检测样本预测结果的平均相对误差为6.39%，表明GA-BP神经网络模型能充分反映颗粒级配和孔隙比对粗粒土渗透系数的影响，采用GA-BP神经网络，由全级配和孔隙比能较好地预测粗粒土的渗透系数。

(3)收集各工程渗透试验数据，建立神经网络大数据平台，可为后续粗粒土工程渗透系数的预估提供参考。