系泊平台碰撞外部动力学的数值仿真研究❋
2019-01-04段秋婉
段秋婉, 杨 飏
(大连理工大学船舶工程学院, 辽宁 大连116024)
碰撞是引起船舶与海洋结构物损伤的重要因素,也是船舶工程上的热点问题。海洋平台一般在海况恶劣的深海海域工作,由于作业需要,附近常有穿梭油轮和供应船的航行或停靠,因此系泊状态下的平台被碰撞的机会较多。
对于复杂的碰撞问题,有限元分析方法和简化解析法具有高效、简便和精确的优点,因此应用最为广泛。
目前,非线性显式有限元软件能够精确地计算碰撞力和结构损伤,模拟船体的运动过程。学者们通过研究碰撞有限元法的关键技术,提高数值仿真结果的准确性。顾永宁等[1]阐述了材料本构和网格质量对计算结果精确程度的直接影响;Getter[2]等通过确定钢材断裂极限应变和应变率等材料参数,保证分析结果的正确性;Sören[3]得到失效应变与单元长度的关系曲线,为有限元建模和参数设置提供了依据。
在简化解析方面,学者们建立不同的力学模型,多角度解释了碰撞机理。Minorsky[4]根据完全非弹性碰撞理论,求解船舶舷侧撞击时的能量耗散,提出简化解析公式。Pedersen和Zhang[5]提出外部动力学的二维理论模型,利用动能定理和动量方程,求解碰撞系统的耗散能,与Minorsky[4]的计算结果相吻合。Stronge[6]针对多种碰撞形式,阐述了刚体的三维碰撞理论解法。Liu和Amdahl[7]基于Stronge[6]的理论发展了局部坐标系下的三维碰撞理论,验证结果的准确性。
本文研究的被撞平台主船体和系泊系统以一定的方式相连接,组成多体系统。多体系统的碰撞问题有两种解决思路:“分段”分析法将碰撞过程视为瞬时的,分别对碰撞前后进行动力分析。Wehage[8]首次通过求解平衡、动量和冲量方程,获得碰撞后的结果,并根据多体连接处的铰接形式,建立约束方程求解其运动状态。“连续”分析法将碰撞载荷视为持续作用力,把各时刻的碰撞力作为已知载荷加入系统方程求解。Khulief和Shabana[9]采用等效质量法简化多体系统,并验证曲轴连杆算例。Lankarani和Nikravesh[10]基于两球碰撞模型推导出碰撞力与撞深的函数关系,并应用于Khulief[9]的连杆系统。
本文采用ANSYS建立了单点系泊状态下的平台模型,其中系泊装置间连接部分的模拟是本文的难点。使用LS-DYNA计算了不考虑流体情况下,平台在碰撞载荷作用下的运动状态。基于外部动力学理论,对比了有、无系泊工况的结果,探究平台整体运动的普适性规律。
1 碰撞有限元分析方法
本文采用显式有限元数值仿真方法分析碰撞过程,其基本原理是:将碰撞体模型离散化,定义合适的时间步长Δt,根据t时刻的位移计算碰撞力,建立t+Δt时刻的运动方程,采用中心差分法求解出该时刻的位移。由于中心差分法是条件稳定的,设定的时间步长Δt应满足以下关系:
(1)
式中:α为时步因子,根据经验取0.9;Lmin是模型最小单元长度;材料声速c通过式(2)计算。
(2)
式中:E为材料的弹性模量;ν为泊松比;ρ为材料密度。
1.1 碰撞力计算
在每个时间步上,应将载荷作为已知条件施加到结构上,需优先计算。通过罚函数法可计算平台和船之间的碰撞力:在两碰撞体的接触面上定义主、从节点,考察各时刻从节点是否穿透主面;若没有穿透,不做任何处理;若穿透,则在主、从面间引入法向接触力,其大小与穿透深度、主面的刚度成正比。
(3)
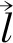
(4)
式中:f为接触刚度比例因子,取0.1;Ki为接触单元的体积模量;Ai为主面的单元面积;Li为接触单元的最大对角线长度。
将作用在主面上的接触力-fs(法向接触力的反作用力)等效分配到主单元(通常是是四节点单元)的节点上:
fjm=-φjfs,j=1,2,3,4。
(5)
式中:fjm为主单元等效接触力;φj为主单元面上的二维形函数,下标j为节点号。
1.2 建立碰撞运动方程
本文采用更新拉格朗日算法建立t时刻的运动方程。将平台和船的结构空间离散化,单元上任一质点X在t时刻的位移ui(X,t)为[12]:
ui(X,t)=NIuiI(t)。
(6)
式中:NI为单元内的形函数;uiI(t)为单元上节点I的位移,下标i为坐标系方向。对ui(X,t)作变换可得:
(7)

虚功率方程表示为:
(8)
式中:ρ为t时刻的密度;σji为应力张量;bi为作用在物体单位质量上的力。
将式(7)写成矩阵形式,代入虚功率方程(8)中,整理得到碰撞的运动方程:
(9)
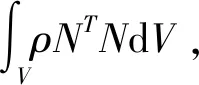
1.3 多体系统约束方程的建立
由于平台是主船体和系泊装置所组成的多体系统,各部分的位移相互约束,系统的运动方程不同于单体,因此需要对式(9)进行补充。
对于N个质点组成的系统,一阶线性约束方程表示的限制条件为:
(10)
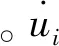
(11)
式中,λ为拉格朗日乘子向量,系数满足Cq(u,t)=0。
1.4 节点位移求解
基于以上结果,假定0~(t-Δt)时刻的节点位移、速度和加速度均已求得,利用中心差分法求解t时刻的位移,迭代公式如下所示:
(12)
将式(12)代入式(11)中,反复迭代求出t时刻的节点位移。
2 碰撞分析模型
2.1 碰撞仿真模型
单点系泊FPSO平台和单点系泊系统如图1(a)所示,主尺度如表1所示,撞击船主尺度如表2所示。采用ANSYS软件建立有限元模型,LS-DYNA软件进行碰撞计算和后处理。为降低计算时间,将撞击船模型简化为刚性船首。平台和撞击船模型均采用SHELL163单元模拟。平台重量为24 610 t,重心在纵向上位于船后部距船中3.5 m,垂向上距基线7.6 m。

表1 平台主尺度
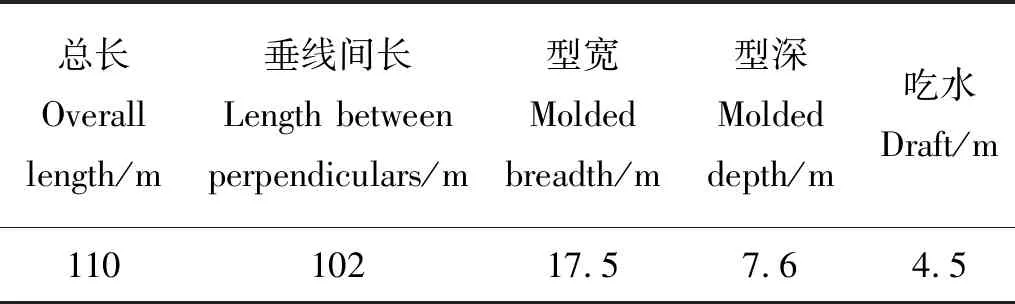
表2 撞击船主尺度Table 2 Principal dimension
平台模型共有255 087个单元,撞击船模型有4 388个单元,如图1(b)所示。
平台及撞击船所用钢材为船体235钢,材料本构采用线性强化的弹塑性模型,相关的参数为:材料密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3,硬化模量1.18 GPa。考虑到碰撞的应变率作用,钢材本构采用Cowper-Symonds模型,其本构方程为[13]:
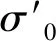

图1 带系泊系统碰撞船模型
2.2 系泊系统铰接模拟
本文将平台主船体与系泊装置作为多体系统考虑,在YOKE端部采用铰支,比一般碰撞问题中铰支或固支的单一主船体模型更为真实,在数值模拟方法上也更为复杂。系泊系统包括MSS、连接臂和YOKE,各构件之间以球铰相连。为了模拟构件间的球铰连接,建立如图2所示的模型,在构件端部增加圆锥面,使得两构件的连接集中于一点,采用Couple命令耦合两端点的平动自由度。这样,实现了构件端点处所有平动运动一致、转动不受限制,且其他部位互不影响的目的,简便地模拟了系泊装置的铰接。

图2 连接臂和YOKE之间的连接Fig.2 The joint between pendant and YOKE
2.3 碰撞场景设置
根据DNV-OS-A101给出的碰撞分析要求,给定排水量为5 000 t的撞击船以2 m/s的速度垂直于平台舷侧碰撞,撞击位置为船体后侧距船中15.2 m的堆舱处。
3 碰撞分析
3.1 碰撞力分析
图3对比了有、无系泊条件下碰撞力与撞深的关系曲线。由于系泊系统的约束作用,有系泊工况的最大碰撞力比无系泊大13.2%(1.4 kN),极限撞深大1.86%(0.007 7 m)。在曲线后半段(撞深0.3~0.45 m)上,两种工况的卸载路径均与相应的加载路径不同,说明碰撞力和撞深的关系具有路径相关性。
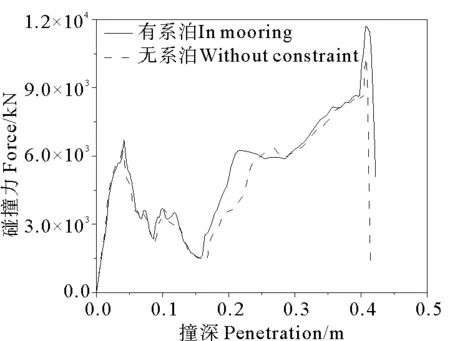
图3 碰撞力-撞深曲线Fig.3 Curves of collision force against penetration
图4展示了有、无系泊工况碰撞力随时间的变化趋势。由于碰撞中存在着大量的接触非线性,碰撞力经历多次加载和卸载过程,呈现反复波动的特征。碰撞力在0.36~0.76 s内显著下降,后又急剧上升。这是因为0.36 s之前,只有形状尖锐的撞击船上部与平台碰撞,接触单元的应力较大,碰撞力也因此较大;0.36~0.76 s内,撞击船上部因挤压发生形变,接触面积增大,应力也随之减小,碰撞力呈下降趋势;0.76 s后,撞击船下部球鼻艏也开始与舷侧接触,加速度急剧上升,使得碰撞力曲线呈上升趋势。1.3 s后,平台和船仍沿原方向运动,但彼此分离,碰撞力也随之降低。此外,对比两种工况的曲线情况,在0~1.3 s内,两种工况的曲线基本重合,说明此阶段系泊作用还未显现;在1.3 s后的碰撞力卸载阶段,无系泊工况的碰撞力直接降为0,而系泊工况降为0.25 kN(约为最大碰撞力的2%)左右并维持了约2.89 s,即有系泊工况的碰撞持续时间比无系泊长120%。
3.2 多体系统能量分析
图5比较了两种工况下平台舷侧外板和实肋板能量吸收的比率(结构变形吸收的能量与总能量的比值)。两种工况的同一舷侧结构在撞深0.1 m范围内吸能比率几乎相同;在0.1~0.4 m内,系泊工况比无系泊的吸能比大0.1%~0.9%;在最大撞深处,前者比后者大0.8%。撞击船的初始动能通过碰撞力做功,转化为平台的动能和舷侧构件的势能(即吸收的能量)。在系泊系统的约束作用下,碰撞强度和持续时间的增加导致碰撞力做功变大,因此舷侧构件的吸能比率也相应提高。对比同一工况的不同舷侧结构,舷侧外板的吸能比率比实肋板大2%~4%,在最大撞深处有、无系泊工况的舷侧外板吸能分别为15.3%和14.4%,实肋板吸能分别为12.6%和11.6%。舷侧板由于较大的膜拉伸变形,吸能较大,成为第一吸能构件,而实肋板因弯曲变形较小,吸能相对较少。
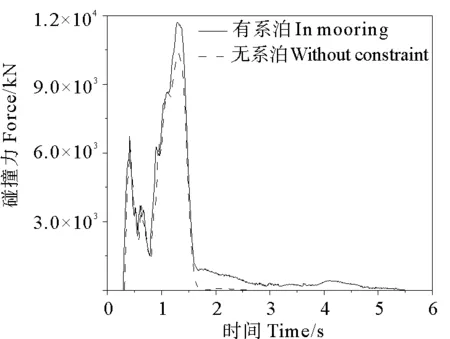
图4 碰撞力时程曲线Fig.4 Time history curves of collision force
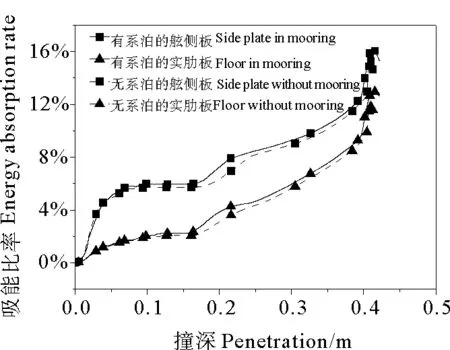
图5 舷侧能量吸收时程曲线Fig.5 Time history curves of energy absorption
3.3 平台运动响应分析
如图6所示,碰撞结束时有系泊工况的横荡速度大于无系泊,分别为0.37和0.26 m/s,大约是撞击船初始速度2 m/s的18.5%和13%,而纵荡和垂荡速度均小于0.03 m/s,说明相当一部分初始动能转化为平台在Y方向的动能,X、Z方向的平动影响很小。
图7中显示,在有、无系泊工况下横荡位移均最大,碰撞结束时达到1~1.5 m。而垂荡和纵荡位移在0.12 m以下,分别为横荡的7.19%和10.87%、4.77%和1.3%,说明在垂直舷侧碰撞中,平台最主要的运动是横荡,然而由于碰撞力的偏心作用,平台发生弯曲变形,产生了少量的垂荡和纵荡位移。
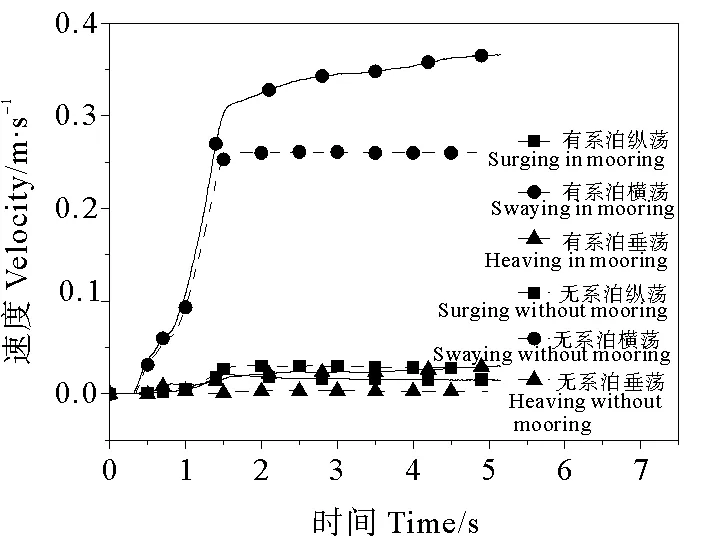
图6 速度时程图Fig.6 Time history curve of velocities
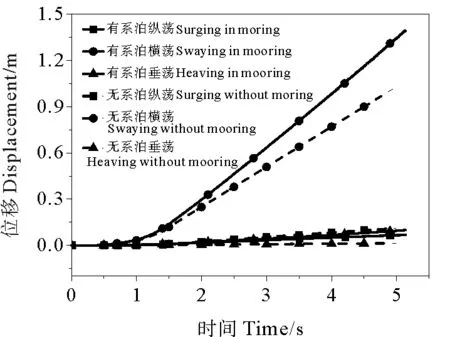
图7 位移时程曲线Fig.7 Time history curve of displacements
在Y方向上,一方面,有系泊状态的碰撞强度更大、持续时间更长,因此平台重心的横荡位移较大。在图7中,1.5 s后有、无系泊工况的横荡位移近似线性地增加至1.53和1.03 m,前者始终大于后者,并比后者高48.50%。另一方面,系泊系统对平台的整体偏转有限制作用,平台艏、尾位移远小于无系泊状态。图8显示,有系泊的艏、尾位移在3 m以下,仅为无系泊工况的25%。
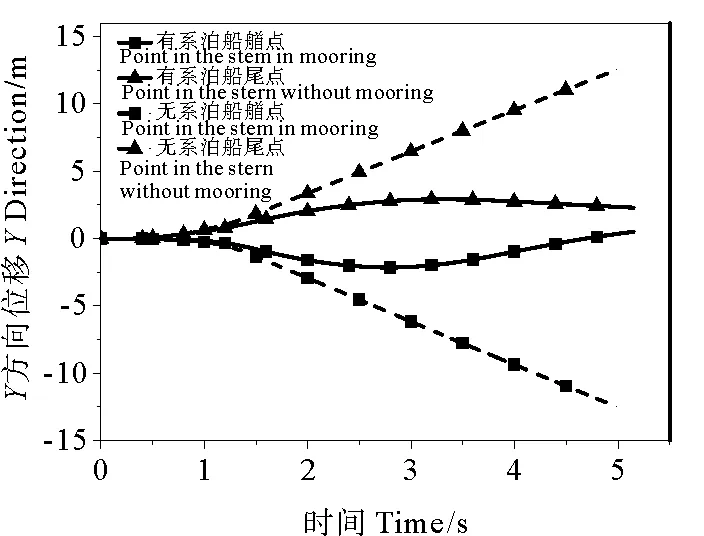
图8 Y方向位移时程曲线Fig.8 Time history curve of displacements in Y direction
无系泊状态下的碰撞过程可近似看做二维碰撞,如图7所示,垂荡位移只有0.0137 m,远小于X、Y方向的位移,可忽略不计。而在有系泊工况下,由于多体系统间的作用,平台在三个方向上的运动相互影响,因此纵荡和垂荡幅值分别降低和提高,导致碰撞扩展到三维空间。图中显示,在X方向,有系泊工况的纵荡位移始终小于无系泊工况,最大值为0.073 m,比后者低34.29%;在Z方向,垂荡位移则一直大于无系泊,在碰撞结束时上升到最大值0.11 m,是后者的8.1倍。
在图9中,平台在横摇、纵摇和艏摇角速度幅值在0~0.06 rad/s,由此判断,仅有少部分初始动能转化为平台的转动动能。其中纵摇角速度在零值附近波动,并且幅值极小,可忽略不计。与无系泊工况不同,有系泊工况横摇和艏摇的变化趋势近似正弦曲线,有一定的周期性。
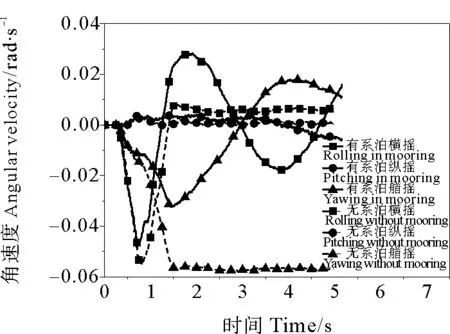
图9 角速度时程图Fig.9 Time history curves of angular velocities
在图10中,两种工况均是艏摇角度最大,横摇和纵摇角度幅值分别为艏摇的53.51%和14.11%、19.92%和2.78%,说明平台三个方向的旋转运动都比较明显,而艏摇最为剧烈。

图10 角度时程图Fig.10 Time history curves of angles
与平动位移类似,系泊系统极大地限制了平台的艏摇运动,同时平衡了纵摇和横摇运动。图9中显示,有系泊工况的艏摇角度始终远小于无系泊,其艏摇角度在3s时刻达到最大值2.56°,比无系泊工况的12.91°小80.17%;横摇角度于1.12 s达到最大值1.37°,比无系泊工况小25.05%;有系泊工况的纵摇角度于3.75s上升至最大值0.51°,比无系泊大41.67%。
总体来看,两种工况平台的运动情况有所不同:无系泊工况下平台的运动集中在X-Y平面内,发生剧烈的横荡和小幅纵荡运动,产生明显的右倾,同时匀速地顺时针旋转;有系泊工况下平台也发生右倾,在六个自由度上的运动均有变化,其中横荡、垂荡和纵摇幅值较大,艏摇、横摇和纵荡位移明显减小。
3.4 平台运行轨迹分析
系泊条件下,平台的系泊装置是整个多体系统的重要部分,其运动状态也影响着主船体的运动。将MSS与连接臂、连接臂和YOKE的铰点定义为D和D’、E和E’,YOKE的铰支端点定义为O,如图11所示。
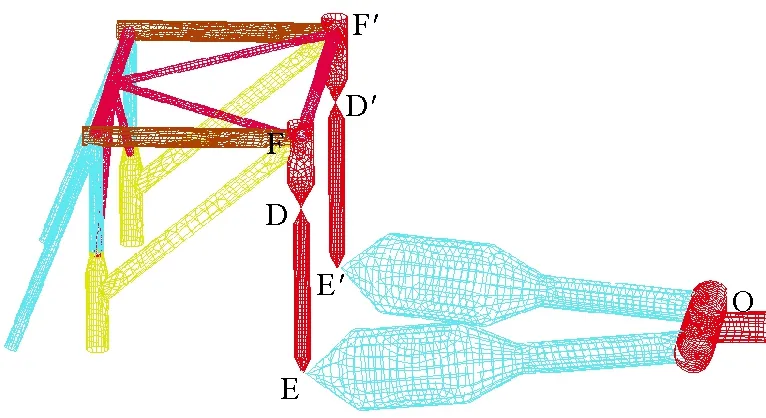
图11 系泊系统模型图Fig.11 the model of mooring system
图12和13展示了铰点E和E’、D和D’的运动轨迹在3个平面上的投影,分别反应了YOKE和连接臂的运动情况。
图12(a)和(b)显示,E和E’在Y-Z和X-Z平面上的路径完全对称,并且X-Y平面内的轨迹近似于直线(拟合度高达99%),拟合后的关系式为y=1.04×10-3-2.40x和y=-9.84×10-4+2.49x,可推断YOKE在过这两条直线的竖直平面内做圆周运动。由于受撞击位置的影响,YOKE左右两侧的运动趋势不同,因此两铰点的轨迹形状差异很大。E、E’在Z方向的位移变化范围分别是-0.3~0.2 m和-0.35~0.15 m,是X、Y的变化范围的10~20倍,说明YOKE在Z方向的运动更剧烈。
D和D’与平台主船体焊接在一起,又与连接臂的端点相耦合,其运动轨迹是复杂的三维曲线,如图12所示,其中Y方向的范围(-2~0.5 m)均为是X、Z的5倍。此外,D和D’点在X-Y平面内的轨迹关于Y轴(x=0)近似对称,即X方向位移反向,验证了3.3中的结论:连接臂对主船体的艏摇运动施加了回复力约束。
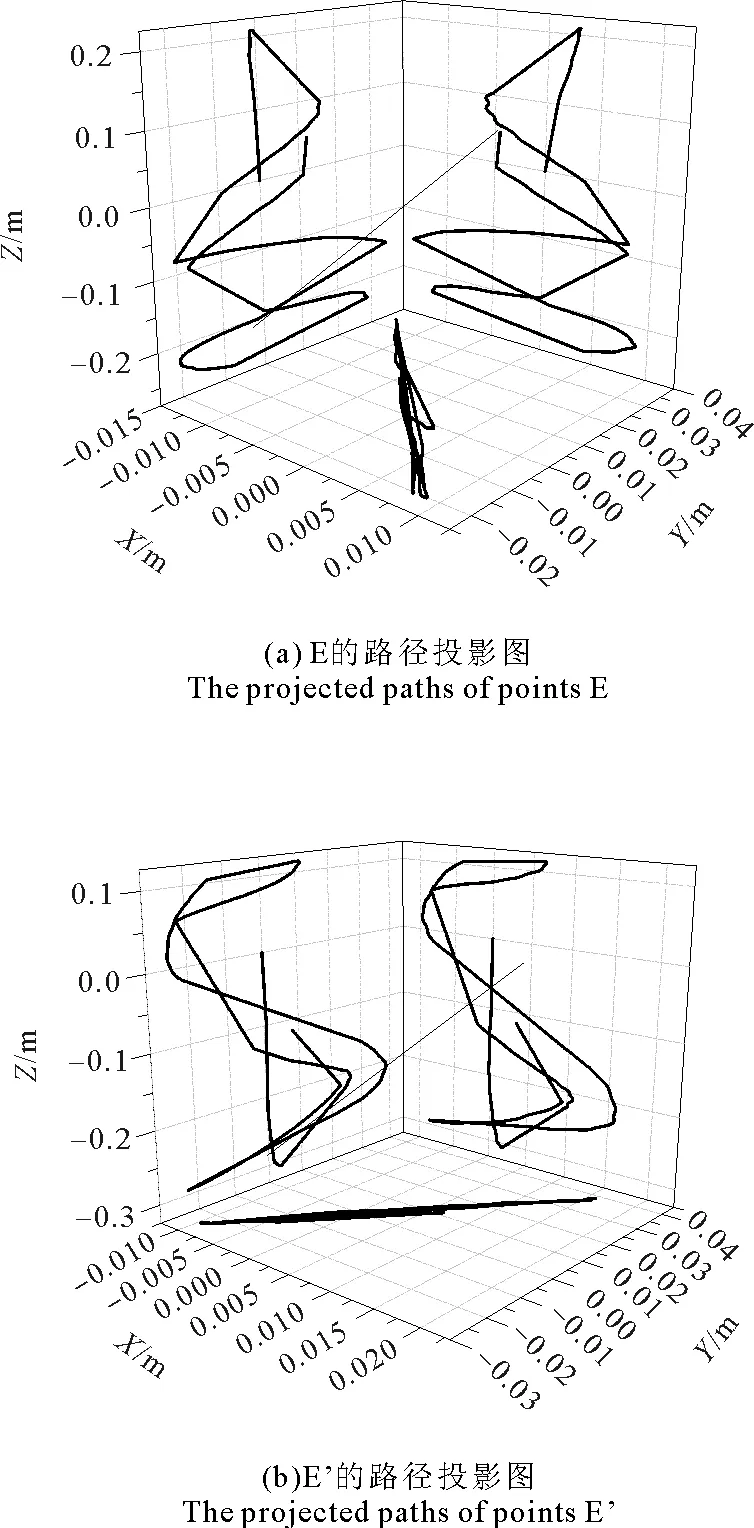
图12 YOKE与连接臂铰点E、E’路径投影图Fig.12 The projected paths of points E and E’
在图14中,连接臂和YOKE(左侧OE和DE、右侧OE’和D’E’)、MSS和连接臂(左侧ED和DF、右侧E’D’和D’F’)的夹角随主船体平动和旋转运动而变化,其变化量的时程图线与正弦曲线近似。OE和DE、OE’和D’E’的曲线大致对称,变化范围分别是-1.35°~5.88°和-6.05°~0.86°;ED和DF、E’D’和D’F’在-4.98°~5.79°和-10.42°~4.23°变化,说明同侧的两个夹角同增减(变化量同号),异侧相反(变化量反号);两侧的连接臂和YOKE夹角变化量基本相同,而右侧的MSS和连接臂夹角约为左侧的2倍。
4 结论
(1)单点系泊状态下的平台在船舶侧向垂直撞击过程中,碰撞强度、作用时间及极限撞深均显著增加,舷侧结构的能量吸收比率也相应提高。
(2)系泊系统的约束作用对平台的运动响应有较大影响:横荡速度和位移显著增加,但整体偏转幅度降低(即艏尾位移减小);出现垂荡位移,碰撞过程由二维扩展到了三维,并且在该方向上平台振动明显,速度波动较大;在系泊系统提供的回复力作用下,横摇和艏摇的角速度和角度幅值降低,沿近似正弦曲线变化。

图13 YOKE与连接臂铰点D、D’路径投影图Fig.13 The projected paths of points D and D’
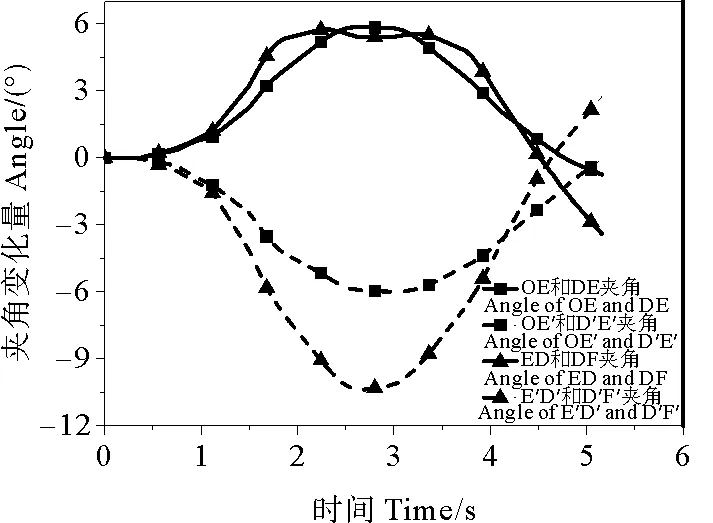
图14 系泊系统各部分夹角变化量时程曲线Fig.14 Time history curves of angle in mooring system
(3)系泊系统左右两侧的运动情况差异较大,应分开考虑。YOKE的两臂在不同的竖直平面内做圆周运动,在竖直方向运动最剧烈。连接臂在三维空间做复杂的曲线运动,其左右两侧沿船长方向交替错动,控制平台的艏摇角度。
