青岛港日最大降水量及其出现日期的联合统计分析❋
2019-01-04高俊国翟金金
高俊国, 翟金金, 董 胜
(中国海洋大学工程学院, 山东 青岛266100)
青岛地处北温带季风区域,受来自洋面上的东南季风及海流、水团的影响,空气湿润,年降水量充沛。降水对青岛港口营运影响很大,尤其是夏季的降雨。由于降雨停工、天晴突击装卸,加重了港口生产和船舶运行的不均衡性,降低了港航效益。为了加强青岛港口的营运水平,提高港口的通过能力,有必要对青岛地区历年日最大降水量及其出现日期和历年各月日最大降水量及其出现日期进行深入研究。
迄今,专家学者对降雨量的极值估计进行了研究:陈创买等[1]采用Gumbel分布和指数分布对广东省日最大降雨量重现期进行了计算。林巧美等[2]利用指数分布对揭阳市日最大降雨量和月最大降雨量进行拟合,分析降雨量的年际演变特征及月际变化,进而计算在不同重现期的极值。Cho等[3]利用Gamma分布和对数正态分布对卫星得到的降雨率数据拟合,比较得知对数正态分布的结果更优。Olofintoye等[4]选用Gumbel、对数正态、正态、对数-Gumbel、皮尔逊和对数皮尔逊分布对Nigeria地区的日最大降雨量特征进行描述,检验结果表明对数皮尔逊分布的拟合最优。石先武等[5]以温州站为例,利用5种极值模型模拟了台风降水概率,结果表明Weibull分布的整体拟合效果最佳。
降雨作为一种常见的水文事件,可以用降雨量、降雨天数和降雨强度等相互关联的特征量来描述[6]。而传统的单变量分布只能描述单一降雨指标的概率变化特征,多变量联合分布对研究降雨的综合统计特征有重要意义。Yue[7]采用两变量正态模型描述降雨特征量的联合分布,实现非正态变量的正态化;Yue[8]采用二维Gumbel逻辑模型分析降雨峰值和降雨总量的联合分布。以上成果要求对随机变量进行一定的假设,Copula函数的出现克服了这些局限,Salvadori[9]运用二维Frank Copula函数模拟降雨历时和降雨强度的联合概率分布,推求联合重现期等值线,引入第二重现期的概念,为风险评价提供科学依据。Lennartsson等[10]采用二维Gaussian Copula函数表征连续天数降雨之间的相关关系,结合马尔科夫链,构建了瑞典地区的降雨模型。Kao和Govindaraju[11]基于Plackett Copula函数构造降雨量、历时和峰值强度的二维和三维联合分布模型,并与Frank Copula函数建立的降雨模型进行对比,得出Plackett Copula函数可以克服Frank Copula不能描述相关性偏低的随机变量和难以构造高维联合分布的缺点,能够更全面地分析降雨特性。Zhang和Singh采用了三维Gumbel-Hougaard Copula函数建立了降雨历时、降雨强度和雨深的三维联合分布,计算了降雨事件的重现期[12]。Grimaldi和Serinaldi[13]采用7种三维Copula函数,建立了最大降雨强度、总降雨深和临界雨深的联合分布,确定了在已知重现期和临界雨深时的总降雨深和最大降雨强度。Bardossy和Pegram[14]运用非对称Copula函数描述降雨量及其发生的内在相关性,建立了多站降雨量的随机模型。Copula函数在降雨事件中得到了广泛的应用。
对于青岛地区降水的研究,多数集中在降水变化[15]以及日/月最大降水量的概率统计分析[16]上,缺乏对日最大降水量及其最可能出现日期(以下简称出现日期)的研究,而对于给定联合重现期,且日最大降水量给定某一重现值时,能确定该值在一年中(或某个月份中)的可能发生时间,能够有效地避开灾害风险,为提高港口的营运水平,扩大港口的通过能力有重要意义。因此,本文针对青岛地区近30 a的历年日最大降水量(RY)及其出现日期(LY),以及各月的日最大降水量(RM)及其出现日期(LM),基于Copula函数,分别建立二维联合分布模型,对(RY,LY)和各月(RM,LM)进行了分析讨论,得到对工程有意义的结论。
1 二维统计模型的构建
Copula函数是多个定义在[0,1]区间上均匀分布变量的联合概率分布函数,它可以描述多维边缘间的统计关系[9]。基于Sklar定理,若F(x,y)是边缘分布为FX(x)和FY(y)的二维联合分布函数,则必然存在一个二维Copula函数C(u,v)满足对任意的(x,y) ([-∞, +∞]2,有[17-19]
F(x,y)=C(u,v)=C(FX(x),FY(y))。
(1)
若FX(x)和FY(y)连续,则C(u,v)唯一;否则,C(u,v)由RanFX(RanFY唯一确定(Ran表示值域)。反之,若C(u,v)为二维Copula函数,u=FX(x)和v=FY(y)为边缘分布,则由式(1)确定的函数F(x,y)即为X和Y的二维联合分布函数[18]。
Copula函数主要分为椭圆型Copula和Archimedes Copulas等。其中,椭圆型Copula中的Gaussian Copula函数与常用的Nataf变换一致,其分布函数C(u,v)为[20]

(2)
式中:Φ(x)为标准正态分布的分布函数,Φ-1(x)为其逆;-1≤θ≤ 1为Φ-1(U)和Φ-1(V)的线性相关系数。θ= 0时,U和V独立;|θ| = 1时,U和V完全相关。
Archimedean Copulas由其生成元确定的单参数函数,是目前水文统计中运用较为广泛的一类Copula函数。其中,最常用的二维Archimedean Copula主要有以下几种[20-21]:

式中:u=FX(x)和v=FY(y)为边缘分布;θ为Copula函数的待定参数。
联合分布的参数估计分为两步[19,21]:第1步,根据日最大降水量(RY,RM)及其出现日期(LY,LM)的观测值序列,采用单变量分布的参数估计方法估计边缘分布u和v的参数;第2步,采用极大似然法估计Copula函数的参数[22-23]。
2 历年日最大降水量与出现日期的联合统计分析
2.1 历年日最大降水量及其出现日期的边缘分布
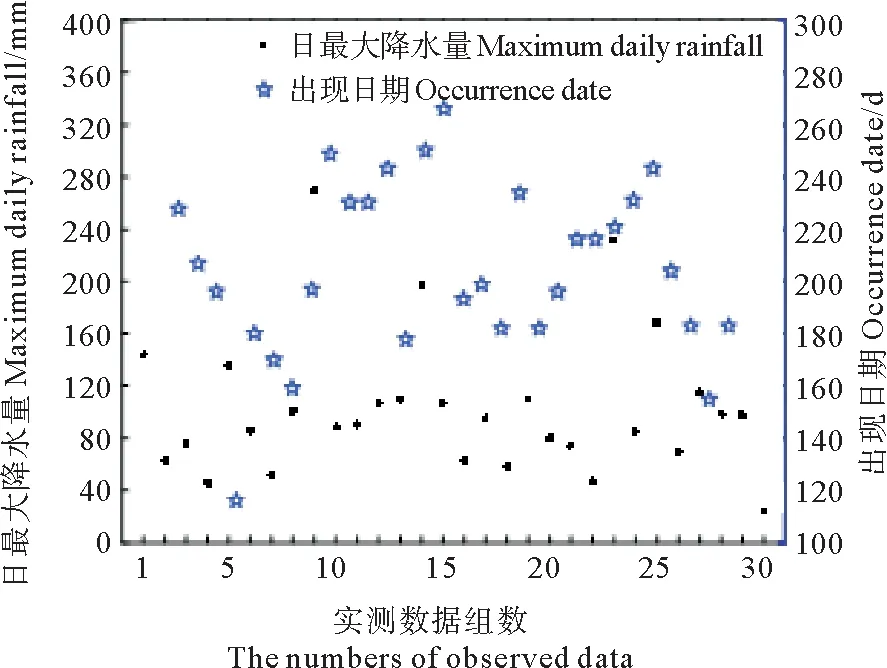
青岛地区历年日最大降水量(Maximum daily rainfall:RY)与其在该年中的出现日期(Occurrence date:LY)的散点图见图1,其中LY指日最大降水量RY在该年中发生时,从1月1日开始累加到该天的总天数。采用Pearson-Ⅲ型分布[24-25]和最大熵分布[26-27]分别拟合日最大降水量及其出现日期的边缘分布,
P-Ⅲ型分布的概率密度函数为

(7)
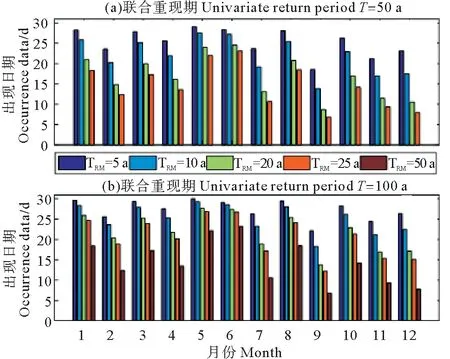
式中:a0为位置参数,且0 最大熵分布的概率密度函数为 (8) 式中:a0> 0为位置参数;β、γ与ε为待定参数。 首先采用式(7)对日最大降水量及其出现日期序列进行Kolmogorov-Smirnov检验(以下简称K-S检验) (9) 图1 青岛地区RY和LY的散点图Fig.1 The scatter plots ofRYandLY 经过计算,历年日最大降水量及其出现日期的K-S检验统计量DRY=0.130 4和DLY=0.097 7均小于D30(0.05)=0.241 7,说明所选取的分布均可以拟合日最大降水量及其出现日期序列(见图2),并分别推算给定重现期时日最大降水量及其出现日期的重现值(见表1)。 日最大降水量及其出现日期分别采用Pearson-Ⅲ型分布和最大熵分布作为边缘分布,基于二维Clayton Copula、Frank Copula、G-H Copula和Gaussian Copula函数,建立历年日最大降水量(RY)及其出现日期(LY)的二维概率模型,采用Pearson’s χ2检验对4种Copula函数进行假设检验,其检验统计量M的估计值为[28-29] (10) 图2 日最大降水量及其出现日期的拟合分布Fig.2 The fitting distribution forRYandLY 重现期 Return period/a510202550100日最大降水量Maximum daily rainfall RY/mm138168196205232258出现日期Occurrence date LY/d233248260263272281 表2 Copulas函数的假设检验和拟合优度评价Table 2 Hypothesis testing and goodness-of-fit evaluation of Copulas 将4种Copula函数计算得到的理论联合概率分布和经验联合联合概率分别点绘在图中(见图3),从图中可以看出,数据点均分布在45°线附近,可以直观地看出4种Copula函数拟合效果均较好。为了获得最优的拟合分布函数,结合均方根误差法(RMSE)选择一种Copula函数: 图3 二维Copulas拟合优度评价Fig.3 Goodness-of-fit test of bivariate Copulas (11) 式中:n为样本容量;F为理论分布计算值;P为经验概率。RMSE越小,说明该Copula函数拟合的越好。 根据表2的拟合优度评价,选取RMSE最小的Frank Copula函数作为联合概率分布的连结函数,其计算得到的联合重现期(RY和LY同时发生大于某阈值时联合概率的倒数)等值线见图4。 (点为历年日最大降水量及其出现日期的组合。Points denote the combinations ofRYandLY.) 图4 日最大降水量及其出现日期的联合重现期 由等值线(见图4)可知,当联合重现期为某个值时,有无数组RY和LY与其对应。此时给定一个日最大降水量,就可以得到该降水量相应所处该年的确切位置。文中给出了当联合重现期分别为50和100年时,日最大降水量取5、10、20、25年一遇的重现值时的出现日期,具体结果见表3。 表3 (RY,LY)联合重现期为50 a或100 a条件下,RY取不同重现值时的出现日期LYTable 3 LYcorresponding to a given univariate return valueRYunder joint return period (50 a or 100 a) of (RY,LY) 历年各月日最大降水量及其在该月中的出现日期分别为RMi和LMi(i=1~12),选取拟合较优的Pearson-Ⅲ型分布和最大熵分布分别拟合12个样本的日最大降水量及其出现日期的边缘分布,然后基于第2节中的4种二维Copula函数,建立联合概率分布模型,通过Pearson′s χ2假设检验和拟合优度评价(RMSE),均选取Frank Copula函数构建历年各月日最大降水量及其在该月中的出现日期的二维联合概率分布模型。 表4 (RMi,LMi)联合重现期为50、100 a,RMi取单因素重现值时对应该月的出现日期Table 4 LMifor different joint return period: 50、100 a when theRMiis the given univariate return value 图5 日最大降水量及其出现日期的边缘拟合分布图和联合重现期等值线图Fig.5 Marginal fitting distributions and joint return period contours of maximum daily rainfall and the associate occurrence date 由于篇幅的限制,文中仅给出春夏秋冬四个季节各一个月结果,RMi和LMi的边缘拟合分布和联合重现期等值线如图5。由等值线图可见,当联合重现期为某个值时,有无数组RMi和LMi与其对应。此时给定一个日最大降水量,就可以得到该降水量在该月的出现日期(见表4),其结果对避开降水大值区,合理安排港口作业时间,避免怠工损失具有十分重要的参考价值。 图6给出了当联合重现期分别为50和100 a时,历年各月日最大降水量取重现期为5、10、20、25、50 a的重现值时所对应的其在该月的出现日期。 图6 给定日最大降水量时,不同联合重现期下的出现日期(12个月)Fig.6 LMifor different joint return periodswhenRMis the given univariate return value (12 months) 收集青岛地区近30年的日最大降水量与其在该年中的出现日期,以及各月的日最大降水量及其在该月中的出现日期,共计13个样本序列为例,通过构建二维联合分布模型进行统计分析,得到如下结论: (1)针对青岛地区历年日最大降水量(RY)与其在该年中的出现日期(LY),以及各月的日最大降水量(RM)及其在该月中的出现日期(LM),分别建立了基于4种二维Copula函数(Clayton、Frank、Gumbel-Hougaard和Gaussian)的二维联合分布模型,根据拟合优度检验,二维Frank Copula联合分布模型最佳。 (2)通过二维联合分布模型,对日最大降水量(RY)与其在该年中的出现日期(LY)的相关关系以及各月的日最大降水量(RM)与其在该月中的出现日期(LM)相关关系进行研究,当联合重现期取定,且日最大降水量给定某一重现值时,可以估计该值在一年中(或某个月份中)的最可能出现的日期,因此能够有效地避开降水大值区,选择其他时段完成任务,从而为港口施工、建设和营运提供指导性建议,为防范极端气象情况做出合理、充分的准备。
2.2 历年日最大降水量及其出现日期的联合分布
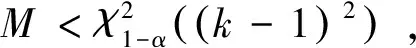
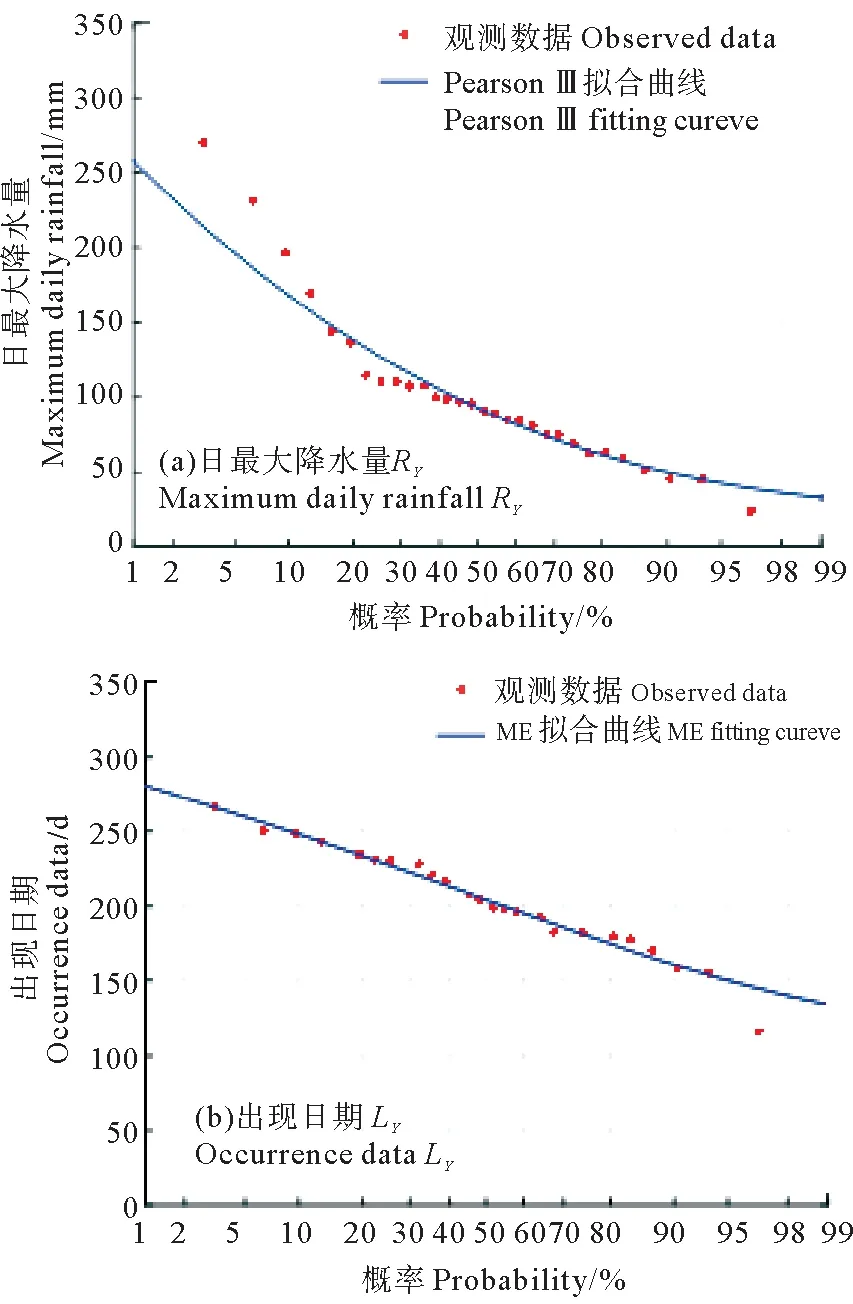
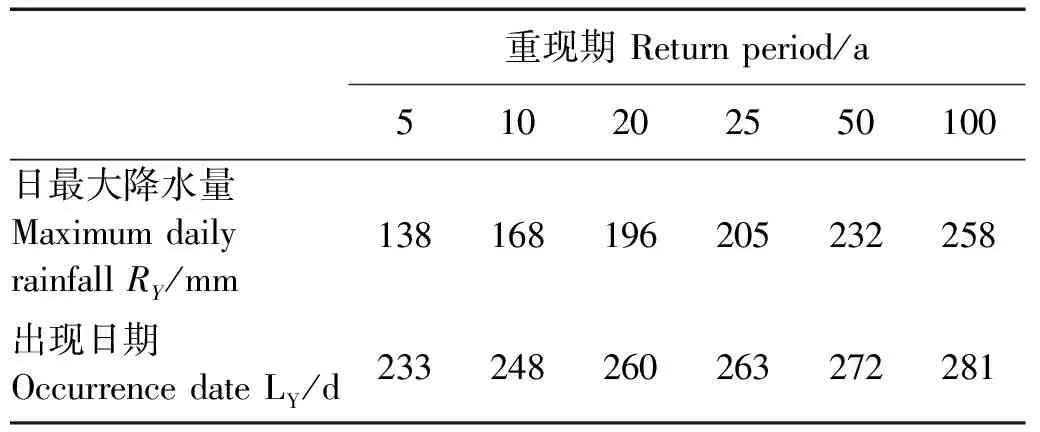
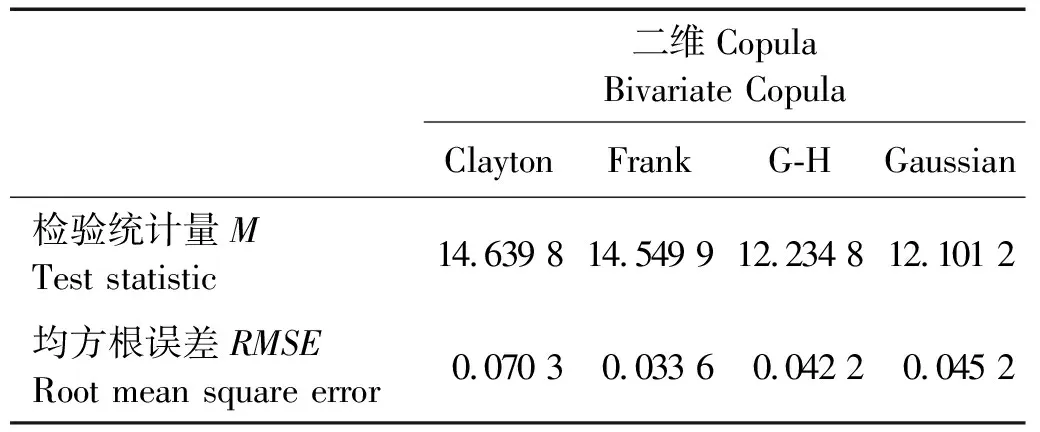

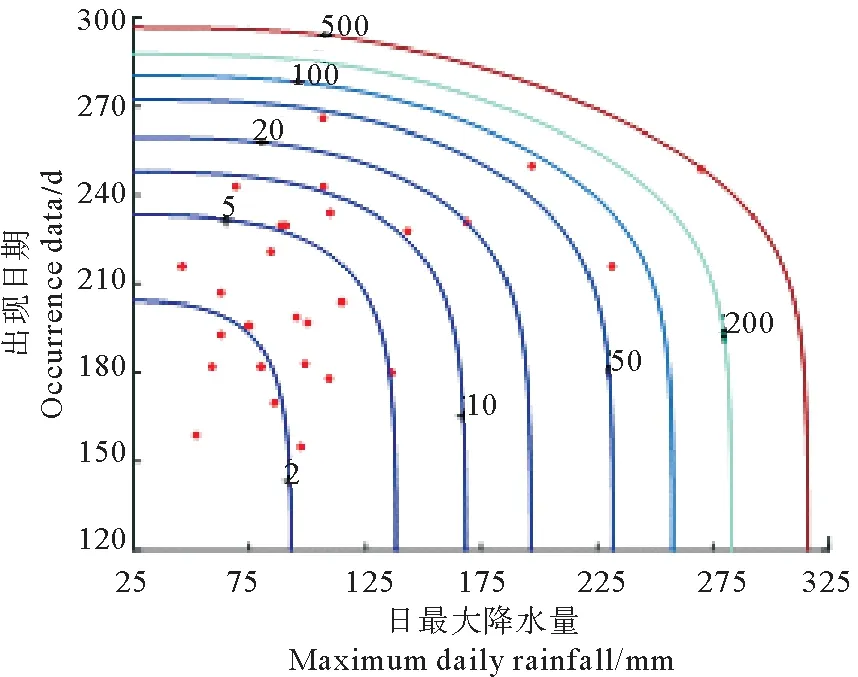
Fig.4 Joint return periods ofRYandLY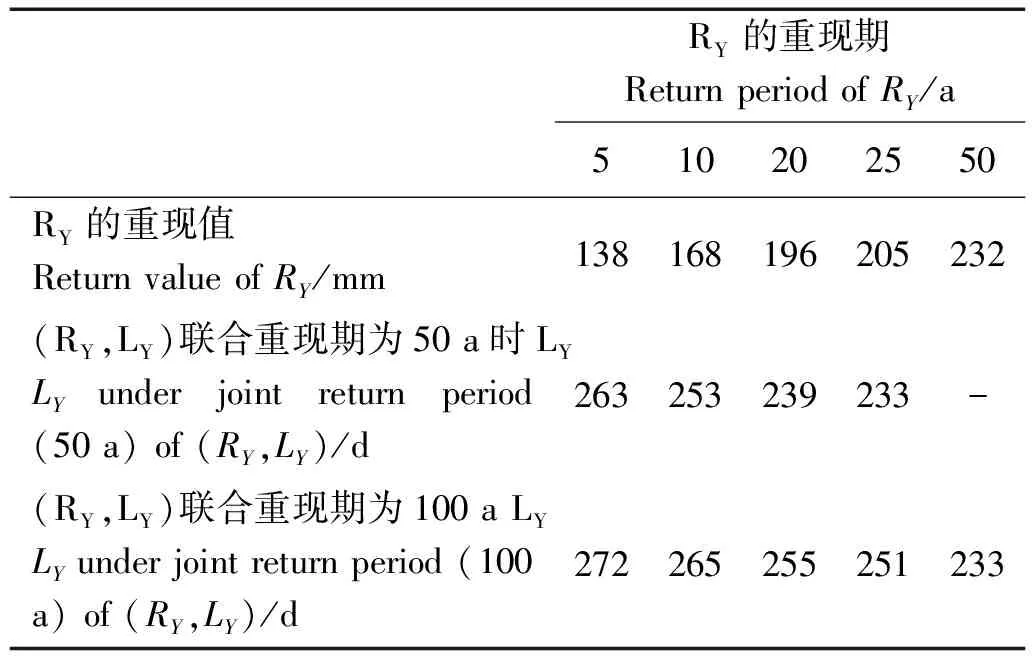
3 历年各月的日最大降水量及出现日期的统计分析


4 结论
