基于自适应滑模控制的分数阶蔡氏电路系统动力学分析与控制

朱 伟，陈 坤，王 谦，朱弘钊

(1.国网湖南省输电检修分公司，湖南 衡阳 421000；2.国网电力科学研究院武汉南瑞有限责任公司，武汉 430074； 3.电网雷击风险预防湖北省重点实验室，武汉 430074)

0 引 言

随着新能源汽车、无人飞行器(UAV)和平衡车的兴起，工业控制对象变得越来越复杂，控制精度的要求越来越高，因此对非线性动力系统控制的研究变得越来越重要。

非线性动力系统在电力，生物工程，金融等行业都具有广泛的应用，如电路系统，基因系统，金融系统等都与其动力学行为密切相关，我们的世界是由无数复杂的系统构成的，它们的状态直接影响着人民的生活、国家的稳定，甚至是整个世界的发展。例如，金融系统的不稳定性会导致金融危机，这对国家和人民都具有严重的危害。再如，电力系统的不稳定，可能会导致一些地区甚至全国范围内大面积停电，严重阻碍生产力发展，甚至造成巨大损失。再比如生态系统变得不稳定，可能会导致大量的生物繁殖，严重破坏生物圈的平衡，给人类社会造成不可估量的损失。因此，研究复杂系统的动力学过程，并试图控制它们以达到理想的状态是非常有价值和实际意义的。

在非线性动力系统中，蔡氏电路系统凭借着它独特的优势，在非线性发展的初期就已经占有了优势。早在1983年，蔡少棠教授研发出了蔡氏电路[1-3]，此研究结果在电子学界是一个重大的突破，同时也震惊了电子学界。

然而，对于它的研究，至今以来也是一个热点课题。一些学者是对蔡氏电路的复杂行为进行解释，一些研究者是针对如何控制蔡氏电路的复杂行为进行研究，其余的一些研究者们主要研究的难题是蔡氏电路的复杂行为的应用[4-5]。

然而，无论从哪一个研究方向来看，以前的研究人员们都主要是对一些全局蔡氏电路进行研究分析，对于分段的的蔡氏电路的研究非常的缺少[6-7]。最主要的原因是分段蔡氏电路相比于全局蔡氏电路的动力学特征，拥有更为复杂的表现形式。因此，对于蔡氏电路系统中分段蔡氏电路的研究要进一步的加强[8-9]。

此外，对于整数阶系统动力学行为的研究，国内外学者已经做了大量的工作，并且得到了许多重要结论。然而在实际生活中，主要存在着非整数阶。因此，研究分数阶混沌系统的动力学行为已经是目前非线性研究领域的一个重点方向[10-13]。因此本文主要针对于分数阶的蔡氏电路系统进行研究。

1 准备知识

本文中我们主要运用Caputo分数阶导数，因为Caputo分数阶导数的微分方程的初始条件与整数阶的初始条件是相同的，这样就能够在相同的条件下充分突出分数阶微积分的优越性[14-15]。

(1)

注意，我们使用CDα的简化形式Dα，考虑到分数只局限于α∈(0,1]范围内的情况，这里Γ(x)函数表示如下

(2)

它具有如下属性。

Γ(x+1)=xΓ(x)=x!

(3)

然后我们给出蔡氏电路的结构图

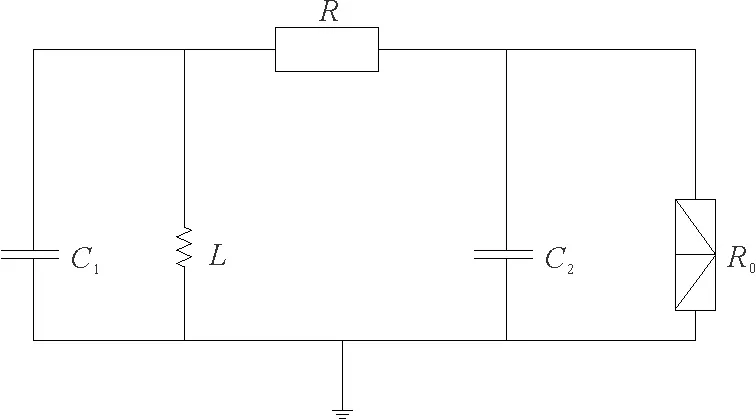
图1 蔡氏电路系统图Fig.1 Chua′s circuit system diagram

如图1所示，L是一个线性电感，R是一个可调电阻，C1,C2为两个线性电容，R0为一个非线性负电阻UC1,UC2为线性电容C1,C2的两端的电压，G是可调节的电阻R的电导，iRN是非线性电阻R0的电流，线性电感上的电流是iL，根据基尔霍夫电流定律，可得到系统的状态分数阶微分方程组

C1DαuC1=G(uC2-uC1)-g(uC1)
C2DαuC2=G(uC1-uC2)+iL
LDαiL=-uC2

(4)

2 稳定性分析

首先我们对系统进行无量纲化处理，令

则可以得到

(5)

这里

根据计算，可以得到系统的平衡点的分布如下

进行线性化处理之后，得到系统的特征方程矩阵为

(6)

之后我们得到

λ3α+A1λ2α+A2λα+A3=0

(7)

这里

定理1如果分数阶蔡氏电路系统的系数满足下列不等式组，那么该系统就会呈现渐近稳定状态。

(8)

证明：从不等式组(3.4)我们可以得到如下的不等式

即A1>0,A2>0,A3<0根据分数阶劳斯-赫尔维兹判据[16]我们可以得到当该系统的所有系数满足定理所给出的条件时，系统呈现出渐近稳定状态。

由于该定理只为证明分数阶蔡氏电路系统渐近稳定性的充分条件，因此当系统不满足上述情况时，可能会呈现震荡状态，也可能会呈现稳定状态。

3 自适应滑模同步控制

在本节中，主要研究了应用了自适应滑模控制对分数阶蔡氏电路系统进行控制。根据系统的状态方程组，我们可以得到驱动系统的以下形式：

Dα1ζ(t)=ηζ(t)+f(ζ(t)),

(9)

这里

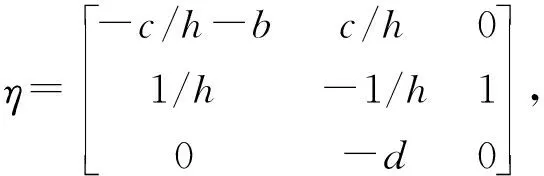
ζ(t)=,

加入自适应滑模控制器之后的响应系统为：

Dα1ζ(t)=φζ(t)+g(ζ(t))+u,

(10)

然后得到了误差函数的表达式

Dα1e(t)=φζ(t)-ηζ(t)+g(t)-f(t)+u,

(11)

然后我们选择分数阶蔡氏电路系统的滑模面为

(12)

求其微分为

(13)

为了提高分数阶蔡氏电路系统的鲁棒性和性能，我们定义了如下的自适应律

(14)

这里δ是自适应系数

定理2如果自适应滑模控制器的选取条件满足如下等式，那么就可以使得驱动系统和响应系统达到同步状态。

(15)

这意味着在任意初始条件下，我们选取满足上述式子的控制器，分数阶蔡氏电路的误差系统的各个状态变量总能够在该自适应滑模控制器下收敛到0，从而到达稳定状态。

证明：由于φ是一个常数矩阵，因此总是存在一个足够大的正整数ζ使得下列不等式成立0<φ<ζ

然后我们选取系统的正定能量函数为如下形式

(16)

这里θ为常数，令ξ*>ξ/κ,然后我们可以推导出能量函数的导数为

完成证明，从而推导出施加该自适应滑模控制器的分数阶蔡氏电路系统可以达到稳定状态。

由于本文首次通过自适应滑模控制对分数阶系统进行了控制并且获得了理想的结果，但本文只研究了分数阶算子从0到1的情况，对于其他的情况会在以后的研究中涉及。

同理，本文的目的旨在验证自适应滑模控制对一般的分数阶蔡氏电路系统是否具有有效性，对于特殊的情况，比如受到时间延迟，噪声以及扰动的影响的系统，我们将在以后的研究中去重点分析。

4 数值仿真

在这一节中，我们通过MATLAB将验证了分数阶蔡氏电路系统的稳定性和应用自适应滑模控制后系统的同步控制。

首先，根据定理1的条件，系统参数可以选择为a=0.34,b=-0.98,c=6.2,d=4.78,h=2.01。

分数阶算子选择为0.98，初值选取0.1，则系统(5)可写成如下形式

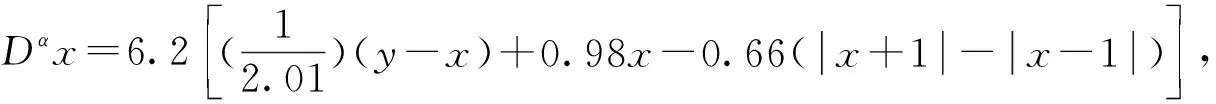
根据上述方程组我们可以得到下图的仿真结果。

从上图中可以清楚的得到，随着时间的推移，分数阶蔡氏电路系统中的各个变量都会逐步趋于稳定状态，即系统具有全局渐近稳定性。为了使得实验结果更加清楚，我们接下来给出相图的仿真结果。

图2 满足定理1的系统时序图Fig.2 The sequence diagram satisfying theorem 1

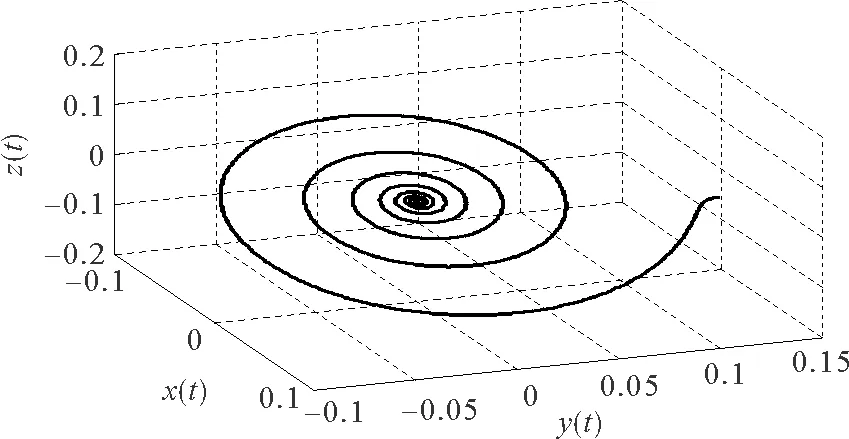
图3 满足定理1的系统相图Fig.3 The phase diagram satisfying theorem 1

从图3可以很直观地看出，图中具有一个明显的吸引子，系统最终会被该吸引子所吸引，从而使得系统收敛。

接着，我们选择不满足定理1并且使得系统不稳定的系数为a=-0.17,b=-1.68,c=5.5,d=1.78,h=1.01,分数阶算子和初值选取都不变，根据参数的选择我们得到了系统不稳定的时序图，如图4。然后选取满足定理2的自适应滑模控制器应用到该不稳定的分数阶蔡氏电路系统中，令自适应系数δ=0.34，从而得到了受到控制后的分数阶蔡氏电路系统的时序图如图5所示。

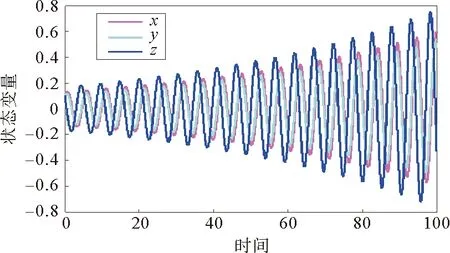
图4 不满足定理1的系统时序图Fig.4 The sequence diagram unsatisfying theorem 1

图5 应用自适应滑模控制的系统时序图Fig.5 Sequence diagram using adaptive sliding mode control

从图4中可以清楚的发现，当选择上述不满足定理1的参数时，分数阶蔡氏电路系统是呈现出不稳定状态的，而从图5中可以发现一旦对系统施加了满足定理2的自适应滑模控制器，系统就会逐渐趋于稳定状态。

为了更加清楚的表现出自适应滑模控制的有效性，接下来我们给出分数阶蔡氏电路系统中每一个变量在受到自适应滑模控制前后的对比时序图，如图6所示。

从图6中的a，b，c可以很明显的发现，系统在受到自适应滑模控制之后，振荡的幅度会逐渐的减小，随之逐渐趋于0，即系统达到稳定状态。由此可以得到自适应滑模控制对不稳定的分数阶蔡氏电路系统有良好的效果。下面我们在稳定后的一段时间内选择了一些时间点来分析自适应滑模控制的误差精度，见表1。

图6 应用自适应滑模控制前后的对比时序图Fig.6 Comparison sequence diagrams before and after applying adaptive sliding mode control

时间(秒)x(t)y(t)39.530.002 2390.001 52642.420.000 6180.000 52546.720.000 0230.000 01148.219.265e-0048.247e-00451.685.312e-0044.348e-00458.352.185e-0041.311e-00461.897.642e-0055.233e-00564.734.983e-0053.591e-00571.892.479e-0051.157e-00586.437.432e-0066.128e-00695.245.121e-0063.329e-0061003.523e-0061.921e-006

从表5.1可以看出，当系统达到稳定之后，各个变量的值随着时间的推移无限接近于0，误差极小。因此可以判断自适应滑模控制对分数阶蔡氏电路系统的控制具有相当高的精度和效率。

5 结论

在本文中，我们首先建立了分数阶蔡氏电路系统的微分方程模型。然后根据劳斯赫尔维兹判据推导除了分数阶蔡氏电路系统渐近稳定性的充分条件，从仿真图像上可以清晰的看到系统的各个参数如果满足所推导的充分条件，那么就会存在一个明显的吸引子，系统的运动被该吸引子吸引最后汇聚到一个中心点。

另一方面，我们将自适应滑模控制应用于分数阶蔡氏电路系统的不稳定状态。通过选择合适的分数阶滑模面和控制器来控制不稳定的系统达到稳定状态。仿真结果验证了自适应滑模控制方法的有效性和高精度高效率的优点。