基于二值的网络加速

谢佳砼

（西安市宇航中学，陕西西安，710038）

0 引言

卷积神经网络已经广泛运用与识别，模仿生物识别有较高的准确，最近深度学习的算法受到广泛关注，基于软件硬件的加速方法相继提出，软件算法中较为突出的为二值网络的加速，硬件FPFA的并行性得到了广泛的应用。

二值神经网络自从1943年提出以来，由于缺乏有效的从训练数据中学习网络系数的算法，而且相关理论的发展没有引起足够的关注，从而迅速被单精度神经网络迅速超越，未成为神经网络研究应用的主流，然而直至今日二值神经网络的使用价值被发现出来。在日新月异的现代社会里，科技日益更新换代，互联网信息的传输的速度显得格外重要，这时便少不了二值神经网络。

而二值卷积神经网络和普通的神经网路相比有什么样的优点或缺点呢？从优势上来讲，最大的一点就是其计算的简单性，相较于普通的神经网络，二值神经网络的运算简单性体现在网络中间值与网络参数的简单性，将浮点运算简化成为了整数计算，这无疑大大提升了其运算的速度，由于计算的量减少，所以其功耗也大大减少，这也其另一个优点。但是，二值神经网络的缺点也很明显，由于其算法将参数约束到+1和-1之间，所以其反在向传播中存在求导的问题，导致其预测准确率不够高，而这也是我们要解决的一个问题。用如何方式运算得到更高精度的深度卷积网络，成为了一大难题。

二值神经网络的发展和改进会大大的改造人类现在的生活情况，造福于社会生活，同时二值神经网络的原理十分新颖，走在时代的前沿，专家认为二值神经网络的发展会使完全的自动驾驶成为现实，其中二值神经网络的运输简便性则是信息快速运输的基础，从而进一步实现实时传递。同时，想通过前沿文献的阅读基本了解二值网络神经的运行机制，并且通过计算机的帮助进一步加深对二值神经网络的了解。

1 相关工作介绍

虽然深度卷积神经网络在许多计算机视觉任务中已经取得了相当好的性能，但是大的复杂的计算和参数大小阻碍了其在移动设备上的应用。 所以提出了各种方法来缓解这些问题：

（1）网络的修剪

从原理上来讲，神将网络的层数越多参数越多，最后所接受到的信息就会越精确，但是越精确也就意味着我们需要消耗更多的时间去进行计算，所以想要减少计算量就需要利用到网络修建技术，也就是把传递的信息中作用不大的信息给修剪掉，进而使得运算速率变快。若过多的参数会使得网络过拟合，训练起来过慢效果不佳，使得测试集误差过大，若过少的参数会使得网络无法训练，使得训练集误差无法缩减。选取合适的参数是一个很重要的问题，需要得到一个性价比最好的参数。

（2）网络的数据降维

在平时的生活中会利用计算机去处理一些复杂的问题，但是处理的文件越复杂其维度也就越高也就越难处理，所以数据降维也就是把数据的维度降低了，再进一步理解就是有用数据的保留和无关数据的丢弃，便于计算的可视化，其方法则是将高纬度的的数据特征映射到低维度再进行处理。选取合适的维度是一个重要的裁剪网络的方式，可以大大的降低网络的复杂度。

(3)哈希与神经网络

哈希算法是平时解决网络数据处理问题的一个重要的方法，而在这里又将哈希算法与神经网络加以结合，能够使神经网络的计算速度变快，将原来的浮点型权值映射到二值。哈希算法是一个映射，应用哈希映射在深度卷积网络是一个较为有效的方式。如何在网络中完成哈希运算是我们需要深思的问题。

2 二值卷积神经网络BNN

BNN在本节中我们详细介绍了二值化函数，以及我们如何用它来计算参数梯度，以及我们如何反向传播它。反向传播遇到了无法求导的问题，如何解决这个问题是一个我们需要解决的难点。

2.1 确定二值化和随机二值化

训练BNN时，我们将权值和激活值约束在+1和-1之间，从硬件角度来看，这两只是十分有利于计算的，所以，为了将变量转换称这两个值，我们使用了两种不同的二值化函数。

我们第一个使用的是确定性的

其中 Xb是二值化变量（权值或激活值），x是实值变量。它实现起来非常简单，并且在实践中运行得十分良好。

我们第二个使用的是随机性的：

其中σ是一个硬性的sigmoid函数：

随机二值化函数比符号函数更具吸引力，但实际上更难实现，因为它需要硬件在量化时生成随机的数值。 因此，我们主要使用确定性二值化函数（即符号函数）。

2.2 梯度计算和累积

虽然我们的训练是用二值化的权值和激活值来计算参数梯度的，但是根据确定性算法，在每次的参数计算后都需要权重的积累和更新。由于梯度具有累加效果，也就是说梯度是带有一定噪音的。所以通过在每个权重中累积的随机梯度贡献来平均噪声，多次累加梯度才能把噪音平均消耗掉。而且，二值化也就是给权值和激活值增添了噪声，而这样的量化噪声是能够很好的去调节权值，可以防止模型过拟合。我们训练BNN的方法可以看作是Dropout的一种变型，在计算参数梯度时，我们不是将激活值的一半随机设置为零，而是将激活和权重二值化，二值化则是将另一半变成1，所以可以看做是进一步的Dropout。

2.3 离散化梯度传播

由决定式算法我们可以看出，对其直接求导得出的值全部是零，很显然它对于反向传播来说很不合适，对于权值就无法进行一个更新，所以说我们引入了一个硬性的宽松函数，对Sign(x)函数进行一个宽松，这样我们就可以进行求导了。

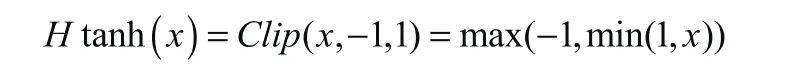
我们遵循类似的方法考虑到了符号函数的量化，并假设已获得梯度的估计量g，然后我们对于的估算就q会很简单。

即：

图1 sign(x)函数以及Htanh(x)函数

其中1|r|<=1的计算公式就是Htanh。

对于隐藏层，我们使用符号函数非线性来获得二值化的激活值，对于权重，我们将两个成分组合在一起：

W 投影到-1或1。 否则，权值会变得非常大，而不会对二值化的权重产生任何影响。

2.4 BNN的传递方式

再向前传递的过程中，我们先需要对权值进行一个二值化处理，处理之后，对二值化的权值进行一个伸缩处理，之后会得到一个中间值以及网络参数θ，最后对于中间量和参数进行归一化处理更新伸缩量。

再向后传递的过程中，因为我们之前把二值函数转化成为了一个可导的函数，所以我们要先求出其参数梯度，然后将参数梯度、中间量、网络系数三个值进行反归一化处理，就能够得到中间量和系数的导数，由于：

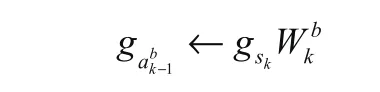
所以我们可以得到：

而在梯度参数的积累中，我们先利用网络的参数θ及其导数和学习值η去更新网络的参 数，进而的到所需的权值，最后再用一个λ去逐渐减少学习值η，进而达到信息反向传递的目的。

3 通过Hashing优化二值卷积神经网络

而h( x)和g( w)则是x和w的哈希函数，也就是说将x和w映射到+1和-1上，在之前曾经提到过：

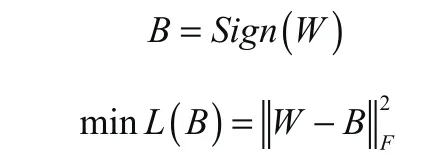
这是最原始的二值函数，也就是将二值的权重与哈希结合在了一起，但是在这里并不使用这个函数，而去借用哈希进行一个映射，而关于这个映射则需要使：

达到最小，在这里我受到了Rastegari的启发，引入了一个A，进而得到了：

其中A是对角矩阵， ai=Aii是Bi的缩放因子，最后我们的目标函数是：

由上一个公式我们又可以得到：

而在这里需要的是将αi看成常数，用这个公式去更新Bi，则令Z=α·X， q=α·XSi，且 T r()是一个求迹函数，代换后可以得到：

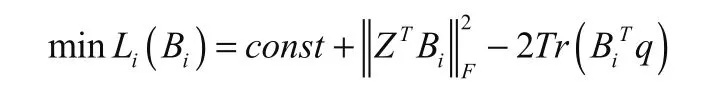
所以用这样的一个公式就可以很容易地进行求导，进而对Bi进行更新，那么对于α的更新也同样需要上面所说的函数对α进行更新，首先要对其求导：

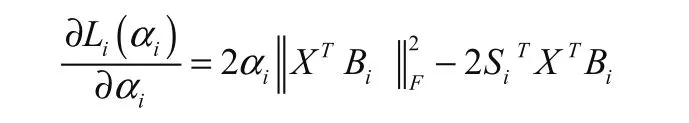
令其导数等于零，则得到：

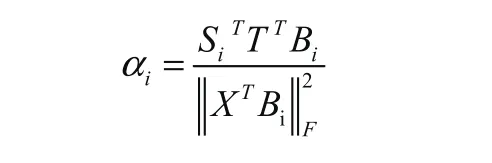
最后对α进行更新。

再回归到求最小值上，还是由于二值函数求导是没有办法算出参数梯度的，所以我又通过运用Shen等人在2015年所推导出的公式去进行一个最小值的运算：

在这个式子里Bi代表着在B这个矩阵中只有第i列在不断更新，而就是把Bi去掉后B中的所有数据， 而则是将Z的第j行给去掉后的所有数据，v就是Z的第j行，qj是q向量中的第j个元素。

若要取得最小值，就要使其乘积为负值，那么就得到了：

4 结论

本文从解决实际生活中因计算量过大无法进行实时传播，以及功耗过大导致其无法很好的运用到移动设备上，从而提出了二值化卷积神经网络，以及运用哈希映射简化了其运算的复杂程度，BNN大幅减少内存和访问所需的大小，并重新将大多数算术运算放在逐位运算中，这可能会使功耗大大降低，使得其在小的智能设备上使用，以及实时传递的实现。

可以在未来应用可以实时自动驾驶，以及监控拍摄，道路预测。