噪声参数传递标准件标准值的不确定度评定

田秀伟 楼红英 霍 晔 杨保国 段 飞 吴爱华

（1.中国电子科技集团公司第十三研究所，河北石家庄050051；2.中国电子科技集团公司第十四研究所，江苏南京210039；3.电子测试技术重点实验室，山东青岛266555）

1 引 言

噪声参数测量系统是低噪声放大器研制过程中必不可少的测量设备［1,2］，其测量结果的验证工作一直是业界的研究热点［3,4］。由于噪声参数测量系统的组成较为复杂，其计量验证方法一般依托噪声参数传递标准件（无源器件）。文献［5］报道了噪声参数测量系统的整体校准方法，文献［6］、［7］和［8］评估了噪声参数测量系统的测量能力，报道了测量结果不确定度的评定方法。文献［9］报道了噪声参数传递标准件标准值的计算方法。综上所述，对于计量工作中所用到的四个参数（测量值及其不确定度，标准值及其不确定度），只有标准值的不确定度还未见报道。

另一方面，现有系统生成商加拿大Focus公司和美国Maury公司也是依托无源器件（衰减器）进行噪声参数测量系统的性能验证，但是只是进行测量值与标准值的对比，并未给出相应的两种不确定度结果，这种现象给系统的计量带来较大困扰，因此急需开展噪声参数传递标准件的标准值的不确定度研究工作。

2 不确定度评定的测量模型

文献［9］报道了噪声参数传递标准件的标准值计算方法，决定噪声参数传递标准件标准值的主要物理量包括：噪声参数传递标准件的S参数，以及其所处的环境温度。文献［9］并没有给出噪声参数与上述两类物理量直接的数学关系，即没有明确不确定度的测量模型。为此，展开如下数学推导工作。

噪声参数传递标准件的噪声模型如图1所示，该模型的原理是将噪声参数传递标准件视为一个无噪声的网络，由传输参数T表征。CT1和CT2为输入端口两个本征噪声波。

传输参数与本征噪声的矩阵波如式（1）：

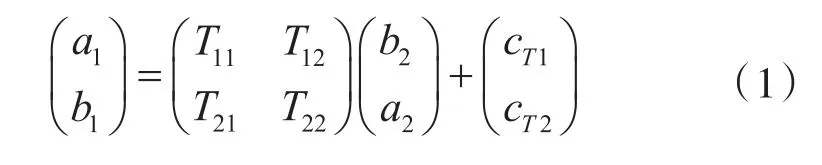
式中：a1,a2——端口的信号输入波；b1,b2——端口的信号反射波。

一般情况下，矢量噪声源由一个噪声相关矩阵表示，如式（2）：

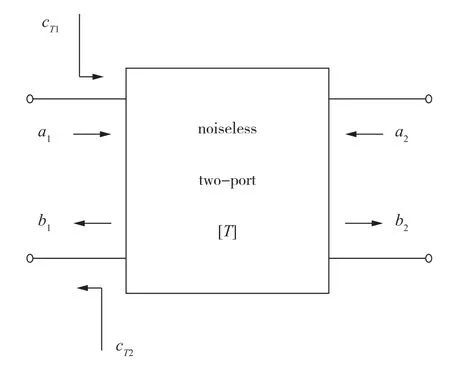
图1 噪声参数传递标准件的噪声模型Fig.1 Model of noise parameters standards

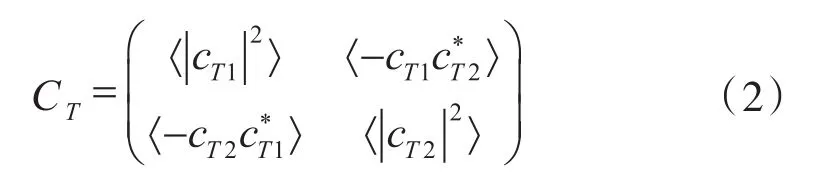
为了计算方便，我们进行如下定义：

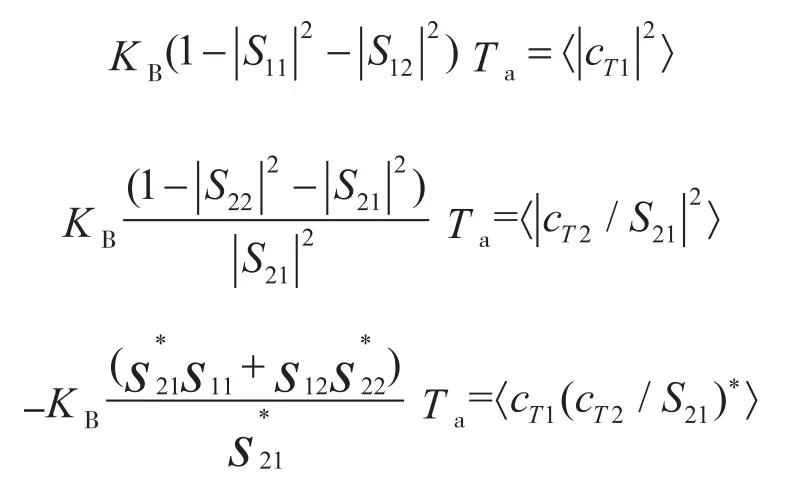
式中：KB——波尔兹曼常数；Ta——环境温度。

对于一个无源元件的线性两端口网络，其噪声主要由热噪声产生，根据Bosma's原理（假设热力学平衡情况下），其噪声相关矩阵为：

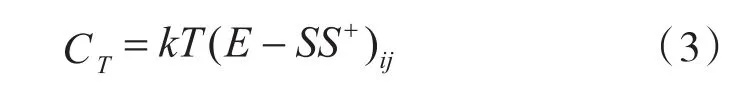
噪声相关矩阵与噪声参数的数学关系，如式（4）：

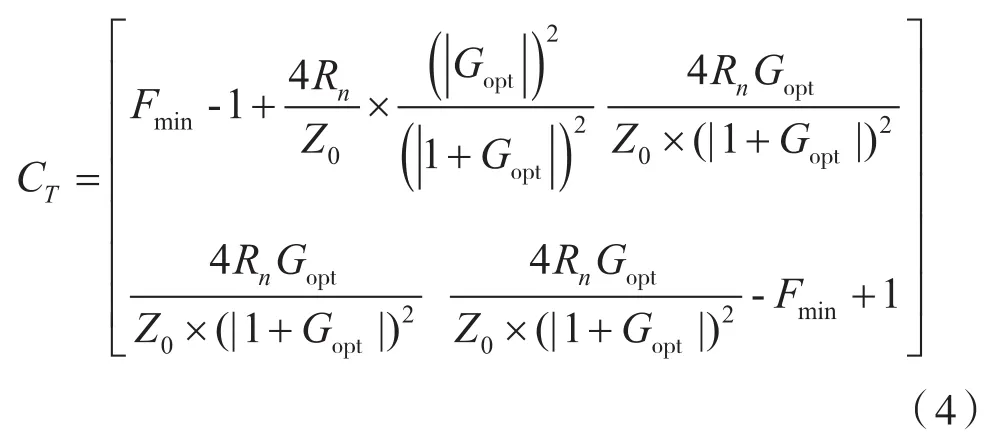
因此，可以得到噪声参数与S参数的数学关系，如式（5）～（7）所示：

其中，

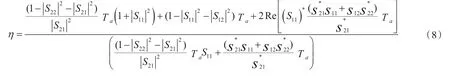
因此，式（5）～（7）即为无源器件S参数、环境温度与噪声参数的函数关系，即噪声参数传递标准件标准值的不确定度测量模型。

3 不确定度评定方法

采用传统的GUM不确定度评定方法，噪声参数传递标准件的不确定度评定，需依托测量模型求解四个噪声参数的偏导数。然而，因式（5）至式（7）中含有大量的复数参量，偏导数不易求解，甚至是无法求解偏导数（对于复数共轭的关系的物理量），因此通行的GUM方法不易评定噪声参数传递标准件标准值的不确定度。

为了克服上述困难，我们选择了JJF—1059.2推荐的蒙特卡洛法（简称MCM）。分析测量模型中的输入量为四个S参数和环境温度Ta（标准噪声温度T0为常量）。采用MCM方法，首要因素是分配输入量的概率分布，主要包括四个S参数的实部和虚部分别符合正态分布，环境温度Ta符合均匀分布。其次确定分布函数，我们采用的方法是：输入量的测量结果作为其期望的最佳估计值，输入量测量结果的标准不确定度作为其标准偏差的最佳估计值。最后使用MATLAB开发平台，将输入量概率密度函数通过测量模型传递，获得噪声参数传递标准件标准值的最佳估计值及不确定度，软件界面如图2所示。

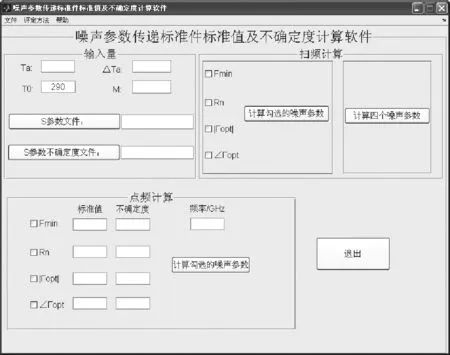
图2 噪声参数传递标准件标准值及不确定度计算软件主界面Fig.2 Software for calculating noise parameters standards'uncertainty

图2中，主工作区中主要包括输入量区域、扫频计算区域、点频计算区域。

输入量区域包括以下内容：

1）Ta：Ta为环境温度 （热力学温度），在空白处输入Ta值，单位为开尔文，单位符号为K；

2）T0：T0为标准噪声温度，一般设定为290K；

3）△Ta：△Ta为环境温度的波动量（热力学温度），在空白处输入△Ta值，单位为开尔文，单位符号为K；

4）M：M为蒙特卡洛仿真次数，根据需求在空白处输入仿真次数，参照JJF 1059.2—2012《用蒙特卡洛法评定测量不确定度》技术规范，建议仿真次数为100万次，从而保证提供95%的包含概率；

5）S参数文件：S参数文件为测试的S参数的数据，点击“S参数文件”按钮选择所需的S参数文件（后缀为.s2p的文件），文件名及路径显示在空白处；

6）S参数不确定度文件：S参数不确定度文件为测试的S参数相对应的不确定度的数据，点击“S参数不确定度文件”按钮选择所需的S参数不确定度文件（后缀为.xls和.xlsx的文件），文件名及路径显示在空白处。

扫频计算区域包括以下内容：

1）□Fmin：Fmin为全频段最小噪声系数，Fmin前面的□可点击选择；

2）□Rn：Rn为全频段等效噪声电阻，Rn前面的□可点击选择；

3）□ |Γopt|：|Γopt|为全频段最小噪声系数，|Γopt|前面的□可点击选择；

4）□∠Γopt：∠Γopt为全频段最小噪声系数，∠Γopt前面的□可点击选择；

5）计算勾选的噪声参数：选择上述1）～4）中需要的噪声生参数后，点击“计算勾选的噪声参数”按钮，计算完成后会生成“结果.xls”的EXCEL文件，Sheet1为噪声参数的标准值数据，Sheet2为噪声参数的不确定度数据，并生成相应的曲线；

6）计算四个噪声参数：与上述选择1）～4）噪声参数不同，点击“计算四个噪声参数”按钮计算四个噪声参数，计算完成后会生成“结果.xls”的EXCEL文件，Sheet1为四个噪声参数的标准值数据，Sheet2为四个噪声参数的不确定度数据，并生成相应的曲线。

点频计算区域包括以下内容：

1）频率/GHz：在频率/GHz下方空白处输入需要的频率点；

2）□Fmin：Fmin为单个频率点时最小噪声系数，Fmin前面的□可点击选择；

3）□Rn：Rn为单个频率点时等效噪声电阻，Rn前面的□可点击选择；

4）□ |Γopt|：|Γopt|为单个频率点时最小噪声系数，|Γopt|前面的□可点击选择；

5）□∠Γopt：∠Γopt为单个频率点时最小噪声系数，∠Γopt前面的□可点击选择；

6）计算勾选的噪声参数：选择上述2）～5）中需要的噪声生参数后，点击“计算勾选的噪声参数”按钮，计算完成后所选择的噪声参数的标准值和不确定度会出现在界面上并生成相应的噪声参数概率分布图。

以噪声参数传递标准件（衰减值：14dB）为计算对象，计算(1～40)GHz频带范围，噪声参数传递标准件最小噪声系数Fmin标准值不确定度结果如图3所示。

由图3可知，传递标准件Fmin的标准值的不确定度随着频率的上升，逐渐变大，量值范围为(0.01～0.6)dB，主要原因是S参数的不确定度随频率单调递增。在噪声参数测量系统计量时，采用该软件评定传递标准件的标准值不确定度，可以提高计量成效明确计量结果的可信度。

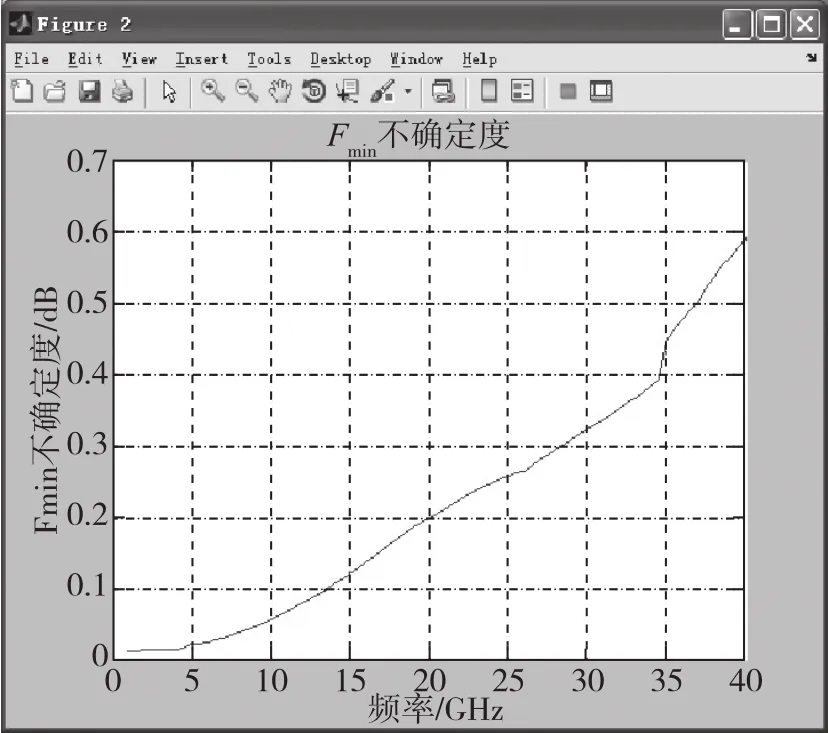
图3 Fmin不确定度计算结果Fig.3 Results for calculating Fmin uncertainty

4 试验数据及分析

为验证评定不确定度的合理有效，选择I型噪声参数传递标准件（衰减值：14dB，反射系数：0.55）进行试验数据分析，根据测得的S参数和S参数的不确定度，用软件计算得到四个噪声参数的标准值及不确定度与六次实际测试得到的测量值进行比较。结果如图4至图7所示。

综上分析，经过试验数据及分析验证，四个噪声参数的六次实际测试得到的测量值与软件计算得到的标准值的偏差值在(2～6)GHz频段均在不确定度的范围内，符合预期。

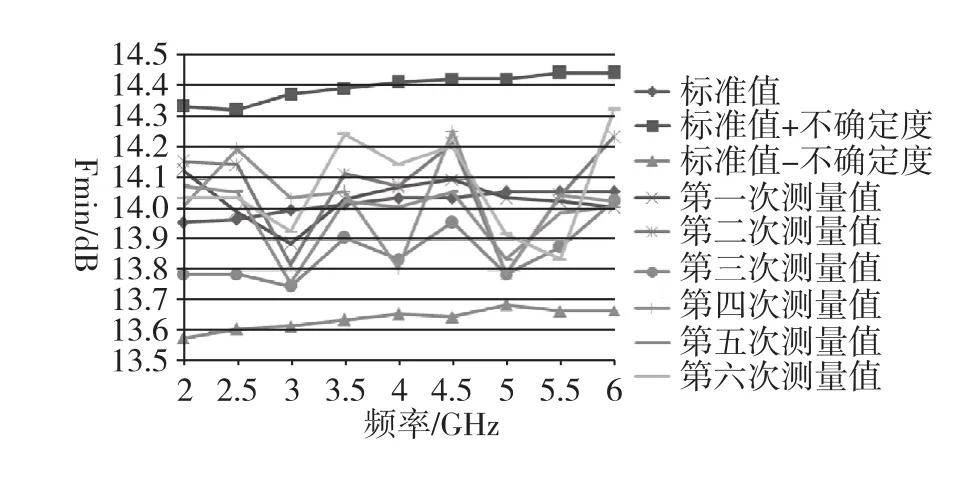
图4 Fmin标准值及不确定度与六次测量值结果比较Fig.4 Comparison between standard value and uncertainty of Fmin and sit measurements

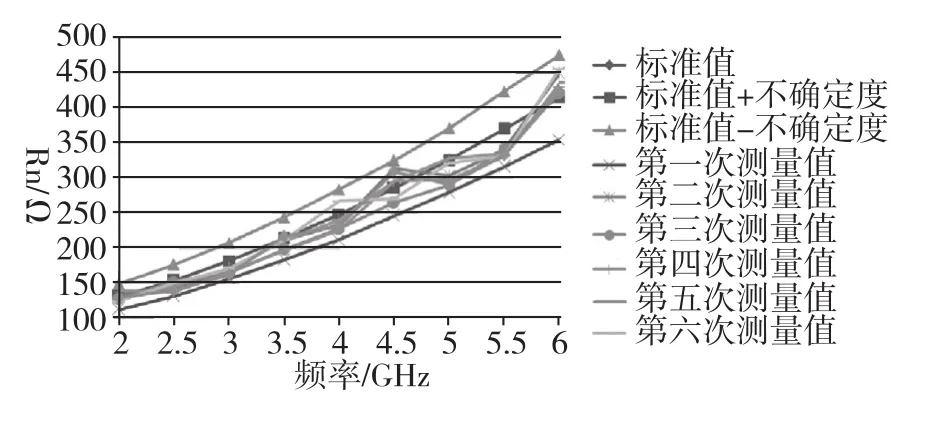
图5 Rn标准值及不确定度与六次测量值结果比较Fig.5 Comparison between the standard value and uncertainty of Rn and six measurements

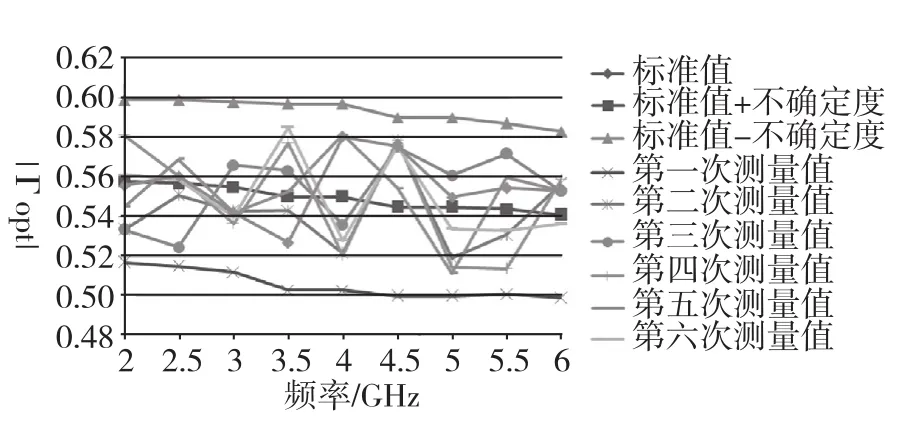
图6 |Γopt| 标准值及不确定度与六次测量值结果比较Fig.6 The comparison between the standard value and uncertaity of |Γopt| and six measurements

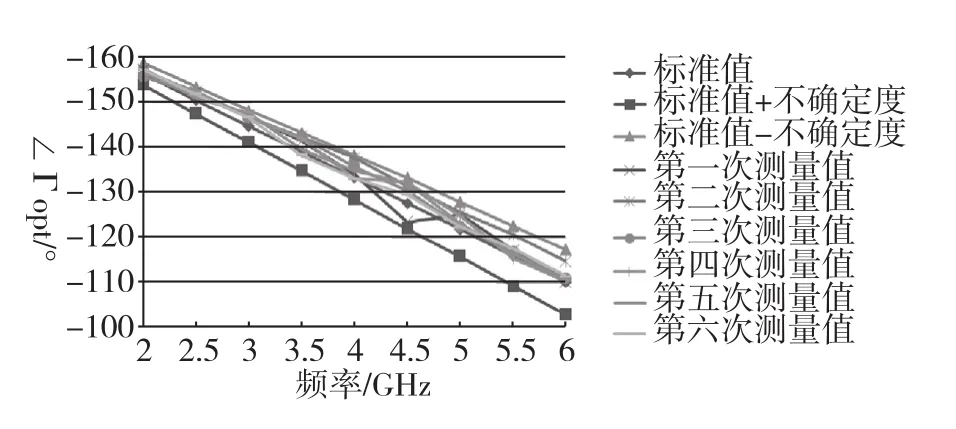
图7 ∠Γopt标准值及不确定度与六次测量值结果比较Fig.7 The comparison between the standard value and uncertaity of ∠ Γopt and six measurements

5 结束语

本文首次报道了噪声参数传递标准件标准值的不确定度评定方法，完善了噪声参数测量系统计量工作，解决了由于缺失标准值的不确定度所带来的计量结论判定难题。提出的不确定度评定方法，不仅推进了噪声参数测量系统的有效计量，而且推动了噪声参数数传递标准件的优化设计。