椭圆的“第三定义”——从课本上一道例题谈起

■河南师范大学附属中学

人教版教科书高中《数学》选修2-1第41页有这样一道例题:如图1,设点A、B的坐标分别为(-5,0),(5,0)。直线AM,BM相交于点M,且它们的斜率之积是,求点M的轨迹方程。

图1

对此例题推广到一般情况:设点A、B的坐标分别为(-a,0),(a,0)。若直线AM,BM相交于点M,且它们的斜率之积是-(a＞0,b＞0),求点M的轨迹方程。

椭圆的 “第三定义”:平面内与两个顶点连线的斜率之积为绝对值不为1的负实数的点的轨迹是椭圆。

根据椭圆的“第三定义”以及上面的证明过程我们不难得出:

不难发现结论1中线段AB是椭圆的长轴,是椭圆的一条特殊的直径(过椭圆中心的弦叫作椭圆的直径),对于椭圆一般的直径来说,同样的结论能否成立呢?

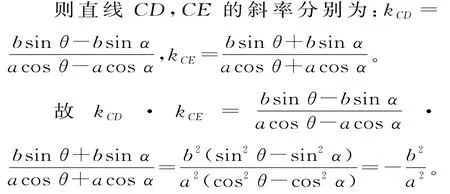
于是我们得到:

结论2中,显然O为直径DE的中点,于是在三角形CDE中就很容易想到构造三角形的中位线,如图3,设M为椭圆的弦CD的中点,则OM∥CE,当直线CD不垂直于坐标轴时,显然kOM=kCE,根据结论2我们不难得出椭圆中点弦的一条重要性质:

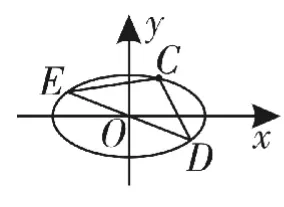
图2

图3

数学中很多知识是相互关联的,也是有规律可循的,多掌握一些有逻辑联系的数学结论,对我们数学解题是大有裨益的。下面针对本文介绍的结论,给出一些具体的题目供大家练习。

针对练习:

参考答案与提示:

同理可证,点P位于椭圆的下顶点时∠APB最大。