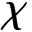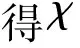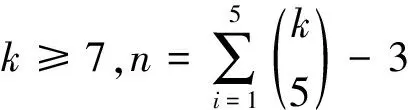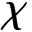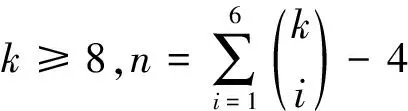两类完全二部图的一般点可区别全染色

苏 丽，陈祥恩，王治文

(1.西北师范大学数学与统计学院，甘肃 兰州 730070；2.宁夏大学数学计算机科学学院，宁夏 银川 750021)

0 引言

图的染色是图论研究中备受关注的一个课题.点可区别正常全染色在文献[1-2]中均有研究.文献[3-4]讨论了点可区别IE-全染色问题.点可区别一般全染色在文献[5]中被提出.

一个图G使用k种颜色1，2，…，k的一般全染色是指从V∪E到{1，2，…，k}的一个映射.一个图G的IE-全染色是指从V∪E到{1，2，…，k}的一个映射f，使得对任意相邻顶点u和v，f(u)≠f(v).

设f为G的一个一般全染色(或IE-全染色)，x为G的一个顶点，记C(x)={f(xu)|xu∈E}∪{f(xu)}，称之为顶点x在f下的色集合.设f为G的一般全染色(或IE-全染色)，若对u，v∈V，u≠v，总有C(u)≠C(v)，则f称为图G的点可区别一般全染色或者一般点可区别全染色(或点可区别IE-全染色)，简记为GVDTC(或VDIETC).令

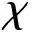
文献[6]研究了完全二部图K2，n及K3，n的一般点可区别全染色，确定了它们的一般点可区别全色数.本文将探讨完全二部图K4，n及K5，n的一般点可区别全染色.

2 预备知识

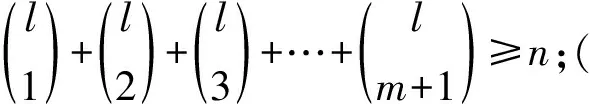
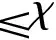
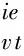
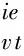
简单计算，得到如下引理1和引理2：

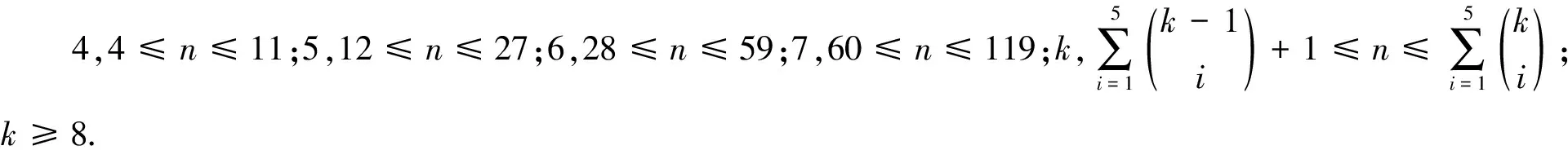
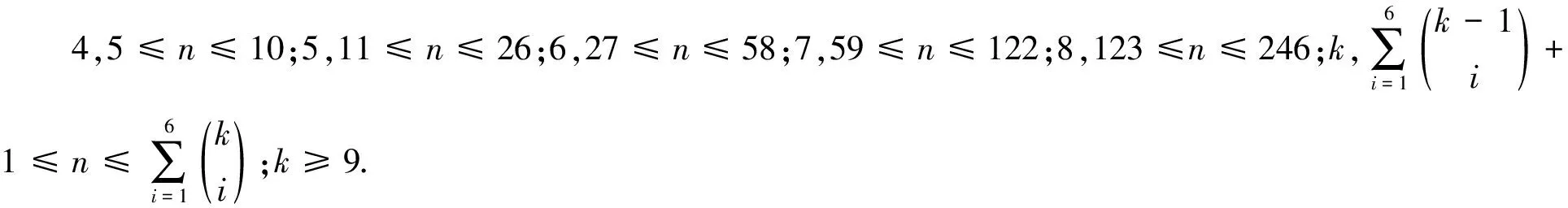
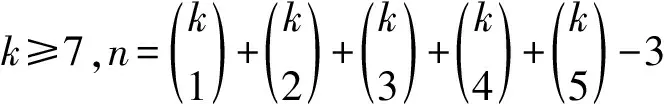
证明令D(x1)={1，2，3，…，k}，D(x2)={1，2，3，…，k-2，k-1}，D(x3)={1，2，3，…，k-2，k}，D(x4)={1，2，3，…，k-3，k-1，k}.将{1，2，3，…，k}的除{k}，{k-1}，{k-2}外的所有1-子集、2-子集、3-子集、4-子集和5-子集进行排序，使前k个子集分别为{1}，{2}，{3}，…，{k-3}，{1，k-2}，{1，k-1}，{1，k}.这样得到的序列共有n项，依次标记这n个子集为D(y1)，D(y2)，…，D(yn).如下构造K4，n的k-一般全染色：

(ⅰ) 当D(yi)={l}是1-子集时，用颜色l染点yi和它的关联边.

(ⅱ) 边x1yk-2，x2yk-2，x3yk-2染以k-2，而x4yk-2染以颜色1；边x1yk-1，x2yk-1，x4yk-1染以k-1，而x3yk-1染以1；边x1yk，x3yk，x4yk染以k，而x2yk染以1.

(ⅲ) 当D(yi)={l1，l2}(k+1≤i≤n)是2-子集时，用颜色min[D(yi)∩D(xj)]染边xjyi，j∈{2，3，4}；用D(yi)中没有染给边x2yi的颜色来染边x1yi和点yi.

(ⅳ) 当D(yi)={l1，l2，l3}是3-子集时，用颜色min[D(yi)∩D(xj)]染边xjyi，j∈{2，3，4}；用D(yi)中没有染给边x2yi的两种颜色分别来染边x1yi和点yi.

(ⅴ) 当D(yi)={l1，l2，l3，l4}是4-子集时，用颜色min[D(yi)∩D(x2)]=a染边x2yi，用颜色min{[D(yi){a}]∩D(x3)}=b染边x3yi，用颜色min[D(yi)∩D(x4)]染边x4yi，用D(yi){a，b}中的两种颜色分别来染边x1yi和点yi.

(ⅵ) 当D(yi)={l1，l2，l3，l4，l5}是5-子集时，用颜色min[D(yi)∩D(x2)]=s染边x2yi，用颜色min{[D(yi){s}]∩D(x3)}=t染边x3yi，用颜色min{[D(yi){s，t}]∩D(x4)}=p染边x4yi，用D(yi){s，t，p}中的两种颜色分别来染边x1yi和点yi.

(ⅶ) 用颜色k染点x1，x3，x4，用颜色k-1染点x2.

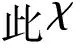
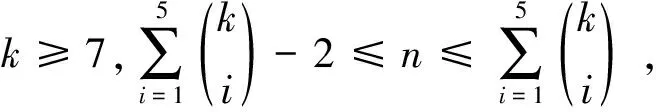
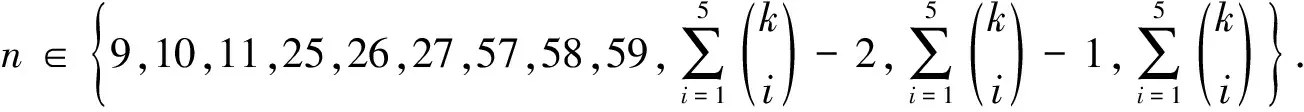
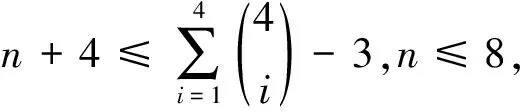
如果Y中至少有l-1个点的色集合是1-子集，不妨设Cg(yi)={i}，i=1，…，l-1，这将导致Cg(xi)⊇{1，…，l-1}，则Cg(xi)是{1，…，l-1}或{1，…，l-1，l}(i=1，4)矛盾.如果Y中恰有l-2个点的色集合是1-子集，不妨设Cg(yi)={i}，i=1，…，l-2，则Cg(xi)={1，…，l-1，l}，{1，…，l-1}，{1，…，l-2，l}，{1，…，l-3，l-2}，i=1，4，因此{1，…，l-3，l-2}必是X中某点的色集合.此时{l}，{l-1}，{l-1，l}都不是任一点的色集合，从而可类似得上面结果.

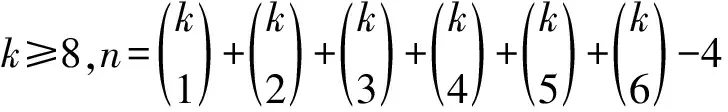
证明令D(x1)={1，…，k}，D(x2)={1，…，k-1}，D(x3)={1，…，k-2，k}，D(x4)={1，…，k-3，k-1，k}，D(x5)={1，…，k-4，k-2，k-1，k}.对{1，…，k}的除{k}，{k-1}，{k-2}，{k-3}外的所有1-子集、2-子集、3-子集、4-子集、5-子集和6-子集进行排序，前k个子集分别为{1}，…，{k-4}，{1，k-3}，{1，k-2}，{1，k-1}，{1，k}，得到的序列共有n个项，依次标记这n个子集为D(y1)，…，D(yn).下面构造K5，n的k-一般全染色.

(ⅰ) 当D(yi)={l}是1-子集时，用颜色l染点yi和它的关联边.

(ⅱ) 边x1yk-3，x2yk-3，x3yk-3，x4yk-3染以k-3，而x5yk-3染以min[D(x5)∩D(yk-3)]；边x1yk-2，x2yk-2，x3yk-2，x5yk-2染以k-2，而x4yk-2染以min[D(x4)∩D(yk-2)]；边x1yk-1，x2yk-1，x4yk-1，x5yk-1染以k-1，而x3yk-1染以min[D(x3)∩D(yk-1)]；边x1yk，x3yk，x4yk，x5yk染以k，而x2yk染以min[D(x2)∩D(yk)].

(ⅲ) 当D(yi)={l1，l2}(k+1≤i≤n)是2-子集时，用颜色min[D(yi)∩D(xj)]染边xjyi，j∈{2，3，4，5}；用D(yi)中没有染给边x2yi的颜色来染边x1yi和点yi.

(ⅳ) 当D(yi)={l1，l2，l3}是3-子集时，用颜色min[D(yi)∩D(xj)]染边xjyi，j∈{2，3，4，5}；用D(yi)中没有染给边x2yi的两种颜色来分别染边x1yi和点yi.

(ⅴ) 当D(yi)={l1，l2，l3，l4}是4-子集时，用颜色min[D(yi)∩D(x2)]=a染边x2yi，用颜色min{[D(yi){a}]∩D(x3)}=b染边x3yi，用颜色min[D(yi)∩D(x4)]染边x4yi，用颜色min[D(yi)∩D(x5)]染边x5yi，用D(yi){a，b}中的两种颜色分别来染边x1yi和点yi.

(ⅵ) 当D(yi)={l1，l2，l3，l4，l5}是5-子集时，用颜色min[D(yi)∩D(x2)]=s染边x2yi，用颜色min{[D(yi){s}]∩D(x3)}=t染边x3yi，用颜色min{[D(yi){s，t}]∩D(x4)}=p染边x4yi，用颜色min[D(yi)∩D(x5)]染边x5yi，用D(yi){s，t，p}中的两种颜色分别来染边x1yi和点yi.

(ⅶ) 当D(yi)={l1，…，l6}是6-子集时，用颜色min[D(yi)∩D(x2)]=d染边x2yi，用颜色min{[D(yi){d}]∩D(x3)}=e染边x3yi，用颜色min{[D(yi){d，e}]∩D(x4)}=f染边x4yi，用min{[D(yi){d，e，f}]∩D(x5)}=g染边x5yi，用D(yi){d，e，f，g}中的两种颜色分别染边x1yi和点yi.

(ⅷ) 用颜色k-3染点x1，用颜色k-1染点x2，用颜色k染点x3，x4，x5.

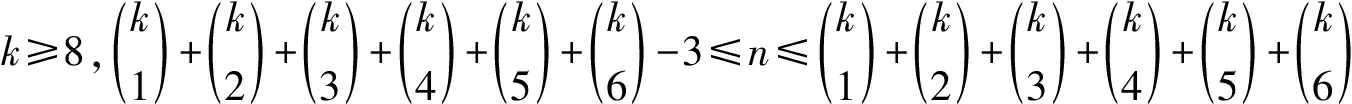
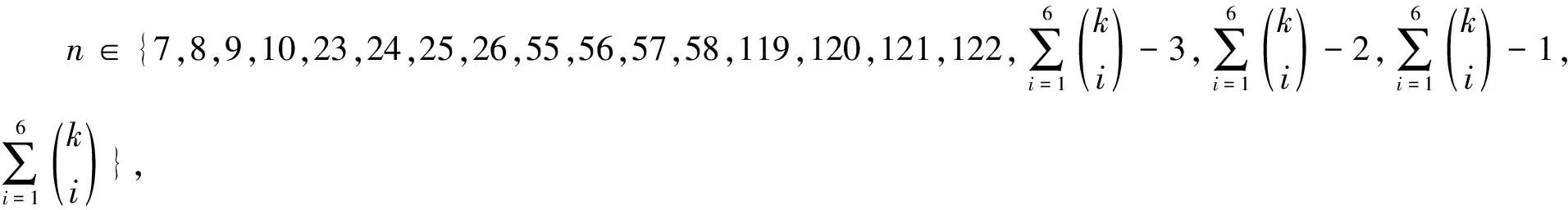
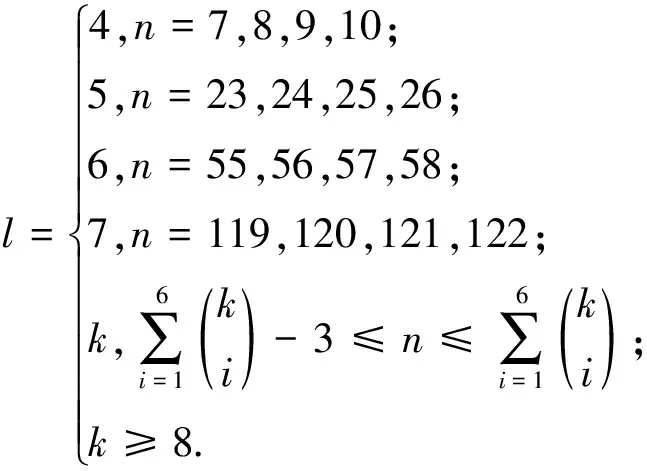
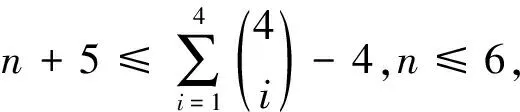
如果Y中至少有l-2个点的色集合是1-子集，不妨设Cg(yi)={i}，i=1，…，l-2，这将导致Cg(xi)⊇{1，…，l-2}，则Cg(xi)是{1，…，l-2}，{1，…，l-2，l-1}，{1，…，l-2，l}，{1，…，l-2，l-1，l}，i=1，4，5，矛盾.如果Y中恰有l-3个点的色集合是1-子集，不妨设Cg(yi)={i}，i=1，…，l-3，则Cg(xi)={1，…，l-1，l}，{1，…，l-1}，{1，…，l-2，l}，{1，…，l-3，l-1，l}.对于X中某点的色集合在此处还有四种可能出现的情况：{1，…，l-3，l-2}，{1，…，l-3，l-1}，{1，…，l-3，l}，{1，…，l-3}，i=1，4，5.此时{l}、{l-1}、{l-2}、{l-1，l}，或{l}、{l-1}、{l-2}、{l-2，l}，或{l}、{l-1}、{l-2}、{l-2，l-1}，或{l}、{l-1}、{l-2}、{l-2，l-1，l}不是任意点的色集合.经计算可得类似上面结果成立.

3 主要结果及其证明