基于Abaqus的杆密封结构密封性能分析及优化设计
2019-01-02徐时贤苏正涛
徐时贤,苏正涛
(1. 中国航发北京航空材料研究院,北京 100095;2. 中国航空发动机集团减振降噪材料及应用技术重点实验室,北京 100095)
改革开放以来,国内工程机械行业快速发展,要使工程机械充分发挥其技术效能,做好维修保养非常重要[1],而工程机械中液压技术广泛应用,密封性能严重制约液压技术的应用和工程机械的使用。如果发生漏油类的故障,不仅污染环境,而且影响执行元件的正常工作。目前,国内关键部位的密封件主要依赖进口,但是进口密封件通常价格昂贵、供货周期长、反应速度慢[2],因此,对密封件的材料和结构展开研究十分重要。
组合密封是比较先进的一种密封系统,它由橡胶材料和塑性密封圈材料两种材料构成,结构简图如图1所示。这种结构的组合密封用塑料做摩擦件,具有摩擦系数低的特点;用橡胶作弹性件,弹性优良,与一般橡胶密封圈密封不同的是橡胶不参与往复运动的摩擦,从而消除了橡胶作为摩擦件带来的种种弊端,同时橡胶材料作为不可压缩材料,可以对塑性密封圈的磨耗起补偿作用[3-5]。橡塑组合密封广泛应用于各种液压装置、建筑机械、矿山机械、航空宇航等设备[5]。
鉴于工程应用中密封工况越来越苛刻,对密封压力提出的要求越来越高,作者对高压往复密封结构进行了研究,本文通过Abaqus对国外某工程机械制造企业使用的高压往复密封结构进行模拟分析,通过对密封结构的密封性能进行研究进而实现结构的优化设计。
1 密封结构仿真模型
VL密封结构图如图1所示。材料参数设定如下:聚四氟乙烯的弹性模量为400MPa,泊松比为0.4;橡胶按照弹性材料进行计算,根据其力学性能,假定其弹性模量为35MPa,泊松比为0.4997;轴的弹性模量为210GPa,泊松比为0.3。橡胶与沟槽的摩擦因数设定为0.3;橡胶与聚四氟乙烯的摩擦因数设定为0.35;聚四氟乙烯与金属的摩擦因数设定为0.04;聚四氟乙烯与聚四氟乙烯的摩擦因数设定为0.04。密封液体压力为21MPa。
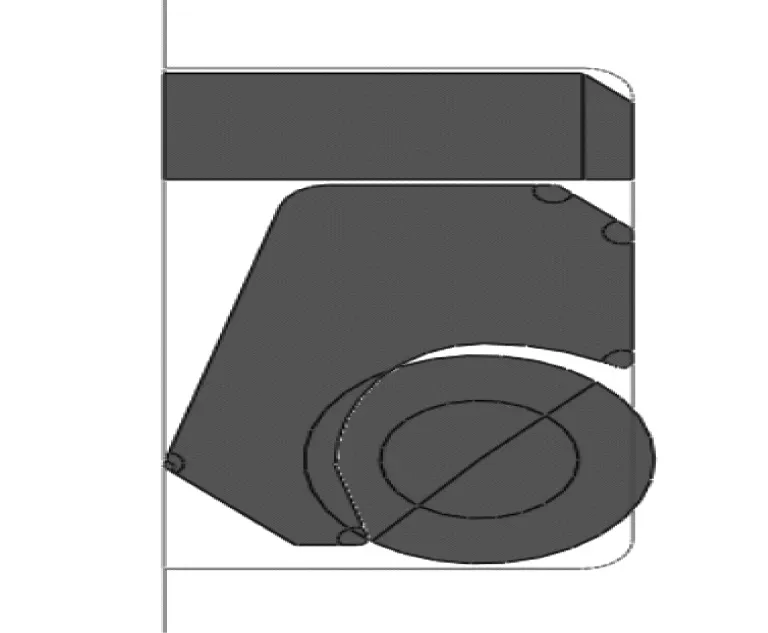
图1 VL密封结构图
2 结果分析
将建立的有限元模型进行计算,得到的应力云图结果如图2所示,聚四氟乙烯的接触应力云图如图3所示,O型圈的接触应力云图如图4所示。

图2 应力结果云图
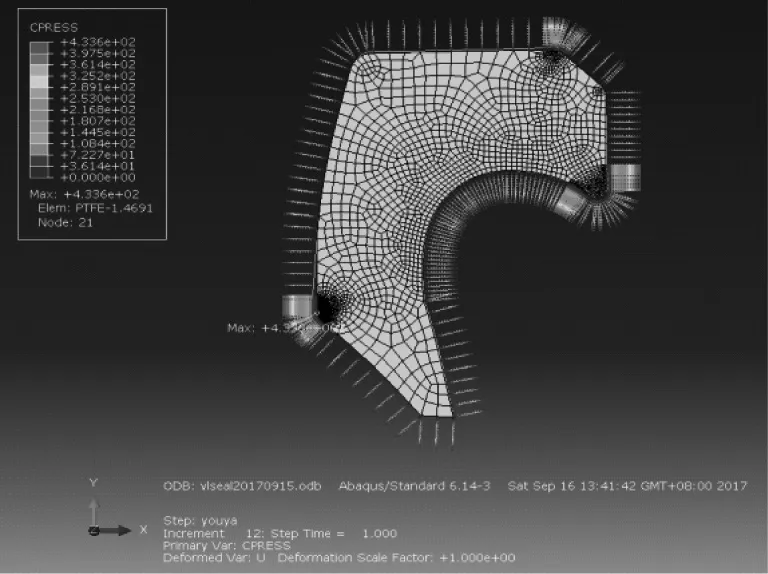
图3 聚四氟乙烯支撑环接触应力云图
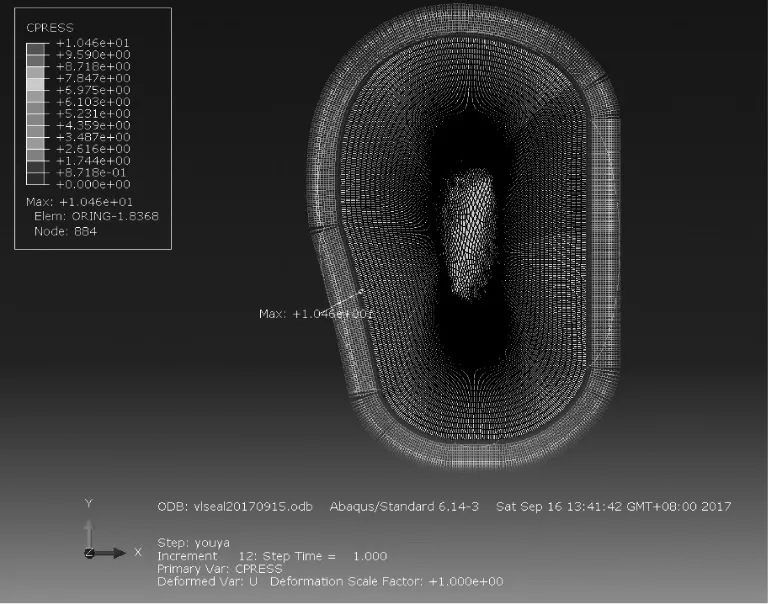
图4 O型圈接触应力云图
从接触应力云图中可以看出,对于21MPa的内压来说,O型圈最大接触应力为10.5MPa,不能形成有效密封,需要通过O型圈的挤压作用,在聚四氟乙烯支撑环与沟槽接触区域形成密封,最大接触应力为28MPa,同时,通过发现可以看到,挡圈的2个接触区域的接触应力均较大,最小的接触应力可以达到46MPa。
2.1 压缩率的影响
橡胶根据其压缩率的大小,其弹性回复力的大小会不同,压缩率越大,橡胶变形越大,其对支撑环的挤压作用越明显,密封性能越强。下面通过改变O型圈的压缩率来观察密封结构的接触应力变化。原计算模型对O型圈的压缩量可以达到0.52mm,其半径为1.76mm,压缩率为14.7%。本文通过增大O型圈直径的方式来降低其压缩率,分别选用直径为3.57mm、3.61mm、3.65mm、3.70mm和3.75mm的O型圈,其压缩率分别为16%、17%、18%、19%和20%。接触应力计算结果如图5所示。

图5 不同压缩率下密封区域的接触应力结果
从结果中可以看出,随着压缩率的增加,接触应力增大,但是随着压缩率增加,接触应力增大的幅值逐渐减小,这与VL密封结构相关,包络线的尺寸影响会在后续计算中进行讨论。两界面间的接触应力与摩擦力成正比,接触应力的增大势必会增加摩擦力,从而造成PTFE与轴间的磨损加剧。对于材料来说,其磨损情况会根据不同磨损工况和垂向应力达到一种平衡,即在特定垂向应力下,其磨损量可以忽略不计,而橡胶材料的压缩率越大,达到这种力的平衡时PTFE的磨损量会越大。
2.2 质心位置的影响
上节计算中可以看到随着支撑环的倾斜,接触应力也会随之变化,而质心的变化也是影响支撑环倾斜的重要因素。从之前的结构设计图中可以看出,支撑环在轴上的支撑点位置与内轮廓的中心点位置水平持平,为了研究质心变化的影响,本文将支撑点的位置进行调节,将支撑环的中心向上调节设定为负,将支撑环的中心向下调节设定为正。本文取-0.5、-0.2、-0.1、0、0.1、0.2 6个结构进行计算对比,将接触应力的计算结果绘制如图6所示。
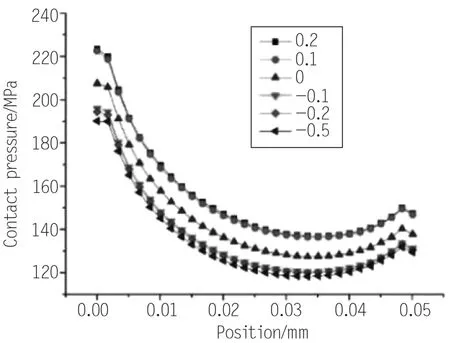
图6 不同质心位置时密封区域的接触应力结果
从计算结果图中可以看出,此图中可以分为质心为正、质心为0和质心为负的3个区域。质心为正和质心为负时接触应力的结果分别集中,-0.1和-0.2的结果相差不大,0.1和0.2的结果相差不大,-0.5的接触应力偏小。随着质心区域的变化,密封结构受压时会发生一定的偏转,按照几何结构推断,结构偏转应该发生一侧接触应力的增大或减小,而此结构中偏转导致整体密封区域接触应力的变化,说明质心偏移时,伴随着PTFE结构支撑部分的厚度变化也对接触应力起到一定的作用:当质心负向偏移时,厚度变薄,整体接触应力变小;当质心正向偏移时,厚度变厚,整体接触应力变大。
2.3 PTFE内侧过盈量的影响
对于组合密封结构来说,密封圈是为了增强密封结构的弹性,而主要的支撑作用是由PTFE来提供的。因此,PTFE的结构尺寸对于接触应力的影响非常大。本节主要依据PTFE与轴的过盈量来对其影响大小进行研究,本节选取过盈量为0、0.1、0.2、0.3 4个数据进行计算,计算结果绘制如图7所示。
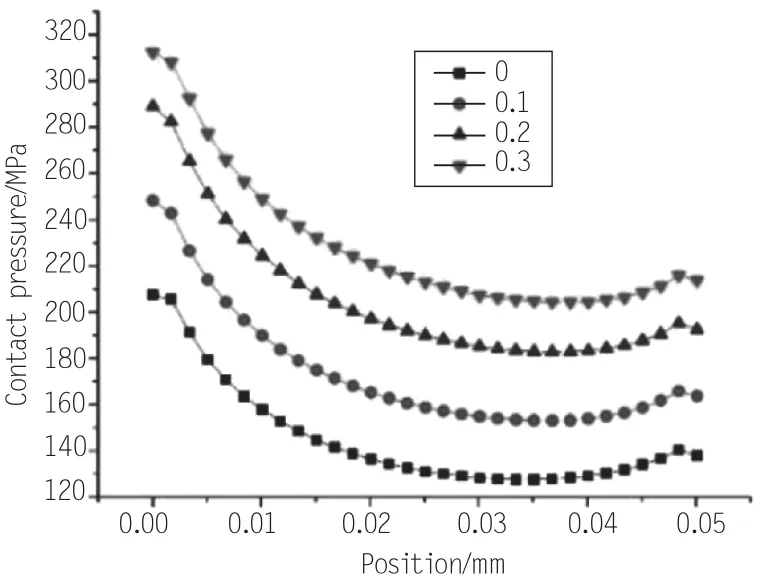
图7 不同过盈量时密封区域的接触应力结果
从结果中可以看出,随着过盈量的增加,接触应力增大,而且随着过盈量增加,接触应力增大的幅值在减小。而且区域左侧的幅值变化较大,这说明,由于过盈量增大,PTFE环发生了一定的偏转。
2.4 PTFE前角角度的影响
本节研究PTFE的前角角度对密封性能的影响,前角角度是指油压侧PTFE环与轴形成的角度。在很多计算中,都会考虑PTFE角度对油压的变化梯度的影响,本节仅考虑此尺寸对接触应力的影响,分别选取前角角度为35°、50°、45°、50°、55°5个角度对此模型进行计算,将计算结果绘制于图8中。
根据计算结果可以看出,随着前角角度的增大,接触应力增大,而接触应力的变化幅值较大处位于左侧(油侧),此点为前角根部,而图中右侧(空气侧)区域变化幅值相对较小,说明前角角度对密封区域右侧(空气侧)影响较小。
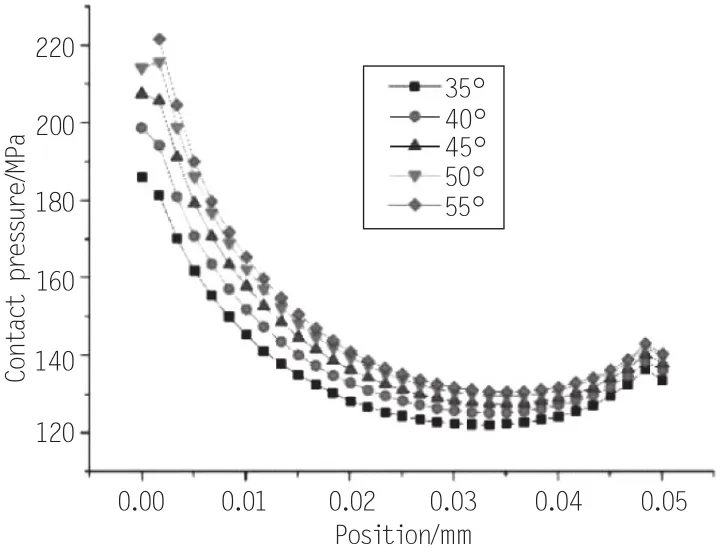
图8 不同前角角度时密封区域的接触应力结果
2.5 PTFE后角角度的影响
本节研究PTFE的后角角度对密封性能的影响,后角角度是指空气侧PTFE环与轴形成的角度。本节仅考虑此尺寸对接触应力的影响,分别选取后角角度为10°、15°、20°、25°4个角度对此模型进行计算,将计算结果绘制于图9中。
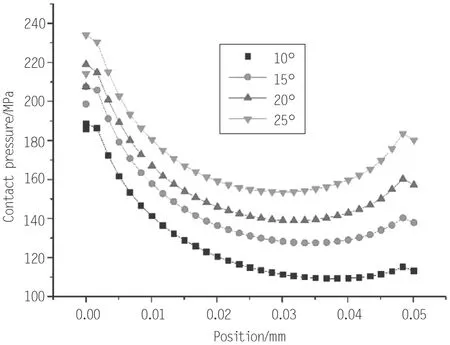
图9 不同后角角度时密封区域的接触应力结果
根据计算结果可以看出,随着后角角度的增大,接触应力增大,而接触应力的变化幅值较大处位于右侧(空气侧),此点为后角根部,而图中左侧(油侧)区域变化幅值相对较小,说明后角角度对密封区域左侧影响较小。
根据对PTFE前、后角的计算可以用于其结构的优化,并根据密封设计压力对前、后角进行优化得到最优的PTFE结构尺寸。
2.6 PTFE包络线优化
对于组合密封来说,O型圈提供了密封所需的回弹力,因此与O型圈所匹配的PTFE包络线对接触应力有一定的影响,在设计时将包络线上部分成左、右两部分,分别由一个椭圆所组成,如图10所示,L1为左侧椭圆的短轴,L2为左侧椭圆的长轴,同时其也是右侧椭圆的短轴,而L3为右侧椭圆的长轴。保持轮廓深度不变,即保持O型圈压缩率不变,然后对这3个参数分别进行参数计算。

图10 包络线示意图
对L1进行参数选择,分别选取其值为1.4、1.5、1.6、1.7mm,将计算的接触应力结果绘制在图11中。根据此图可以判断,当O型圈压缩率不变时,左侧椭圆短轴的尺寸对接触应力影响不大,但同时具备一个趋势,就是L1值越大,接触应力越大。
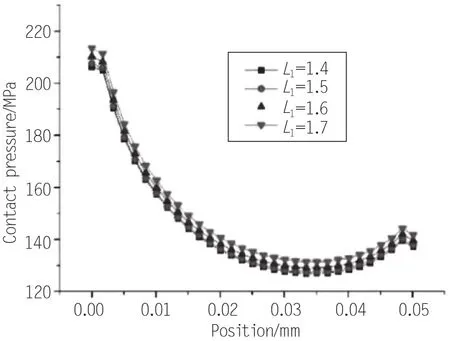
图11 不同L1值时密封区域的接触应力
对L2进行参数选择,分别选取其值为2.065、2.1、2.2、2.3mm,将计算的接触应力结果绘制在图12中。通过结果图可以发现,L2值越大,接触应力越小,我们可以分别将4个参数的O型圈的接触应力云图绘制出来进行对比,其结果如图13所示。
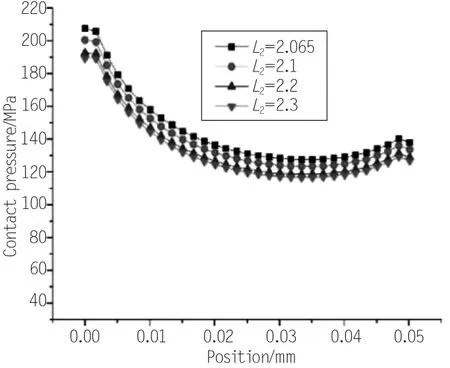
图12 不同L2值时密封区域的接触应力
从图13中可以看到,随着L2值的增加,O型圈的最大接触应力逐渐变小,而其受力位置中右侧上部的接触应力逐渐消失。这说明随着轮廓变大,右侧椭圆的空间区域变大,其对O型圈的挤压作用消失,而使得PTFE密封区域的接触应力下降。
对L3进行参数选择,分别选取其值为2.1、2.27、2.4、2.5mm,将计算的接触应力结果绘制在图14中。通过结果图可以发现,L3值对PTFE密封区域的接触应力影响不大,但是存在一个趋势,即L3值越大,接触应力越小。

图13 不同L2值时O型圈的接触应力

图14 不同L3值时密封区域的接触应力
3 结束语
根据VL往复密封的仿真结果,可以得到以下结论:
(1)此结构的密封性能由PTFE提供,橡胶材料受到压缩后的回复力可以补充PTFE的密封唇的密封效果;
(2)压缩率的大小对密封结构的密封性能影响显著,其对密封结构的磨损的平衡状态也较大。
(3)质心偏移会造成PTFE环有一定的偏转,但是偏转量造成的影响与PTFE环支撑部分厚度上的变化造成的影响相比较小。
(4)内侧过盈量的增加会造成接触应力的增大,但幅值的变化说明PTFE环有一定的偏转,随着过盈量增大,偏转量也在增大。
(5)PTFE前、后角分别对其一侧的接触应力影响较大。
(6)包络线在设计时需要尽量提高O型圈的利用率,使O型圈尽可能多的受到PTFE的挤压,从而提供更多的回复力,增强密封性能。
