自适应模糊滑模控制超声波电动机研究
2018-12-29甘家梁熊曾刚刘桂涛郭海如
甘家梁,熊曾刚,刘桂涛,郭海如
(湖北工程学院,孝感432100)
0 引言
在各种类型电机中,超声波电动机(以下简称USM)具有结构简单,体积小巧,噪声小,无电磁干扰,输出功率密度高,低速时输出力矩大,起停控制时间短,可实现精确定位等特点,因此,在光学精密仪器、机器人、精密机械加工等领域,得到广泛的应用[1]。
由于USM非线性速度特性和速度漂移特性,传统模糊控制算法无法保持长时间精确速度控制。模糊控制算法依赖USM控制经验数据获得控制参数,而USM还未实现高精度控制,没有合适的经验数据[2-6]。为了克服这些问题,许多工程应用专家和学者提出了一系列控制系统方案,但这些控制算法的复杂性远远超出了固定参数PID控制器,需要更高的在线计算能力,从而增加了系统硬件及软件成本。在文献[9-11]中,研究者利用模糊逻辑和神经网络等智能控制策略来处理行波USM控制过程中的非线性问题,需要从控制算法的复杂性和实时控制矛盾之间找到一个折中的控制方案。
本文针对型号规格为GTUSM-60-R-A的行波超声波电动机(以下简称TUSM)研究了一种自适应模糊滑模控制方案。该控制方案是基于模糊逻辑与滑模控制的组合。首先,为了实现没有系统模型情况下的控制规律,设计一个模糊逻辑控制器来预测一个等效控制器,通过自适应法在线估计模糊控制参数。然后,设计一个滑模控制方案,为了保证滑模控制系统的稳定性,防止系统存在的抖动问题,必须对不确定性的边界进行估计。
USM有三种控制方法:驱动电源频率控制、电压幅值控制和两相驱动电压之间相位差控制[6-8]。为了简化驱动电路和控制系统,本文采用驱动电源频率控制。
1 TUSM的数学模型
USM没有磁极与绕组,不依靠电磁介质来传递能量,是通过压电陶瓷元件将电能转换为定子(弹性体)的高频微振动,并通过定子与转子之间的接触摩擦,把超高频微振动转换成转子(移动体)的宏观运动。因此TUSM是一个机电耦合的动力学模型,它涉及到TUSM的定子与转子动力特性,驱动电源的输出动态特性,控制系统的动态特性以及三者结合在一起,构成相互影响、相互耦合的统一的动力学模型[3-7]。
TUSM模型可以用下面的方程来描述:
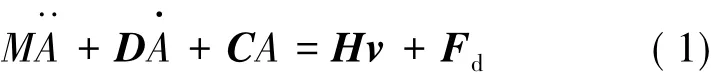
式中:A为USM的振动幅度大小;D是结构的阻尼矩阵,假设为对角矩阵;C是总刚度矩阵;H是机电耦合矩阵;v是电压激励矢量;Fd是定子/转子接触之间相互作用的非线性模态力矢量。
在计算转子的动力学特征时,必须考虑到2个自由度,首先转子的旋转,然后在z方向上运动。z方向的运动由ω表示,垂直转子运动的动力学通过以下方程式表示:

式中:mr是转子的质量;dz是垂直方向上的阻尼系数;cz是等效刚度;Fn是施加的轴向力。因此转子的旋转运动方程由下式计算:

式中:Jr是转动惯量;dr是转子旋转方向的阻尼大小;TL是负载转矩。
本文使用的TUSM为GTUSM-60-R-A,其自带有分辨率为500 ppr的光电编码器。该TUSM的额定输出功率是6.0 W,转速范围是4~150 r/min,额定转速是120 r/min,额定转矩 TN=0.5 N·m,最大扭矩1.6 N·m,使用寿命是1000 h。
为了深入研究控制方案可行性,用MATLABSimulink仿真软件对该电机进行了建模和仿真,测试了其基本运行特性,掌握了驱动电源频率与转矩、速度之间的特性。
图1显示了驱动频率为40 kHz时速度和转矩测量的关系。图2是施加不同负载转矩情况下,电源的驱动频率与速度之间的关系,TUSM的速度在机械谐振频率处具有最大的速度。因此,偏离此频率会降低电机性能。然而,当电源驱动频率降低时,对速度降低的影响会更明显。从图1和图2中的仿真曲线可以验证这个结论。
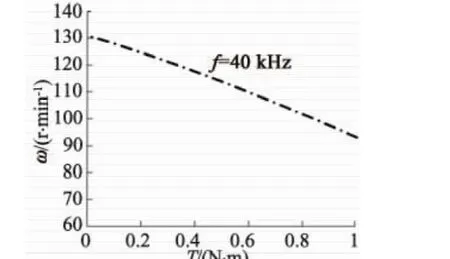
图1 TUSM转矩-速度之间的特性

图2 TUSM电源频率-速度之间的特性
2 自适应模糊滑模控制器的设计
2.1 滑模控制器的设计
为了应用滑动模式控制,把式(3)改写:


图3 TUSM的AFSMC速度框图
考虑到e=ω-ωr作为速度跟踪误差,滑模控制的时变面被定义:

β是一个严格的正常数,后面将阐释如何选择β值。如果滑动面存在,满足以下条件:

因此,控制规律可以由下式获得:
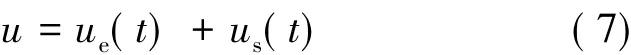
式中:ue(t)是式(6)的解,称为等效控制器。
us(t)称为到达控制律,滑模函数us(t)定义为:

式中:sgn是符号函数。由下式定义:



虽然通过控制律式(7)能够准确地实现滑模控制的动态目标式(5),但在实际应用中,存在切换项K0sgn(s),会使控制系统出现不期望的抖动问题。为了抑制抖动并获得上述精确的控制效率的带宽限制控制器,切换动作函数K0sgn(s)用与滑动面相邻的边界层中的滑模插值代替。因此滑模表示:

sat函数定义:

式中:μ是边界层厚度。
2.2 自适应模糊滑模控制器的设计
根据T-S模糊系统(由日本学者Takagi和Sugeno于1985年首先提出)的通用近似逼近的模糊推理建模法[9-10],存在一个最优模糊控制器,使得模糊控制器的近似误差可以定义:

式中:ε是近似误差,并假设为有界。在这项工作中,模糊规则库中有9条规则,它们具有以下形式:
s和s·是模糊系统的输入变量,u^e是其输出变量。语言变量Ai和Bi被定义:

它们是以对应的隶属度函数为特征。
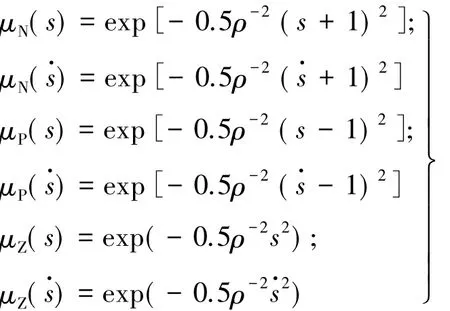
式中:ρ是隶属函数的宽度。
模糊系统的局部控制定义:

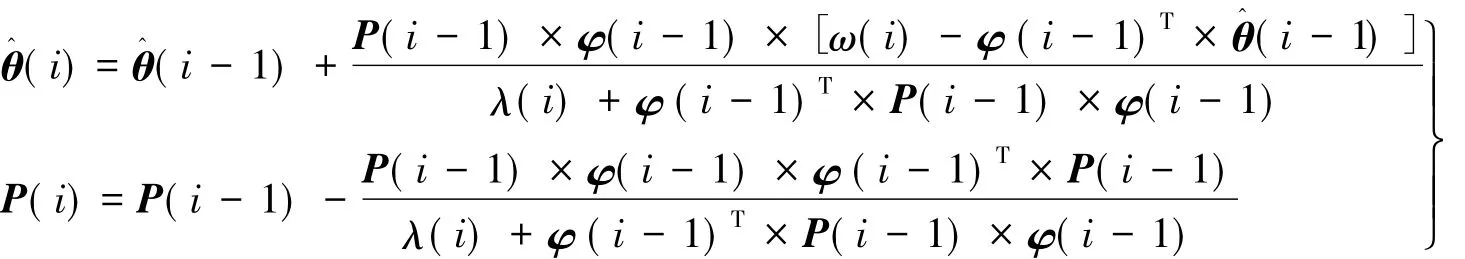
式中:P是协方差矩阵;θ^是θ向量参数的估计,λ表示遗忘因子。通过模糊化,获得模糊输入s和s·通过去模糊化,得到模糊等效控制器:

式中:φ=[s,s·]T。
最后,控制律式(7)通过简化定义:
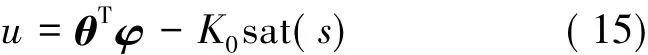
3 仿真结果
为了验证该TUSM的控制方案,对GTUSM-60-R-A进行仿真对比实验。选择s=e·+5e为滑模面,其控制参数如下:K0=0.02,μ=0.01,初始值 θ^(1)=0,p(1)=10 001。未知的扰动由MATLAB函数库中的randn函数建模所得。应用式(15)的控制律,生成模糊隶属函数激励信号如图4所示,USM的速度响应信号如图5所示,图6和图7分别为电机仿真自适应参数θ1和θ2的变化规律。从上述仿真图中分析得出,当施加负载转矩或发生小参数变化时,电动机的转速特性发生变化,但模糊滑模控制器的控制增益也发生变化,以补偿参数变化,动态响应效果是好的。

图4 模糊控制隶属函数u变化规律
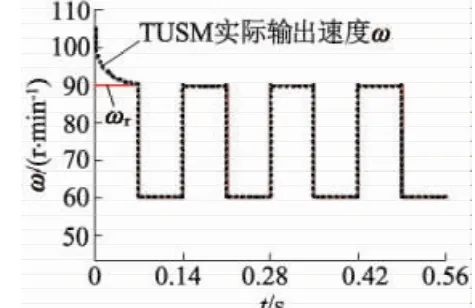
图5 TUSM速度跟踪响应情况
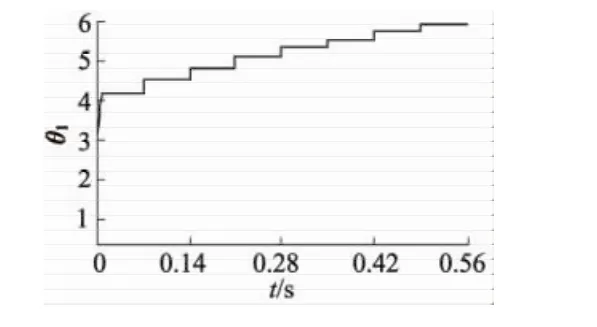
图6 参数θ1随时间的变化规律
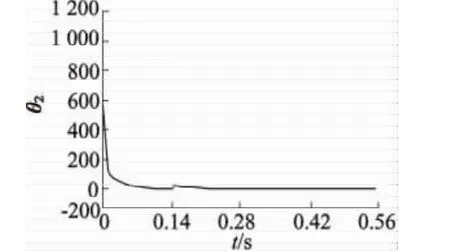
图7 参数θ2随时间的变化规律
仿真实验显示,AFSMC方案,有较好的性能,其控制器变量的变化能在较短的时间内精确地跟踪它们的参考值。
4 结语
本文针对TUSM速度控制,研究了一种自适应模糊滑模控制结构,结合模糊控制和滑模控制的控制策略来保证控制系统的跟踪性能和稳定性。提出的速度控制器的主要优点是对参数变化和外部负载扰动有较好的鲁棒性。仿真结果验证了所提出控制方案的优势。
