基于小波包能量熵的钢轨波磨检测方法

董 伟,黄 文,邢宗义,龙 静

(1.南京理工大学机械工程学院,南京 210094； 2.南京理工大学自动化学院,南京 210094； 3.广州地铁集团有限公司运营总部,广州 510380)

基于小波包能量熵的钢轨波磨检测方法

董 伟1,黄 文1,邢宗义2,龙 静3

(1.南京理工大学机械工程学院,南京 210094； 2.南京理工大学自动化学院,南京 210094； 3.广州地铁集团有限公司运营总部,广州 510380)

针对目前轨道波浪型磨损检测效率慢、成功率低等问题,提出一种基于小波包能量熵的轨道波磨检测技术。首先建立轨道波磨简化模型及车辆集总化参数模型并搭建SIMPACK仿真动力学模型,其次创新性地将小波包和能量熵相结合应用在轨道波磨检测领域,再通过仿真模型得到不同波磨分组下的轴箱振动响应,然后对振动加速度信号进行4层小波包分解并计算各节点的小波包能量和小波包能量熵,最后通过对比分析仿真结果确定轨道波磨故障类型。

钢轨；波浪型磨损；故障诊断；轴箱振动加速度；小波包；能量熵

轨道作为承载列车运行的关键部件，其质量情况影响着乘客乘坐的舒适性以及列车运营的安全性。而在日常的运营过程中，轨道不断接受来自轮对的冲击和压迫，这使得轨道会出现横向和垂向的形变，严重的形变会对列车运营造成巨大的危害。因此对轨道质量状态进行监测，保障轨道安全可靠是地铁公司的检修项目之一[1]。

目前各国均将基于运营车辆的轨道检测技术和装备研制作为研究的重点。Grassie[2]通过对运营车辆轴箱振动以及其他部件振动信号进行分析，并在1996年最早提出基于运营车辆的轨道动态检测构想；HitoshiTsunashima[3]等通过采集车体振动信号并进行小波包分析，发现车体振动信号在某个频域上能够完整表征出轨道波磨故障；曹西宁[4]等通过对采集的轴箱振动信号进行希尔伯特黄变换分析，发现该方法能够对轨道不平顺进行大致的定位；李宏峰[5]等采用SIMPACK软件进行列车仿真建模，对仿真振动信号进行二次积分发现轴箱振动信号能够很好地表征轨道波磨故障；史红梅[6]等研究了基于运营列车振动信号的轨道刚度不平顺和几何不平顺的感知算法，实验结果表明该方法能有效识别和区分轨道故障。

本文提出了基于小波包能量熵的钢轨波磨检测，通过对轴箱振动加速度信号进行小波包能量熵分析，利用SIMPACK对搭建好的模型进行仿真，仿真结果表明小波包能量熵能够很好地确定钢轨波磨故障。

1 模型建立

1.1 轨道波磨简化模型

轨道波浪形磨损是一种周期性的垂向不平顺，因此可以用谐波函数来近似描述轨道波磨。考虑到波磨现象的多样性，若只考虑一种波长的波磨，即可用单谐波函数来描述，如图1(a)所示；若考虑多种波长符合的轨道波磨，则可用多谐波函数描述，如图1(b)所示。

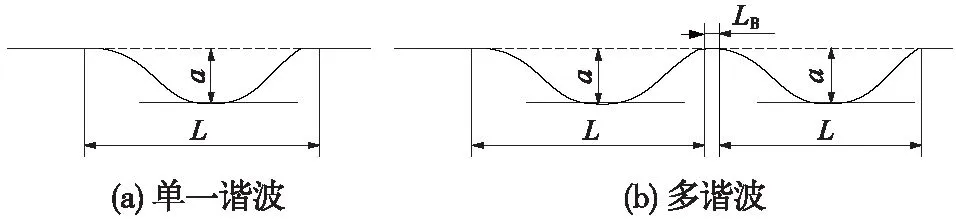
图1 谐波激扰简化模型

对于单谐波函数，其表达式为

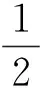
对于多谐波函数，其表达式为

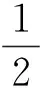
式中，L为波磨波长；a为波磨波深；ω=2πv/L；n为激扰波数。

1.2 列车集总参数简化模型

为了便于分析轨道波磨对轴箱引起的振动变化，需要建立列车集总化参数模型。考虑到簧上部分引起的轴箱振动变化远没有轮轨部分引起的振动冲击明显[7]，因此着重对簧下质量部分进行建模。建立的模型如图2所示。

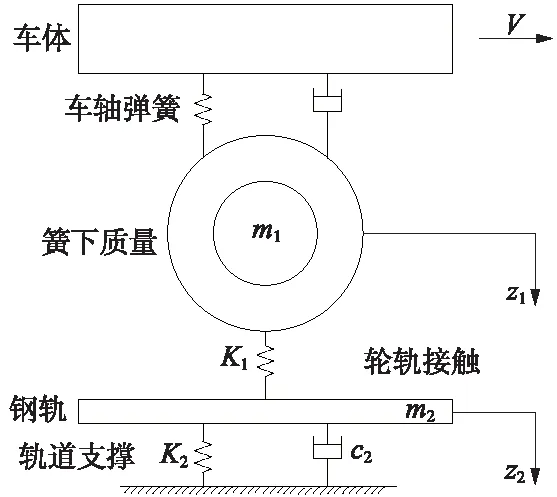
图2 列车集总化模型

图2中，将轮对上部统一称为车体部分，并考虑用有刚度有阻尼的二系簧相连接。轮轨作用部分转化为具有一定质量的轮对通过具有刚度的一系簧和轨道相连接，其中轨道是一个有刚度有阻尼的单自由度系统。图中v为车速，m1为簧下质量，z1为静态下的轮对垂向位移，K1为一系簧的垂向刚度，m2为轨道质量，K2为轨道垂向刚度，c2为轨道阻尼，z2为静态时轨道垂向位移，所有参数向下为正方向。

轮轨的垂向动力学方程在车速v下为

假设轨道波磨为η，则轨道的静平衡位移变为Z2+η，轮轨的垂向动力学方程在车速v下为

将式(4)进行常微分方程求解，可得

以单谐波波形为例，对式(1)进行拉氏变换有

式中，z1(s)和z2(s)为z1、z2的拉氏变换；HZ1(s)和HZ2(s)分别为z1、z2的传递函数。

将式(5)进行拉普拉斯变换，并将式(7)代入计算得

联立以上各式有

HZ1(s)=

式中，Ai，B，C，pi为常数，其大小由ω1、ω2、K1、K2确定。

对式(11)做拉氏反变换得

特别地，当列车以车速v行驶，轨道存在波长为λ的波磨故障，则有波磨的频率为ω=2πv/λ，而轴箱的响应频率为f=v/λ，因此只要知道车速和轴箱响应频率即可求出轨道波磨波长。

1.3 基于SIMPACK的车辆耦合动力学模型建立

SIMPACK软件是由德国航空宇航局于1985年开发，由于其使用了基于相对坐标系递归的优秀算法，使得其相对于其他动力学软件计算方程更少，速度更快[8]。本文使用的是SIMPACK Wheel/Rail模块，即铁路行业专业模块。

SIMPACK建立轨道车辆模型首先要做的就是构建模型拓扑图，拓扑图构建的好坏直接影响建模的好坏、后期计算速度和仿真结果的正确性。SIMPACK中涉及几个建模的重要概念，即：体(Bodies)、约束(Cons-traints)、铰(Joints)、力元(Force Elements)、标记(Makers)等，通常的轨道车辆建模就是先利用以上一些参数进行拓扑图的构建，再创建具体模型。考虑到列车部件的重复性和复杂性，采用自底向上的结构化建模方式，将车体模型按照轮对-转向架-车辆三步进行建模，轨道模型采用刚体模型[9]。其拓扑结构如图3所示。

图3 轨道车辆拓扑图

由图3可看出，将整节车厢分解成车体和子结构两大块，其中子结构中封装了虚车体、转向架构架、轮对。车体和子结构之间采用二系悬挂力元连接；子结构内部转向架构架和轮对之间采用一系悬挂力元连接，并且构架上辅以相应铰接(07号)；轮对和轨道通过09号约束、07号铰接以及89力元相连接。建立拓扑图后，依据轨道车辆参数进行三维实体建模。

SIMPACK建模的过程是参数化的，必须依据实际轨道车辆参数进行相应部件参数设置。选用某型轨道车辆动力学参数建立如图4所示单节车辆模型。

图4 单节车辆模型

2 小波包能量熵

2.1 小波包分析理论

多分辨率分析(Multi-Resolution Analysis)[10]是由S.Mallat于1988年提出的概念，它的核心思想就是不断对信号进行降采样处理从而得到细化的信号特征。关于多分辨率分析可以结合图5用三层结构树进行说明。图中S为原始信号，Ai和Di(i=1，2，3)分别为相应信号段分解后的低频信号和高频信号。由图5可看出一个原始信号在多分辨率分析中只对低频部分做了持续分解，而信号的高频部分在第一层分解后就不再进行任何处理。一个信号经过三层多分辨率分析后的关系可表示为：S=A3+D3+D2+D1。

图5 三层多分辨率分析结构树

虽然多分辨率分析的出现是时频信号处理的一次革命，但由于它自身算法对高频信号处理的忽视性，使得它先天就存在对高频信号处理能力的不足。因此针对这一缺陷，M.V.Wickerhauser和R.Rcoifman在小波分析和多分辨率分析的基础上提出了小波包分析。

小波包分析[11](Wavelet Packet Analysis)在原有多尺度分析的基础上进一步优化，将多分辨率分析中忽略的高频信号也做同低频信号一样的逐层细化分解，即小波包分解能够对信号低频和高频部分同时进行多尺度分析，提供多尺度分解[12,13]。原始信号经过三层小波包分解后的结构树[14]如图6所示。

图6 三层小波包分解结构树

2.2 小波包能量熵理论

在信息论中，熵被用来衡量一个随机变量出现的期望值[15]。信息熵理论是香农于1948年提出，他认为一个信号的信息熵越大，则它出现的各种可能性就越高[16]。根据信息熵理论：假设有一随机变量X={x1，x2，x3…xn}组成的信号，信息熵的计算公式如下

式中，H(X)为信息熵测度;pi为取值概率。

由于信息熵能够反映信号出现随机变化的程度，对于某个信号源，其信息熵越大即表示该信号在采样范围内的幅值波动越大，相反信息熵越小该信号越趋于平稳。因此一段信号的平均统计特征大小通常可以用这段信号的信息熵大小来表示。因此其在故障诊断领域有着重要的作用。

假设有一待分析信号，其信号长度为N，该段信号的小波包能量熵可由以下步骤求得。

(1)对待测信号进行j层小波包分解，经过分解后得到一系列不同频段的子信号序列。

(2)将得到的高低频序列的小波包重构系数表示为Sjk，(k=0，1，…2j-1)。

(3)计算每个子序列的小波包能量值Ejk，(k=0，1，…2j-1)。

式中，Ai(t)为该节点处的幅值最大值;ti-1和ti分别是该节点信号的起止时间。

(4)求取总能量值E

(5)计算每个子节点能量相对于总能量的概率pjk

(6)求取小波包能量熵值测度

式中，Hjk为信号j层分解后的第k个小波包能量熵测度。

3 仿真设计

3.1 算法流程

基于小波包能量熵的轨道波磨故障检测算法流程如图7所示，其主要步骤为：

(1)对采集的轴箱垂向振动信号进行滤波处理，滤除噪声和其他干扰项，只保留和轨道波磨相关的振动信息；

(2)对滤波后的轴箱垂向振动信号进行j层小波包分解，使信号分解成2j个包含不同频率带的子节点信号；

(3)计算分解后信号的小波包能量，这其中包括各节点的小波包能量以及信号总的能量值；

(4)依据式(16)和式(17)计算各节点的小波包能量熵Hjk；

(5)计算分解信号的总熵H并和阈值进行比较，若总熵超出阈值，则判定该段轴箱振动信号包含轨道波磨故障，相反则不存在轨道波磨故障；

(6)若信号存在轨道波磨故障，对小波包分解信号进行频率分析，找出时域上的频率高集中区域，计算出轨道波磨在轨道上的具体故障位置以及根据频率集中带计算出波磨故障的波长范围。

图7 小波包能量熵检测轨道波磨算法流程

在实际工程应用中，由于背景噪声的存在，必须对轴箱振动信号进行滤波处理，基于SIMPACK软件仿真出的轴箱振动信号并没有受到噪声信号干扰，所以算法流程中的滤波处理可以暂不考虑。

3.2 数据准备

国内外铁路行业习惯使用功率谱密度函数(power spectral density)来表示正常轨道的不平顺程度变化[17]。它是以频率为横坐标，PSD为纵坐标来表示的一条曲线。目前我国学者普遍认为美国五级轨道谱较为符合我国现有轨道情况。本文采用在轨道谱上叠加波磨数据的方法进行轨道波磨设置。

为了更为全面地验证检测算法的可行性，选取14组波长不同的波磨叠加五级轨道谱垂向信号进行仿真实验。SIMPACK仿真实验时，设定轨道长度为95 m，采样频率为1 kHz，在0～50 m处左右轨均为不做任何处理的轨道，50～95 m处右侧轨道分别设定14组不同的波磨故障信号，左侧轨道只添加美国五级轨道谱垂向不平顺，具体设置参数如表1所示。

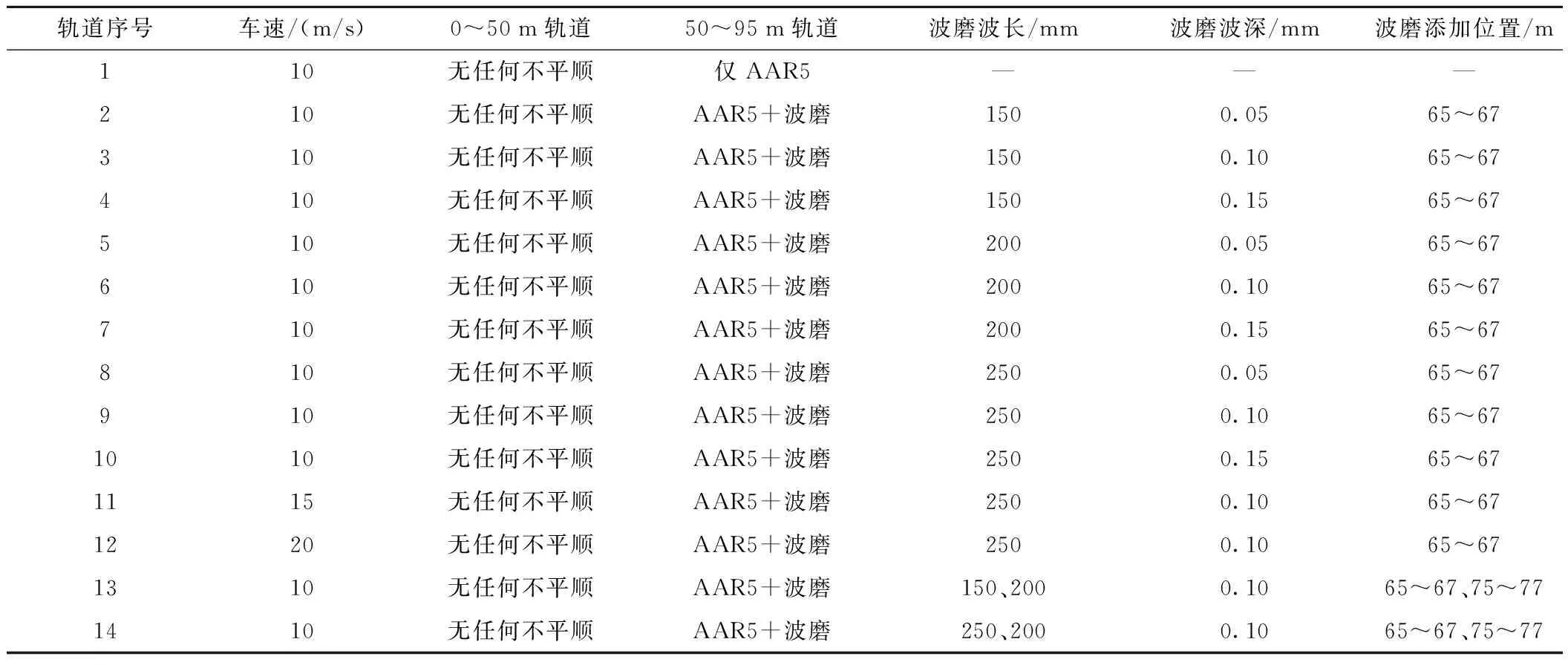
表1 轨道波磨分组设置参数

3.3 仿真结果

通过对上面分组线路得到的仿真轴箱振动信号进行数据分析，从两个方向进行轨道波磨故障诊断。首先是对轴箱振动信号进行小波包能量熵计算，通过阈值判断轨道是否存在波磨故障，然后对故障轨道进行小波包时频图分析，定位轨道波磨故障时域位置及确定波磨波长范围。

(1)轨道波磨检测阈值的设定与故障判断

根据图7轴箱振动信号进行小波包分解，选用db4小波作为小波母函数，分解层数暂定为4层，计算得到各节点的小波包能量熵后，根据式(17)计算4层小波包分解后的总熵值，计算结果见表2。

表2 各分组实验总熵计算结果

对表2进行分析可看出，第一组轨道仅包含美国五级轨道谱，其小波包能量熵为1.835 6×10-5，而其余13组包含波磨的轨道小波包能量熵值范围在0.3～2.5，由此可看出,包含轨道波磨段的轨道其小波包能量熵远大于无故障轨道；进一步分析波磨波长相同但波深不同的轨道，例如当波长为150 mm，波深分别为0.05、0.1、0.15 mm时，小波包能量分别为1.996 4、2.310 5和2.345 0，小波包能量熵基本和波深呈正相关关系，其余波长下也有相同情况；交叉分析不同波长，相同波深情况下的小波包能量熵，例如当波长分别为150、200、250 mm，波深为0.10 mm时，小波包能量熵值分别为：2.310 5、1.833 4和1.497 7，可发现在波深相同情况下波长越小，小波包能量熵越大，且其余波深下也会有类似情况；对比第9组、第11组和第12组数据，相同波磨故障状况，不同列车运行速度，在速度分别为10、15，20 m/s情况下，小波包能量熵分别为1.497 7、1.773 6和1.794 8，可看出小波包能量熵随着速度的增加而增加。对比第13组和第14组实验，当有两组不同波长波磨分别叠加轨道不同位置时，叠加波磨波长越大，小波包能量越小。

综合以上分析结果可以得出,小波包能量熵在轨道波磨故障检测上有着明显的度量性，其值的大小受波磨故障的波长、波深以及行车速度影响，且与这三者均有着明显的线性关系，因此可以将轴箱振动信号的小波包能量熵值作为轨道波磨故障检测的阈值参考。在本次仿真中综合以上数据结果，建议将阈值设定为0.3，若计算得小波包能量熵值大于0.3,则判断发生波磨故障，反之则无波磨故障。由于阈值的选取与车辆运行状态、车辆速度等相关，因此需要通过后期根据现场实际情况进行标定调整。

(2)轨道波磨故障波长的检测

通过对信号的小波包能量熵计算可以判断轨道波磨故障是否存在，本节通过对信号进一步分析来确定故障段的时域位置及波磨波长。

选取表1中的第3组、第6组和第9组数据进行分析。对分解后的子节点信号进行小波包时频分析，3组数据的二维时频图如图8～图10所示。

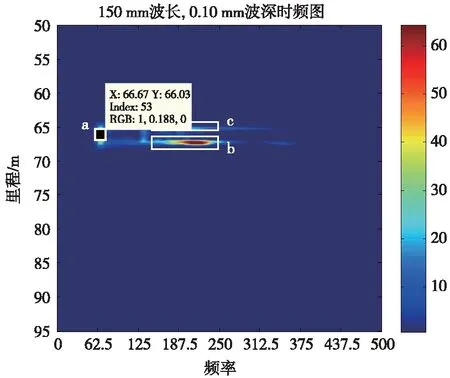
图8 第3组实验时频图分析

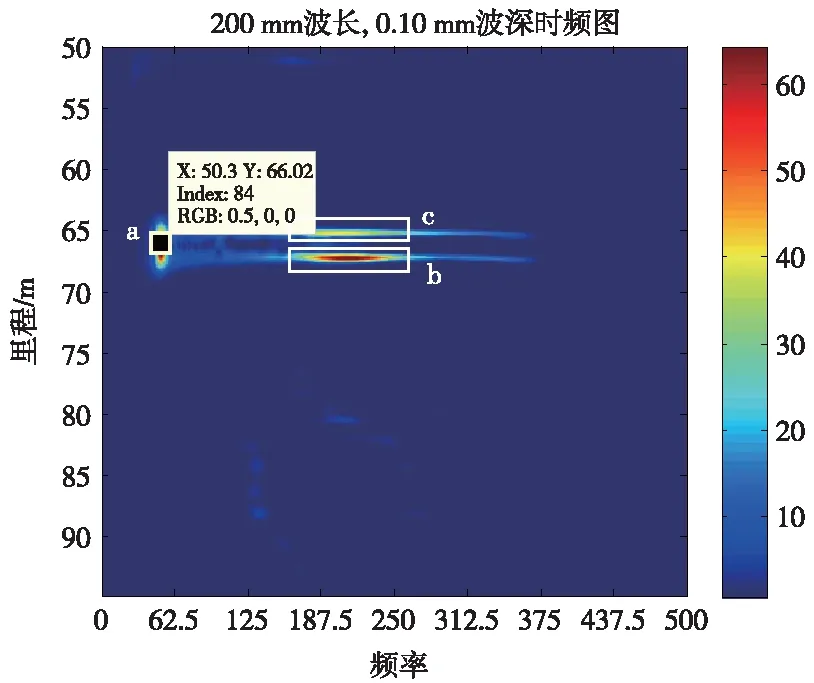
图9 第6组实验时频图分析

图10 第9组实验时频图分析

图11 第13组实验时频图分析

根据小波包分解可知4层小波包分解的16个节点分别对应一个频率范围，由于采样频率为1 kHz，因此每个频带的范围为500/16=31.25 Hz。根据第一节中的推导可知，波磨长度和轴箱振动频率有如下关系

式中，λ为波磨波长;ω为振动频率，v为行驶车速。

由图8～图10分别得出波磨故障引起的振动中心频率为：66.67、50.3、39.91 Hz，得出对应波磨波长为149.99、198.81、250.56 mm。观察图11，a处故障中心频率为65.22 Hz，b处故障中心频率为49.78 Hz，计算对应波磨波长分别为153.32、200.88 mm。可见诊断结果和实际波磨设置参数基本吻合，最大误差为2.21%。

观察图8～图10可看出，3幅图中均存在不止一处的高频率集中区域，如图8～图10中方框a、b、c所示。而在仿真中只设定了1处波磨故障，b、c两处的高频率集中区域呈现很明显的横向集中性，即频率跨度很大而里程跨度很小，并且两个高频率集中区域分别是在设定波磨段的首尾段。因此可以认为这两处的频率集中区域是由于车辆经过波磨和非波磨段过度区域时引起的冲击变化，而真正的波磨段引起的时频图变化区域应该是a区域所示。

4 结论

本文基于小波包分解和信息熵理论研究了一种基于小波包能量熵的钢轨波磨故障检测方法。首先建立了轨道波磨简化模型和列车集总参数简化模型，验证了基于轴箱振动信号检测轨道波磨的可行性。然后利用SIMPACK多体动力学软件对模型进行仿真。并创新性地将小波包能量熵运用于轨道波磨检测上；随后通过设定14组不同类型的轨道波磨故障形式进行仿真实验。仿真实验结果表明，小波包能量熵能够很好地判断钢轨波磨故障的情况。

[1] 高雨峰，王福田，刘仍奎.铁路轨道状态分析信息系统设计与实现[J].中国安全科学学报，2006，16(7):128-132.

[2] Grassie S L. Measurement of railhead longitudinal profiles: a comparison of different techniques[J]. Wear， 1996， 191(1):245-251.

[3] Tsunashima H， Mori H， Yanagisawa K， et al. Condition monitoring of railway tracks using compact size on-board monitoring device[C]∥Railway Condition Monitoring (RCM 2014)， 6th IET Conference on. IET，2014:1-5.

[4] 曹西宁，柴晓冬，郑树彬.基于Hilbert-Huang变换的轨道车辆轴箱加速度信号分析[J].仪表技术与传感器，2015(3):92-95.

[5] 李宏锋.地铁轨道波浪形磨耗检测系统研究[D].成都：西南交通大学，2014.

[6] 史红梅.基于车辆动态响应的轨道不平顺智能感知算法研究[D].北京：北京交通大学，2013.

[7] 张健，金学松，肖新标，等.车辆-轨道耦合动力学钢轨模型求解方法[J].交通运输工程学报，2011，11(2):32-38.

[8] 缪炳荣，方向华，傅秀通.动力学分析基础教程[M].成都:西南交通大学出版社，2008.

[9] Kurzeck B. Combined friction induced oscillations of wheelset and track during the curving of metros and their influence on corrugation[J]. Wear， 2011，271(1):299-310.

[10] 刘珊，曹海泉，于海，洪刚.基于小波包能量熵的变压器振动信号特征研究[J].电网与清洁能源，2010(5):35-38.

[11] 杨江天，赵明元，张志强，李平康.基于定子电流小波包分析的牵引电机轴承故障诊断[J].铁道学报，2013(2):32-36.

[12] 肖玉飞，刘祖润，李目.基于小波包能量熵与SVM的模拟电路故障诊断[J].电子测量技术，2011(6):110-113.

[13] 武兵，曹勇敢.基于小波包能量熵的输电线路两相接地故障甄别[J].河南电力，2016(1):15-19.

[14] 赵志宏，杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断[J].振动.测试与诊断，2012(4):640-644，692.

[15] 安春兰，甘方成，罗微，秦发园.提速道岔小波包能量熵故障诊断方法[J].铁道科学与工程学报，2015(2):269-274.

[16] 李彦苍，彭扬.基于信息熵的改进人工蜂群算法[J].控制与决策，2015(6):1121-1125.

[17] 赵永超.无砟轨道结构振动响应的概率分析[D].长沙：中南大学，2009.

A Rail Corrugation Detection Method Based on Wavelet Packet-energy entropy

DONG Wei1, HUANG Wen1, XING Zong-yi2, LONG Jing3

(1. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China; 3. Guangzhou City Underground Railway Corporation, Guangzhou 510380, China)

Aiming at the problem of low efficiency and low success rate in rail corrugation detection, a method based on wavelet packet-energy entropy is proposed. Firstly, physical fitting models of rail corrugation and the train are established and a coupling dynamics model is set up based on SIMAPCK. Then wavelet packet-energy entropy is introduced creatively in the area of rail corrugation detection. Furthermore, four-layer wavelet packet decomposition of the axle box vibration acceleration signal is performed, and wavelet pocket-energy entropy and wavelet energy of each nod are calculated. Finally the simulation results are compared and analyzed to determine the type of rail corrugation.

Rail; Corrugation; Fault diagnosis; Axis box vibration acceleration; Wavelet packet; Energy entropy

1004-2954(2018)01-0052-07

2017-02-27；

2017-04-07

国家重点研发计划项目(2016YFB1200402)；国家工程实验室建设项目(2016582)

董 伟(1992—)，男，硕士研究生，主要从事运输信息工程与安全保障研究，E-mail：njustdongwei@163.com。

U213.4+2

A

10.13238/j.issn.1004-2954.201702270001