基于模型驱动的田间数据压缩采集方法研究

饶 元，许文俊，赵 刚，Arthur GENIS，李绍稳

(1.安徽农业大学 信息与计算机学院，安徽 合肥 230036；2.Katif沿海沙漠开发研究中心，以色列 内提沃特 8771002)

农业物联网系统已经成为农业大数据最重要的数据源之一。通过部署于田间地头的传感器节点，农情数据可被实时感知，并发至数据中心，这使得现代农业生产实时远程监控和精准管理成为可能[1-2]。物联网农情监测网络通常部署在野外环境，持续供电困难。监测节点以无人值守的方式可靠运行，并实现数据的持续高质量采集是农业无线传感器网络部署应用需要解决的核心问题之一。然而，大量冗余数据的无线传输不可避免地会引起传输冲突和能量浪费[3]。数据压缩传输技术能够有效降低网络数据传输量，减少节点的数据通信量和能耗，是解决上述问题的有效手段[4-6]。

鉴于节点感知数据通常都具有较高的时间相关性，基于模型驱动的数据压缩采集方法引起了广泛研究兴趣[7-9]。文献[10-11]利用差分自回归移动平均模型(ARIMA)预测室内光照和温度，抑制了数据传输量，提高了能量利用效率，但存在低阶模型预测精度低、高阶模型参数确定难度大的不足。相关研究利用线性模型具有较低计算开销的特征，提出基于线性回归的无线传感器网络分布式数据采集优化策略[12-13]，如利用线性模型(DBP)实现公路隧道内的光照数据压缩采集[14-15]，和基于分段线性回归的多参数无线传感网数据融合算法[16]，均能降低网络的总能量消耗，延长网络的生命周期。机器学习预测方法具有对数据非线性和不确定性变化规律进行精确描述的能力。支持向量回归模型(SVR)被广泛用于构建病虫害、旱情等预测预报模型[17]。时钟驱动循环神经网络(CW-RNN)被用于河流的流量预测等[18]，但存在收敛速度慢、训练数据大等缺陷。

以上研究鲜有涉及模型训练参数设置、模型适应性综合评价与实际应用甄选标准。自动观测数据的质量控制是开展农业生产分析以及基础科研数据应用的重要前提[1]。鉴于此，本文依托实验区域田间数据，探索ARIMA、SVR、DBP和CW-RNN等数据预测模型的关键训练参数设置，开展模型适用性评价，以期为丰富模型驱动的田间数据收集的理论与实践提供参考，为实现农情数据的高质量、低代价采集提供指导。

1 材料与方法

1.1 数据来源

实验数据来自安徽农业大学农萃园，自2016年3月13日起部署传感器节点不间断监测园区作物育苗温室大棚内外的环境信息、花卉植株的茎秆微变化等本体信息，采样间隔为10 min。本文取2017年5月3—10日共8 d(192 h，1 152数据点)时间段内空气温度、风速、果实膨大和土壤湿度观测数据(图1)。其中，空气温度和风速等呈现明显周期性特征，土壤湿度和果实膨大呈线性变化。具体地，4种数据特征分别为周期性、带振荡值的周期性、线性和带振荡值的线性。以前7 d数据作为训练集，第8天数据作为测试集。

1.2 模型驱动的数据收集框架

如图2所示，模型驱动的数据收集框架中，网关/服务器、传感器节点进行双端预测来降低数据传输量。具体流程：网关/服务器基于前期采集到的数据进行模型训练，然后将模型/参数传输至执行数据收集的传感器节点。传感器节点端定期获取、同步评估预测值与实际收集值的误差。若误差超过阈值，传感器节点将向网关/服务器上传所采集的数据，由网关/服务器重新训练模型后，再将模型/参数同步至传感器节点。若误差在阈值以内，则传感器节点不上报数据，服务器端将在其他时刻自动触发模型预测填充该部分数据，从而大幅度减少传感器节点的数据传输量。

1.3 适用性评价标准

逼近最优排序法(TOPSIS)是一种基于多目标的评价法，根据有限个评价模型与理想化指标组合的接近程度进行排序，测量目标模型靠近最优指标向量和远离最劣指标向量的程度，以此评估模型的性能水平[19]。本文运用熵权TOPSIS评价预测模型适用性，具体如下。

1)数据规范化。采用向量规范法对预测模型的评价指标数据进行规范化处理，向量规范化后各模型的同一指标平方和为1，计算方法如下：

(1)

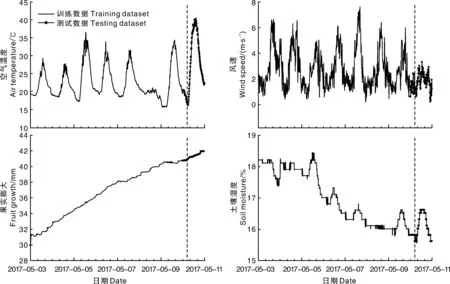
图1 育苗温室内外的监测数据Fig.1 Monitoring data inside and outside nursery greenhouse

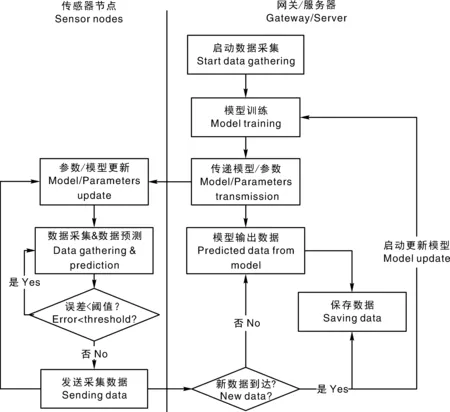
图2 模型驱动的数据收集框架Fig.2 Framework of model-driven data gathering

式(1)中：Xij表示指标i在第j个预测模型的初始评价值，n为参与比较的预测模型总个数，l为指标个数，Sij为Xij的规范化矩阵。

2)熵权法。熵权法通过评价预测模型的各项指标值来确定指标权重，增强指标的分辨性和差异性，具有操作性和客观性强的特点。评价模型在某项指标上的值相差越大，则相应权重越大。根据各项指标的差值程度，客观计算各项指标权重，为多指标综合评价提供依据。计算方法如下：

(2)

3)构建规范化加权矩阵。熵权法所确定的权重向量wi与规范化矩阵Sij=(sij)n×l进行向量积运算，得到加权规范化矩阵：

(3)

4)定义预测模型的最优、最劣指标向量。令V+、V-分别表示最优指标向量和最劣指标向量，则有：

(4)

式(4)中vij为模型i中第j项指标的规范化加权值。

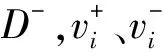
(5)

6)计算评价目标与最优指标组合方案的贴近度Ci。

(6)

式(6)中Ci值越大，表明预测模型j的性能越接近最优水平，反之对象性能差，甚至无法达到使用水平。

1.4 数据预测模型

本文拟评价的预测模型有ARIMA、SVR、DBP、CW-RNN和常量模型Constant。先从数学和统计学角度简述各预测模型的运行机制。

1.4.1 ARIMA

ARIMA是一种常用的时间序列预测模型，系一种有效的动态数据处理参数化时域分析方法。建立ARIMA模型要求时间序列是平稳随机过程，因此在建模之前必须检验时间序列数据的平稳性。若数据序列具有非平稳性特点，则须对其进行差分处理，使之成为平稳时间序列。设有时间序列X={x1，x2，…，xt}，则 ARIMA模型预测方程[10-11]可表示为

(7)

1.4.2 SVR

SVR模型通过非线性映射函数Ф将数据xi映射到高维特征空间，再进行线性回归。对于给定样本数据集{(xi，yi)，i=1，2，...，k}，SVR具有如下形式[17]：

y=wФ(x)+b，

(8)

式(8)中：w为权值向量，b为偏置量。

为提高模型的泛化能力，既要考虑经验风险的最小化，也要降低模型复杂度，故常利用带松弛因子的拉格朗日函数解出最优参数。在时间序列预测中，高斯核函数通常具有较好的效果[17]。

1.4.3 DBP

给定样本数据集{(xi，yi)，i=1，2，…，k}，DBP基于短中期内的数据大多可近似为线性的思想，从前期收集的m个数据点中前后各截取u个数据点，以前后h个数据点的平均值建立线性模型[14-15]：

y=αx+β。

(9)

通过设置误差阈值ε、异常时间阈值εT调控预测精度和模型更新。若预测误差连续偏离误差阈值ε的次数超过εT时，传感器节点将开始向Sink端发送数据，随后Sink端启动模型更新。由于模型是线性的，网关/服务器、传感器节点两端进行模型更新时仅需传输斜率α和截距β。

1.4.4 CW-RNN

CW-RNN结构与标准人工神经网络类似。它将隐含层节点分成若干模块，各模块均分配独立时钟周期Ti，独立学习某特定波长，横向联结模块学习长短波间的相互影响。运算时进行分块管理，选择部分模块参与运算，不参与运算的模块置0。CW-RNN中隐含层的各模块内部节点是全连接，模块之间均从高时钟频率模块指向低时钟频率模块。

通常，Ti=2i-1。经典CW-RNN的前反馈计算公式[18]为

ht=σ(Wx*Xt+Wh*ht-1)，

(10)

式(10)中：t时刻的隐藏状态ht由输入训练样本Xt和ht-1共同得到；σ为CW-RNN激活函数，序列预测时多采用tanh，分类模型时通常选择Softmax；Wx和Wh2个矩阵是CW-RNN模型的线性关系参数。CW-RNN通过强制性地把Wh参数矩阵设置成上三角阵，控制模块之间连接的方向。

1.4.5 常量模型Constant

Constant将当前收集数据作为下一时刻的预测值，其本质是通过直线y=yi近似表示一段时间内数据的变化情况。对于给定的最新收集数据yi，则下一时刻收集数据预测值为yi+1=yi。因此，若满足误差阈值ε，未来一段时间的数据预测都等于yi。Constant模型不需要训练数据，预测值超出误差阈值时，传感器节点将最新数据上传至网关/服务器端，不会传递模型/参数。该模型运行代价低，易于在资源有限的传感器节点上实现[8]。

2 结果与分析

采用参数平均绝对百分数误差(MAPE)评估预测模型的精度。MAPE是相对值，很适合于相同目标数据不同预测模型的预测精度评估，值越小表示预测精度越高。其计算公式如下[8]：

(11)

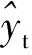
为直观展现数据压缩采集性能，采用数据传输率TR评估模型的数据压缩传输效果，计算公式如下：

(12)

式(12)中：Tran表示实际传输数据量，Amount为总待传数据量。

2.1 模型训练参数设置方法

为探索训练长度等参数的设置，系统分析ARIMA、SVR、DBP、CW-RNN和Constant等5种模型在用于预测4类数据场景时，训练长度与预测长度间的耦合关系。训练长度指训练模型过程中所使用的数据点的数量。预测长度是模型不设置误差阈值时，一次预测输出的数据点总数。取多个不同预测起点预测误差的平均值作为最终评价MAPE。结合算法运行机制，针对ARIMA模型，将1 008个(7 d)训练数据分为9(1/16 d)、18(1/8 d)、36(1/4 d)、72(1/2 d)、144(1 d)、288(2 d)、504(3.5 d)和1 008(7 d)。SVR和DBP算法的训练数据均分为2、3、4、5、10、15、20、25个数据点。由于CW-RNN需要保持时钟记忆长度，训练长度需要大于36(1/4 d)，故在ARIMA训练数据划分基础上剔除长度9和18，增加训练长度432(3 d)和720(5 d)。Constant只需1个最近历史数据即可。

如图3所示，各模型的预测误差MAPE均随着预测长度的增加而上升，尤其当预测长度大于36后MAPE显著上升。在某些预测起点，模型的长期预测甚至难以跟踪实际数据的动态轨迹，表明模型长期预测存在较大的困难。不同于预测长度，预测模型(Constant除外)的最佳训练长度取决于其自身特征和所预测的数据对象。具体地，仔细分析5种模型在(振荡)线性、(振荡)周期性数据下不同预测起始点的预测效果，可得出：ARIMA采用较短的训练长度(9个数据点)或1 d的长度(144个数据点)均能够取得较好的效果。SVR对训练长度不敏感，过长的训练长度(大于10个数据点)反而导致性能下降。DBP的训练长度为6，边界数据点个数为2，异常数据点个数阈值εT为2时效果最佳。对振荡型数据(风速、土壤温度)，5种模型的MAPE明显高于其他数据类型。CW-RNN模型至少需要72个训练数据点，且预测效果劣于其他模型。Constant模型的误差与其他模型较为接近，因无须训练，不存在训练长度。

2.2 误差阈值设置方法

误差阈值是决定业务数据传输率、保证数据采集质量的关键因素之一。本文采用前期采样数据值来定义误差阈值，形式如下：

η=(Smax-Smin)*To，

(13)

式(13)中：Smax、Smin分别为前期(半天)采集数据的最大、最小值。To为误差容忍度，其值越大则误差阈值越高，采集到的数据精度越低。图4表示的是To与数据采集误差MAPE、业务数据传输率间的耦合关系。随着To的变化，MAPE与业务数据传输率间呈相反的变化趋势。选择使业务数据传输率和MAPE达到平衡的点所对应的To值作为误差容忍度最优值。

具体的平衡点因预测模型和数据类型的不同而有所差异。以空气温度数据为例，CW-RNN模型的平衡点约为2%，DBP模型的平衡点约为5%，其他模型的平衡点介于两者之间，故收集空气温度数据时To的最优取值区间为[2%，5%]。同理可得，风速、果实膨大和土壤湿度的To取值区间分别为[4%，15%]、[4%，10%]和[4%，8%]。

2.3 模型适用性评估

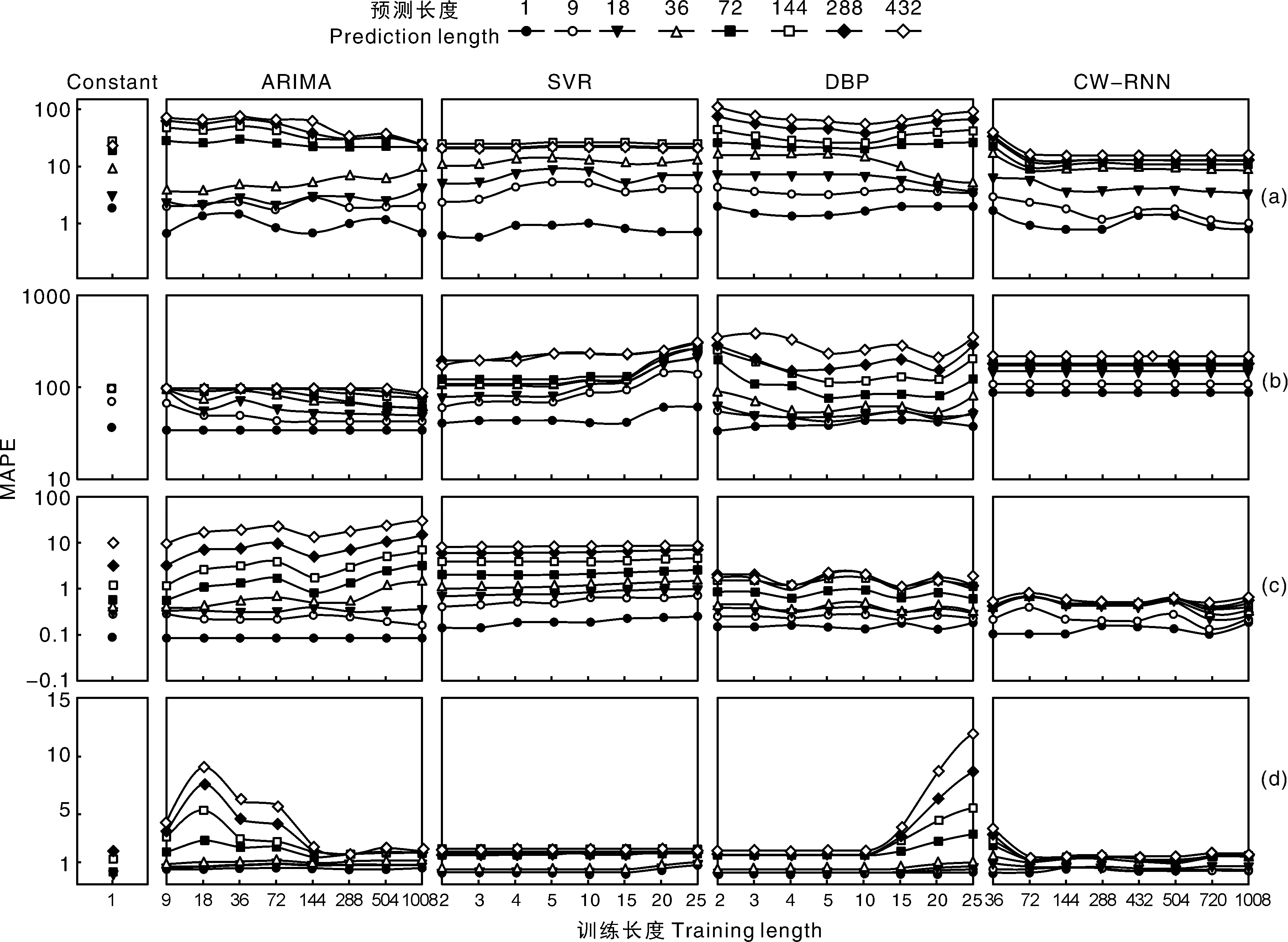
a, 空气温度; b, 风速；c, 果实膨大；d, 土壤温度。a, Air temperature; b, Wind speed; C, Fruit growth; d, Soil moisture.图3 模型训练长度与预测长度耦合关系Fig.3 Coupled relationship among model training and prediction lengths

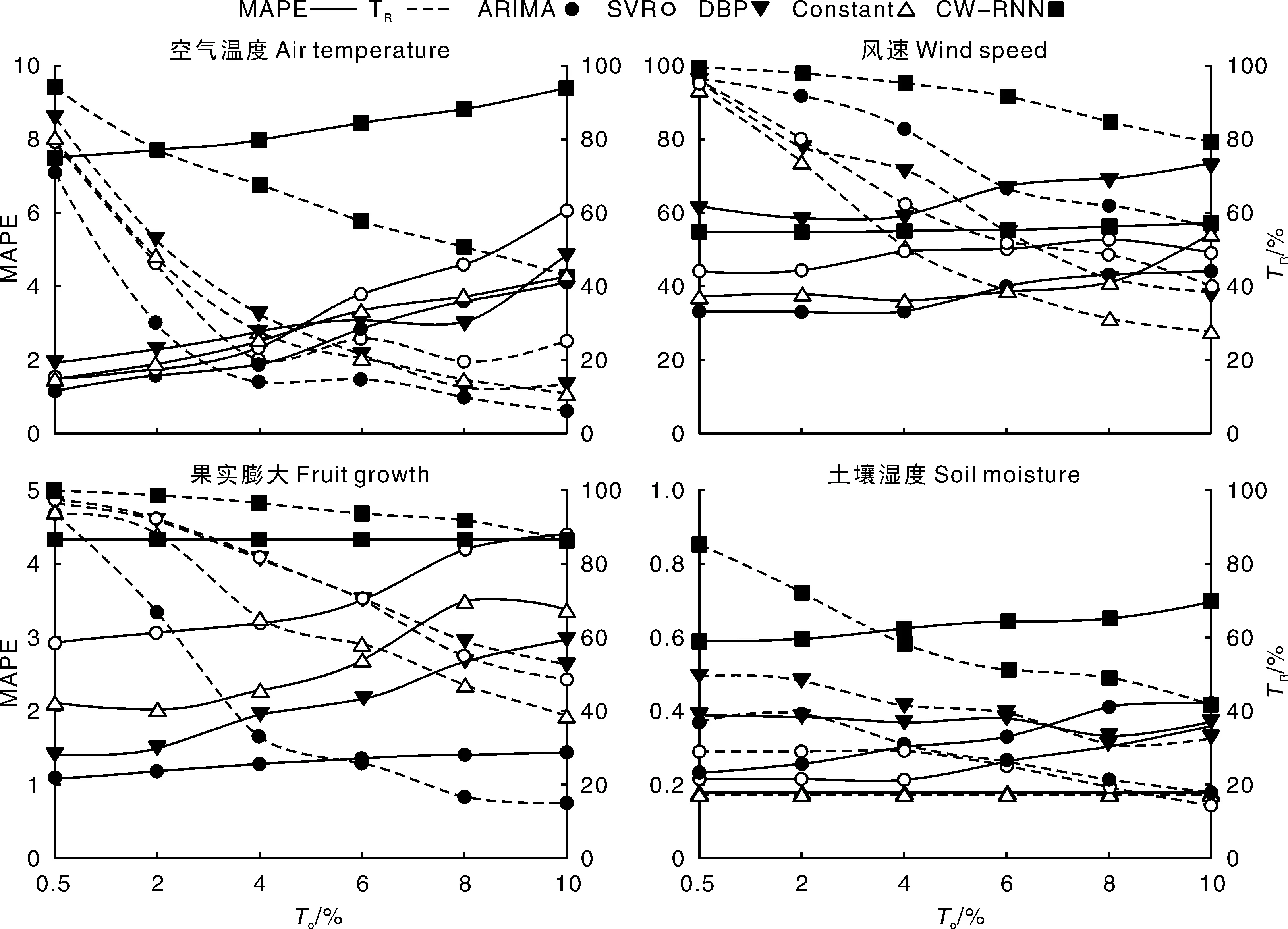
图4 不同误差容忍度下MAPE和业务数据传输率Fig.4 MAPE and data transmission ratio with different error tolerance

评价指标包括数据采集误差、业务数据传输代价、模型训练、模型更新和模型预测代价。如图2所示，网关/服务器端承担模型训练任务，将训练后的模型/参数发送至各传感器节点，故适用性评估过程中排除模型训练代价。适用性评估过程中数据预测误差采用前文所述的MAPE，业务数据传输代价定义为实际业务数据传输率。特别地，模型更新代价由模型更新所引起的数据传输量决定，而模型预测代价取决于算法执行数据预测的时间复杂度。如式(14)所示，综合一天数据采集过程中模型更新与预测代价定义模型运行代价(Fc)：

(14)

式(14)中：Ma为模型更新次数，Mu为模型更新所需传输的数据量，Bw为网络带宽，Dc为模型预测所消耗的平均时长。

如表1所示，模型间的更新内容及数据量存在较大的差异。ARIMA模型中，模型更新需要传输自回归系数φi和移动平均系数θj。DBP模型更新需要传输斜率α和截距β。机器学习模型SVR和CW-RNN需要传输完整的训练模型。Constant不需要传输任何模型/参数。

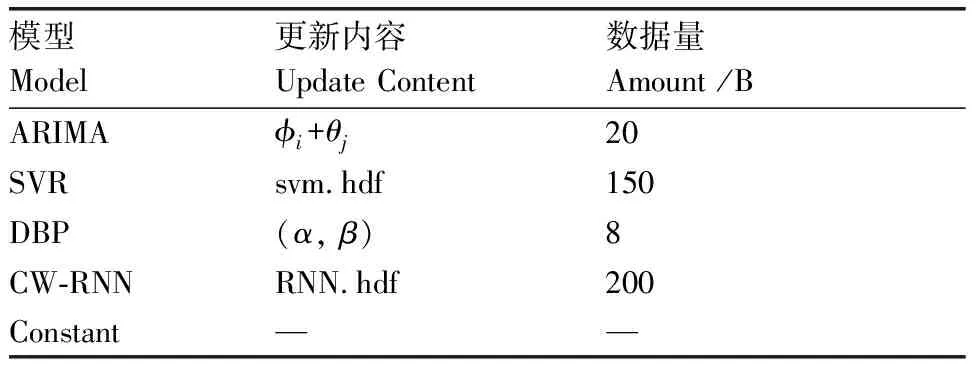
表1 模型更新内容及数据量

模型采用Python 2.7语言编写，硬件平台为具有1.2 GHz四核ARMv8处理器、1 GB内存的树莓派3代B型。预测长度为1，各模型的误差容忍度取其处理4类数据时的误差容忍度区间中值。考虑7、50、250 Kb·s-1和1 Mb·s-1等4种带宽，分别对应于低速率广覆盖物联网技术SigFox、LoRa、NB-IoT和LTEeMTC标准[20]的典型服务带宽。表2给出了空气温度数据的误差MAPE、业务数据传输率TR和模型运行代价F等3项指标值。

表2 空气温度评价指标

图5表示的是4种模型适用性评估结果对比。不同带宽条件下，模型优劣有差异。如空气温度指标，低带宽时模型优先级由高到低为ARIMA>DBP>Constant>SVR>CW-RNN，高带宽时模型优先级由高到低则为Constant>DBP>SVR>ARIMA>CW-RNN。这是因为优先级由数据收集误差、业务数据传输代价、模型更新和模型预测代价等因素共同决定：在小于250 Kb·s-1的低速带宽环境下SVR和CW-RNN远劣于ARIMA、DBP和Constant；当带宽为1 Mb·s-1时，ARIMA优势明显下降，仅优于CW-RNN。究其原因：ARIMA的优势在于较高的预测精度、低业务数据传输率和模型更新次数。如表2所示，ARIMA模型的数据采集误差MAPE和业务数据传输比分别为1.2571和13.89%，明显低于SVR的1.4229和20.14%。然而，ARIMA的预测代价约为SVR的9倍，模型更新次数及数据量少的优势随着带宽的增加被削弱，而模型预测计算时间对模型贴近度值影响程度增加，故ARIMA的贴近度甚至低于SVR。

总之，受制于较高的模型更新传输代价，SVR和CW-RNN不太适合于传感器节点数据收集预测模型。特别地，由于高昂的计算代价，CW-RNN难以在硬件资源受限的传感器节点运行。尽管SVR计算复杂度低，但高模型更新代价是制约其应用的关键因素。相比之下，ARIMA、DBP和Constant更适合用于传感器节点的数据预测。值得注意的是，得益于其较高的预测精度，ARIMA模型能在满足低传输率时实现较低的数据收集误差。然而，受到其高计算代价的影响，传感器节点运行ARIMA算法需要消耗更多的资源，且随着带宽的增加，优势逐步下降。进一步横向比较，可得出风速、土壤湿度等振荡型数据，Constant模型始终最优，DBP模型次之。对于光滑度较好的空气温度和果实膨大数据，DBP、Constant也有着较高的性能，且随着带宽的增加优势越发明显。故可得出：若节点同时具有较高的运算能力与通信带宽，除CW-RNN外的算法都可以考虑，具体优先级与实际运算和通信能力有关。若节点运算能力受限，DBP、Constant均较为合适，但考虑到模型同步的时滞性，采用Constant模型是较优的折中方案。

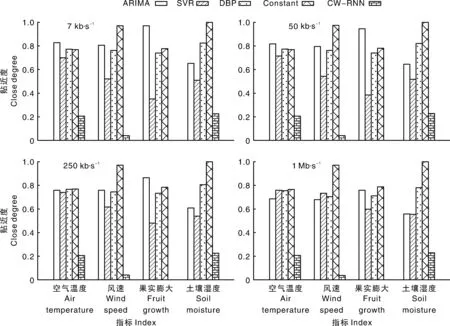
图5 不同预测模型的适用性评估结果对比Fig.5 Suitability comparison among different prediction models

3 结论与展望

如何甄选与应用数据预测模型，实现田间数据的高效压缩采集是农业物联网研究中一项非常有意义的工作。本文研究表明：对于空气温度、土壤湿度、果实膨大和风速等数据，ARIMA、SVR、DBP和CW-RNN等模型的最佳训练参数取决于模型机制和数据对象，各模型的适宜训练长度依次为9、5、6和72，误差阈值可设置为前期获取数据最大与最小值之差的2%～15%。综合考虑模型适用性与同步的时滞性，模型的适用性依次为Constant、DBP、ARIMA和SVR。受制于高计算复杂度和模型更新代价，CW-RNN不适合用于数据压缩采集。未来工作中，将进一步优化模型训练参数和误差阈值设置方法，探索压缩感知与模型驱动的融合策略以降低节点采样频率，为实现农情数据的高质量、低代价采集提供参考。