常利率下带干扰的复合Poisson-Geometric风险模型的期望折现罚金函数
2018-12-29李学锋郭仲凯
李学锋,郭仲凯
(中南民族大学 数学与统计学学院,武汉 430074)
1930年Cramer提出的经典风险模型为风险理论奠定了重要的基础,使风险理论得到广泛的研究,主要研究保险事务中各种随机风险模型的破产概率或生存概率. 但随着社会经济和保险市场的逐步发展,经典风险模型已经不能满足现代保险业务的需求了,于是许多学者对其进行了改进和推广.文献[1,2]研究了相依风险模型在有限时间内破产概率的渐近表达式.文献[3]得到了生存概率满足的积分-微分方程.在文献[4]中,Gerber和Shiu提出的期望折现罚金函数是现代风险理论研究的热点问题,该函数将破产时刻、破产前瞬时盈余和破产时的赤字融入到一个函数中,这一重要的函数为研究破产理论带来很大的方便,根据它可以得到一些具体的精算指标,推动风险理论向前发展.文献[5,6]得到了常数利率下经典风险模型的期望折现罚金函数满足的积分-微分方程及指数索赔下破产概率的表达式.文献[7]研究了复合Poisson过程风险模型的期望折现罚金函数、破产前瞬时盈余的Laplace变换、破产时刻以及破产时赤字满足的积分方程.文献[8-10]针对不同情形,选择了不同形式的期望折现罚金函数并研究了破产概率.
本文就是在上述工作的基础上,讨论一类在常数利率下带随机干扰的风险模型,其中保费收入是时间的线性函数,索赔过程为复合 Poisson-Geometric过程,得到了期望折现罚金函数所满足的积分-微分方程,然后根据该方程给出破产概率所满足的积分-微分方程并得到其在指数索赔下的特殊形式,同时还得到破产时赤字的概率分布函数所满足的积分-微分方程.
1 预备知识
定义1 设λ>0,0≤ρ<1,称{N(t),t≥0}是参数为(λ,ρ)的Poisson-Geometric过程,如果满足:
(1)N(0)=0;
(2){N(t),t≥0}具有独立平稳增量;
(3)对t>0,有N(t)~PG(λt,ρ).
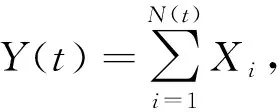
性质如果随机变量X~PG(λ,ρ),则当0<ρ<1时,X的概率分布为:
P(X=0)=e-λ,
[λ(1-ρ)]jρk-j,k=1,2,….
注定义2中的ρ称为偏离参数,刻画事故发生次数与索赔次数的差异.当ρ=0时,Poisson-Geometric过程即是Poisson过程.
2 模型介绍
定义3 设(Ω,F,P)是完备的概率空间(本文所有的随机变量都定义在此空间),则对u≥0,t≥0,保险公司在t时刻的盈余为:
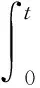
(1)
其中R(t)=ct-S(t)+σW(t),c为保险公司单位时间内收到的保险费,S(t)为索赔过程,{W(t),t≥0}为标准Wiener过程,表示保险公司不确定性收益和支出,σ>0为扰动系数,u≥0为保险公司的初始准备金;δ≥0为常数利率.
对上述模型做如下假设:
(2){Xi,i=1,2,…},{N(t),t≥0},{W(t),t≥0}相互独立.
易知风险模型(1)可写为:
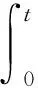
(2)
定义4 保险公司的破产时刻T=inf{t:t≥0,U(t)<0}(若集合为空集,则T=∞).
定义5 定义在[0,+∞)×[0,+∞)上的非负可测且依赖于破产前的盈余和破产时赤字的函数ω(x,y)称为罚金函数.
令I(E)为事件E的示性函数,U(T-)为破产前的瞬间盈余,|U(T)|为破产时的赤字,r≥0为折现因子,则称
φ(u)=E[e-rTω(U(T-),|U(T)|)I(T<∞)|
U(0)=u]
(3)
特别地,当ω(x,y)=1,r=0时,φ(u)为破产概率,即:
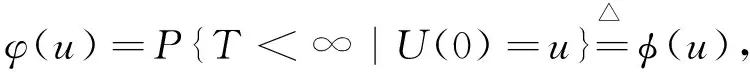
(4)
当ω(x,y)=x,r>0时,φ(u)为破产时刻瞬间盈余的期望折现函数,即:
φ(u)=E[e-rTU(T-)I(T<∞)|U(0)=u],
(5)
当ω(x,y)=y,r>0时,φ(u)为破产时赤字的期望折现函数,即:
φ(u)=E[e-rT|U(T)|I(T<∞)|U(0)=u].
(6)
3 主要结果及证明
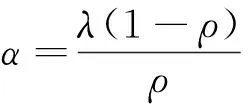
P{N(t)=0}=e-λt=1-λt+o(t),
P{N(t)=k}=αρkt+Ak(t)o(t),k=1,2,…,
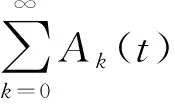
汉江是汉朝的发祥地。楚河汉界,不仅仅是历史的地域切割,是文化的融合。“大汉民族”、“汉文化”、“汉学”、“汉语”这些名称,得名于汉江。历史学家吕思勉和钱穆认为,华夏族就是生活在华山以南、夏水两岸的民族。而古代华山就是现在的河南嵩山,夏水就是今天的汉水。这说明,汉水流域是中华民族最古老族源的发祥地。


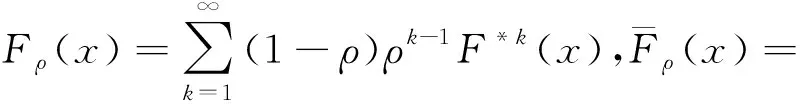
定理对任意u≥0,风险模型(1)的期望折现罚金函数φ(u)满足如下积分-微分方程:
(7)
证明令
在充分小的时间段(0,t]内,考虑(1)式所定义的风险过程U(t),根据是否发生索赔,分为两类事件:
事件B1:在(0,t]内没有索赔发生,即B1={N(t)=0},其发生的概率为:
P(B1)=e-λt=1-λt+o(t);
事件B2:在(0,t]内有k次索赔发生,即B2={N(t)=k},其发生的概率为:
P(B2)=αρkt+Ak(t)o(t),k=1,2,….
由盈余过程的强马氏性和全期望公式有:
(8)
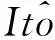
由引理知,(8)式中各项级数均一致收敛,由单调收敛定理,求和号与积分号可交换次序,故
(9)
进一步整理得:
(10)
将ert=1+rt+o(t)代入上式并两边同时除以t,令t→0,化简得:

即(7)式成立.
推论1 破产概率φ(u)满足如下积分-微分方程:
(11)
证明在(3)式中令r=0,ω(x,y)=1,则:
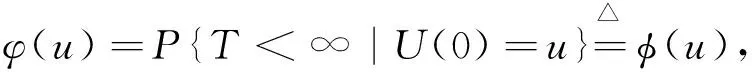

再由(7)式即得(11)式.
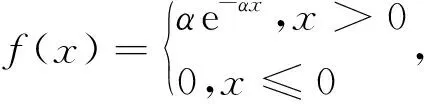

(12)
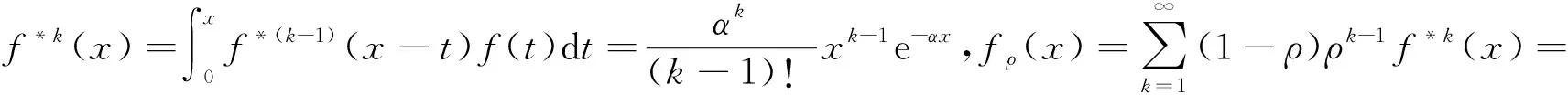
(1-ρ)αe-α(1-ρ)x.
令z=u-x,则:


从而有:

即(12)式成立.
推论3 破产时赤字|U(T)|的分布函数满足如下积分-微分方程:

(13)
证明在(3)式中令r=0,ω(x,y)=I(y≤v),则:
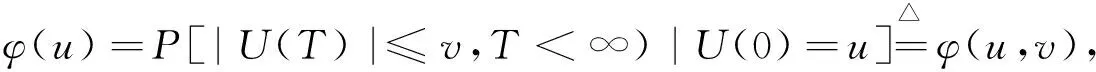

故(7)式可写为:

即(13)式成立.
4 结束语
本文从现代保险公司的实际运营情形出发,提出了常数利率下带随机干扰的复合Poisson-Geometric风险模型,具有较强的实际意义.利用概率论和随机过程等学科的理论方法得到该风险模型的期望折现罚金函数以及破产理论中的几个主要精算指标所满足的积分-微分方程.这些结果对保险公司解决破产概率等问题提供了理论参考,为保险公司设计相应的财务预警系统和保险监管部门设置相应的监管指标系统提供理论依据.当然,现代保险公司的实际经营运作情况往往更加复杂,本文所建风险模型乃至现有的所有风险模型都还有待进一步改进,本文的思想和方法在一定程度上为以后的研究提供了有益的思路.
