补贴政策对集装箱公铁联运竞争力的影响分析
2018-12-28唐继孟
唐继孟,李 建,阳 波
(1.湖南工业大学交通工程学院,湖南株洲412007;2.湖南省交通科学研究院有限公司,长沙410015;3.湖南省建筑设计院有限公司,长沙410012)
0 引 言
目前交通运输领域关于补贴政策的研究中,客运方面主要集中在公共交通补贴方面[1-2],货运方面主要集中在多式联运补贴方面.关于多式联运补贴方面的研究国外文献较多,而国内较少.Pekin[3]、Macharis等[4]都基于LAMBIT模型分析了补贴政策对多式联运发展的促进效果,发现促进效果明显.另外,Santos等[5]采用混合整数规划模型对比利时的多式联运补贴政策进行相关研究,结论表明,补贴政策促进效果明显,若废除比利时当前的补贴政策将造成多式联运终端货流减少40%.张戎等[6]以蚌埠—上海铁路集装箱运输链为研究对象,构建了多项Logit模型,研究补贴政策对铁路分担率的影响,结论表明,若取消目前的补贴,铁路分担率从现在的72.5%降到0.9%.
根据不同依据将既有研究分类:第1类根据补贴政策的研究方法可分为两种,一种是基于多式联运网络构建规划模型研究补贴政策[5,7-8],另一种是基于单个OD对采用离散选择模型来研究补贴政策[6,9-10];第2类根据补贴对象可以分为,补贴托运人的政策[5-6,8-11]和补贴承运人的政策[7,11].
本文研究的补贴对象为托运人,另外目前关于集装箱公铁联运补贴政策的研究大多从托运人角度出发,采用离散选择模型进行研究,未从系统角度出发,考虑政府部门、铁路公司和托运人相互作用机理,对补贴政策的作用机理研究尚有不足.因此,本文首先分析了补贴政策下政府部门、铁路公司和托运人三者间的相互作用机理,然后构建了双层规划模型,用于深入研究补贴政策的作用效果.
1 问题描述与建模
1.1 补贴政策作用机理描述
补贴政策的作用机理如图1所示.政府部门根据货物运输过程中由铁路完成的货物周转量大小,对托运人进行补贴.政府部门的补贴政策会影响托运人的选择行为,而其选择行为改变后,铁路公司的货运量也会发生改变,从而影响铁路公司集装箱班列的开行方案,铁路公司的开行方案调整后,又会反过来影响托运人的选择行为.同时,铁路公司完成的货物周转量直接决定了政府部门的补贴金额.因此,这三者之间相互博弈,最终达到一个平衡状态.
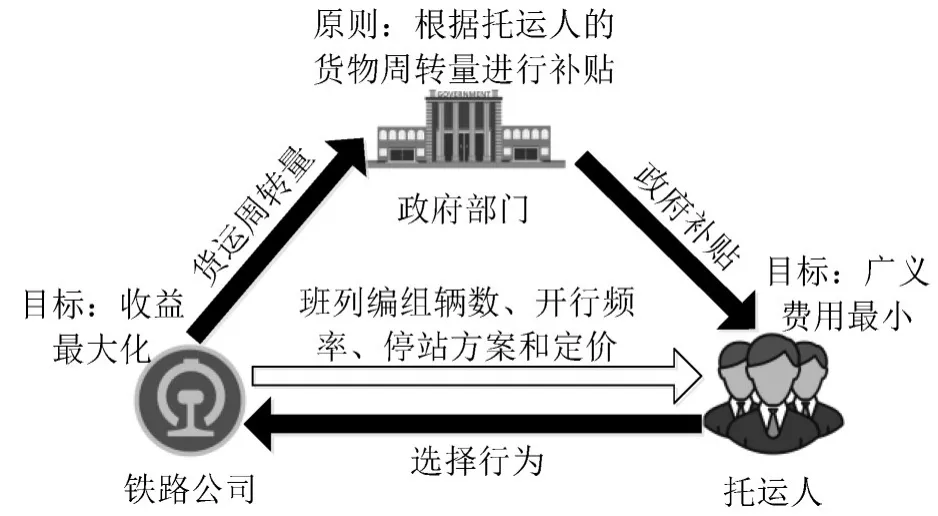
图1 补贴政策的作用机理Fig.1 The mechanisms of the subsidy policy
1.2 建模基础
考虑到公铁联运网络中铁路运输弧具有“周期连接(Periodic Connectivity,PC)”和“速度异步改变机制(Asynchronous Change of Travel Speed,ACTC)”特性,本文分别通过网络拓展和定义分段阻抗函数来处理这两类特性.
(1)网络拓展.
公铁联运网络中,公路弧是一种“基础设施通道”,用户可以随时使用;而铁路弧是一种“基础设施+列车”的服务通道,即2个站之间有班列开行时,2个站之间的弧才是连通的,否则不通,这就是铁路弧的PC特性.为了表达铁路弧的PC特性,可以将物理网络拓展为时空网络[7],如图2所示.
根据图2(a)所示的公铁联运网络拓扑结构,添加时间轴,将1天离散为4个时间点(本文建模时离散为24个点),拓展为时空图(图2(b)所示);再根据节点之间连接关系,向时空图中添加带时间属性的公路弧、班列运行弧、小运转列车运行弧、等待弧、虚拟弧和虚拟节点.
(2)阻抗函数定义.
对时空图中各类弧的阻抗函数进行如下定义.
公路弧为
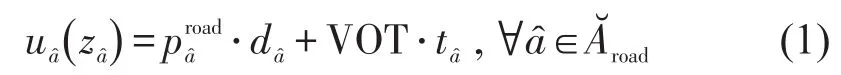
小运转列车弧为
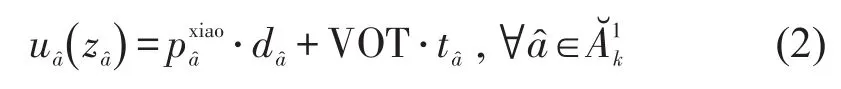
考虑到公铁联运网络中铁路弧存在ACTC特性,即当货物到达中心站或专办站时,如果班列已经装满货物,则需要等待下趟班列,因此,将铁路弧的阻抗函数定义为分段函数,即
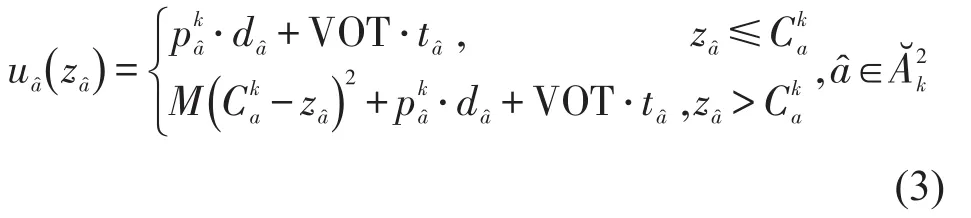
班列等待弧为
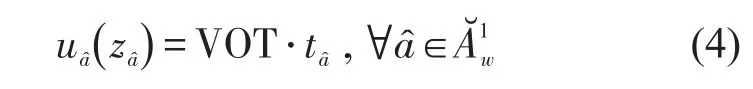
另外,虚拟弧的阻抗为0.
(3)模型涉及的变量参数定义.
①索 引.
a,â分别表示物理网络和时空图中弧的索引;k表示班列开行方案索引;r,s分别表示需求起、终点;h表示路径索引.
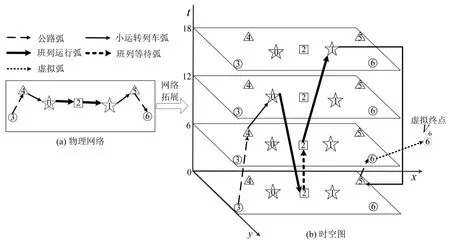
图2 网络拓展示意图Fig.2 The schematic diagram of network expansion
②决策变量.
ρk表示是否采用第k种班列开行方案,0表示不采用,1表示采用;mk和fk分别表示第k种班列开行方案的编组辆数和开行频率;表示第k种班列开行方案的班列停站方案,是N3维0-1向量,每个元素对应一个专办站或中心站,0表示不停,1表示停站;表示第k种班列开行方案中班列的发车时间,是24维的0-1向量,每个元素对应一个离散的时间点,1表示发车,0表示不发车.
③集 合.
N1,N2,N3分别表示物理网络中需求节点、办理站及专办站和中心站的集合;Aroad表示物理网络中公路弧的集合;分别表示物理网络中小运转列车运行弧和班列运行弧的集合;Groad表示物理网络中公路子网络;表示第k种班列开行方案对应的铁路子网络表示公铁联运物理网络;̂表示由拓展而来的时空图;̆分别表示时空图中公路弧、小运转列车弧、班列运行弧、等待弧和虚拟弧的集合;表示时空图中虚拟节点集合;表示时空图中所有节点的集合;B表示班列开行方案集合;Rrs表示时空图中r、s之间的路径集合.
④中间变量.
⑤参 数.
1.3 双层模型构建
(1)上层模型.
目标函数是铁路公司的利润率最大化,即
班列开行方案选择约束,保证有且只有一种方案被选择,即
公路弧的运输时间为
铁路弧(班列运行弧和小运转列车运行弧)的运输时间为
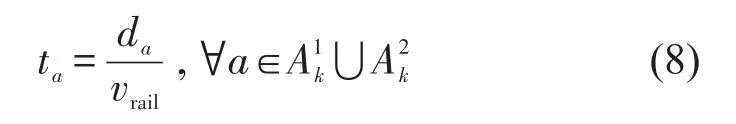
根据文献[12]可知,单列集装箱班列在运行区段a上的成本为
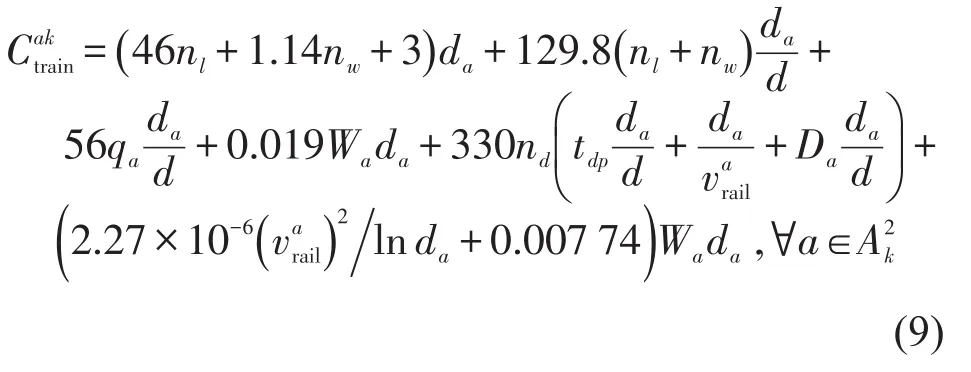
式中:d和da分别表示班列全过程运行距离和区段a的距离;qa和Wa表示班列在区段a上的载重和总重;tdp和Da分别表示司机的准备时间和区段a上的延误时间(本文都取0).
采用第k种班列开行方案时,班列运行弧a的单位成本为
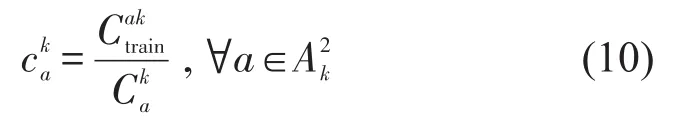
采用第k种班列开行方案时,铁路公司的总成本为
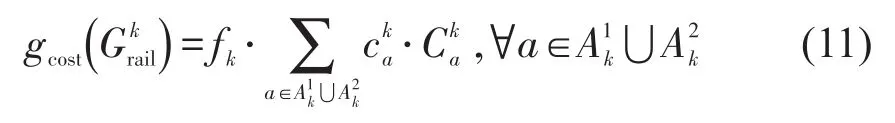
为了保证公铁联运网络的完整性,即使铁路公司亏损,也必须开行一定数量集装箱班列,且班列编组辆数一定,实际情况也是如此,特别是市场培育期.
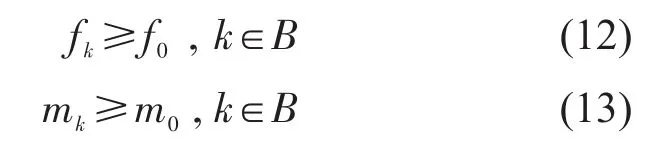
决策变量的定义域为
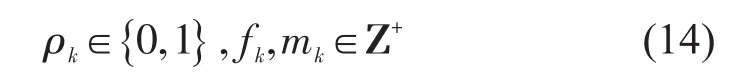
(2)下层模型.
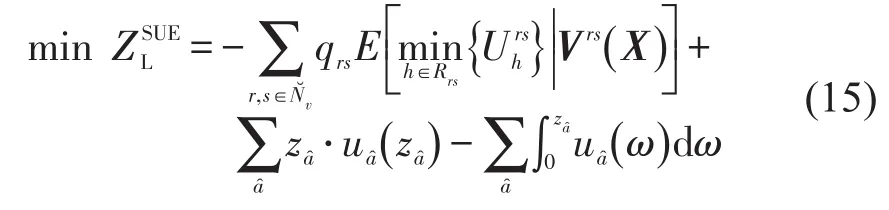
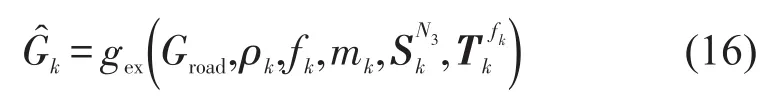
OD需求qrs与该OD之间路径流量之间的关系为
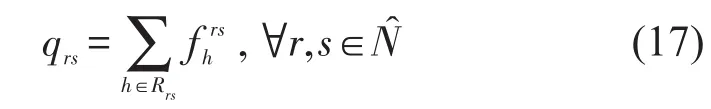
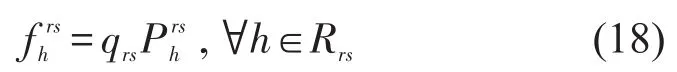
时空图中路段流量zâ与路径流量之间的关系为
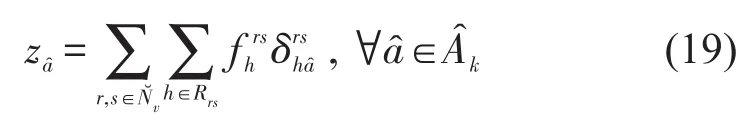
物理网络和时空图中铁路弧单位成本的对应关系为
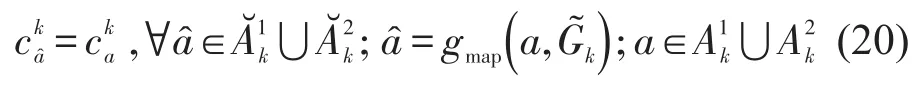
物理网络和时空图中小运转列车弧单位运价的对应关系为
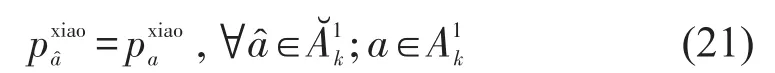
政府部门对托运人进行补贴,相当于降低了班列的价格(小运转列车运行弧的单价也相应的减少css),根据文献[7]的研究,本文采用的班列定价函数为
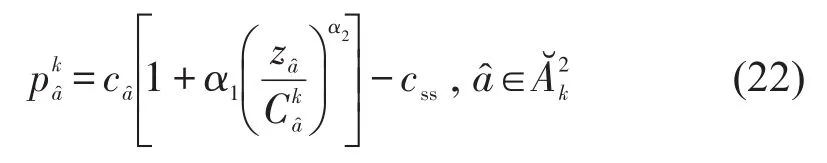
采用第k种班列开行方案时,铁路公司的实际利润如式(23)所示,分别包括集装箱班列和小运转列车的收益.
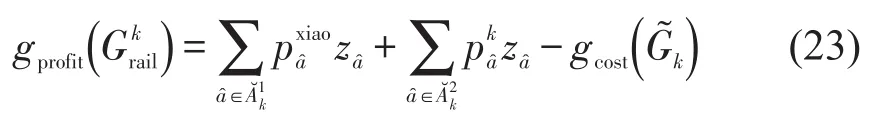
变量的定义域为

2 求解算法
针对上一节的双层规划模型,本文采用如图3所示的混合遗传算法进行求解,遗传算法用于求解上层模型,搜索最优的班列开行方案,而连续平均算法(Method of Successive Averages,MSA)用于求解下层随机用户最优模型.首先,初始化,即随机产生种群;接着,对种群Popn中的每个个体,将其与公路网Groad合并后,拓展为时空图,在该时空图上采用MSA算法求解下层的SUE模型,求解结果为各弧的流量zâ,并计算个体的适应度;然后,根据当前种群Popn中个体的适应度或迭代次数判断是否结束搜索,如果不结束,则通过选择、交叉和变异产生新的种群Popn,并重新计算每个个体的适应度,再次判断是否结束,如此循环迭代,直到算法终止.
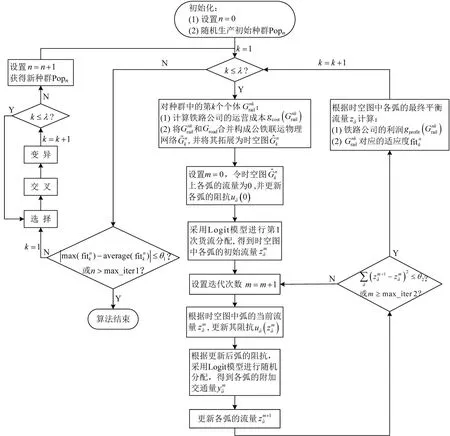
图3 混合遗传算法的流程图Fig.3 The flow chart of the hybrid genetic algorithm
参数取值:λ表示种群规模,取100;θ1,θ2分别表示遗传算法和MSA算法的收敛标准,都取0.1;k表示种群Popn中个体的索引;m和n分别表示MSA算法和遗传算法的当前迭代次数;max_iter1和max_iter2分别表示遗传算法和MSA的最大迭代次数,都取100.
3 算例分析
本文构建如图4所示的算例,某集装箱运输通道上,中心站0和3之间有2个专办站(1和2),中心站或专办站吸引范围内都有1个办理站,分别是4、5、6和7;另外还包括通道附近的9个需求节点,分别是8~16.需要说明的是本算例只研究中心站0~3这个方向的班列和集装箱货流,如表1所示.
基于上述算例,采用混合遗传算法求解本文的双层规划模型,得到不同补贴额度下铁路公司的运营成本、实际利润、政府部门的补贴金额和公铁联运分担率(竞争力),如图5所示.
由图5可知:
(1)随着补贴额度的增加,铁路公司的运营成本和政府补贴总金额呈“上升”趋势,而铁路公司的实际利润呈现“先降后升”的趋势,当补贴额度达到0.12元/(t⋅km)时,铁路公司开始盈利.补贴额度在0.00~0.06元/(t⋅km)时,尽管选择公铁联运的集装箱货流有所增加,但由于此时的货流较小,式(23)中成本比收入增加更快,出现“运得越多,亏损越多”的现象,因此在这期间铁路公司维持最低的班列开行频率和编组辆数.当补贴额度超过0.06元/(t⋅km)时,随着补贴额度继续增加,公铁联运的货流进一步增加,铁路公司的亏损开始减少.
(2)补贴额度增加的初始阶段(0.00~0.14元/(t⋅km)),提高补贴额度对公铁联运竞争力的提升效果明显,但是当补贴额度超过0.14元/(t⋅km)后,补贴额度继续增加时,公铁联运竞争力和铁路公司的实际利润增长缓慢,几乎没有变化.其原因是:当补贴额度超过一定值(本算例为0.14元/(t⋅km))后,补贴额度的增加使得公铁联运广义费用下降后,所带来的公铁联运竞争力提升效果越来越差,即转移到公铁联运的货流越来越少,从而导致公铁联运分担率和铁路利润变化不大.
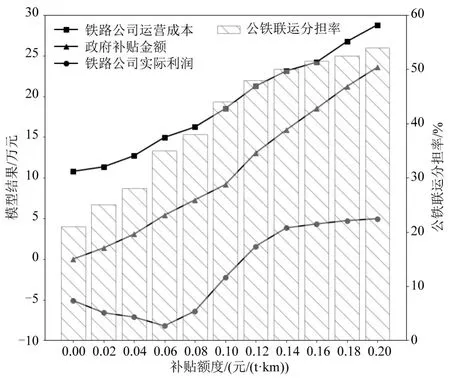
图5 不同补贴额度下的模型结果Fig.5 The results of the model in different subsidies
与既有研究[5-6,9]进行比较可知(如图6所示):相对于既有研究中基于单个OD对,采用Logit模型分析补贴政策对公铁联运竞争力的影响[6,9],本文研究结论表明随着补贴额度的增加,公铁联运竞争力并非迅速上升,而是趋于平缓.
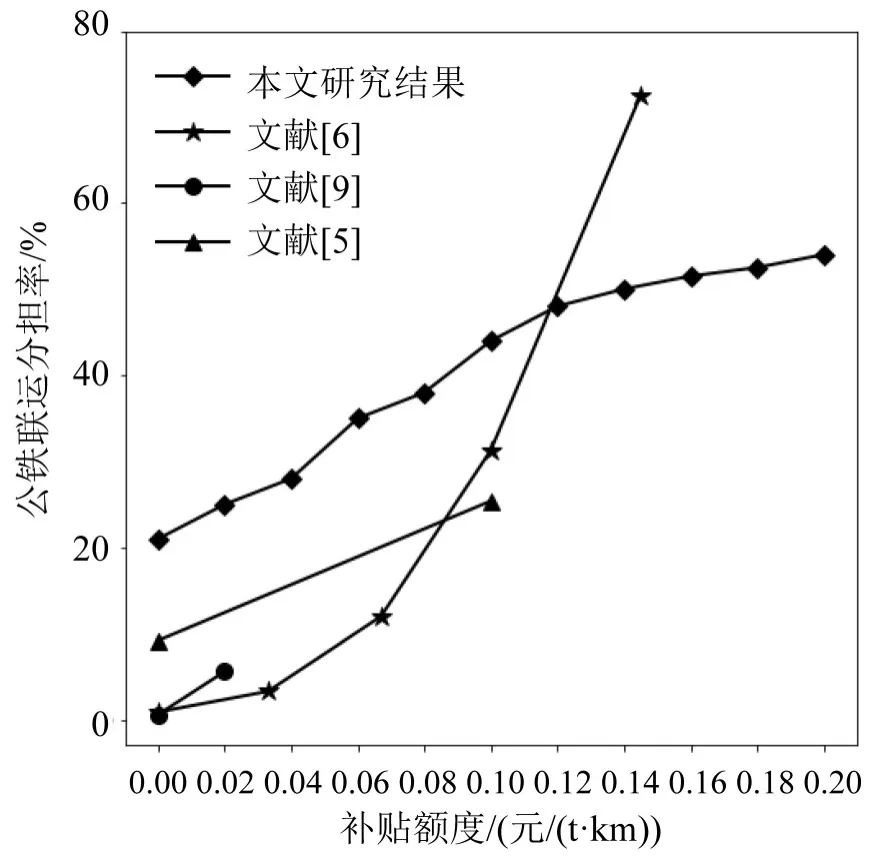
图6 与既有研究结论对比Fig.6 Comparing our conclusions with existing researches'
既有研究可能高估了补贴政策的影响效果,其原因主要有两方面:一是本文与文献[5]的研究是基于公铁联运网络的,涉及多个OD对,不同OD对的铁路运输距离和公路接驳距离有所差异,对补贴政策的反应也不一样,不同效果平均后,可能就没有单个OD对那么明显;二是补贴政策对公铁联运的影响,并不是降低公铁联运广义费用后,托运人1次重新选择的结果,而是如本文1.1节所描述的“政府部门、铁路公司和托运人3者之间相互作用后达到的一种平衡状态”,另外,相互作用过程中,铁路公司的班列定价策略会抑制补贴政策的效果.
4 结 论
本文基于补贴托运人政策下政府部门、铁路公司和托运人之间的相互作用机理,构建了能够反映该机理的双层规划模型.上层模型描述了铁路公司根据货运量制定集装箱班列开行方案从而使自身利润最大化的行为;下层模型描述了托运人在政府补贴政策下的选择行为.基于双层规划模型的结构,本文构造了混合遗传算法,并用于求解本文的算例,其结果表明:补贴额度增加的初始阶段(0.00~0.14元/(t⋅km)),提高补贴额度对公铁联运竞争力的提升效果明显;但超过0.14元/(t⋅km)后,提升效果不显著,因此,当补贴额度达到一定值后,继续增加补贴额度意义不大.本文的研究结论与基于单个OD对采用离散选择模型的既有研究不同,该类既有研究高估补贴政策效果的主要原因有两个:针对单个OD的研究结论可能具有片面性,以及离散选择模型未能真实地反映补贴政策的作用机理.
