快速路出口衔接过饱和交叉口信号优化方法
2018-12-28杨晓光
张 楠,杨晓光
(同济大学道路与交通工程教育部重点实验室,上海201804)
0 引 言
城市快速路与其周边区域衔接道路的拥堵是城市交通拥堵的一个主要问题.不同于一般的城市道路,在快速路出口匝道区域,快速路交通流以较高的流量持续到达与地面道路高峰交通流构成了较大的交通需求;另一方面,由于下游交叉口控制信号的存在,道路通行能力受到限制,特别是当地面道路的空间有限,进一步限制通行能力的提升空间.因此,在高峰期内,出口匝道衔接区域的交通需求大于通行能力,出现过饱和交通状态.出口匝道车辆排队经常发生溢出,进而造成快速路主线车流的拥堵,并向上游蔓延.
当地面流量较小时,为防止出口匝道排队溢出,可根据匝道是否发生溢出决定在下游交叉口实施优先控制,使该方向排队及时消散[12].地面流量较大时,利用交通信号控制,减少上游地面道路或者出口匝道的交通流流入,缓解交通流过饱和状态[3-5].考虑地面道路通行能力不足或者远小于上游交通需求的情况,该区域交通流的排队会迅速增长,并始终保持在饱和状态.所以,本研究在对该区域交叉口信号优化时即需要考察限制上游交叉口的交通流到达,同时需要增加下游交叉口的交通流消散,缓解过饱和状态,防止交通流溢出[6].
在出口匝道交通需求较大且无匝道控制的条件下,根据不同目标之间的相互关系,可选择建立两阶段优化模型[7]或者双层规划模型[8],优化基础信号周期和绿信比,最大限度的增加关键方向上的绿灯时间.在以上研究的基础上,本研究不仅需要优化基础控制方案,还需要在此基础上利用控制策略对基础控制方案的优化结果进行调整,使基础控制方案和控制策略方案同时最优.基于以上两个控制目标的上下层作用关系和双层规划的特点,本文选择双层规划模型(Bi-level Programming,BLP)建立优化模型[9].
1 问题提出
本研究中的快速路出口衔接区域是由城市快速路,快速路出口匝道,衔接地面路段,道路上下游信号控制交叉口组成的区域,如图1所示.其中衔接路段(断面3至断面4)为通行能力约束路段.在高峰时段,地面辅路到达的交通流(断面2)和快速路出口匝道到达交通流(断面1)大于下游衔接路段的通行能力.此时下游交叉口(断面5)每个周期的排队不能完全消散,处于过饱和状态.当排队蔓延到上游,造成断面1处的交通流溢出,阻塞快速路主线的交通流,同时断面2处的交通流不能及时消散.
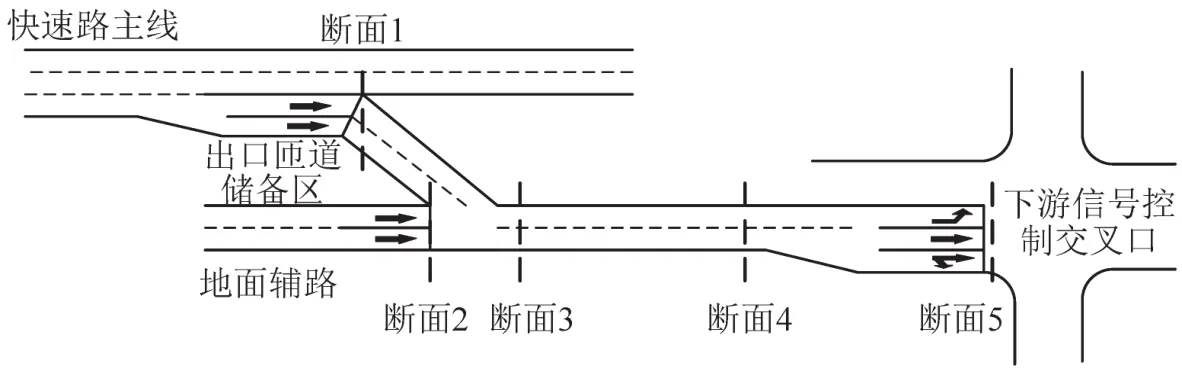
图1 快速路出口与衔接交叉口区域示意图Fig.1 Area of urban freeway off-ramp with connected intersections
本研究在断面1和断面2处设置控制信号,将其设置为1个信号交叉口,与下游信号交叉口组成该区域内的协调控制交叉口,通过优化上下游的交叉口控制信号方案,调节该区域内的交通流,防止匝道交通流溢出,缓解过饱和的交通状态.
本研究提出以下几点假设条件:
(1)在高峰时段内,快速路出口方向交通流为过饱和状态,其他方向交通流为常规状态.交通流到达相对稳定.
(2)高峰时段内采用定时控制,绿灯间隔时间为,黄灯时间3 s和全红时间1 s.
(3)断面1上游具备一定的物理空间,作为红灯时间内车辆排队的储备空间.
(4)断面2排队不影响上游交叉口.在现实条件下,可以将所有影响的相关交叉口包括在研究区域内.
本研究符号含义说明如表1所示.
2 出口匝道与衔接交叉口信号优化的BLP模型
根据BLP模型的特点[9],本研究将控制信号中的绿灯时长和红灯时长作为下层规划的决策变量,将信号方案绿灯和红灯调整时长作为上层规划的决策变量.利用下层规划模型实现对区域内单点交叉口的控制信号优化,同时利用上层规划模型实现上下游交叉口控制信号调整方案优化,并且考虑通行能力的限制为上层规划的约束条件.

表1 符号与变量说明Table 1 Symbols and parameters
2.1 下层规划模型
2.1.1 下层规划目标函数
利用车均延误作为单个交叉口的信号方案优化目标函数[10].1个信号周期内,进口道排队完全消散的延误如图2(a)所示,其计算公式为
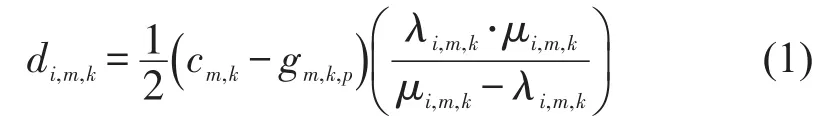
为保证快速路主线车流不受出口匝道排队影响,每个周期匝道排队需要完全消散.
1个信号周期内,进口道排队无法消散,如图2(b)所示,处于过饱和状态的延误为
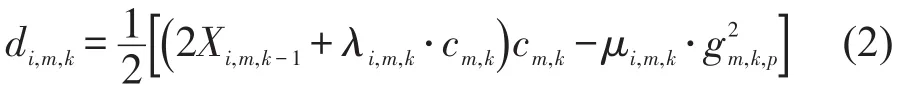
其中:
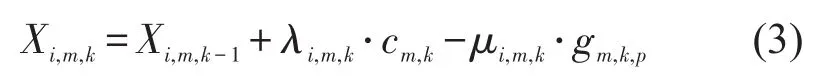
下层规划模型的目标函数为全部交叉口高峰时段内车均总延误最小,即
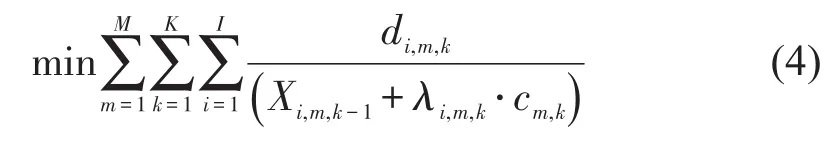
2.1.2 下层规划约束条件
每个周期出口匝道最大排队不超过断面1上游储备区域的最大排队数,即
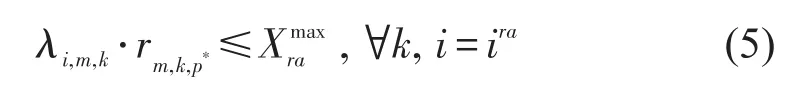
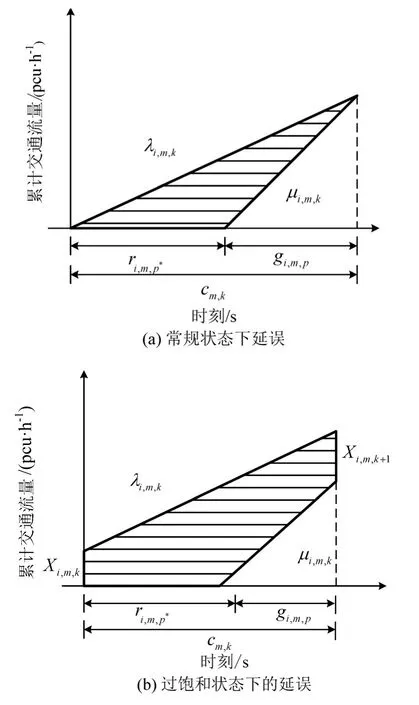
图2 进口道延误计算Fig.2 Approach delay
在同一个周期中,进口道绿灯相位p*时长等于非该进口道绿灯相位时长(用/p表示)的总和.此外,绿灯和红灯时长应满足最大和最小约束.
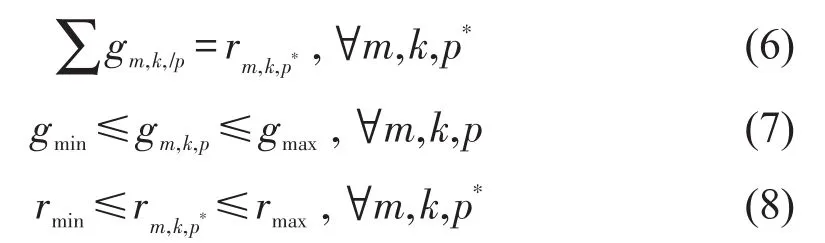
2.2 上层模型
2.2.1 上层规划目标函数
对于本研究的问题,交通流过饱和流向的上下游信号控制相关联的是断面1,断面2和断面5处的控制信号.对该方向上的相位时间的调整策略包括[6]:
策略I减少过饱和方向上游绿灯相位时长,可以减少上游交通流量的流入.当某一时刻断面3发生溢流现象,断面1的绿灯失效,需要减少断面1的绿灯时长,控制进入约束路段的流量,如图3(a)所示.此时断面1的绿灯时长为.策略I的上层规划目标是断面1交通流自由通过的时间最大化.为了不影响快速路主线交通流,断面2的信号相位不做调整.
策略II减少过饱和方向下游交叉口红灯相位时长,使排队提前消散,防止排队溢出.如图3(b)所示,断面5在红灯相位开始后经过发生溢流,经过溢流排队消散,此时减少红灯时长防止溢流.由于减少红灯时间会减少其他进口道绿灯时间,所以策略II上层规划的目标是最小化减少红灯时长.
策略III延长过饱和方向下游交叉口绿灯相位时长,最大限度的降低绿灯结束时的排队长度,使,如图3(c)所示.为了使断面5处的车辆尽可能的消散,所以策略III上层规划的目标是最大化延长绿灯时长.
以上问题上层规划的目标函数为
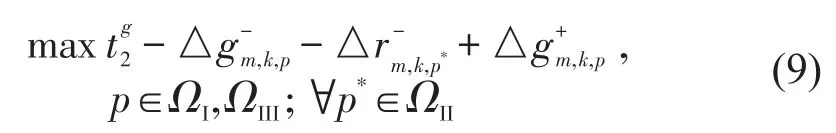
其中:
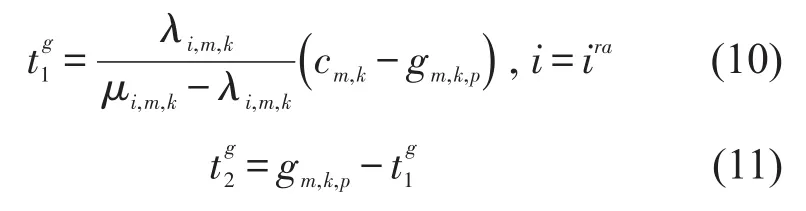
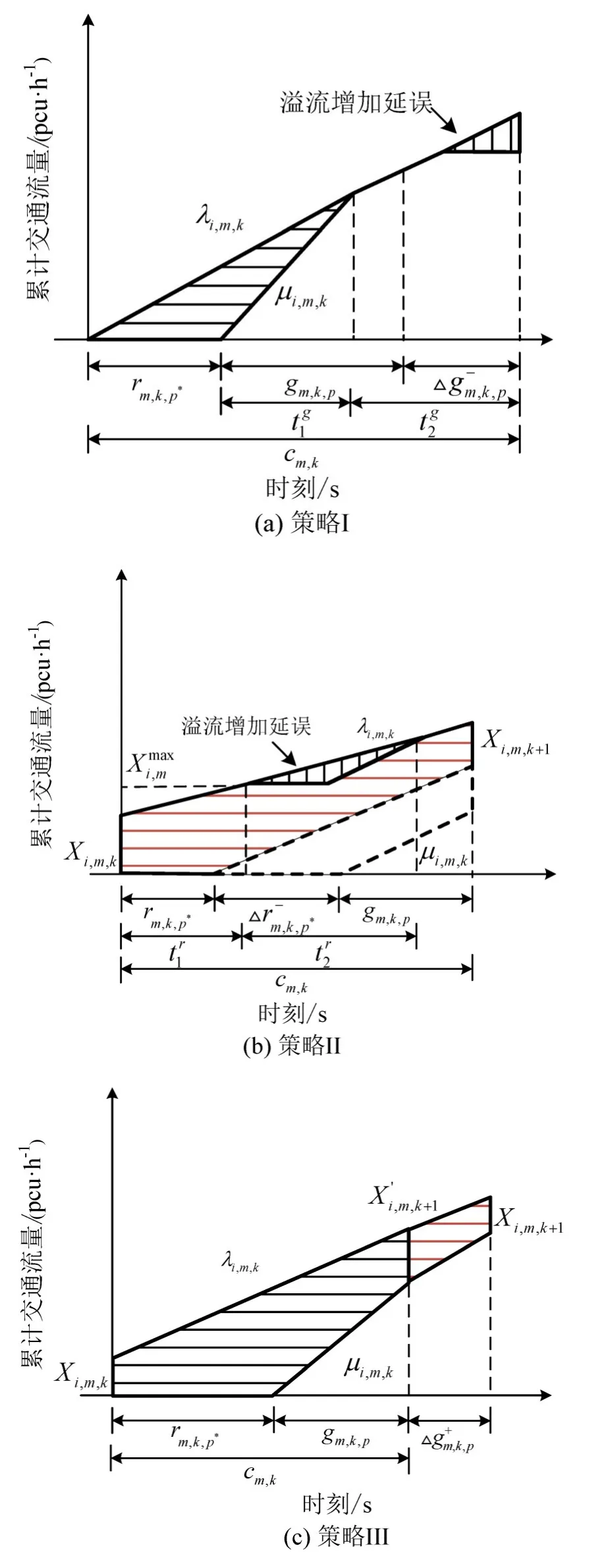
图3 控制策略调整时长Fig.3 Adjustment signal timings of traffic control strategies
2.2.2 上层规划约束条件
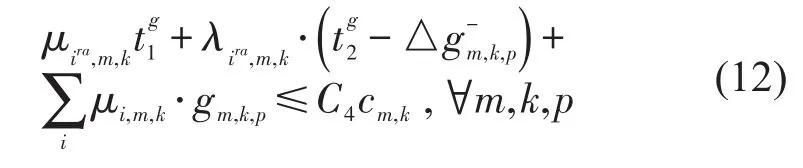
断面5的红灯时长调整后的最大排队长度小于排队最大值,防止排队在断面4处溢出.
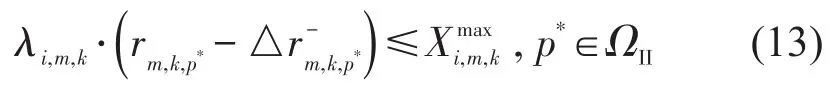
绿灯结束时,保证断面1的排队被清空,所以有
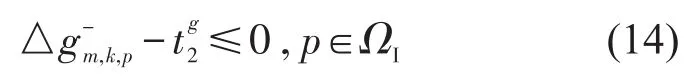
信号调整时长满足最大和最小限制,即
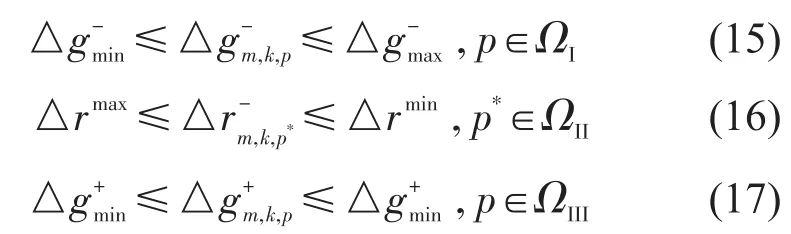
控制调整策略对下层规划的约束条件式(6)产生影响,其中属于策略集合的相位时长根据策略进行调整,其他相位保持不变.对于策略II,减少红灯相位p*时长等于减少非该方向的绿灯相位(用/p表示)时长总和.
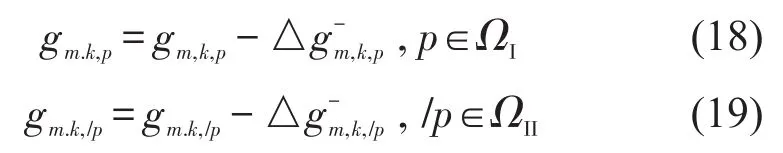
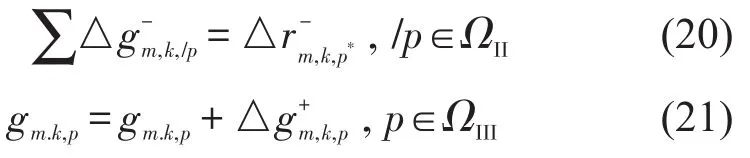
综上所述,本研究建立的BLP模型是:上层规划目标函数为式(9)~式(11),约束条件为式(12)~式(17);下层规划目标函数为式(4),约束条件为式(5),式(7),式(8),式(18)~式(21).本研究提出的BLP模型可以利用遗传算法进行求解[9].
3 模型实例验证与分析
3.1 实例简介
利用乌鲁木齐市东外环快速路与红山路相近的出口匝道周边区域作为实例,如图4所示.断面4和断面5之间的路段为通行能力约束的路段.断面1为快速路出口匝道,断面2和断面3为地面辅路和支路进口道.断面6是出口匝道方向下游交叉口停车线.该区域交叉口编号,道路条件等如表2所示.根据实际调查数据,该区域单车道饱和流量取值约为1 200(pcu·h-1).
在断面1至断面3设置控制信号作为上游交叉口并编号为2,下游交叉口编号为1.控制信号相位,如图5所示.设置绿灯,红灯和调整信号时长的取值区间,如表3所示.
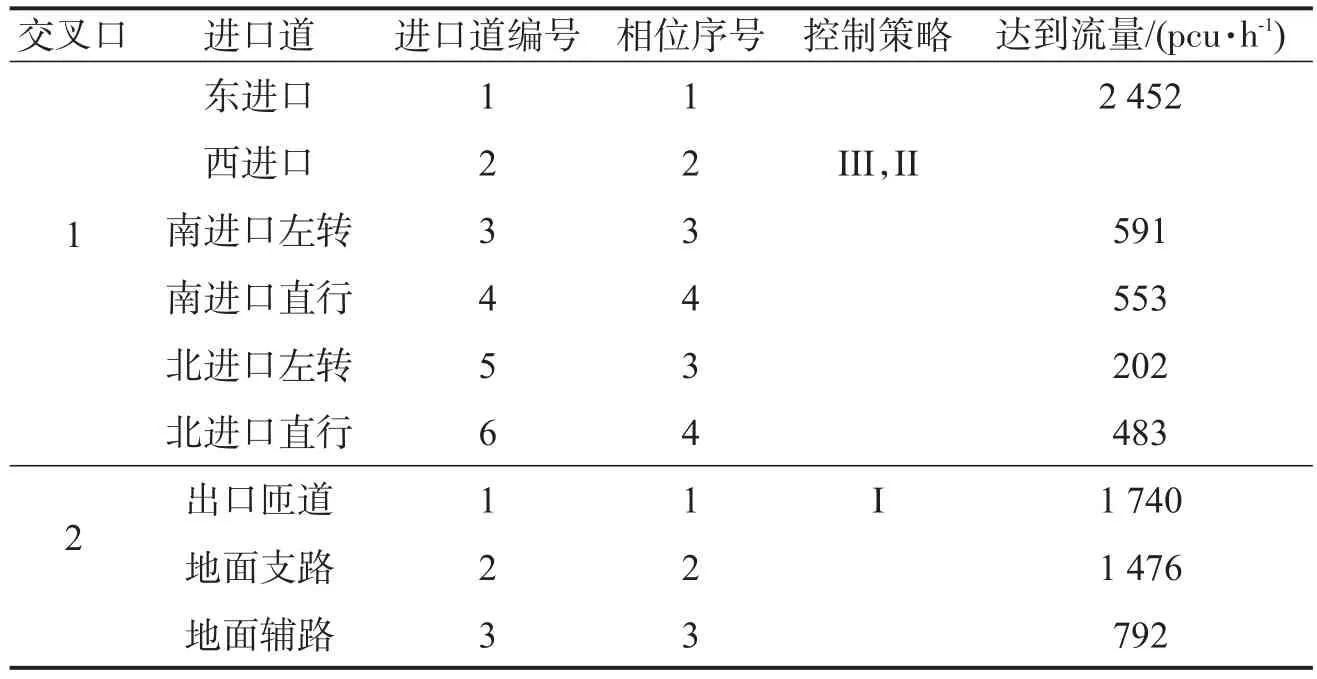
表2 实例分析中交叉口编号与数据Table 2 The number and data of the intersection in analysis example

表3 控制方案变量取值区间Table 3 Maximum and minimum signal timings of control plan (s)

图4 乌鲁木齐快速路匝道出口区域Fig.4 The area of unban freeway off-ramp in Urumqi
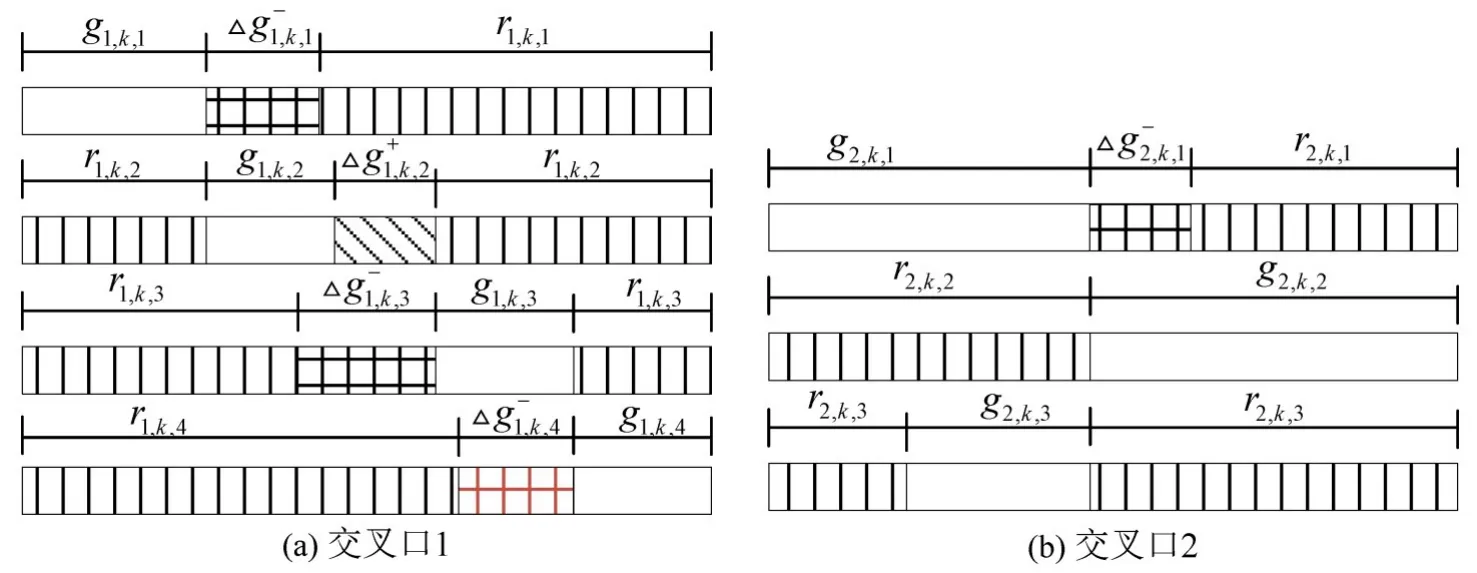
图5 信号控制相位Fig.5 The signal phases
3.2 BLP模型验证与结果对比分析
为了对BLP模型的结果进行分析,定义以下非线性规划(Nonlinear Programming,NP)问题.定义NP模型是目标函数式(4),约束条件为式(5)~式(8),式(13)和式(14)组成的模型.模型NP不计入调整时间变量.将以上的数据代入模型,利用遗传算法计算NP和BLP模型的最优信号方案,如表4所示.

表4 最优化信号绿灯与周期方案Table 4 Optimal green and cycle timings of signal plans by NP and BLP (s)
利用Vissim仿真对以上优化信号方案进行测试分析.相同的路网条件和交通流量到达情况下,对出口匝道和衔接地面道路无信号控制(下游交叉口1信号方案采用现状配时方案),设置信号控制分别采用NP和BLP方案进行测试.统计高峰期1 200 s内40个时段过饱和交通流方向上断面平均排队长度,如图6所示.
由图6可知,当上游不设置控制信号时,由于通行能力有限,断面5的排队延伸至上游,阻碍了断面1和断面2的交通流消散,断面1排队溢出,引起快速路主线拥堵.设置控制信号之后,NP和BLP控制方案缓解了断面5的过饱和状态,防止了断面1的排队溢出.但是由于衔接路段通行能力的限制,控制方案加重了断面2的过饱和状态.
BLP和NP模型最优控制信号方案下的延误,如表5所示.在出口匝道和交叉口1西进口道的交通流方向上,BLP模型的信号方案比NP模型的延误增加,但是其他方向延误都相对降低,总延误也相对最小.
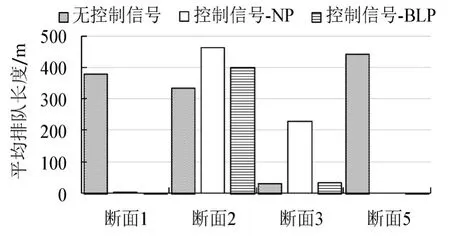
图6 控制信号方案排队长度仿真结果Fig.6 Simulation queue length results of signal control plans

表5 最优化信号方案的车均延误Table 5 Average delay values of optimal signal plans by NP and BLP
保持快速路出口匝道到达流量不变,地面支路到达交通流取值为0.22辆/s,0.33辆/s,0.41辆/s(算例)和0.56辆/s,代入NP模型和BLP模型计算后得到的结果对比如图7所示.由图7(a)可知,BLP模型的出口匝道绿灯时间均小于NP模型而且相对稳定.策略I减少上游出口匝道的到达流量的同时减少了地面支路红灯时间.随着地面支路流量与出口匝道流量逐渐接近,NP模型的优化结果趋于BLP模型.由图7(b)可知,因为交叉口1西进口的到达流量较大而且稳定,所以,红灯和绿灯时长也相对恒定.流量相对较低时,两个模型的结果近似.但是随着流量增大时,策略II使得BLP的红灯时间小于NP模型.另一方面,策略III延长绿灯时长后也相对小于NP模型的绿灯时长,对其他方向的交通流更为有利.所以,该区BLP模型优化的域内的车均总延误总小于NP模型,如图7(c)所示.
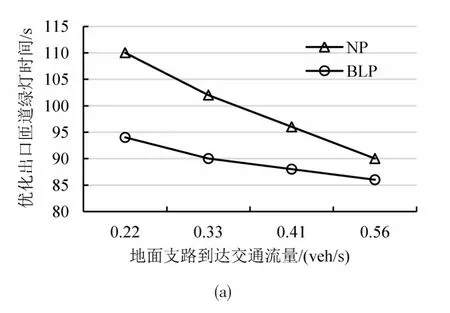
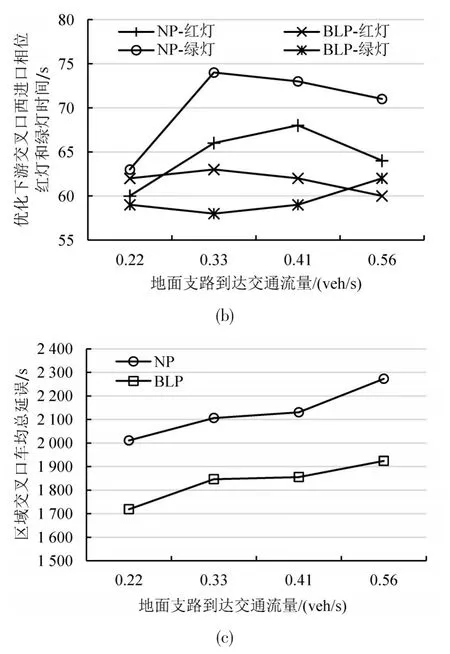
图7 不同地面道路到达流量条件下优化结果对比Fig.7 Comparison of optimization results under different surface road traffic flow rate
4 结 论
针对本研究提出的问题,建立BLP模型优化该区域交叉口控制信号方案和信号控制策略方案的结论为:
(1)BLP模型优化结果可以有效防止匝道交通流溢出,避免快速路主线交通的拥堵.但是由于通行能力限制,同时会对地面道路其他方向的交通流产生不利影响.
(2)相对于常规NP模型只对基础控制方案优化,同时对控制策略方案优化的BLP模型优化的信号方案不会过度的将信号分配给快速路出口匝道方向,能够相对减少其他方向交通流的延误和排队.在通行能力约束的条件下,BLP模型优化的信号方案提升系统整体性能上更为有效.
