考虑车辆尾气污染暴露的系统网络优化模型

谭 宇，严余松，孙湛博，户佐安，姚志洪

(1.西南交通大学a.交通运输与物流学院，b.综合交通大数据应用技术国家工程实验室，成都611756；2.成都工业学院，成都611730)

0 引言

近年来，我国空气污染问题日益突出，严重影响了城市居民的身体健康和生活质量，研究表明长时间暴露于污染的空气中会对身体健康造成长期或者短期的影响[1].且空气污染中机动车尾气污染高达70%，作为城市空气污染的主要来源之一，其含有CO、NOx和PMx等多种有害气体.因此如何有效地治理车辆尾气排放已成为绿色交通领域里一个重要的研究议题.

目前我国控制尾气污染的主要方法是限制车辆的排放水平[2]，但是没有限制车辆的行驶里程，这导致车辆尾气的排放总量没有得到有效地控制.且传统的交通规划并没有考虑如何减少车辆尾气的排放量，因此，现代城市交通发展与尾气污染治理之间的矛盾引起了国内外众多学者的广泛关注.Yin等[3]采用定价的方法，将车辆尾气排放产生的外部效应内在化，并指出合理的定价方案可以使路网中的车辆行驶时间和排放率达到相对最优的状态.Sharm等[4]基于传统的交通分配模型，将出行时间和交通排放作为共同的目标进行优化，发现出行时间与交通排放之间存在均衡关系.

机动车尾气对空气的污染分为两个阶段：第1阶段是污染物从源头产生，第2阶段是污染物扩散到周围的空气中.针对第1阶段学者们提出了CMEM，VT-MICRO，MOVES等众多尾气排放估算模型，但受模型输入参数，数据可获取性的限制，基于实际案例构建排放预测模型逐渐成为主流.如胥耀方等[5-6]分别从路段和交叉口的角度，运用北京市的实测数据，建立了排放测试模型，研究发现该排放测试模型的计算精度高于MOVES模型.宋国华等[7]利用机动车比功率(VSP)来刻画交通排放，并通过实际交通数据验证了该模型在实现油耗与排放实时量化评价上的优势.针对第2阶段，现有描述车辆尾气扩散的模型主要包括高斯烟羽模型、箱体模型、拉格朗日模型等，其中高斯烟羽模型因其简单明了的结构被交通领域的研究者广泛应用[8-9].

显然，大量的研究主要集中在3个方面：①结合交通模型，通过优化交通组织减少道路中车辆的尾气排放；②根据交通特性，建立排放估算模型；③运用扩散模型，描述车辆尾气的扩散过程.这些文献主要是以车辆为研究对象，鲜有文献考虑到车辆尾气对出行者的影响，即尾气污染暴露.

因此，本文创新的以出行者为研究对象，建立了考虑尾气污染暴露的系统网络优化模型.该模型主要包括两个部分：第1部分为车辆尾气排放估算模型，其作用是估算路段上的车辆尾气排放量；第2部分为排放浓度估计模型，它结合高斯烟羽模型，以车辆尾气估算模型所得的尾气排放量作为输入，描述路网中车辆尾气的扩散过程，从而获得近地面的车辆尾气排放浓度.所获得的尾气排放浓度与出行者在该路段上停留时间的乘积，即为出行者的尾气污染暴露.

本文从交通管理者的角度出发，基于传统的系统网络优化模型(SO-TT)，建立考虑尾气污染暴露的系统网络优化模型，为建立绿色宜居城市提供一种合理的路网交通流优化模型，也为交通管理部门提供一种新型的绿色交通规划思路.

1 模型的建立

1.1 车辆尾气排放估算模型

车辆尾气中含有CO、NOx和PMx等众多对人体有害的气体.其中温室气体获得了人们更多的关注，但是Alexopoulos等[10]认为CO含量是描述车辆尾气对大气污染程度的重要指标，因为：①空气中CO几乎全部来自车辆尾气；②CO是尾气中最为危险的一种有害气体；③其他气体的预测模型与CO的预测模型类似.为了简化对研究问题的描述，本文仅选择CO作为代表污染物进行研究.参考文献[4]给出了基于路段的车辆尾气排放率估算模型如式(1)所示，式(2)为美国BPR函数.

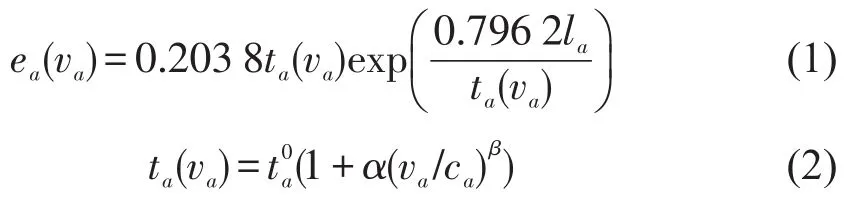
式中：a为路段，a∈A，A为路网中所有路段的集合；ea(va)为路段a上的排放率(g/(veh⋅h))；va为路段a上的流量(veh/h)；la为路段长度(km)；ta(va)为路段行驶时间(min)；为自由流行驶时间；ca为路段通行能力；α β为模型参数，一般取值为0.15/4.

1.2 尾气排放浓度估计模型

本文假设路段上的车辆不存在差异性，所有车辆的排放强度是相同的，每一辆车即为一个排放源，排出的尾气按照一定的运动方式扩散到空气中.为了描述点源扩散到周围空气中的过程，1994年Turner[11]提出一种计算连续平均点源的扩散模型，即高斯烟羽模型，如式(3)所示，其原理如图1所示.

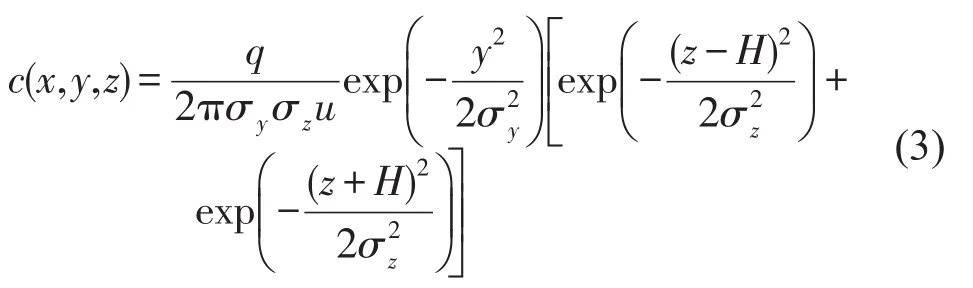
式中：c(x,y,z)为在接收点(x,y,z)处的污染物浓度(mg/m3)；x为污染源排放点沿着风向上任意一点的距离(m)；y为扩散中心轴在直角水平方向上任意一点的距离(m)；z为从地表到任意一点的高度(m)；q为排放率(g/s)；u为平均风速(m/s)；H为排放源离地面的高度；σy为垂直于风向的尾气浓度分布的标准差(m)；σz为竖直方向尾气浓度分布的标准差(m).其中σy与σz的大小与大气稳定度和x的距离有关.根据文献[12]，城市区域的大气稳定度的等级为D，相应的σy与σz的计算方法，如式(4)和式(5)所示.

图1 高斯烟羽模型[12]Fig.1 Gaussian dispersion model[12]

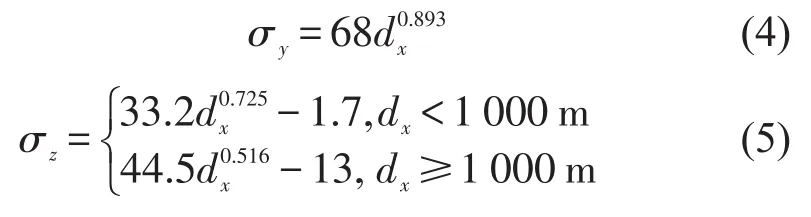
式中：dx为顺风方向检测器离x轴的距离.

本文考虑近地面的尾气排放浓度，所以假设Z=0，H=0，可将式(3)简化为式(6)，x≥0表示接收点在顺风方向，x＜0表示接收点在逆风方向.

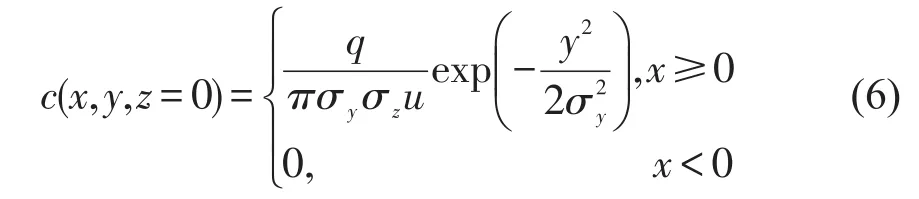
为了计算整条路段的车辆尾气排放浓度，本文采用文献[13]提出的方法，将点源(1辆汽车的尾气排放强度)拓展至线源.该方法将1条路段平均分为若干小段，每一小段作为1个等效有限线源(FLS)e，且每一小段的中心即为e的中心，所以每一个e对尾气排放浓度的影响Ce(x,y)可表示为

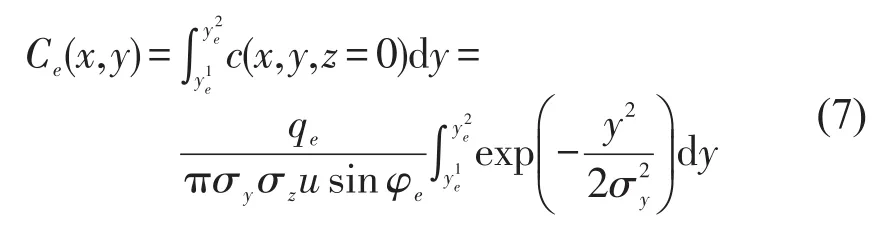
式中：φe为等效有限线源e与风向之间的夹角，为接收点离等效有限线源e起始两端的距离.

需要注意的是本文存在2个坐标系，第1个坐标系是全局坐标系，即路网的实际坐标；第2个坐标系为局部坐标系，即相对坐标.本文在计算接收点(x,y)处的尾气排放浓度时所采用的坐标系即为局部坐标系，全局坐标与局部坐标之间的转换关系由式(8)和式(9)计算可得.坐标变换的原理是：在全局坐标系下，以路网中每个等效有限源e的中点(Xe,Ye)为原点(0,0)，以顺风方向为x轴，垂直于风向为y轴建立局部坐标系，然后将全局坐标系下路网中的接收点(X,Y)转换到局部坐标系下，其中θ为风向(逆时针方向为正)与全局坐标X轴之间的夹角.

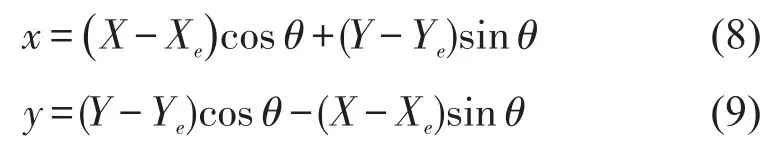
1.3 基于CO污染暴露的系统网络优化模型

车辆尾气对出行者的影响不仅与尾气浓度有关，也与停留在尾气中的时间长度有关.所以，本文的目标函数同时考虑了车辆尾气排放浓度与出行者在车辆尾气中停留的时间，来描述出行者在车辆尾气中的暴露程度，即路段上出行者的尾气污染暴露等于路网中总的尾气排放浓度与在该路段上停留时间的乘积.本文建立的考虑CO污染暴露的系统网络优化模型(SO-CO)，如式(10)所示.

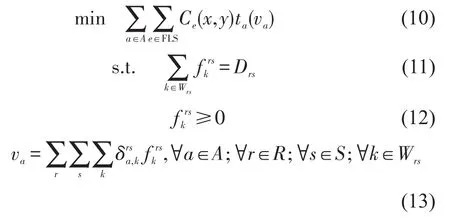
式中：R为路网中出发地的集合，r∈R；S为路网中目的地的集合，s∈S；Wrs为出发地r和目的地s之间的所有路径集合；Drs为出发地r和目的地s之间的OD交通量；为出发地为r目的地为s的OD间的第k条路径上的流量；为0-1变量.

本文采用传统系统网络优化模型的约束条件，如式(11)～式(13)所示.其中式(11)为交通流守恒条件，即OD对之间各条路径上的交通量等于OD对之间的交通总需求；式(12)表明OD对之间各条路径之间的流量不小于0；式(13)代表路段上的流量等于途径该条路段的所有OD对之间的路径流量的叠加.

2 求解算法

本文所建立的模型是1个非线性有约束的最优化问题，且目标函数与路段流量之间的关系并不独立，即出行者的尾气污染暴露不仅与本条路段的车辆尾气排放浓度有关，还与路网上其他路段的尾气排放浓度有关.所以传统的连续平均法(MSA)、对角化算法等并不适用.因此本文运用AMPL语言对模型进行编译，通过一种能够高效地求解非线性优化问题的求解器MINOS对模型进行求解.运用Matlab计算在特定风向下经过坐标变换后的模型参数和变量.模型的求解算法步骤如图2所示.

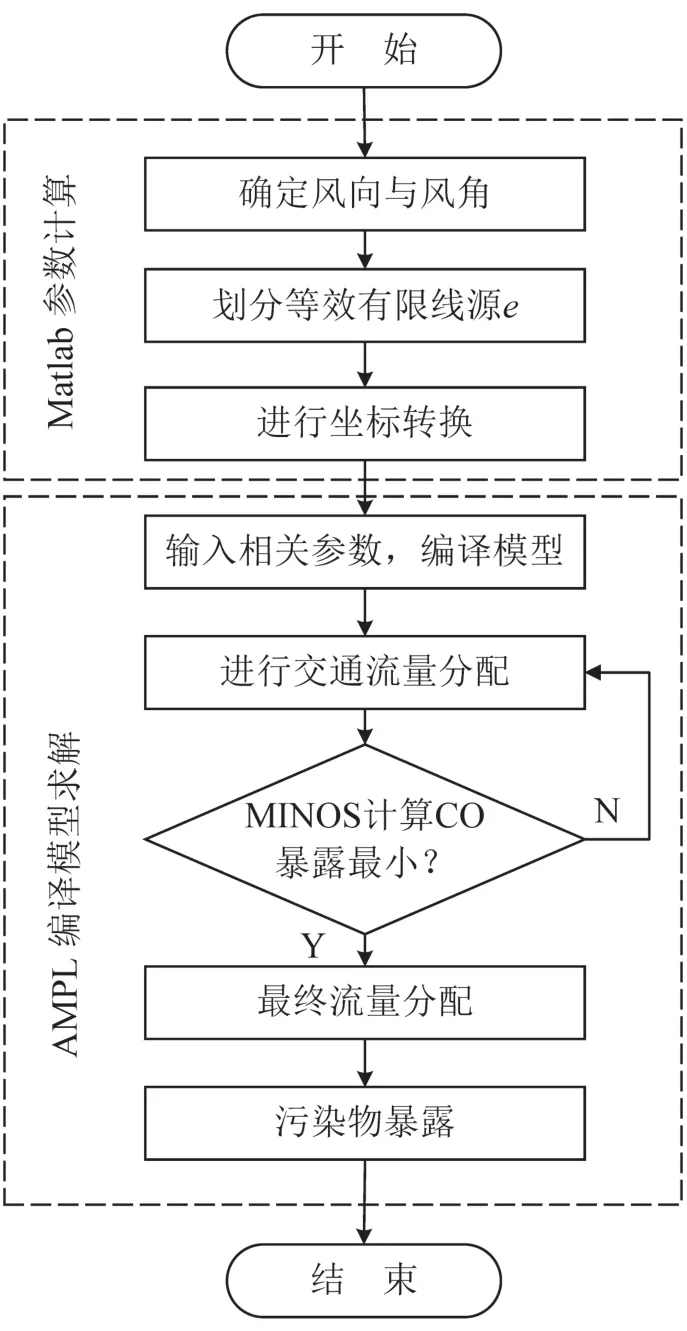
图2 算法框架图Fig.2 Illustration of the algorithm

3 算例分析

3.1 参数设定

本文运用经典的Nguyen-Dupuis网络[14]进行算例分析，如图3所示，各路段的具体参数如表1所示，其中路段长度是根据文献[14]的自由流速度，以速度48 km/h计算得到.网络中共有4个OD对：(1,2)，(1,3)，(4,2)，(4,3)，每一个OD对之间的需求量和路径数量如表2所示.

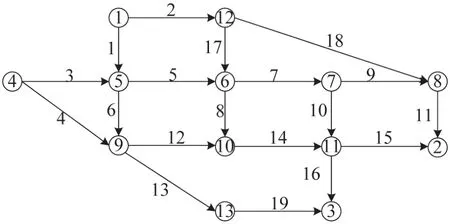
图3 Nguyen-Dupuis网络图Fig.3 Nguyen and Dupuis network

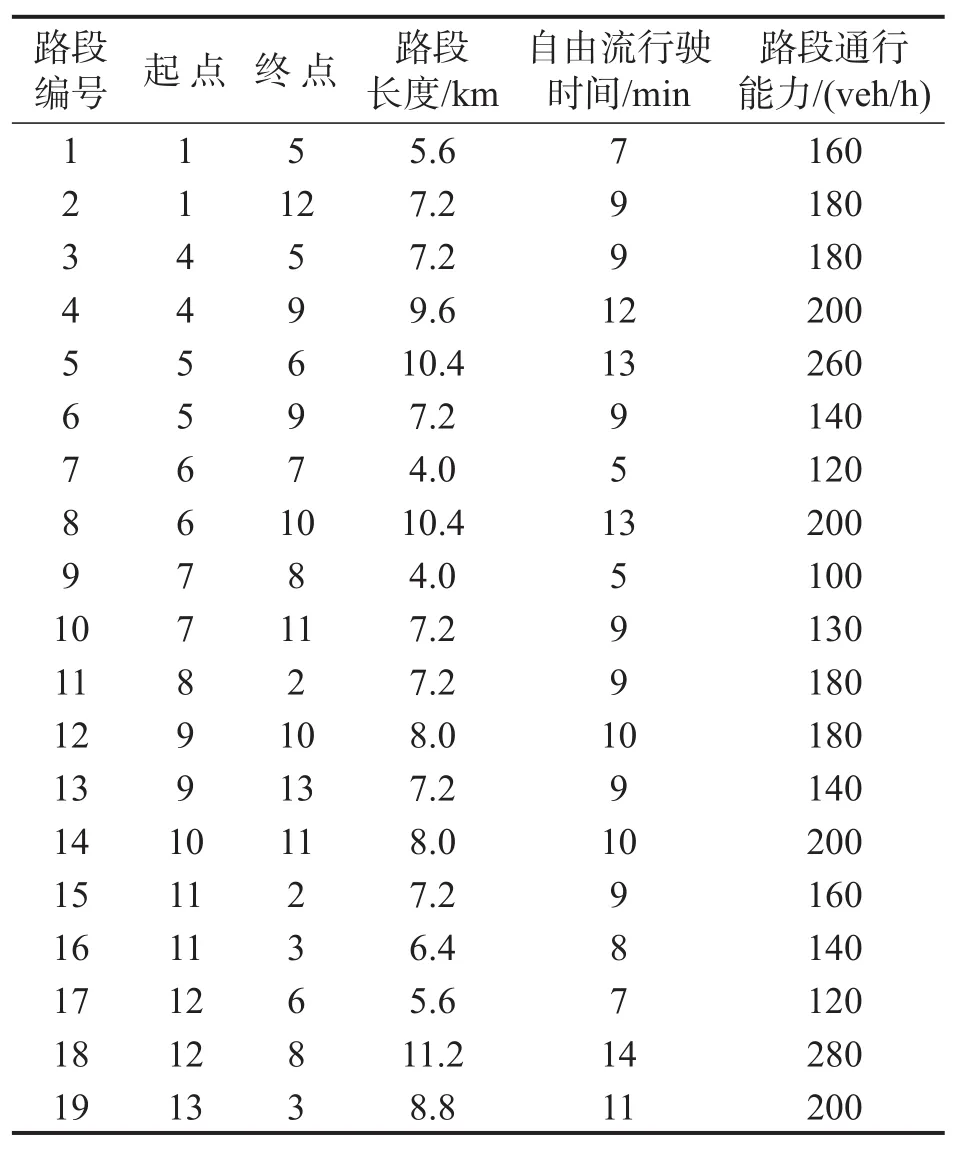
表1 路段参数Table 1 Parameters of links

表2 OD对间的需求量和路径数量Table 2 OD demand and number of paths between each OD pair

3.2 算例结果

本文在风速为0.5 m/s，风向为110°(即东南风)的环境下，假设在每条路段的中点设置一个气体检测器，以每个检测器所检测到的CO浓度作为整个路网在该路段上所产生的排放浓度.分别以路网中的系统行驶时间(SO-TT)和系统CO暴露(SOCO)最低为目的，联合Matlab和MINOS对模型进行求解，计算结果如表3所示.

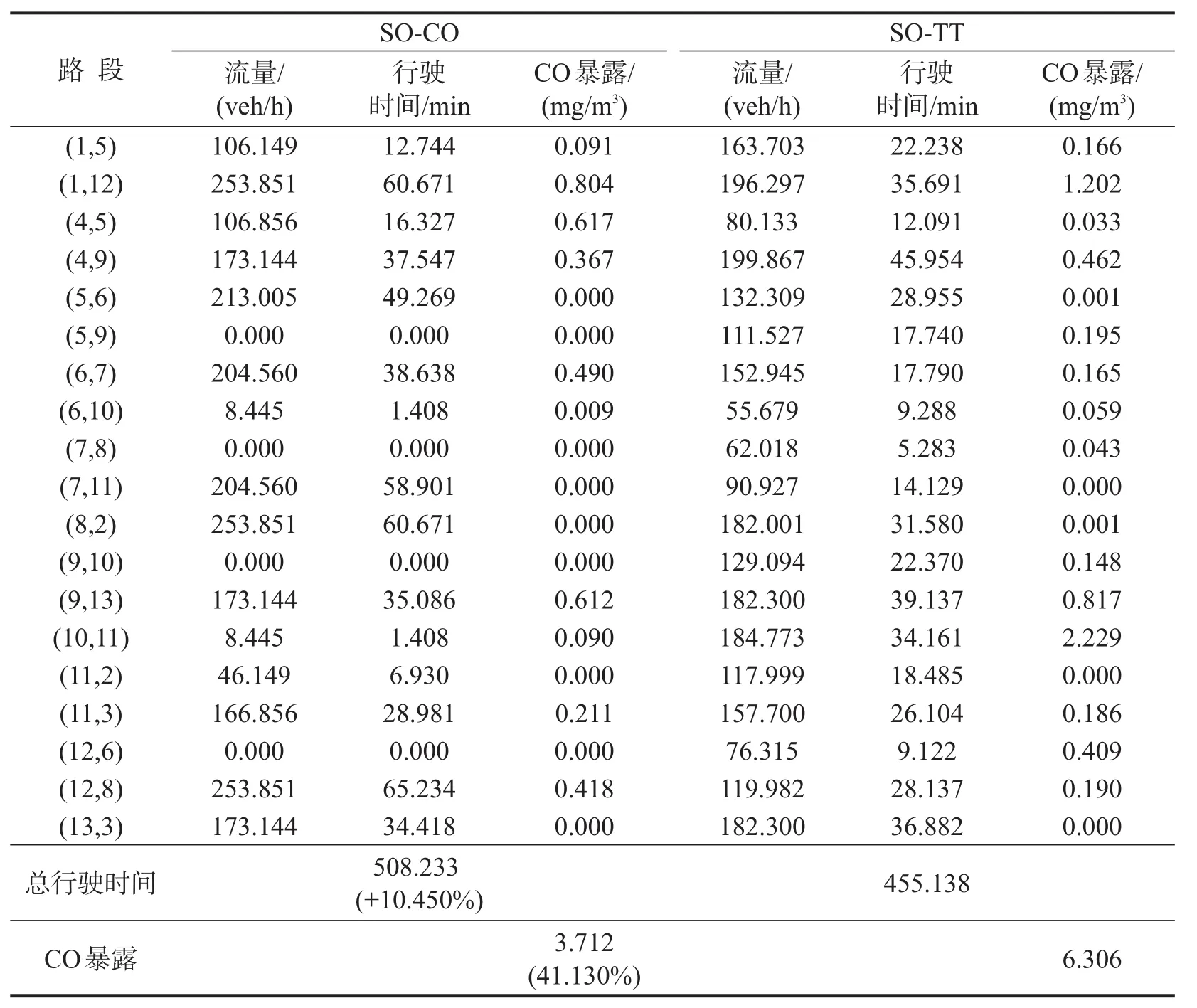
表3 SO-CO与SO-TT计算结果对比Table 3 The comparison of calculation results associate with SO-CO and SO-TT

从表3的计算结果可以看出，当以系统CO暴露最少为目的时(SO-CO)，路网中存在路段流量为0.000的情况，这就说明在规划新的路网时，若以系统CO暴露最少为目标，这些规划路段是不必要的.同时我们也发现有些路段虽有流量通过，但该路段上的CO暴露为0.000，例如路段(13,3)，出现这种现象的原因是算例设计的风向为110°(东南风)，在该风向下路段(13,3)不受其他路段CO排放浓度的影响，且路段上的检测器检测到自身CO排放浓度几乎为0.000，这就导致出行者在该路段上的CO暴露几乎为0.000.这种现象表明，以系统CO暴露最少为规划目的时，不仅需要考虑路网中的流量分配情况，同时也需考虑规划地常年的风速与风向情况.

同时，在SO-CO与SO-TT两种情况下，路网中的流量分配结果不同，得到的系统行驶时间和系统CO暴露也存在明显的差别.

当以系统行驶时间最小为目标时，路网总的行驶时间为455.138 min，总的CO暴露为6.306 mg/m3；当以系统CO暴露最低作为目标时，路网的系统行驶时间为508.233 min，系统CO暴露为3.712 mg/m3.所以，将两个目标下得到的系统行驶时间和系统CO暴露进行比较，不难看出以系统CO暴露为目标时，系统总的行驶时间增加了10.450%，而CO暴露却减少了41.130%，系统CO暴露的降低幅度大于总的行驶时间增加的幅度，这说明本文所建立的模型能够以牺牲系统小部分行驶时间为代价，有效地降低路网中的尾气污染暴露.

3.3 模型对比分析

为了更好地探究系统行驶时间与系统CO污染暴露之间的关系，本文建立了一个双目标模型，如式(14)所示.

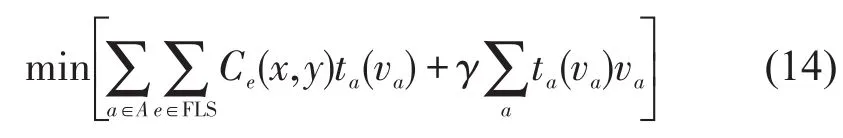
模型的第1部分为CO污染暴露，第2部分是行驶时间，γ是两个目标函数的价值系数，即对两个目标之间的权衡，该模型同样遵循式(11)～式(13)的约束.该双目标模型的计算结果如图4所示.

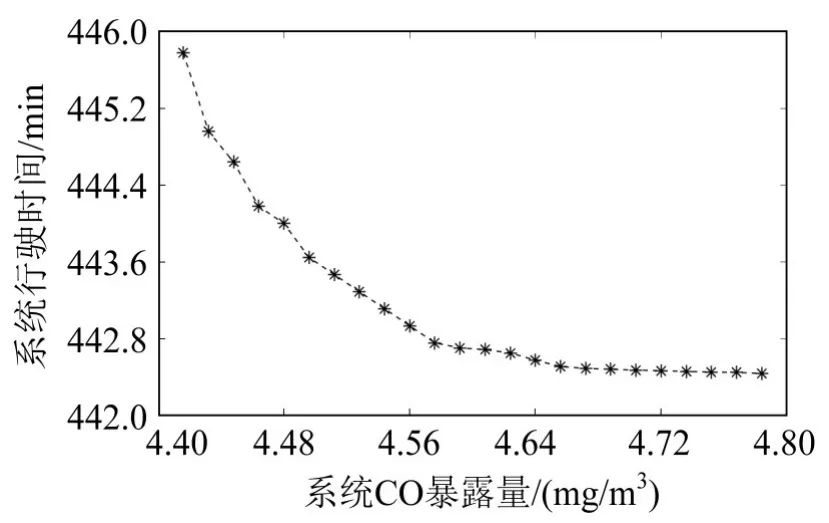
图4 系统行驶时间与系统CO暴露之间的关系Fig.4 The relationship between total travel time and total emission exposure

图4的计算结果表明，本文提出的双目标模型不能同时使系统总的行驶时间和系统总的CO暴露达到最优，但是两者之间存在Pareto优化.图4中曲线上任意一点的斜率代表了两者之间的权衡关系.所以，当交通管理者同时以系统总时间最小和系统总的CO暴露最少为目的进行路网规划时，该结果可以作为权衡行驶时间与尾气污染暴露的重要参考依据.

4 结 论

本文基于传统的系统网络优化模型，结合高斯烟羽模型，从时间和空间上，创新地构建了考虑尾气污染暴露的系统网络优化模型，通过算例分析，可得出以下结论：

(1)与传统的系统网络优化模型相比，本文所建立的考虑尾气污染暴露的网络优化模型能够以牺牲系统小部分行驶时间为代价(+10.450%)，有效地降低路网中的尾气污染暴露(-41.130%).

(2)系统总的行驶时间与系统总的尾气污染暴露之间的关系呈现Pareto优化，该成果可为交通管理者进行路网规划时，如何权衡时间与尾气污染暴露的关系提供相关的理论基础与参考依据.

因此，本文为交通规划与管理部门提供了一种全新的绿色交通网络规划思路，对于降低路网尾气污染暴露具有一定的优势，但是本文忽略了路网中各种车辆的不同交通特性与道路特性，所建模型仅适用于宏观层面的规划.未来可在本文基础上考虑路网中车辆的不同特性和道路特性，分析在不同的风速与风向条件下路网中尾气排放浓度的变化情况，使新的模型应用范围更广，同时可运用实际检测数据对模型进行修订，使模型能够为我国交管部门提供更加准确的理论依据.