SPA和DS证据理论的多传感器航迹关联方法*
2018-12-28杨军佳叶晨亮刘志青廉博
杨军佳,叶晨亮,刘志青,廉博
(陆军炮兵防空兵学院 郑州校区,河南 郑州 450000)
0 引言
现代战争中,为了获取某一区域比较完整且准确的战场态势信息,往往部署多个可以覆盖该区域的传感器,如何判断来自于不同传感器的航迹信息代表同一个目标显得尤为重要。目标航迹关联的目的就是从多个传感器获取到的比较完整的态势信息当中,判定某些航迹源于同一目标,从而在保证态势信息完整的同时,减少冗余信息,提高信息的准确性。目前航迹关联主要有基于统计和基于模糊数学的2种方法,如最大似然概率法[1]、综合相似接近度[2]、模糊门限法[3-13]等等。这些关联方法具有一定的应用价值,但也存在一些不足:为了达到一定的关联正确率,必须进行大量的仿真以确定最优的门限值等等。本文运用集对分析理论,将同一区域、相同时间不同传感器探测到的目标看成具有一定联系的不同集合,从相同、差异和对立3个方面来研究不同航迹点之间的联系,构建不同航迹点之间的贴近度矩阵,通过贴近度矩阵提取最有可能的航迹关联对,利用DS证据理论综合不同因素对航迹关联的影响,以达到解决航迹关联的目的。
1 集对分析理论
联系度表达式为μ=a+bi+cj,其是集对分析理论中2个集合组成的集对在某一问题背景下同异反程度的度量。其中,a,b,c满足归一化条件:a+b+c=1,且a表示2个集合共同具有某些特性的程度,简称同一度;b表示2个集合特性间的差异程度,简称差异度;c表示2个集合在某些特性上正好互为对立的程度,简称对立度。i为差异度标记或相应系数,可视不同情况取值[-1,1],通常取值为1;j为对立度标记或相应系数,规定取值为-1。
集对贴近度是指,当集对联系度中b≠1时,同一度a在同一度与对立度c之和中所占的比重。从上述描述中,可以得出集对贴近度的表达式为
g=a/(a+c).
(1)
从式(1)中可以看出集对贴近度表示2个集合之间的贴近程度,且g∈[0,1]。g→1,表示2个集合越接近。
2 SPA和DS证据理论的航迹关联方法
文献[14]中已将集对分析中常见的对立概念分为有无型、倒数型、互补型、正负型和虚实型5种类型,并指出倒数型对立在科技领域中是一种常见而又重要的对立类型。因此,本文以倒数型对立为出发点,进行航迹关联的讨论。
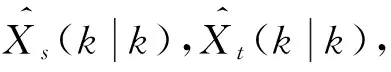
步骤1集对联系数的确立。
(2)
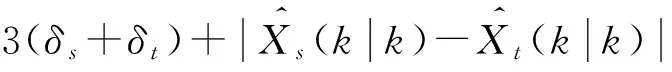
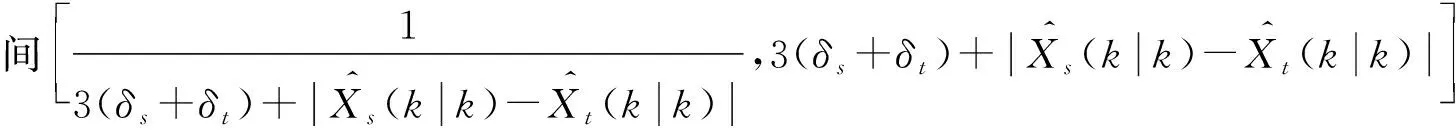
(3)
(4)
(5)
步骤2集对贴近度矩阵的构建
在步骤1的基础之上,由式(1),(3),(4)可以得出在k时刻传感器s探测到的ns个目标与传感器t探测到的nt个目标之间的集对贴近度矩阵为
(6)
步骤3关联判决准则。

步骤4DS证据理论合成规则
在步骤3的基础之上,依据DS证据理论,如果将传感器s和传感器t对目标某一参数状态估计值之间的集对贴近度作为判断目标是否来源于同一目标的证据,则识别框架为Θ={相关,不相关},相关的概率为P(P与传感器之间某一参数状态估计值之间的集对贴近度相关),不相关的概率为1-P。
如果每部传感器能够探测目标的q个参数,则合成DS规则为
3 仿真分析
为便于验证,这里仅以2部传感器探测目标的2个参数为例。仿真环境设置如下:10批目标在传感器探测区域内运动,且其初始位置在x∈(10,20) km,y∈(15,30) km的矩形区域内随机分布,初始速度在100~700 m/s之间随机分布、初始航向在0~2π之间随机分布,2部传感器的位置为(-10,0) km以及(10,0) km,其距离测量误差以及方位测量误差为δdistnce和δangle,且距离测量误差δdistnce在80~300 m之间任意取2个值、方位测量误差δangle在0.5°~2.5°之间任意取2个值,采样间隔均为1 s,仿真时长为50 s,采用蒙特卡罗方法进行100次仿真。
(1) 有效性检验
为检验本文方法的有效性,将本文方法、最近邻方法以及文献[2]方法用于对10批目标进行航迹关联,传感器位置、10批目标航迹及不同方法对目标的正确关联概率曲线如图1~3所示。
图1给出的是2个传感器位置及10批目标的真实航迹,显然仿真环境中含交叉分岔等多种复杂情形。图2给出了采用本文方法以及经典的最邻近法进行航迹关联的正确概率曲线,图3给出了本文方法以及文献[2]方法进行航迹关联的正确概率曲线。其中,图2中最邻近法的门限设置为两传感器对目标测量误差之和的1.5倍,图3中文献[2]的各参数设置为0.5。
从图2与图3中的正确关联概率曲线可以看出:不论是与经典的最近邻方法相比,还是与文献[2]中的方法相比,本文方法的正确关联概率均比较高,证明了本文方法的有效性;同时,本文方法与经典的最近邻方法和文献[2]方法相比,门限设置固定为1/3,不需要为了获得较高的正确关联概率而进行大量的仿真实验以获取最优的门限值,便于工程应用。
(2) 方法复杂性对比
与有效性检验相对应,将本文方法、最近邻方法以及文献[2]方法用于对10批目标进行航迹关联,所需时间消耗如表1所示。
表1给出了3种方法完成10批目标航迹关联所需要的时间。从表中可以看出,本文方法完成关联所需要的时间比最近邻方法要多,但是比文献[2]所需时间要少。主要是本文方法在进行航迹关联的过程中,既有集对贴近度的计算,又有证据组合的运算,导致复杂性比经典的最近邻方法要高;但是,与文献[2]方法相比,完成同样的目标航迹关联所需时间减少了将近40%。

表1 不同方法对10批目标航迹关联耗时统计表
4 结束语
本文研究了多传感器探测目标航迹之间的关联问题,提出了一种基于SPA和DS证据理论的航迹关联方法。该方法将来自不同传感器的航迹点按照集对处理,从相同、差异和对立3个方面进行研究,构建航迹之间的贴近度矩阵,通过寻找集对贴近度的最大值,判断航迹是否来源于同一目标,同时利用DS证据理论将不同目标参数对于航迹关联的支持程度进行合成,以此达到解决航迹关联问题的目的。仿真结果表明,该方法可以用于多传感器探测航迹之间的关联。
