水下目标识别的规划融合算法*
2018-12-28刘标许腾刘树锋
刘标,许腾,刘树锋
(1.海军指挥学院,江苏 南京 210016;2.海军士官学校,安徽 蚌埠 233012; 3.中国人民解放军94908部队,福建 厦门 361000)
0 引言
水下目标识别是水下作战的重要内容。在复杂海洋环境下,由各种渠道获得的水下目标信息参数,以及由此形成的数据库存在着不完整、不确定性,特别是模糊性。而正确有效地进行多传感器数据的融合处理,可以提高水下目标识别系统的自适应性和鲁棒性以及可靠性,同时可以降低信息获取的不确定性等。多传感器数据融合[1-2],是指通过对空间分布的多源信息进行多级多功能处理,得到更高概率、更高精度或置信度的一种数据处理手段或方法,以便为决策者提供辅助。本文结合水下目标识别的特点,提出一种新的规划融合算法,并将其应用到水下目标识别中。
1 水下目标识别融合
水下目标识别不仅受目标本身噪音的影响,还受海水的深度、盐度、温度等因素的影响,因此,水下目标识别具有一定的不确定性,必须由多个传感器识别结果互相印证才能得出较为真实的识别结果。水下目标识别融合,是指根据水下布设的各种传感器输出的初步目标识别判断结果,这些结果可能是不确定的、模糊的,而后经过融合中心算法的处理,得出确定的水下目标识别结果的过程[3]。多传感器数据融合分为像素级融合、特征级融合和决策级融合,本文提出的规划融合算法属于决策级融合,具体融合过程如图1所示。
关于多传感器数据融合系统中的融合算法,比较典型的有D-S(Dempster-Shafer)证据理论及改进算法、神经网络算法、贝叶斯理论、模糊算法等[4-13],这些算法的最大特点就是基于模糊数据的模糊处理,具有很大的不确定性。而本文提出的规划融合算法,通过求最优解,得出最优的目标融合概率值,由不确定性的信息得出了可信的、确定性的融合结果。
2 传感器输出数据形式
在水下目标识别中,多传感器数据融合系统的传感器输出数据,以识别概率值的形式输出。为了对水下目标识别的规划融合算法进行说明,假设在监视区域有G个传感器进行观测,它们可以是相同类型的传感器,也可以是不同类型的传感器。被识别的水下目标,属于由n个已知目标类型所组成的集合,每个传感器根据侦察得到的目标特征参数,进行局部数据处理来估计未知水下目标,然后产生一个传感器输出数据,并送往多传感器数据融合中心。传感器输出数据的形式可表示为
Sg=[mg1:mg2:…:mgn],g=1,2,…,G,
(1)
式中:g为传感器序号;G为系统内传感器的总个数;mg1,mg2,…,mgn表示水下目标识别框架内第g个传感器中n个元素的识别概率值。多传感器数据融合中心,基于从这G个传感器接收到的数据,融合出水下目标的最终识别结果。
3 水下目标识别规划融合算法
3.1 算法依据
规划融合算法是指使用运筹学的方法,建立目标函数和约束条件,通过求解目标函数的最优解,得出水下目标识别结果的一种方法。在水下多传感器目标识别过程中,针对同一个水下目标,各个传感器输出数据的识别概率值mgj(g=1,2,…,G;j=1,2,…,n),均是对应于同一个目标的理想识别值pj(j=1,2,…,n)产生的。由于受环境因素及传感器自身误差的影响,传感器输出数据的识别概率值mgj(g=1,2,…,G;j=1,2,…,n)具有随机性,而且各传感器得输出数据应是相互独立的。因此,在实际应用中,传感器输出数据的识别概率值mgj(g=1,2,…,G;j=1,2,…,n)服从正态分布。规划融合算法,是基于传感器输出数据的识别概率值mgj(g=1,2,…,G;j=1,2,…,n)与理想识别值pj(j=1,2,…,n)之间的差异最小这一思想建立的。通过将各个传感器输出的识别概率值mgj(g=1,2,…,G;j=1,2,…,n)与理想识别值pj(j=1,2,…,n)之间分别建立一个目标函数,而后求解这些目标函数的最小值,则计算结果中的理想识别值pj(j=1,2,…,n),就是最为合理的水下目标识别结果。为度量传感器输出数据中,识别概率值mgj(g=1,2,…,G;j=1,2,…,n)与理想识别值pj(j=1,2,…,n)之间的差别,特建立如下距离函数:
(2)
式中:φ为灵敏度指数,当φ=0.5时,该距离函数即为欧氏距离函数;g为传感器序号;G为系统内传感器的总个数,n为识别框架集合内元素的个数。显然,Tg(p)≥0,只要满足mgj=pj(j=1,2,…,n),则Tg(p)=0。为区别各传感器输出数据的重要程度,可将传感器输出数据的可信度Rg(g=1,2,…,G)进行归一化处理,作为距离函数的权系数,从而可将多目标规划模型转化为单目标规划模型进行求解。
3.2 水下目标识别规划融合模型
根据以上提出的融合思想,建立水下目标识别规划融合模型如下:
(3)
(4)
式中:mgj为在第g个传感器输出数据中第j个元素的识别概率值;pj为识别框架中第j个元素的理想识别值;Rg为第g个传感器输出数据的可信度;φ为灵敏度指数。
经过仿真数据验证,灵敏度指数取值应为:0.5<φ<1,当灵敏度指数φ取0.6时,融合结果具有较高的精度,满足水下目标识别的要求。
水下目标识别规划融合模型,体现了识别概率值mgj(g=1,2,…,G;j=1,2,…,n)和理想识别值pj(j=1,2,…,n)之间的差异。当mgj=pj时,目标函数值为0,当mgj偏离pj时,目标函数值将会增大,通过求目标函数的最优解,便可得出最为理想的识别结果。水下目标识别融合结果的可信度,可根据下式计算得出:
(5)
3.3 模型结果比较
为了更好地比较规划融合算法和以前的各种算法之间的差异,下面列举一组典型的传感器输出数据进行说明,假设水下目标识别框架为U={a1,a2},灵敏度指数φ取0.6,各传感器输出数据的可信度均取1。传感器输出数据如下:
来自传感器1的输出数据:S1=[m11∶m12]=[0.6∶0.4];
来自传感器2的输出数据:S2=[m21∶m22]=[0.6∶0.4];
来自传感器3的输出数据:S3=[m31∶m32]=[0.1∶0.9]。
通过该组输出数据可以看出,尽管a2的均值为0.57,大于a1的均值0.43,但传感器输出数据1,2均支持a1,所以目标是a1较为合理。对该组传感器输出数据,使用Lingo软件编程进行求解,融合结果如表1所示。
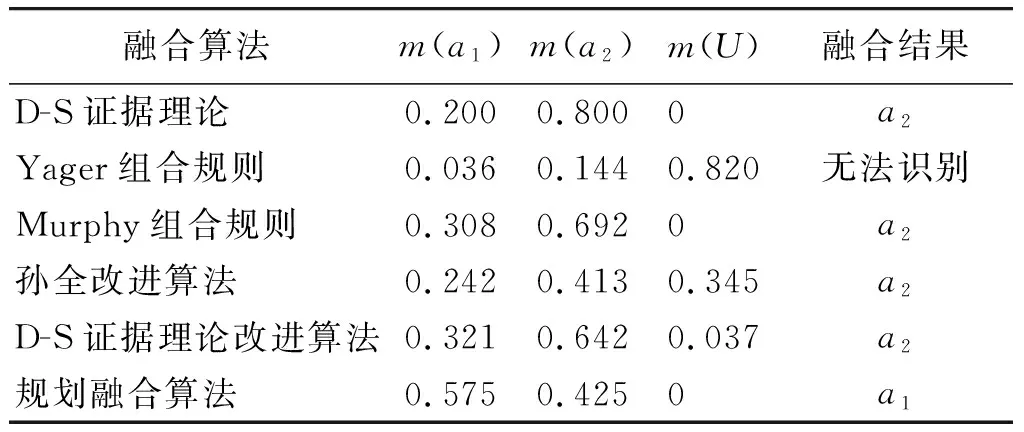
表1 几种融合算法计算结果比较
由表1可以看出,D-S证据理论、孙全改进算法、Murphy组合规则和D-S证据理论改进算法均判定a2为识别目标,融合结果不符合少数传感器判定结果服从多数传感器判定结果这一原则,Yager组合规则则判定目标无法识别,只有规划融合算法给出了正确的融合结果,所以规划融合算法在求解传感器输出数据中有坏值的情况时,优于以前的各种算法。
4 规划融合算法在水下目标识别中的应用
4.1 传感器输出数据
为便于研究,假定在某一海域,由声纳传感器、磁感应传感器、水压传感器等多种传感器,构成水下目标多传感器数据融合系统,进行水下目标识别[14],识别框架为U={a1,a2,a3,a4,a5},其中,a1表示该水下目标是一类舰船,a2表示该水下目标是二类舰船,a3表示该水下目标是三类舰船,a4表示该水下目标是四类舰船,a5表示该水下目标是五类舰船。假设共有4个传感器的输出数据,每个传感器输出数据的可信度分别为R1=0.75,R2=0.84,R3=0.78,R4=0.69,4个传感器的输出数据分别为
S1= [m11∶m12∶m13∶m14]=[0.16∶0.58∶0.03∶
0.15];
S2= [m21∶m22∶m23∶m24]=[0.06∶0.63∶0.14∶
0.16];
S3= [m31∶m32∶m33∶m34]=[0.13∶0.71∶0.06∶
0.08];
S4= [m41∶m42∶m43∶m44]=[0.22∶0.52∶0.07∶
0.14]。
4.2 识别计算
下面将这4个传感器的输出数据代入式(3),并使用Lingo软件编程进行求解,取灵敏度指数φ=0.6,通过计算,得出多传感器数据融合系统的理想识别值pj(j=1,2,…,n)如表2所示。

表2 传感器理想识别值
将4个传感器输出数据的可信度Rg代入式(5),可以得出本次融合结果的可信度为
4.3 目标判定
根据计算出的理想识别值pj(j=1,…,n),可使用最大隶属度原则[15]进行目标判定。依据这一准则,取阈值ε=0.1,计算结果中传感器理想识别值中的最大值p2=max{p1,p2,p3,p4,p5}=0.609 6,而除p2之外的最大值p1为0.140 5,p2-p1=0.469 1>ε。则可判定该水下目标是a2{二类舰船}。
5 结束语
在水下目标识别的多传感器数据融合系统中,融合算法起着至关重要的作用,融合算法的好坏将直接影响着水下目标识别结果的正确与否。本文根据水下目标识别中各个传感器输出数据的识别概率值mgj(g=1,2,…,G;j=1,2,…,n),均是对应于同一个理想识别值pj(j=1,2,…,n)产生的这一融合思想,从目标函数出发,建立了基于距离函数的规划融合算法,通过求解规划融合模型的最优解,得出了最为理想的融合结果。其中,模型中的灵敏度指数给规划融合模型带来了灵活性,可以让使用人员根据具体的海洋环境进行调节,增强了多传感器数据融合系统的灵敏性。仿真结果表明,该算法极大地提高了水下目标识别的准确性和精确度,针对某个传感器输出数据中存在坏值的情况,规划融合算法具有独特的优势。
