请“球”入“盒”问题八例
2018-12-27时英雄
时英雄
(安徽省合肥市第一中学 230000)
学习排列组合问题的时候模型很重要,掌握了一定的模型会在解题中起到事半功倍的效果,不少问题特别是一些人员定岗、名额分配、赠送礼物等实际问题都可以转化为将球放入球盒问题.下面总结几种放球入盒问题模型供大家参考.
模型一 球同,盒同,盒不空
例1 8个相同的球放入3个相同的盒子中,每个盒子中至少有一个. 问有多少种不同的放法?
解析 由于这里球和盒子都相同,每三堆放入3个盒子中只有一种情况,所以只要将8个球分成三堆. 即1-1-6、1-2-5、1-3-4、2-2-4、2-3-3五种,故将8个相同的球放入3个相同的盒子中,每个盒子至少有一个, 有5种不同的放法.
结论一n个相同的球放入m个相同的盒子(n≥m),不能有空盒时的放法种数等于n分解为m个数的和的种数.
模型二 球同,盒同,盒可空
例2 8个相同的球放入3个相同的盒子中. 问有多少种不同的放法?
解析 与上题不同的是本题中的三堆可以有球数为0的堆,即除了分成上面的五堆外,还可分为0-1-7、0-2-6、0-3-5、0-4-4和0-0-8共五种情况,故8个相同的球放入3个相同的盒子中,有10种不同的放法.
结论二n个相同的球放入m个相同的盒子(n≥m),可以有空盒时的放法种数等于将n分解为m个、(m-1)个、(m-2)个、…、2个、1个数的和的所有种数之和.
模型三 球同,盒不同,盒不空
例3 8个相同的球放入标号为1、2、3的三个盒子中,每个盒子中至少有一个. 问有多少种不同的放法?
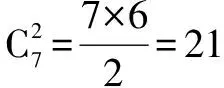
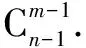
模型四 球同,盒不同,盒可空
例4 8个相同的球放入标号为1、2、3的三个盒子中. 问有多少种不同的放法?
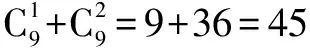
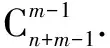
模型五 球不同,盒同,盒不空
例5 8个不同的球放入三个相同的盒子中,每个盒子中至少有一个. 问有多少种不同的放法?
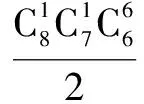
结论五n个不同的球放入m个相同的盒子中(n≥m),不能有空盒的放法种数等于n个不同的球分成m堆的种数.
模型六 球不同,盒同,盒可空
例6 8个不同的球放入三个相同的盒子中,问有多少种不同的放法?
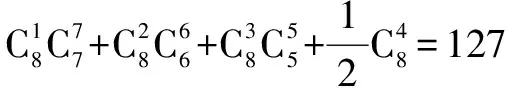
结论六n个不同的球放入m个相同的盒子中(n≥m),可以有空盒的放法种数等于将n个不同的球分成m堆、(m-1)堆、(m-2)堆、…、2堆、1堆的所有种数之和.
模型七 球不同,盒不同,盒不空
例7 8个不同的球放入标号为1、2、3的三个盒子中,每个盒子中至少有一个. 问有多少种不同的放法?
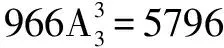
结论七n个不同的球放入m个不同的盒子中,不能有空盒的放法种数等于n个不同的球分成m堆的种数乘以m!
模型八 球不同,盒不同,盒可空
例8 8个不同的球放入标号为1、2、3的三个盒子中,问有多少种不同的放法?
结论八n个不同的球放入m个不同的盒子中(n≥m),可以有空盒的放法种数等于mn种.
