基于CVaR准则的共享单车区域投放策略研究

张 璇 邵晓峰

（上海交通大学 安泰经济与管理学院，上海 200030）

1 问题背景与文献综述

近两年，以摩拜和ofo为首的共享单车在我国主要大城市逐渐兴起，并对人们的日常出行造成了巨大的影响。实际上，共享单车源于1965年荷兰的“白色自行车计划”，这被视为市政共享单车的开始。2010—2014年，国内外逐渐有一些企业参与城市共享单车的运营，通过承包机制来进行有桩共享单车的运营。截至2016年，全球有超过1000个共享单车运营机构和300个在建运营商。而在2017年，共享单车迎来爆发的一年，实际的共享单车运营商远大于这个值。由于国外的共享单车一般是有桩单车，与摩拜和ofo等无桩共享单车相比，有桩单车需要一个固定的停车站点，在这个停车站点中有固定的桩位用于停放自行车。人们在使用的时候，需要先到停车站点取用一辆车，然后骑行到自己目的地相近的另一个停车站点。无论是人们在取用还是在停放自行车时，由于停车站点的桩位决定了该站点的车辆最大停放量，所以无论是取用车辆时发现站点中的车辆已经被别人取用完毕，还是停放车辆时发现没有桩位可以停靠，桩位的数量都在显著影响人们的使用体验。因此，一部分学者开始研究停车站点的位置选择以覆盖更大的区域，或者是满足消费者使用的停车站点的桩位数量以及库存数量等。但更多的学术研究针对另一个问题。由于共享单车的需求集中（时间集中于上下班、地点集中于公司-地铁-住宅），共享单车运营企业需要用一辆有容量限制的载货汽车在不同停车站点之间进行车辆调控，使得每个站点的库存量等于其需求量。由于所有共享单车都停留在车站中，那这样的一个问题将是一个更加复杂的旅行商问题（TSP problem：travelling salesman problem）。学术界许多研究都在试图寻找更加优化的方法去解决共享单车的跨区域优化问题。J Schuijbroek等给出了在一定服务水平要求下共享单车系统优化模型，并且用MIP等不同的启发式算法进行了求解，其贡献主要在于算法。M.Benchimol等将共享单车优化问题与交换问题相互借鉴，在调节车辆不同容量下给出系统的最优化调节路径。Daniel Chemlaa等将之前不必要的约束去除，使得每一个停车站点都可以多次到达，并且在此期间，即使是需求没有满足的站点，调节车辆依然可以从中调用共享单车到其他站点，这使得每个站点都可以起到一个缓冲的作用，学者将其称为SVOCPDP问题（a Single Vehicle One-commodity Capacitated Pickup and Delivery Problem）。

由于在此之前，国内外的共享单车一般都是有桩单车，有桩单车与摩拜、ofo类的无桩单车有着许多相同和不同点，这也是我们本次研究的出发点之一。它们的相同点在于，由于消费者使用单车的核心需求相同，基本都是解决“最后一公里”问题，所以有桩单车和无桩单车的需求都相对集中。也就是说，单车使用在时间上集中于人们的上下班时间，在空间上集中于地铁站等公共交通枢纽。国内一家咨询公司的研究表明，目前共享单车用户的出行中，有68%是使用共享单车去地铁站或者公交车站，仅32%是直接前往目的地。这使得我们对于无桩共享单车的研究可以与有桩共享单车一样，主要分析地铁站或者公交车站的需求满足情况。由于某一地铁站的人员流通量和需求量又远大于某一公交车站的需求量，我们本次研究的重点也将集中于分析某一地铁站的库存水平，即在每天清晨地铁站的共享单车车辆数处于各种水平下，面对已知概率密度分布的需求，共享单车运营企业的效益可以达到最高。

无桩单车与有桩单车的不同点，也是本次研究重点关注的。我们认为，无桩单车与有桩单车使用方式上的不同，导致了需求产生方式上的差异。无桩单车不需要固定的停车站点，也就是说人们在使用共享单车时不需要专门走到一个停车站点，而专门走到一个停车站点意味着共享单车用户是自发、主动地使用共享单车，而不是被停车站点的车辆（库存量）诱发的。由于这种需求是自发的，并且是先于用户到达停车站点之前的，所以它与停车站点的库存量是无关的。也就是说，停车站点的库存量只会影响到需求被实际满足的情况，但不会影响到需求本身。而无桩单车由于不需要固定的停车站点，它可以比较自由地分布在地铁站出口周围，并且诱发用户去使用。也就是说，有一部分用户在走出地铁站之前，并没有想到要使用共享单车，但在出站以后，由于看到了周围停靠的共享单车，于是产生了这样的需求。简而言之，无桩单车的库存量影响到用户需求。艾瑞咨询的研究表明，共享单车用户认知的主要途径是通过看到停放／骑行的单车，有许多用户在调查中表示，自己常常是因为看到了周围有共享单车才会使用。

本次基于无桩单车库存影响需求这一核心特点，利用报童模型的变形进行建模。正如上文所述，之前共享单车的研究很少集中在单一区域的单车投放量，并且没有学者利用报童模型去解决这一问题。本文的创新点在于：1）用报童模型解决共享单车单一区域投放量最优化问题；2）提出无桩单车需求产生方式的不同，研究集中在库存影响需求的这一核心特点。

报童模型作为库存管理领域一个非常经典的模型，报童每购进一张报纸的费用为b，售出一份报纸的收益为a，如果报纸剩余，报童可以将剩余的报纸以残值c卖回给生产厂家，面对已知概率密度分布f（x）的需求，报童可以选择某一购买量以最大化他的收益G（x）。许多学者对报童模型进行了扩展，可

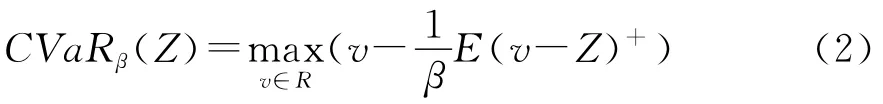
式中，β为置信度，Z是随机变量，E是期望，（v-Z）+代表v-Z与0的较大值。

本文接下来将利用基于CVaR准则的报童模型，以大致分为七类：1）改变或复杂化参数a，比如将需求与售价a建立关系；2）改变参数b，比如将报童的订货量与b建立关系或者将b作为影响所有价格的自变量；3）复杂化c，比如在不同退货政策下有不同的c；4）复杂化f（x），比如需求分布f（x）未知而只知道需求的部分参数等，由于报童模型中对需求分布的假设要求太强，所以弱化对需求的假设成为报童模型延展的重要分支；5）复杂化G（x），在这一分支中最重要的就是引入风险厌恶（risk-aversive）；6）增加其他变量或约束，比如增加报童的预算约束；7）引入多时期或者多产品的报童模型。

风险厌恶被证明是实际存在的，本文采用的报童模型也是这一方面的延展。由于风险厌恶在金融投资中非常重要，所以产生了许多风险衡量方法，最重要的有三种：均值方差、风险估值（VaR：Value at Risk）和条件风险估值（CVaR：Conditional Value at Risk）。Markowitz在1952年提出均值方差，将数理统计的方法应用到投资组合选择中。其经济学意义是，投资者可预先确定一个期望收益，确定投资者在每个投资项目（如股票）上的投资比例（项目资金分配），使其总投资风险最小。但均值方差法对于人们在投资组合中所希望获得的向上（upside）影响和不希望获得的向下（downside）结果的风险厌恶程度相同，这与实际不符。风险估值VaR在1993年被提出，其含义是在一定概率水平（置信度）下，某一金融资产或证券组合价值在未来特定时期内的最大可能损失。用公式表达为

式中，P代表资产价值损失小于可能损失上限的概率，Vp代表投资组合在Vt时间内的损失，Va R代表在给定的置信度β下存在风险的价值，即损失的上限。但VaR法也存在一些局限和缺点，比如不具有风险一致度，不考虑超过VaR的风险等，随后，Rockafe Uar等在2000年提出了CVaR法，其含义是在投资组合的损失超过给定置信度下的VaR时的平均损失值。用公式表达为

CVaRβ=E（-X／-X≥VaRβ）

式中，-X代表投资组合的随机损失，Va Rβ代表在置信度为1-β时的Va R值。

CVaR还有一个更加方便计算的形：考虑不存在和存在缺货损失的情况下，对无桩共享单车库存影响需求的情况进行建模求解，得到某一区域共享单车的最优投放量。同时，分析最优投放量与各个参数之间的关系，并且用数值分析去验证。

2 模型建立与求解

2.1 模型假设与符号

我们研究在某一地铁站口应该投放多少共享单车，可以使得共享单车运营企业在一定效益下面对的效益风险值最低。假设在这样的一个报童模型中，用户使用一辆共享单车（相当于报童卖出一份报纸）的收益为a，共享单车企业投放一辆共享单车的成本为b（相当于报童从生产商那里购入一份报纸的成本），用户没有使用共享单车，但由于投放共享单车给运营企业带来了广告价值等收益为c（相当于报童以残值卖回剩余的报纸），缺货惩罚为s。

共享单车的需求D受到共享单车初始投放量Q的影响，D可以分拆为两个部分，一部分是不受Q影响的部分，即用户在出地铁口前就自发产生的使用共享单车的需求，另一部分是受Q影响的，即用户在出地铁口前并没有考虑使用共享单车，但在行进过程中看到有共享单车而被诱发需求。不受Q影响的需求和有桩共享单车需求相同，用随机变量x表示，其概率密度分布函数为f（x），累计分布函数为F（x）.受到Q影响的那部分需求用αQβ表示，Qβ可以理解为关注度，即用户由于车辆的集中而对单车产生关注，很明显1辆单车停靠在路边和10辆单车停靠在路边所带来的关注度是不同的，α可以理解为这种关注转换为需求的概率。由于αQβ是诱发产生的需求，当不存在库存时就不会产生，所以αQβ的值是小于Q的，即αQβ＜Q。模型假设与符号见表1。

表1 模型假设与符号

2.2 模型建立与计算

2.2.1 不存在缺货惩罚

基于报童模型，在没有缺货惩罚下，对于共享单车运营商来说，有

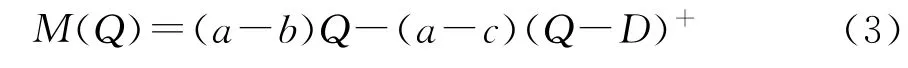
结合式（2），有

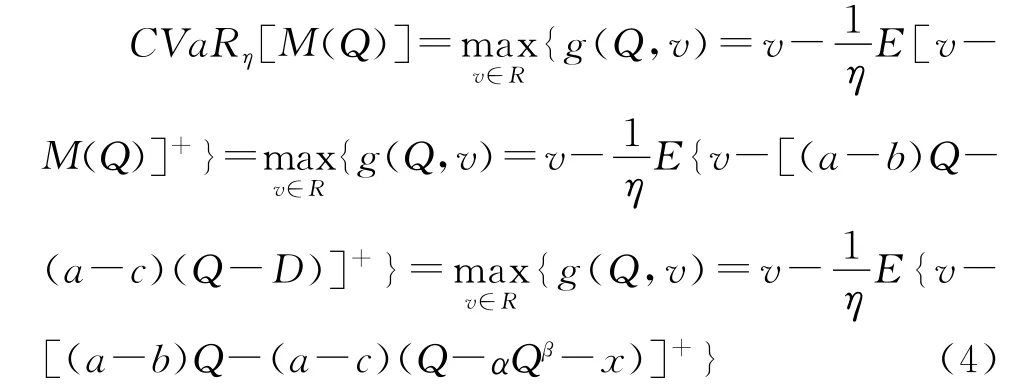
我们的目标是找到Q*，使得g（Q，v）达到最大值。

【结论1】在不存在缺货损失的情况下，假设共享单车的需求量部分依赖于初始投放量，且满足D=αQβ+x，则基于CVaR准则，共享单车运营商的最优投放量Q*满足

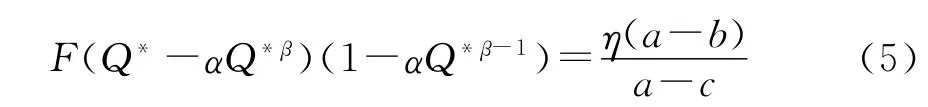
【证明】：

由于存在

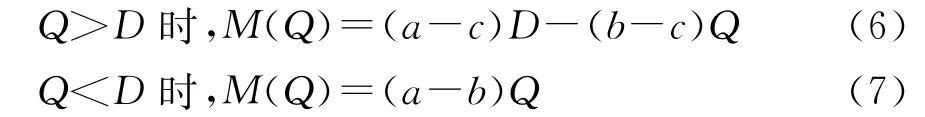
所以有

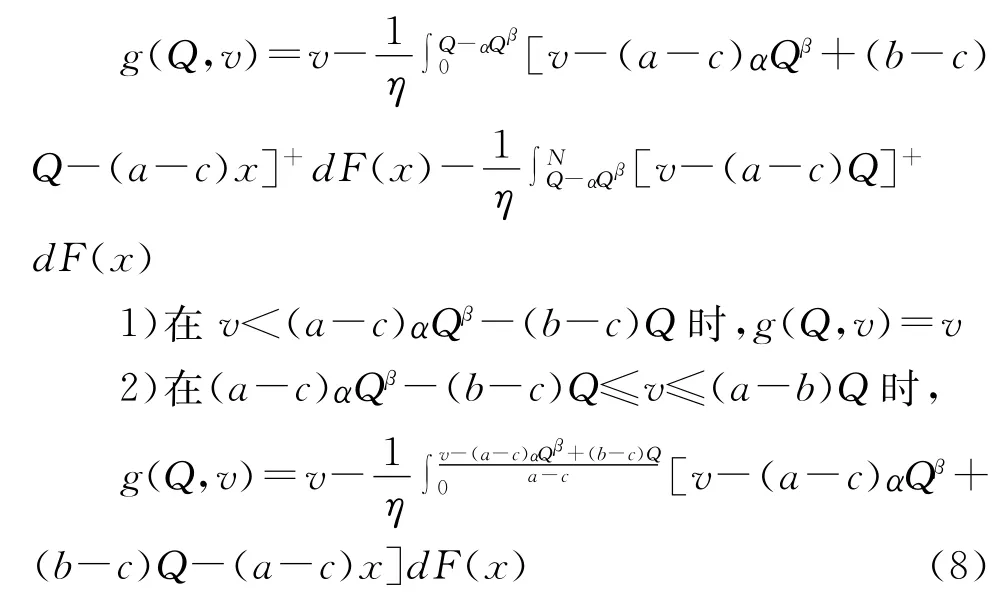
3）在v＞（a-b）Q时，

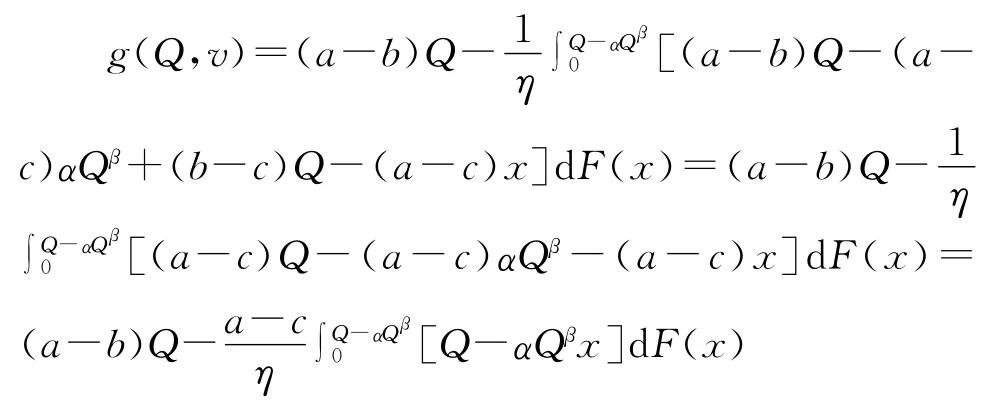
利用分部积分法，最后可以化简得到

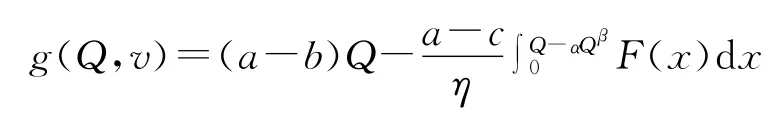
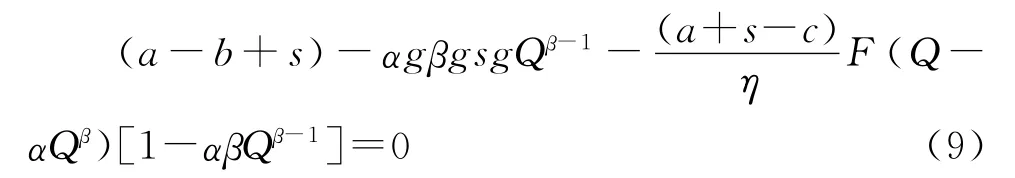
证明：

在存在缺货损失s时，有

D＞Q时，M（Q）=（a-b）Q-（D-Q）s=（a-b+s）Q-sD；

D＜Q时，M（Q）=（a-b）D+（c-b）（Q-D）=（a-c）D+（c-b）D

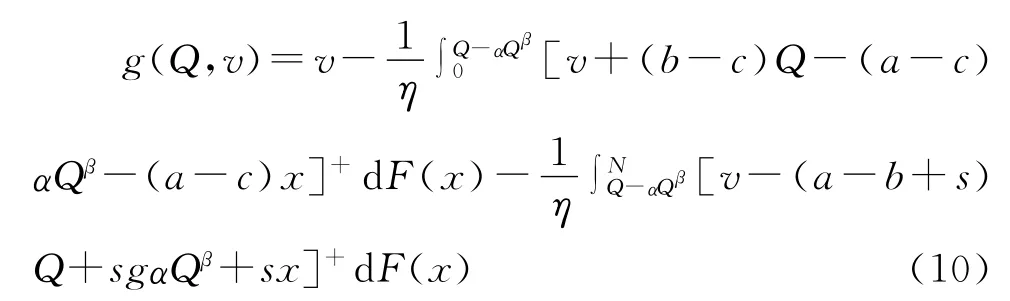
则M（Q）可以表示为（Q-αQβ）［-αβ（β-1）Qβ-2］。很明显，由于α，βη∈（0，1］，a＞b＞c，F（x）＞0，所以二阶导数小于0，所以得到的极值点Q*是极大值点。

综上所述，结论1得证。

2.2.2 存在缺货惩罚时

【结论2】在结论1的基础上，如果考虑了缺货惩罚，即s＞0，假设共享单车的需求量部分依赖于初始投放量，且满足D=αQβ+x，则基于CVaR准则，共享单车运营商的最优投放量Q*满足

同样分三种情况对［a-b］+的格式进行化简，最后可以得到在v=（a-b+s）Q-αsQβ时，g（Q，v）可以取最大值。此时将v=（a-b+s）Q-αsQβ代入式（9），可以得到

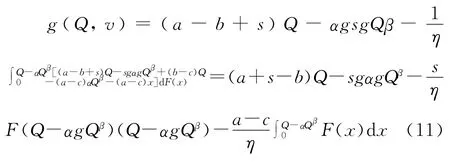
进而得到

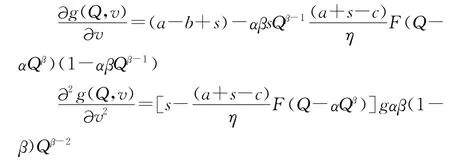
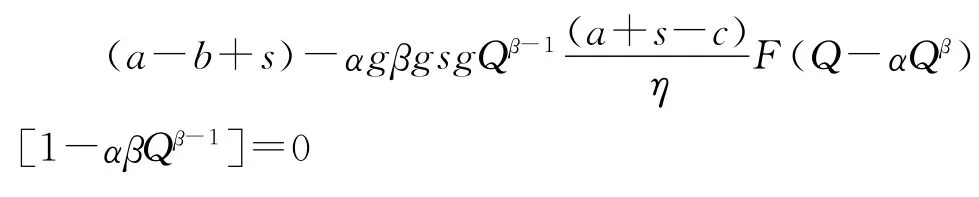
综上，结论2得证。

2.3 参数分析

由于结论1实际上是结论2在s=0下的特殊情况，所以我们对模型的分析基于结论2展开。令

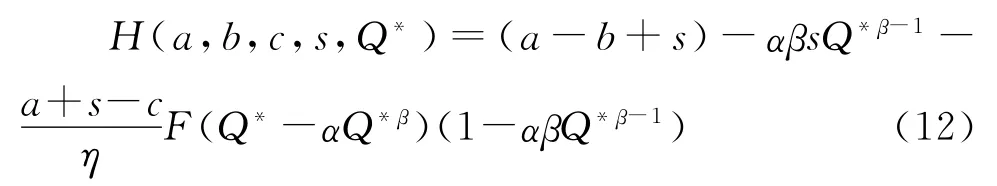
很显然，最优投放量Q*是在H=0时取得的。在2.2部分，我们证明了在Q取得最优值Q*时，g（Q，v）关于Q的二阶导数小于0，即 H（a，b，c，s，Q*）关于Q的一阶倒数小于0，即H与Q负相关。

我们本节分析a、b、c、s四个参数对于收益风险与Q*的变化关系。很明显，我们将 H（a，b，c，s，Q*）对a求一阶导数，得到

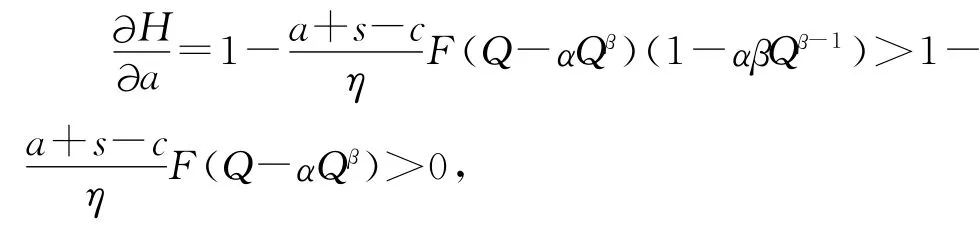
即H与a正相关，由于H与Q负相关，在a增大时，H变大，而H=0时，Q=Q*，所以Q*必须增大，则a与Q*正相关。也就是说，在其他参数不变的情况下，a的增加会引起收益风险性没有实现最小化，此时需要增加一部分投放量才能更大限度降低收益风险。类似分析b、c、s，可以得到b与Q*负相关，结合式（11）可得，在其他变量不变的时候，共享单车运营商单位车辆运营成本的增加，会引起风险收益的减少，但在原有投放量下，风险收益并没有达到最小值，此时需要减少投放量以降低风险。类似地可以得到c、s与Q*正相关，关于a、b、c、s与Q*的相关性，我们在接下来的第三节数值分析与讨论环节，会使用具体的数值进行验证。为减少不必要的计算，我们仅分析s的变化与Q*的关系。

3 数值分析与讨论

在式（9）的基础上，我们进行数值分析，主要想考察模型所得的共享单车最优投放量与参数α、β以及s的关系。由于在模型中有随机变量x的累计分布函数，我们考察模型中的自发需求（也就是随机变量x）满足均匀分布、负指数分布和正态分布时的情况。在实际的模型运用中，需要考察共享单车对应的a、b、c的值，在下面的数值分析中，我们假设a=10，b=5，c=1。

在模型中，我们将需求分为自发需求和诱发需求两个部分，其中诱发需求满足D1=αQβ，这里对α、β寻求现实的解释变量。我们将诱发需求的过程分为两个步骤，首先是获得潜在用户的关注，然后是将这种关注转换为实际需求。在获得关注的这一过程中，我们结合共享单车的实际情况，当潜在用户出现时，很明显路旁的共享单车数量越多，潜在用户越有可能关注到共享单车，同时这种关注度随着车辆数量的增加，其边际效应递减，这样的关注度可以很好地用Qβ来表现。而在关注转换为实际需求的这一过程中，潜在用户在关注到共享单车的存在后，还会考虑其他的一些因素，比如天气、骑行的舒适度、骑行距离等，所以存在转换率α。综合以上，我们可以将诱发需求表示为D1=αQβ。

当随机变量x满足均匀分布时，我们假设其满足［0，100］区间上的均匀分布，可得其期望值为50，方差约为833。在随机变量x满足负指数分布时，我们假设其满足λ=50的负指数分布，可得其期望值为50，方差约为2500。在随机变量x满足正态分布时，我们假设其满足［50，100］区间上的正态分布，可得其期望值为50，方差约为100。

3.1 Q与α和s的关系

考察在β=0.4，η=0.95时，以及不同缺货惩罚s下，最优投放量Q与α的关系，如表2至表4。

表2 均匀分布下最优投放量与α和s的关系

表3 负指数分布下最优投放量与α和s的关系

表4 正态分布下最优投放量与α和s的关系

由表2至表4可以看到，Q与α的取值正相关。结合其现实意义，α越大的时候，即将关注度变为实际需求就越大，诱发效应更加明显，在原有Q的水平下，用于满足自发需求x的库存就越少，此时需要提供更多的库存，即增加Q。同时，我们也发现Q的变动值在α∈［0，1］时并不大，比如在s=0时，α从0.1增加到了1，最优投放量Q的变化值只变动了6.33，最优投放量Q对α的变化并不敏感。此外，在s增大的时候，Q的取值也变大，说明共享单车运营企业如果考虑缺货惩罚，企业需要增加车辆的投放以降低收益风险，即缺货惩罚的增加会增加收益风险，并且s在单位增加时，Q的变动量递减，显示缺货惩罚的增加所引起的风险值边际减少。

3.2 Q与β的关系

考察在α=0.5、η=0.95时，以及不同缺货惩罚s下，最优投放量Q与β的关系，见表5至表7。

由表5至表7可以看到，Q与β的取值正相关，结合其现实意义，β越大，即吸引到的潜在用户量越大，在α一定的情况下，诱发的需求就越大，在原有Q的水平下，用于满足自发需求x的库存就越少，此时需要提供更多的库存，即增加Q。同时，我们也发现Q对β的敏感性还是很高的，尤其是在β大于0.5时，运营企业需要急剧地增加投放量以降低收益风险。

表5 均匀分布下最优投放量与β和s的关系

表6 负指数分布下最优投放量与β和s的关系

表7 正态分布下最优投放量与β和s的关系

4 小结

本文针对我国日益兴起的共享单车进行了研究，发现其无桩的特点最终导致了其需求与有桩共享单车的不同，即库存量（共享单车初始投放量）会影响到其需求量，并基于此假设D=αQβ+x，将共享单车的需求拆分为自发需求x和库存诱发需求αQβ。利用报童模型的变形，在进行建模和模型计算后，给出了作为一个风险厌恶的运营企业，可以使企业在获得某一收益下将风险降至最低的最优区域投放量。同时，在自发需求x满足均匀分布、负指数分布和均匀分布下，考察最优投放量与模型中各项参数的关系，并对各项参数给予了实际情况的解释，从而更好地理解最优投放量与模型中各项参数的关系。