GRACE离散时变重力场的大尺度动态变化模型构建分析

朱传东，刘金钊，王同庆，陈兆辉，张 品，张双喜

中国地震局第一监测中心，天津 300180

地球重力场是地球固有的物理特性之一，它反映了地球内部物质分布、运动及其变化的状态。因此，准确确定地球重力场及其变化历来是大地测量学、地球物理学、海洋学、空间科学以及地球动力学中的重要研究内容，这对于深入研究地球形状与内部构造、防震减灾、勘查矿产资源、保障国防安全等诸多领域具有非常重要的意义。

地球重力场时刻随着地球质量的重新再分布而变化。由于难以获取瞬时的地球重力场模型，人们通常采用一段时期内的观测数据求取其平均地球重力场模型。如果观测时间足够短，则可将解算的模型看作反映该段时间重力场变化的“时变重力场模型”。重力恢复与气候实验卫星GRACE(gravity recovery and climate experiment)自2002年发射以来，已累积获取了近15年的时变重力场模型序列，这些数据一般按月或周发布，并以离散的引力位球谐系数(Clm,Slm)表达，以代表观测期间全球重力场的平均变化[1]。但事实上，地球重力场是随时间连续变化的，为更好描述其动态变化过程，就需为离散的球谐系数构建函数模型，即在传统的描述三维空间变化的重力场模型基础上引入时间变量，以构造出能同时描述重力场时空变化的四维结构模型(图1)，这能为各种时变重力场参量特征分析及其应用研究提供有意义的基础参考。

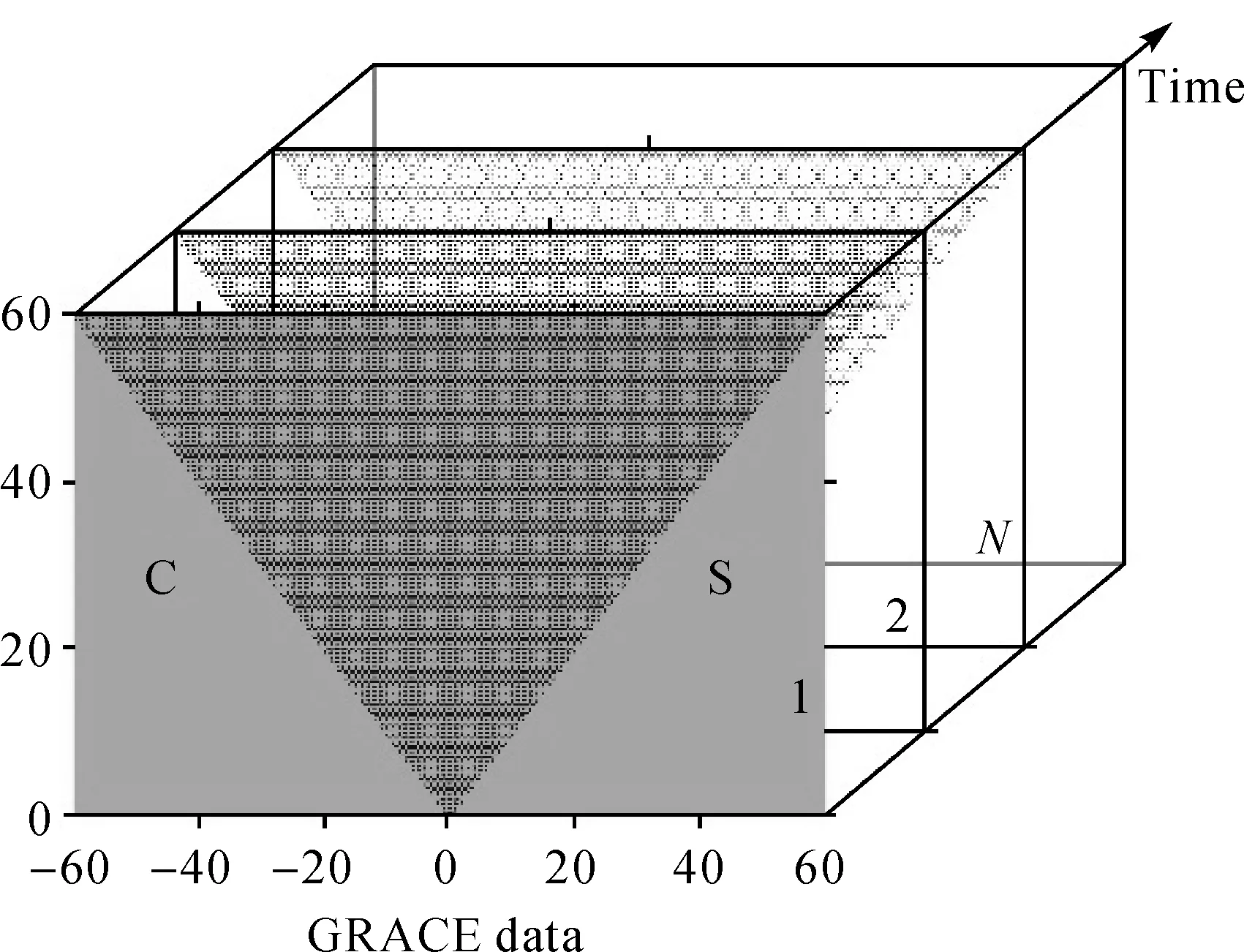
图1 GRACE时变重力场模型Fig.1 GRACE time variable gravity model

现有的GRACE时变重力场在其动态变化模型的提取及构建过程中仍面临两个主要问题。一方面，受仪器测量误差、相关误差、截断误差和混频误差等影响，GRACE解算结果的中高阶球谐系数会存在较大误差。目前，联合以高斯滤波为代表的滤波因子和去相关滤波方法虽然可有效去除部分误差，但不同滤波方法的参数选取不同，则时变重力场模型的中短波部分的改正量也会有所不同，其相应的滤波效果(信噪比)也会有所差异[2-6]。另一方面，在年际、季节性或更短的时间尺度上，时变重力场变化主要产生于地球表面圈层的水循环、大气及海洋质量变化等[7]。因此，多种时空尺度地球物理场过程的相互复杂作用，本质上决定了时变重力场的非线性变化特征。例如，以往的研究结果表明，基于不同时间跨度的GRACE数据反演的极地冰盖物质平衡在整体和局部上呈现出显著的年际变化特征，可导致不同时间段的冰雪质量变化趋势存在显著差异[8]。即使在全球范围内，GRACE反演的陆地水质量变化也存在显著的加速度信号，这会对趋势信号的评估造成较大干扰[9-10]。在此背景下，仅顾及趋势项和季节项的影响且以时间序列必须线性演变或谐波型周期变化为前提的假设方法，就很难准确描述时变重力场的非线性动态变化过程[11-12]。

目前，以经验正交函数分解(EOF)及其扩展形式多通道奇异谱分析(MSSA)为代表的统计分析方法，是构建GRACE离散时变重力场动态变化模型的有效技术手段[13-14]。其中，EOF又称为主成分分析，在以往的研究中，可在频谱域和空间域上应用于GRACE矩阵数据的数据压缩降维、噪声消除[15-16]，以及主要地球物理场模态的提取分析解释[17-19]。不过，EOF在将GRACE矩阵数据变换为统计不相关的新变量过程中会存在模态混叠问题，由此不能准确解释各分量的真实物理意义[14,20]。有别于EOF方法，MSSA可进一步利用迟后协方差矩阵，通过迟后排列的空间型表达原场中主要空间结构的时间演变特征。对于事先未知物理本质的系统，MSSA尤其不需要假定时间序列必须线性演变或谐波型周期变化，而是根据资料本身最优确定的，从而识别原序列的倾向、周期和噪声信号[21]。有鉴于此，MSSA特别适用于提取GRACE矩阵数据的非线性变化特征[11,22]，尤其是在局部空间域上分析、解释与多种气候模态相关的GRACE陆地水文变化过程[23-24]。不过，MSSA直接应用于GRACE月球谐系数矩阵的信号提取过程中会受到系统相关误差和计算效率的显著影响，由此不能有效识别其准确的物理变化特征[25]。针对GRACE月时变重力场模型的误差特征和演变特性，本文结合EOF和MSSA两种方法的互补性，在利用EOF对球谐系数矩阵实现降噪和去冗余的基础上，进一步利用MSSA提取隐藏在EOF混叠模态中的非线性倾向和周期信号特征，以期有效构建可以准确描述GRACE离散时变重力场的大尺度动态变化模型。

1 数据处理

本文采用的GRACE数据为CSR(center for space research)提供的2002年8月至2016年8月共153个月的RL05版本时变重力场模型，球谐系数截断到60阶，其中潮汐、大气和海水质量变化的影响均已采用模型扣除。对GRACE月时变重力场模型作如下处理：采用卫星激光测距测得的更为准确的C20项对其作替换[26]；采用GRACE和海洋模型数据解算的一阶项加回到球谐系数中[27]；对球谐系数时间序列中16个月的缺测值采用最小二乘拟合作插补；从模型中扣除时间段内球谐系数的平均值；为削弱模型中高阶项球谐系数噪声的影响，采用300 km高斯滤波对其做平滑处理[2]；经过高斯滤波处理后，某些固定次的球谐系数的偶(奇)数阶之间仍存在明显的系统相关误差，这会导致GRACE反演结果在空间上呈现出显著的南北条带噪声。为此，对以上处理得到的169个月的时变重力场模型构成的去中心化的球谐系数矩阵，见式(1)

(1)

采用EOF分别将其分解成相互正交的空间特征向量和空间主成分的乘积之和，见式(2)

(2)

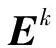
通过显著性检验选取其前几个空间主成分即可有效反映时变重力场模型的主要信号变化特征。这可起到两方面的作用：①有效消除球谐系数中高阶项系数存在的显著系统相关误差，提取其更优信噪比的信号[15-16]；②有效降低球谐系数矩阵空间维数的同时可显著减少后续MSSA的计算量。

对于式(2)中通过显著性检验的S-PC构成的多维时间序列xlt，其中l=1,2,…,L是通道序号，t=1,2,…,T是时间序号，包含了多种模态的混叠信号。为此，进一步利用MSSA提取隐藏在xlt中的非线性倾向和周期信号[28]。首先，把去中心化的xlt在时间迟后相空间排列，构建得到轨迹矩阵X，其第i+1列，也就是第i+1个状态向量为

Xi=(x1i+1,…,x1i+M,…,xLi+1,…,xLi+M)

(3)

式中，i=0,1,…,N-M；后迟量M称为窗口长度。

然后，对矩阵X作EOF分解，其分量形式为

(4)

(5)

MSSA最重要的应用功能是通过重建成分RC(reconstructed component)实现的，并由此从被分析对象中提取出与某个或某些特征成分相联系的部分[29]。根据最小二乘原理，由第k个特征成分得到的重建成分为

(6)

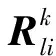
(7)

2 计算结果

2.1 EOF分解

对球谐系数矩阵ZC和ZS分别作EOF分解，以对系数矩阵进行降维和除噪。图2给出了前50个S-EOF的方差贡献，可以看出方差较大的值主要集中在前面几个且递减速度很快。依次对S-PC进行柯尔莫诺夫-斯米尔诺夫检验，结果表明在95%的置信水平下，ZC和ZS前7个特征值中除第6个以外均通过了显著性检验，相应的累积方差分别达到92.8%和91.0%。

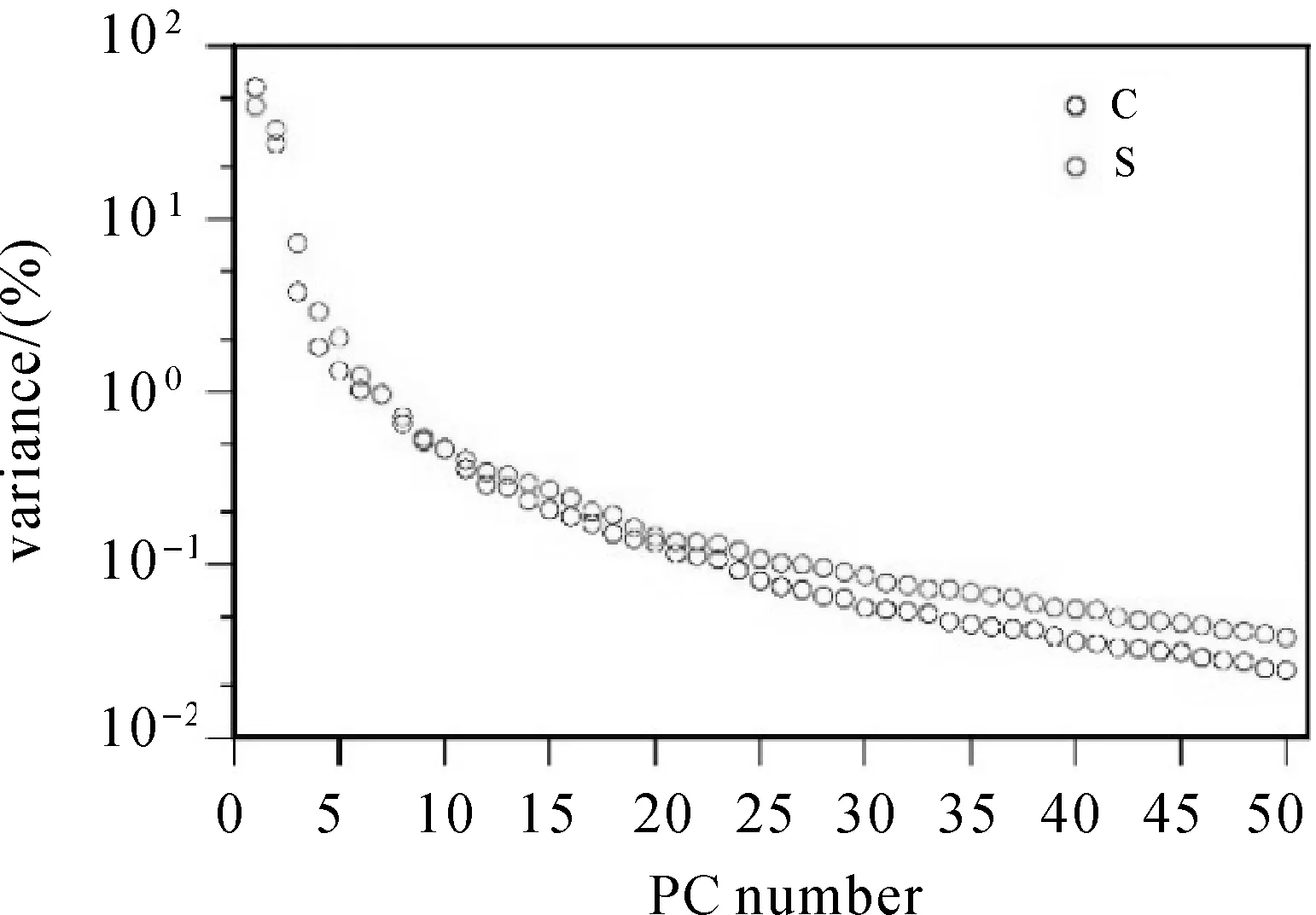
图2 前50个S-PC的方差贡献Fig.2 The eigen value spectra of the first 50 S-PC

选取通过显著性检验的S-PC和S-EOF重建统计量ZC和ZS，并由此反演全球陆表网格的等效水柱高变化时间序列。为了说明EOF的除噪效果，图3比较分析了经高斯滤波和“高斯滤波&EOF”处理后GRACE反演的2008年6月的全球陆表水储量变化结果。可以看出，只经过高斯滤波处理后的反演结果在两极地区的条带噪声尽管有所减弱，但在赤道两侧地区依旧比较明显；而经过“高斯滤波&EOF”处理后的条带噪声明显减少，且局部地区的信号变化得到有效呈现。另外，本文进一步比较分析了经“高斯滤波&EOF”和经验性的“高斯滤波&P5M11”[3-4]处理后的GRACE反演结果。图4对应给出了两种反演结果与GLDAS Noah水文模式(经高斯滤波处理)全球陆表之差的标准差序列。整体上看，“高斯滤波&EOF”要小于“高斯滤波& P5M11”处理后的标准差结果，相应的平均标准差分别为6.1和6.3 cm，从以上比较可以看出，EOF分解可有效消除GRACE球谐系数中系统相关误差的影响，提取其更优信噪比的信号。

图3 GRACE 反演的2008年6月全球陆表水储量变化Fig.3 The terrestrial water change recovered from GRACE in June 2008

图4 GRACE反演结果与GLDAS Noah之差的标准差Fig.4 The standard deviation of the differences between GRACE and GLDAS Noah

2.2 季节性变化

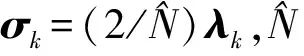
图5 前50个ST-PC的方差贡献Fig.5 The eigenvalue spectra of the first 50 ST-PC

图6给出了第2个和第3个特征值对应的ST-EOF和ST-PC。据图5，特征值2与3接近相等，同时满足|λk-λk+1|≤min{σλk,σλk+1}，且两个特征值对应的ST-EOF和ST-PC呈现出显著的周期性变化并相互正交。根据文献[29]，ST-EOF2&3可构成一对潜在的周期振荡模态，两者的总方差贡献可达到50.6%。

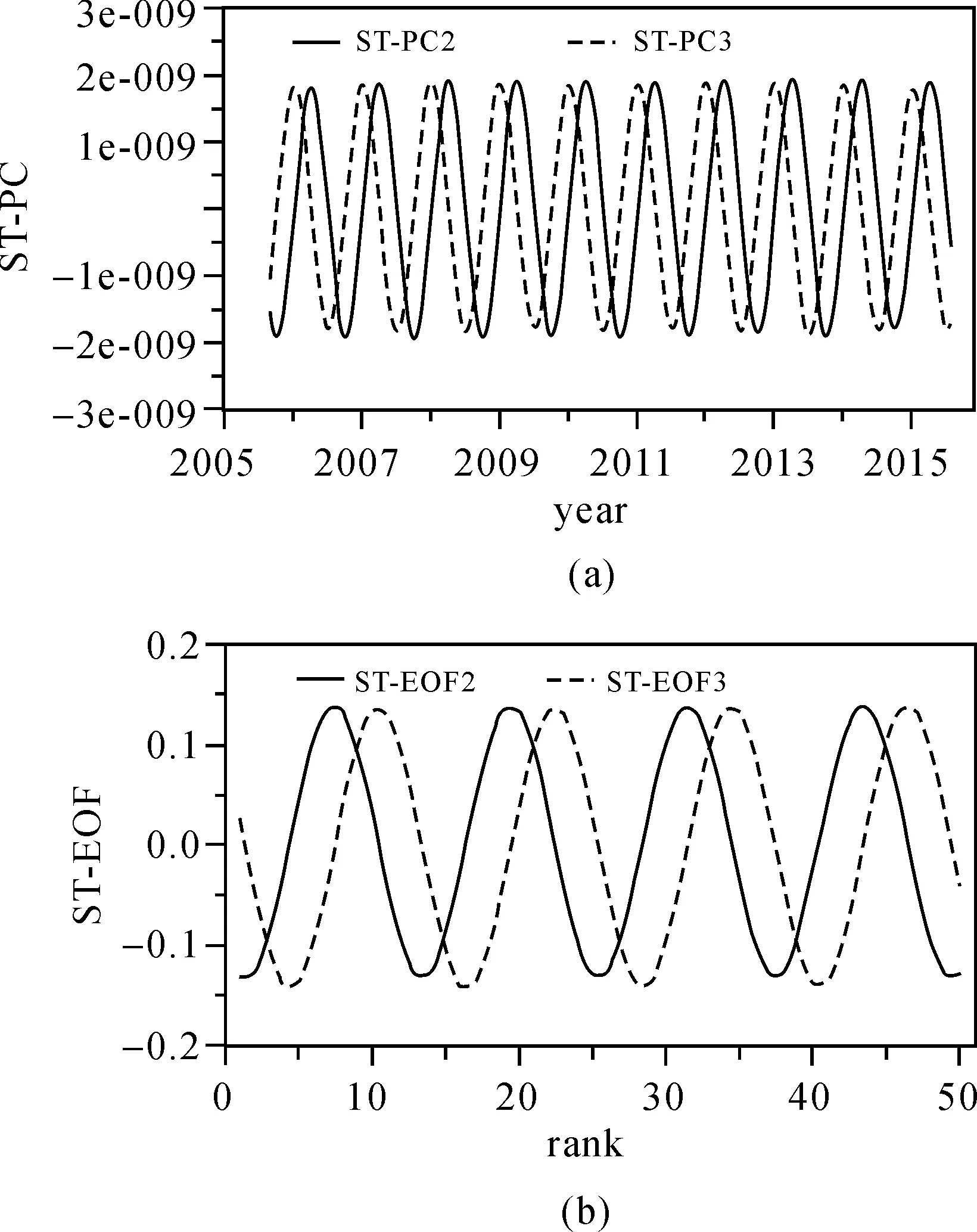
图6 第2个和第3个周期振荡模态ST-EOF及其对应的ST-PCFig.6 The second and third ST-EOF and ST-PC

采用ST-EOF2&3和ST-PC2&3重建MSSA分析对象RC，即对S-PC序列的拟合。选取RC方差最大的通道序列做最大熵谱估计，结果表明ST-EOF2&3为周期12个月的周年振荡模态。进一步由RC计算GRACE球谐系数的周年变化成分STRC(spatial-temporal RC)，并由此反演全球陆表网格的等效水柱高变化时间序列。图7给出了全球陆表水各网格的周年振荡最高相位与最低相位对应的差值结果。可以看出，陆表水周年振荡变化较大的区域主要位于赤道两侧，其中亚马孙流域最大可达99.7 cm。

为进一步分析陆表水的周年振荡变化特征，选取RC方差最大的通道序列，采用位相划分讨论方法，取各个位相陆表水各网格点的平均值得到周年振荡第1-8位相合成图(图8)。由图8可知，前后4个位相的正负距平分布基本相反。其中，第2位相和第3位相在中纬度地区呈现较大正值，在赤道地区呈现较大负值，而第6位相和第7位相则与之相反，反映出南北半球陆表水的季节性交替变化特征。

2.3 年际性变化

对矩阵ZC和ZS，通过显著性检验的S-PC时间序列做MSSA分析之前，为避免周年项成分对年际信号提取的干扰，首先将其从S-PC中作扣除。图9给出了前50个ST-EOF的方差贡献。可以看出，在误差范围内前50个特征值有2个达到95%的置信水平，相应的累计方差达到77.4%。

图10给出了第1个和第2个模态ST-EOF及其对应的ST-PC。可以看出，前两个ST-PC表现出一定的倾向特征，其方差贡献分别达到64.5%和12.9%。由于资料相对较短，目前还很难对两者长期变化的演变趋势作出判定。

采用ST-EOF1&2和ST-PC1&2分别重建GRACE球谐系数的长期趋势变化成分，并据此反演全球陆表网格的等效水柱高变化时间序列。图11对应给出了两者由一元线性回归估算的全球陆表水变化趋势。可以看出，受降水、地下水损耗和冰川消融等的影响，本文给出的两种趋势信号的空间分布与以往的研究结果基本类似[30-33]。另外，受冰川均衡调整的混叠影响，北美哈德逊湾、斯堪的纳维亚半岛和西南极等地区呈现出较为显著的质量增加信号[34-35]。

2.4 动态变化模型

基于EOF&MSSA重建的“周年项分量+趋势项分量”构建得到GRACE球谐系数(Clm,Slm)的非线性模型STRCnonlinear。为从频谱域上说明STRCnonlinear的拟合效果，以球谐系数(C10,1,S10,1)为例，图12比较分析了其变化时间序列与非线性模型。结果表明，本文构建的模型能较好拟合(C10,1,S10,1)时间序列的非线性变化特征，拟合标准差分别为1.9×10-12和2.0×10-12。图13进一步给出了EOF&MSSA得到的GRACE 60阶次球谐系数的拟合标准差分布。整体上该方法得到拟合标准差由低阶到高阶逐步递减，结果介于2.5×10-15～5.0×10-11，平均值为4.3×10-13。

图7 全球陆表水周年振荡最高与最低相位对应的差值Fig.7 The differences between extreme high and low phases of the annual oscillation

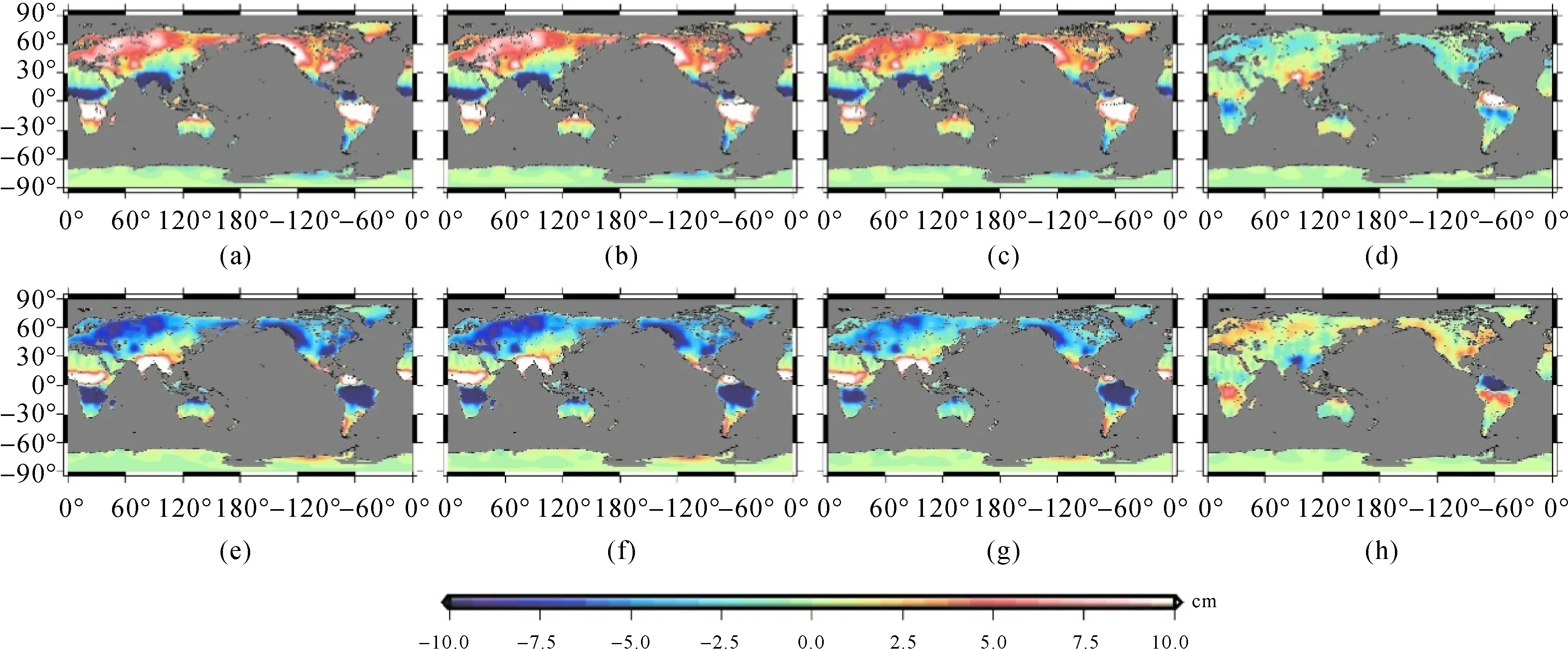
图8 陆地水周年振荡第1—8位相合成图Fig.8 Spatial structures of the terrestrial water annual oscillation keyed to eight phases

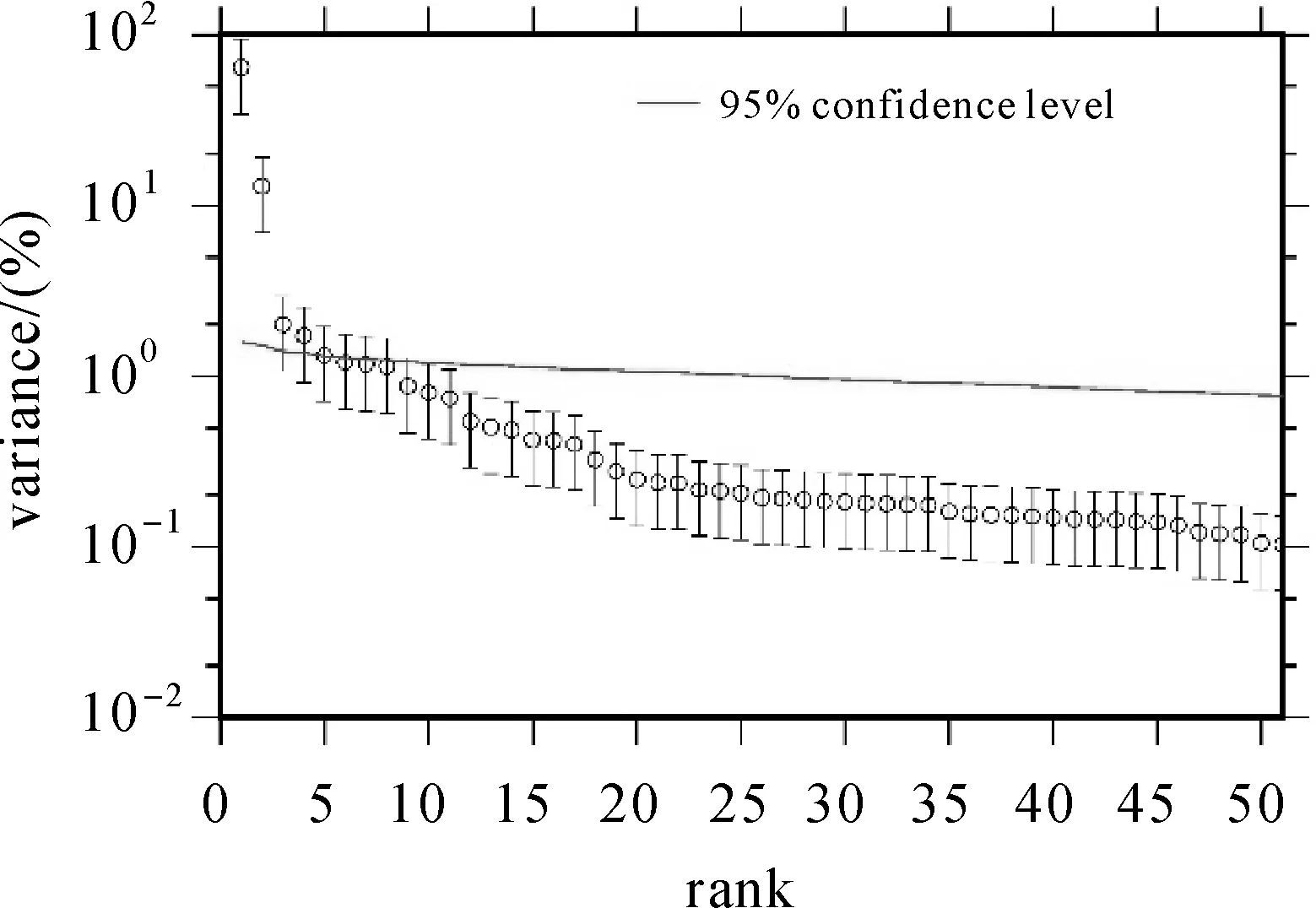
图9 前50个ST-PC的方差贡献Fig.9 The eigen value spectra of the first 50 ST-PC

为从空间域上说明STRCnonlinear的拟合效果，本文进一步比较分析了EOF&MSSA和最小二乘拟合法(考虑趋势项和周年项，对只经过高斯滤波和EOF处理后的60阶次的球谐系数时间序列逐个做拟合计算) 反演得到的全球等效水柱高变化结果。以陆地水变化较为显著的亚马孙流域(2.5°S,58.5°W)和南极半岛(75.5°S,98.5°W)为例(图14)，EOF&MSSA和最小二乘拟合法得到的两个网格点上等效水柱高的拟合标准差分别为13.6和15.1、9.6和10.1 cm，相比而言，EOF&MSSA构建的非线性模型能更好地反映两个区域等效水质量的动态变化特征。图15进一步给出了全球陆表共21 334个网格点上的拟合统计结果，结果表明，EOF&MSSA得到的拟合标准差介于0.3～14.0 cm，平均标准差为1.8 cm，而最小二乘拟合法的结果介于0.3～15.1 cm，平均标准差为1.9 cm，且在69%的网格点上EOF&MSSA得到的拟合标准差要小于最小二乘拟合法的结果，整体上可以看出EOF&MSSA构建的非线性模型能更好地拟合GRACE离散球谐系数的动态变化特征。需要指出的是，以上结果分别是由EOF&MSSA对12个S-PC构成的多维时间序列和最小二乘拟合法对3720个球谐系数时间序列拟合得到的结果。因此，与最小二乘拟合法相比，EOF&MSSA在显著减少系统相关误差和计算量的同时即可取得更好的拟合精度，反映出其在提取和构建GARCE球谐系数大尺度动态变化模型方面的优越性。

图10 第1个和第2个模态ST-EOF及其对应的ST-PCFig.10 The first and second ST-EOF and ST-PC

图11 全球陆表水等效水柱高变化趋势Fig.11 The terrestrial water change trend

图12 GRACE球谐系数及其非线性模型变化时间序列Fig.12 GRACE SHCs time series and its nonlinear model

图13 GRACE 60阶次球谐系数与其非线性模型之差的标准差Fig.13 The standard deviation of the differences between GRACE SHCs and its nonlinear model

图14 EOF&MSSA法和最小二乘拟合法反演得到的等效水柱高时间序列Fig.14 The time series of equivalent water heights from EOF&MSSA and least square method

图15 全球陆表网格点等效水柱高的拟合标准差Fig.15 The fitting standard deviation of equivalent water heights on grids over global land areas

另外，从图13和图15全球尺度上的结果来看，本文采用EOF&MSSA构建的非线性模型对GRACE球谐系数及其反演结果仍存在一定的拟合差异。从局部尺度上看，这种拟合差异可能主要来源于两个方面：①受多种误差因素的影响，GRACE高阶项球谐系数观测精度相对较差，这较大干扰了直接从球谐系数提取ENSO、北极涛动/北大西洋涛动等气候模态引起的区域陆地水文信号变化[23,36-37]；②受某些区域极端干旱、洪涝等气候因素的影响，GRACE球谐系数会存在一些异常信号，这会进一步干扰对球谐系数变化的拟合精度[38-39]。由此可以看出，目前GRACE重力卫星获取的离散时变重力场模型的精度未来仍有提升空间。

3 结 论

针对GRACE月时变重力场的误差特征和演变特性，提出联合经验正交分解和多通道奇异谱分析的方法，提取、分析其动态变化特征并构建了相应的非线性变化模型。相比经验性的去相关滤波方法，EOF对GRACE月球谐系数实现空间压缩的同时可有效去除系统相关误差的影响，提取其更优信噪比的信号。多通道奇异谱分析的提取结果表明，GRACE离散球谐系数存在显著的长期趋势项和周年项变化成分，其中，周年项模态的方差贡献达到50.6%，扣除周年项成分后长期趋势项的累积方差贡献达到77.4%。以EOF&MSSA提取的长期趋势项和周年项成分构建了GRACE离散球谐系数的非线性模型，其拟合标准差介于2.5×10-15～5.0×10-11，平均标准差为4.3×10-13，其对全球陆表等效水柱高的拟合标准差介于0.3～14.0 cm，平均标准差为1.8 cm。相比传统的最小二乘拟合方法，EOF&MSSA在显著减少系统相关误差和计算量的前提下即可在频谱域和空间域上更好地拟合GRACE离散时变重力场模型的大尺度动态变化特征。

从本文的研究结果看，目前GRACE重力卫星获取的时变重力场的精度未来仍有提升的空间。随着下一代重力卫星的GRACE FO发射，借助其更高时空分辨率的球谐系数数据，有望为离散时变重力场各种参量的动态变化模型构建及其在全球气候变化、地球动力学等中的应用提供重要参考。