混凝土内部界面过渡区脱开过程的扩展有限元模拟*

房宁志 夏晓舟 章 青

(河海大学力学与材料学院 南京 211100)

0 引 言

混凝土微观结构实验[1-2]和数值模拟[3-4]结果均表明：混凝土中骨料和水泥砂浆基体之间存在着物理力学性能截然不同的界面过渡层.界面过渡区对混凝土材料的宏观力学性能及其破坏过程都有很大影响.考虑到界面过渡区对混凝土宏观力学性能的决定性影响，数值模拟必须在细观层面上展示混凝土内部骨料界面过渡区的弱连接行为.最直观的策略就是在骨料和水泥砂浆之间嵌入黏聚单元(cohesive element)[5]，并赋予黏聚单元的力-分离本构行为，以实现界面过渡区的黏聚脱开模拟；但嵌入cohesive单元的方法涉及复杂的网格剖分和嵌入处理.基于扩展有限元方法[6]中材料内部的物理界面(含裂纹)的演变过程可在固定的有限元网格下实现的优势，本文在扩展有限元法(XFEM)的框架下，引入强间断的位移扩充形函数以及界面力-界面相对位移的本构描述来反映界面过渡区的传力和变形特点[7]，建立混凝土试样的界面过渡区扩展有限元模型，以实现混凝土试样在荷载作用下界面过渡区从粘聚到逐步脱开的全过程仿真.在此基础上，进行平均化处理，估算出混凝土材料的宏观体积模量和宏观剪切模量，并进一步探究界面过渡区的力学行为对混凝土的宏观力学特性的影响规律.

1 混凝土细观扩展有限元法建模

1.1 单元位移模式

XFEM的核心思想是在传统有限元法的单元位移模式中引入能够反映裂纹或材料界面对变形影响的扩充项，即

(1)

式中：x为空间坐标；u为单元内x点的位移；NI为标准形函数；uI为单元结点位移；φJ为反映不连续性的扩充形函数；qJ为加强结点的附加位移.对于混凝土内部界面过渡区，大部分学者按弱连续模式定义其扩充形函数[8]为

φJ=NJf(x)

(2)

式中：f(x)是水平集函数，定义为

(3)

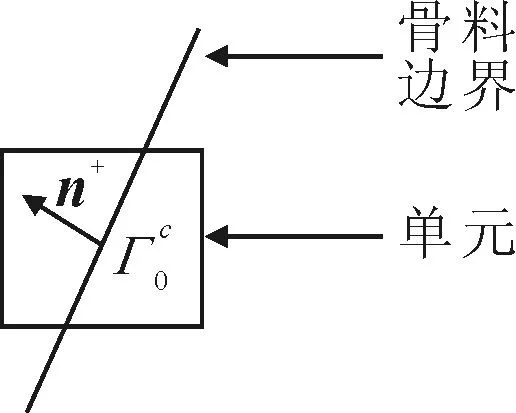
图1 贯穿单元

为此，本文采用强不连续的位移模式来反映界面过渡区的相对位移，其扩充形函数定义为

φJ=NJH(f(x))

(4)

式中：H(x)为阶跃函数，定义为

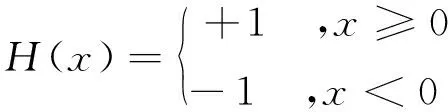
(5)

这种强不连续的位移模式要求界面过渡区的本构模型必须纳入到界面力-界面相对位移关系的框架下进行描述.

1.2 界面过渡区的粘聚脱开行为

当界面应力达到界面强度时，界面开始损伤，进入界面断裂能释放阶段，至完全脱开，界面处的应力为零.与裂纹不同的是：界面处位移虽然不连续，但能传递力，假定骨料界面力-界面相对位移满足双线性关系，见图2，引入损伤变量，使双线性关系统一成一个表达形式，即

(6)

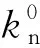
(7)

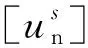
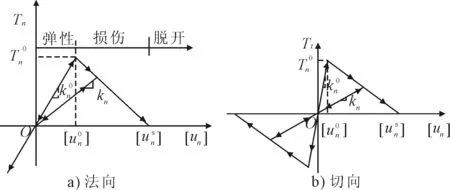
图2 界面力与界面相对位移之间的关系

1.3 反映界面过渡区特性的扩展有限元列式

1.3.1控制方程

(8)

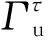
图3 界面问题中的各类边界条件示意

1.3.2积分弱解形式

试探函数空间定义为

(9)

测试函数(权函数)空间定义为

U0={δu(x)|δu(x)∈C0,δu(x)=0

(10)

代入几何方程和本构方程，则弱解形式可表述为

(11)

式中：D为弹性矩阵.

1.3.3区域离散化

对式(11)进行区域离散化，即

(12)

式中：Ne为单元总数目；[u]为骨料界面相对位移.根据位移模式(1)和式(4)，获得

[u]=nA(uA-uB)=

nANae(h(d(xA))-h(d(xB)))

(13)

将式(1)和(13)式代入式(12)，获得

(Nφ)TF)dΩ+

gDcohnAN(h(d(xA))-h(d(xB))aedΓ=0]

(14)

将单元结点自由度用结构结点自由度为

ue=guu,ae=gaa

(15)

式中：gu,ga为选择矩阵.所以式(14)化为

(16)

令：

所以，离散方程的弱解形式(15)式可写为

δW=δuT(Kuuu+Kuaa-fext)+

(17)

因为δu、δa是任意的，所以式(17)等价为

(18)

化为矩阵形式：

(19)

由于骨料界面力与界面位移之间的关系是非线性的，因此上式改为增量形式，即

(20)

1.4 单元积分方案

对于含界面过渡区的扩展有限元单元，由于涉及骨料和水泥砂浆等多种材料，单元积分不能按照高斯积分的策略进行，即便是加密高斯积分点[9]，也会引起较大的积分误差，而必须按材料子域进行积分[10-11].本文采用材料子域的三角形子划分策略，在每个三角形子划分中按Hammer积分进行，见图4.

图4 三角形子域积分示意图

当界面过渡区与网格边界或网格结点靠得很近时，其子划分可能会导致某些三角形面积过小或形状过于尖锐，从而降低积分精度，为此，本文采用了网格局部调整的策略以确保高精度积分，见图5.

图5 网格节点调整

2 数值算例

2.1 中心含圆骨料的平板分析

2.1.1可靠性验证

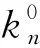
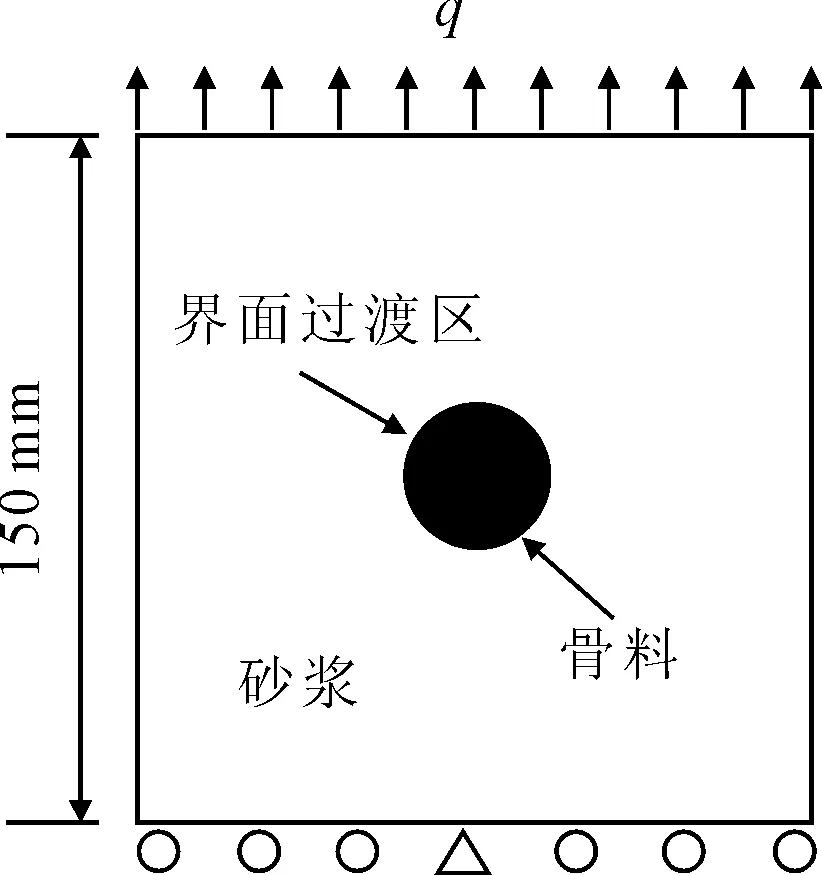
图6 圆夹杂板单轴拉伸

q=3 MPa时两种数值方法得到的竖向应变云图见图7，由图7可知，二者分布基本相同，最大竖向应变分别为1.38×10-4和1.37×10-4，相差甚微.q=21 MPa时骨料界面过渡区的法向相对位移见图8，由图8可知，骨料的顶部和底部已脱开，二者的法向相对位移也十分接近.验证了本文扩展有限元模型的可靠性.

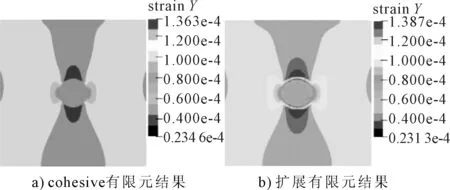
图7 竖向应变分布对比

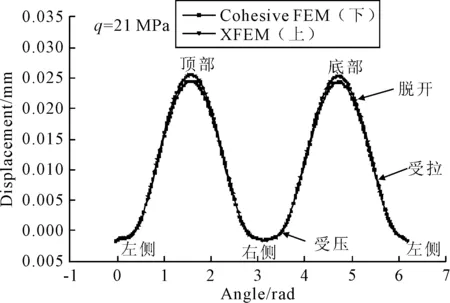
图8 圆形骨料界面过渡区的法向相对位移

2.1.2界面过渡区的损伤脱开状态分析

为追踪界面过渡区的损伤脱开过程，对图6中平板上部逐步施加均布荷载q.取q=6，12和21 MPa时的竖向应变云图，见图9，由图9可知，随着均布荷载的增加，界面过渡区相对位移逐渐w增大，变形局部化特征愈发明显，当q达到21 MPa时，骨料顶部和底部的界面过渡区出现大范围的脱开，高应变区集中在骨料周围.

图9 应变随荷载变化的演变

在荷载q=21 MPa作用下界面过渡区的法向应力和切向应力见图10，由图10可知，法向应力呈对称分布，而切向应力呈反对称分布，且顶部大部分应力都已释放，处于完全脱开状态，但骨料两侧处于受压状态，且相互侵入，侵入量见图8左右两侧出现的相对位移负值，界面的初始法向刚度取得越大，侵入量就越小，就越接近实际情况.

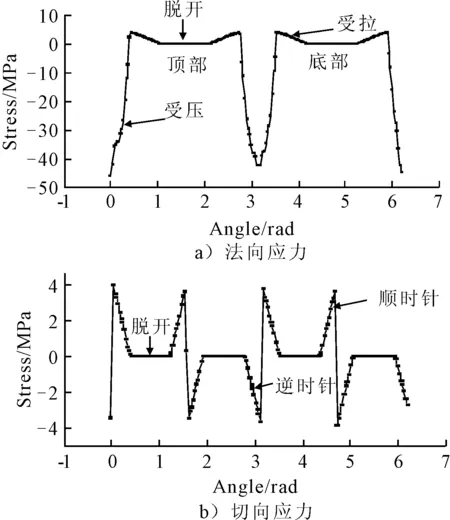
图10 圆形骨料界面过渡区的法向和切向应力

2.2 混凝土试样受拉分析及宏观模量的估算

以二级配混凝土为例，按级配理论在试样中随机分布大、小椭圆骨料，骨料体积分数为31%.上部均布荷载q逐步施加到15 MPa时获得混凝土试样的竖向应变云图见图11，由图11可知，大骨料的界面脱开位移大于小骨料的界面脱开位移，与实验结果相同.

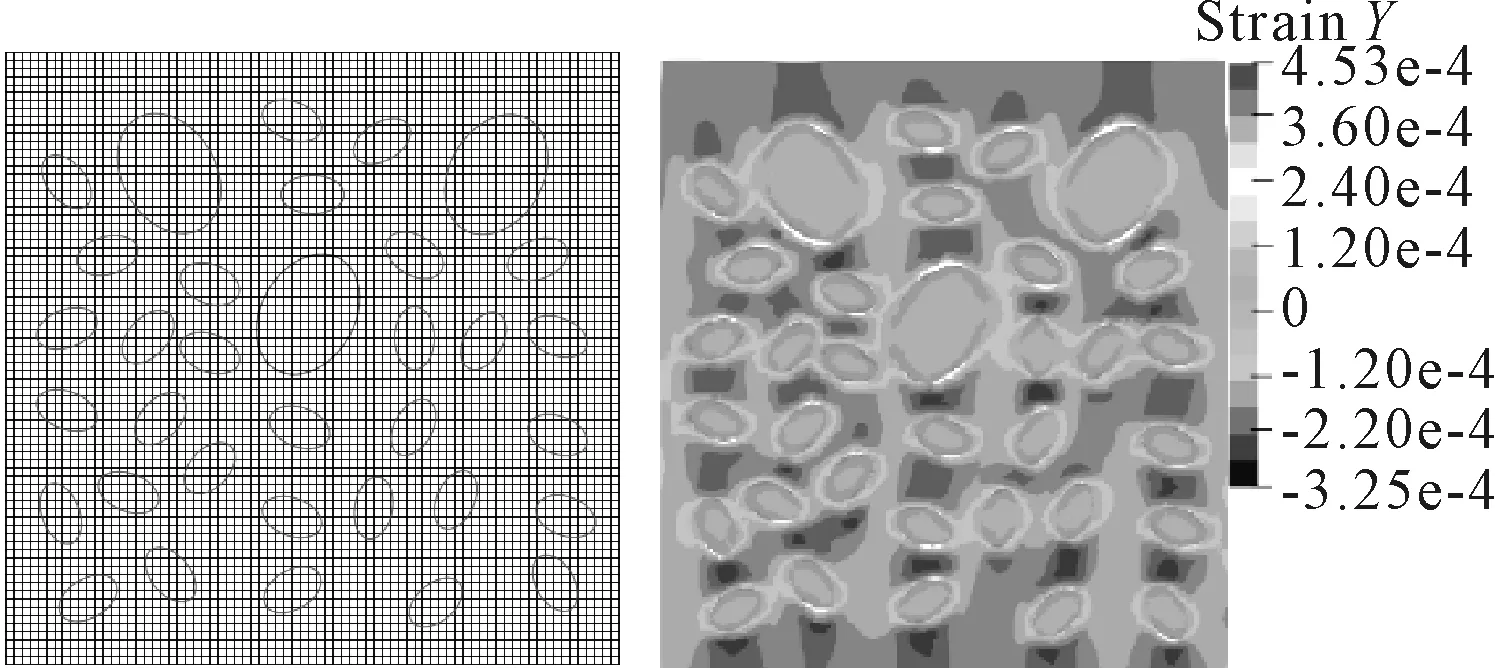
图11 二级配混凝土网格模型与竖向应变云图

为进一步分析界面过渡区性质对混凝土宏观力学性能的影响，提取数值计算结果，在应变能等效的原则下，估算出混凝土宏观的体积模量和剪切模量，见表1～2.

表1 混凝土细观各组份的体积模量和剪切模量

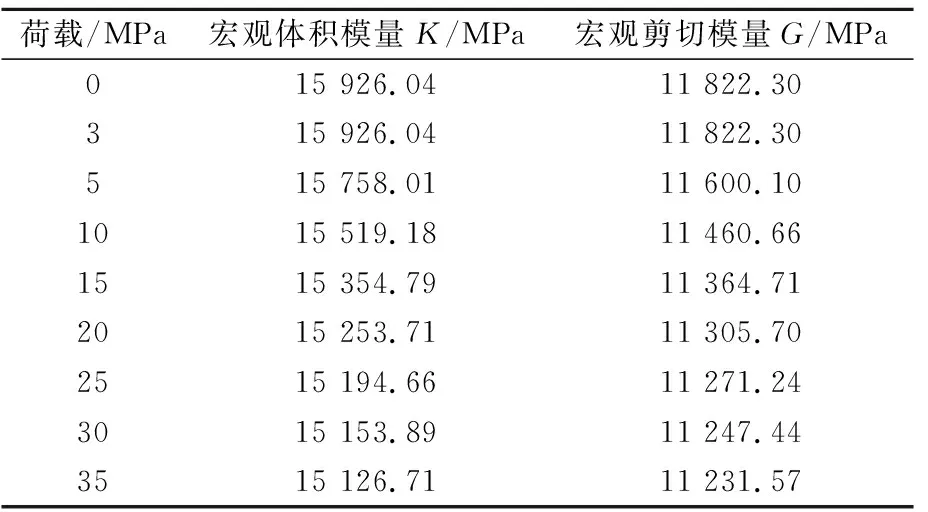
表2 随荷载变化模量变化(界面刚度=10×104 MPa/mm)

由表2可知，当荷载达到3 MPa时，界面进入应力释放状态，此后，随着荷载的增加混凝土的宏观体积模量K和宏观剪切模量G而减小，当荷载达到20 MPa之后，宏观体积模量K与宏观剪切模量G减小更为明显，体现了界面过渡区对混凝土宏观力学性能的削弱效应.

表3为界面初始刚度对混凝土宏观有效模量的影响，由图3可知，混凝土宏观体积模量K和剪切模量G随初始界面刚度的增加而增大.当初始界面刚度超过5×107MPa/mm时宏观模量增加不明显.

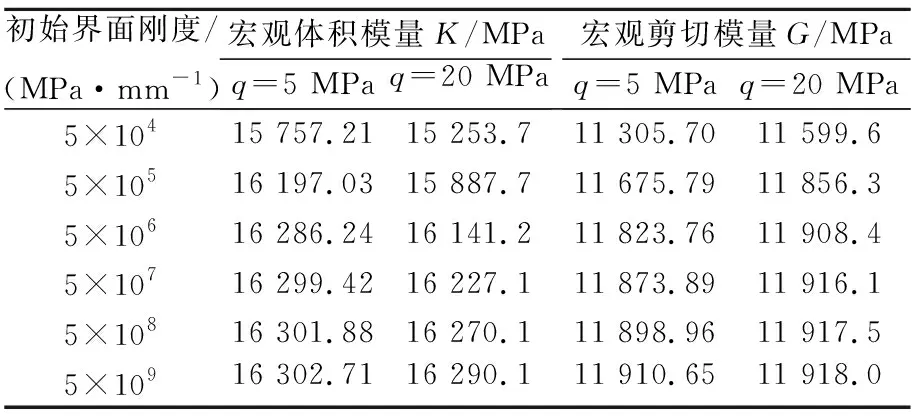
表3 混凝土宏观模量随界面刚度的变化规律

3 结 论

1) 建立的混凝土细观扩展有限元模型由于采用了力-分离的本构描述模式来反映界面过渡区的力学特性，使得强不连续的位移模式能够把界面粘聚、损伤和完全脱开三种状态统一起来，无需进行弱不连续到强不连续的切换，就能在扩展有限元框架下实现界面过渡区从粘聚到脱开的全过程仿真.

2) 扩展有限元的最大优势就是求解域中的物理边界(如界面过渡区、裂纹)始终独立于有限元网格，这使得有限元网格划分变得简单而规整，且单元精度要高于三角形或四面体单元精度.网格划分的优势虽然对二维细观模拟不是很明显，但对三维细观模拟将展示其巨大的潜力.

3) 对混凝土宏观体积模量和剪切模量随界面过渡区的初始刚度增大而增大，当初始界面表刚度超过5×107MPa/mm时，无论是初始粘聚还是后期损伤或脱开状态，宏观模量的增大都不是很明显.实际上，界面过渡区处于粘聚状态时是没有相对位移的，当初始界面刚度取得越大，粘聚状态的相对位移就越小，取到无穷大时，粘聚相对位移为零，消除了粘聚状态的误差，但另一方面又加剧了线性方程组的病态性，导致求解的收敛速度变慢.