温度荷载和车辆载荷作用下CRTSⅢ无砟轨道板损伤分析*

李 岩 赵春发 朱胜阳

(西南交通大学牵引动力国家重点实验室 成都 610031)

0 引 言

无砟轨道具有高平顺性、高稳定性、长寿命和少维修等优点，在我国高速铁路工程中得到广泛应用.但是，作为一种刚性混凝土承载结构，无砟轨道一旦出现局部破损、轨道板断裂、砂浆层脱离和碎裂等损伤问题，很难整治，维修成本高，并影响列车正常运营.近年来，随着我国高速铁路运营里程和运营时间的增长，上述结构性损伤与破坏已逐渐显现，对高速列车行车安全造成隐患，迫切需要采取合理的防控措施[1-2].其中，CRTS Ⅲ型无砟轨道是我国研发的具有完全自主知识产权的板式无砟轨道，已成功应用于郑徐、京沈、商合杭等十余条高速铁路，今后在我国后续高速铁路建设和铁路“走出去”中将得到更广泛的应用.因此，我国有必要加强CRTS Ⅲ型无砟轨道损伤特性的研究，为其技术提升与进一步推广应用提供理论支撑.

目前，国内针对板式无砟轨道力学行为的研究比较广泛，但主要侧重于温度梯度荷载[3-4]、车辆动荷载[5]或路基不均匀沉降作用下[6]轨道结构应力-压力-应变状态分析，很少考虑日温场和车辆荷载作用下轨道结构损伤及其对轨道结构动力性能的影响.已有的轨道结构损伤特性研究多采用了线弹性模型，杨俊斌等[7]基于弹性地基梁-体模型，研究了CRTS I型轨道板以及CA砂浆层在车辆荷载作用下的疲劳损伤.林红松等[8]基于线弹性断裂力学理论，建立了考虑道床裂纹的无砟轨道有限元模型，对车辆静荷载作用下的无砟轨道进行了受力分析.以上研究为高速铁路无砟轨道技术开发与应用提供了有益参考，但对于运营过程中温度荷载和车辆荷载共同作用下无砟轨道板的损伤行为与演化特征还缺少较为深入的研究.

为了更准确反映轨道板的拉压异性以及损伤特性，本文建立了基于混凝土塑性损伤模型的CRTS Ⅲ型板式无砟轨道有限元模型.首先，利用某地夏季现场实测温度场数据，开展了无砟轨道三维瞬态热传导分析，并以此为基础数值模拟轨道板在变温作用下的损伤行为.其次，运用车辆-轨道耦合动力学理论与方法计算车辆动荷载，模拟了温度荷载和车辆动载荷共同作用下CRTS Ⅲ型板式轨道板的损伤行为，并对比分析了车辆荷载通过有、无损伤轨道板时的动力学响应.

1 混凝土损伤塑性模型

1.1 本构关系

混凝土损伤塑性模型的弹塑性特性通过有效应力和硬化变量来描述

(1)

(2)

(3)

(4)

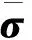
1.2 混凝土的损伤与刚度退化

混凝土的单轴受拉特性是典型的理想弹塑性模型，见图1.在受拉达到屈服应力之前表现为线弹性，之后直接进入软化下降段，并伴随着刚度的退化，下降段描述了后续破坏和开裂应变的关系，开裂应变计算式为

(5)

塑性应变计算式为

(6)

式中：dt为单轴受拉损伤因子.

图1 拉伸开裂应变

混凝土的单轴受压特性是弹塑性硬化模型，其应力应变关系见图2.

图2 压缩非弹性应变

在受压达到屈服应力σc0之前表现为线弹性，之后进入硬化阶段，屈服应力继续增大，当应力达到极限应力σcu之后，才是软化下降段.其中硬化数据由非弹性应变表示，非弹性应变计算式为

(7)

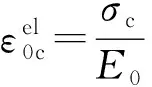
塑性应变公式为

(8)

式中：dc为单轴受拉损伤因子.

因此，混凝土受拉和受压的应力-应变关系可以分别表示为

(9)

(10)

混凝土在受压或受拉时造成损伤，弹性模量从初始E0退化为E，刚度退化系数d为应力状态和单轴损伤因子dt和dc的函数

E=(1-d)E0(0≤d≤1)

(11)

1-d=(1-stdc)(1-scdt)

(0≤st,sc≤1)

(12)

式中：st和sc分别为与应力状态有关的参量，可用下式定义

(14)

式中：下标t和c分别代表拉伸和压缩过程；wt和wc分别表示材料在反向载荷作用下刚度恢复的权重因子，与材料特性相关.

2 轨道板损伤分析模型

2.1 CRTS Ⅲ型板式无砟轨道有限元模型

考虑轨道板中的横纵向钢筋，并采用嵌入单元技术将钢筋网整体移植到轨道板中，假设钢筋与混凝土之间接触良好，无相对滑移，各结构层之间接触属性利用Tie命令定义，生成图3所示CRTS Ⅲ型板式无砟轨道有限元模型.该模型在轨道结构、热学特性都确定的情况下，边界条件综合考虑太阳辐射、气温对流换热和结构表面辐射.

图3 CRTS Ⅲ型板式无砟轨道模型

根据热-应力顺序耦合分析方法，进行热应力分析时，将三维瞬态热传导分析模型更新为热应力分析模型.具体变化如下：以轨道结构的材料力学参数替换热力学参数；修改热传导模型中单元的定义，重新划分轨道板、自密实混凝土、底座板和基床表层；轨道板采用损伤塑性模型，其他结构均采用线弹性模型；解除三维瞬态热传导模型中的热边界条件和温度载荷，对模型底部施加固定约束，两端施加对称约束；最后设置正确的分析步，准确地读入温度场数据.

2.2 车辆动荷载计算模型

采用车辆-轨道耦合动力学理论[9]，建立了车辆-CRTS Ⅲ型板式无砟轨道耦合动力学模型，见图4.

图4 车辆-CRTS Ⅲ型板式无砟轨道耦合动力学模型

其中，轮轨垂向力采用Hertz非线性弹性接触模型，钢轨考虑为离散支撑的Bernoulli-Euler梁，轨道板考虑为连续弹性支撑的自由梁.车辆-轨道耦合动力学考虑了钢轨振动和变形对轮轨作用力的影响，能更真实地反映车辆与轨道之间的动力相互作用，已经在现场试验和实际工程应用中得到了很好的验证.

2.3 模型参数

采用某地夏季最炎热时期的实测温度和气象数据[12]和无砟轨道材料热力学参数，见表1.模拟轨道结构热传导分析的边界条件.

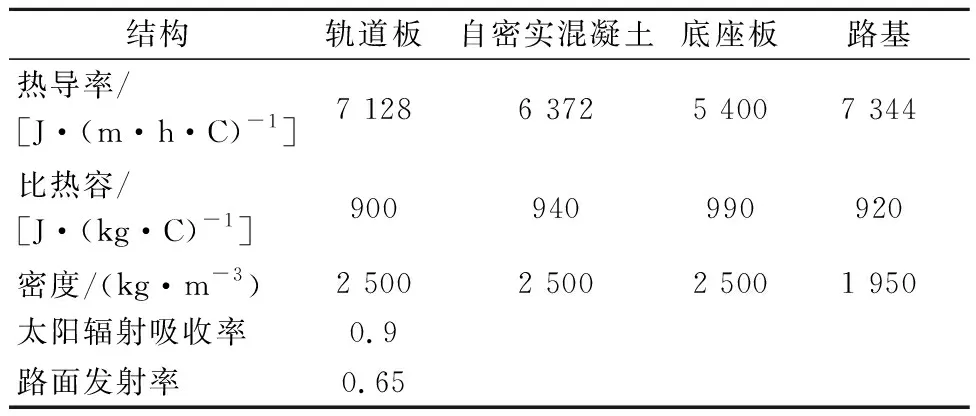
表1 CRTS Ⅲ型板式无砟轨道材料热力学参数

混凝土塑性损伤模型参数根据GB50010—2002《混凝土结构设计规范》来确定，损伤因子采用Sicliroff余能等效原理计算.

单轴受压损伤因子计算公式为

dc=1-

(15)

(16)

单轴受拉损伤因子计算公式为

(17)

(18)

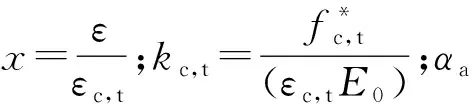
表2 CRTS Ⅲ型板式无砟轨道结构参数

表3 混凝土损伤塑性模型材料力学参数

注：Kc为拉伸子午面与压缩子午面第二应力不变量之比.

3 变温作用下轨道板损伤分析

对CRTS Ⅲ型板式无砟轨道结构进行三维瞬态热传导分析，得到轨道板上、下表面温度场一天24 h内的变化情况，见图5.温度场变化规律与CRTS Ⅱ无砟轨道轨道板结果[11]较为一致，说明计算结果可靠，可用于后续分析.计算结果表明，轨道板1 d之内经历了升温和降温两个温变过程，轨道板上表面的温度变化较大；上、下表面的实时温差最高可达24 ℃.1 d之中轨道板上表面的最高温度出现在13:00时，最高温度达到56.7 ℃.

图5 轨道板一天内温度变化曲线

为了考虑轨道板在降温过程中的受拉特性，将荷载施加顺序设置为先降温后升温，计算得到轨道板上表面中心的应力应变与损伤值，见图6.

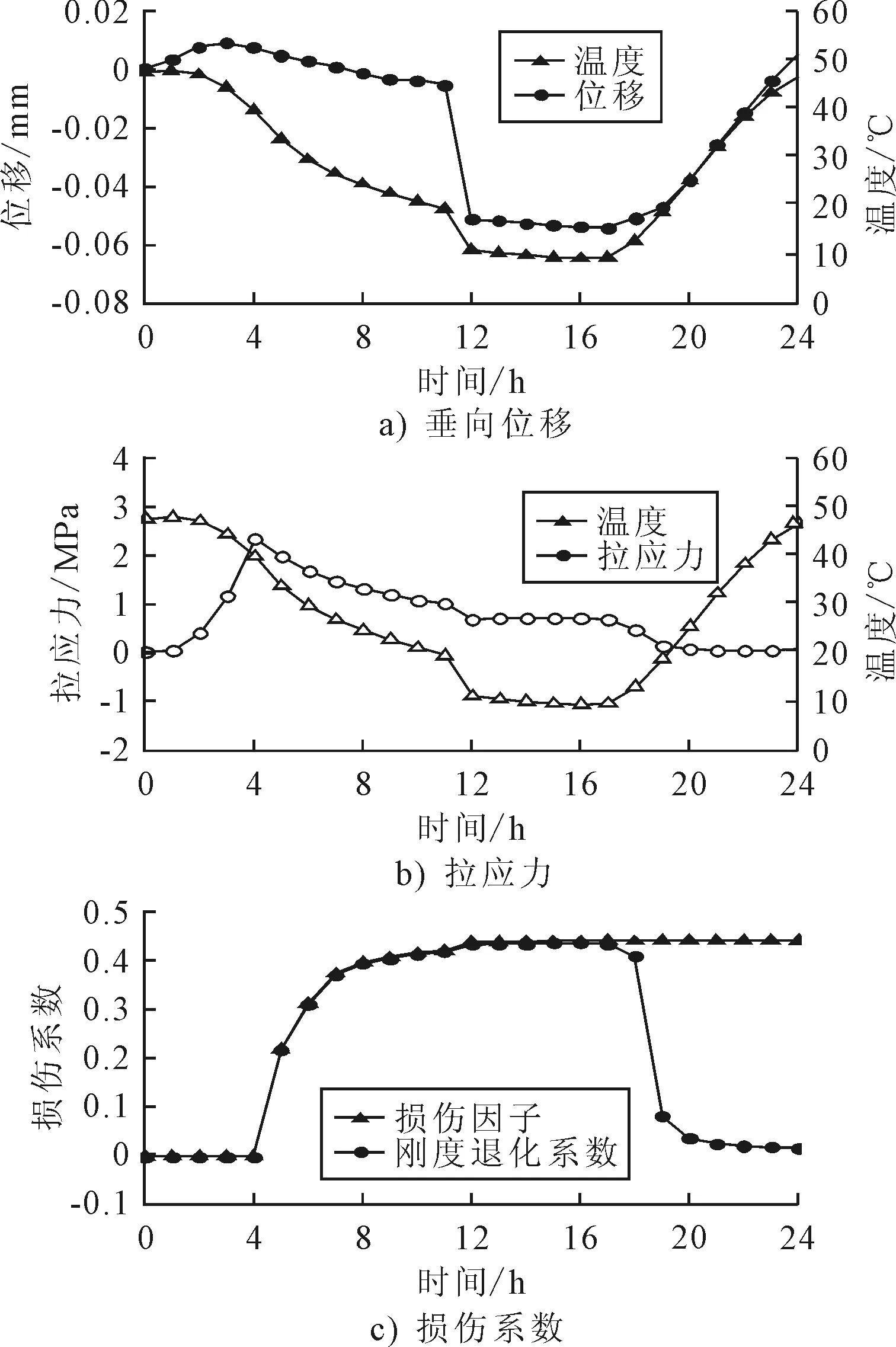
图6 变温作用下轨道板上表面应力应变与损伤

由图6 a)可知，在降温阶段，由于轨道板出现收缩变形，上表面中心出现下凹变形，变形量约0.05 mm.由图6 b)～c)可知，在持续降温4 h以后，轨道板上表面温度下降了5.1 ℃，由于收缩作用引起轨道板表面出现拉应力，上表面中心处拉应力超过C60混凝土的抗拉极限值2.08 MPa，此时拉伸损伤值和刚度退化系数均大于零，轨道板表面开始产生损伤；随着温度继续下降，轨道板应力特性呈现软化下降趋势，应力逐渐减小，但变形会继续增大，从而导致轨道板内部微裂纹增多，轨道板的有效承载面积减小，在破坏最严重的地方，损伤因子和刚度退化系数由零迅速增加至0.4左右.

由图6c)可知，当进入升温阶段后，轨道板的变形和拉应力逐渐减小为零，但轨道板上表面最大损伤因子仍保持在0.44的水平.刚度退化系数在变温作用17 h之后逐渐减小至零，说明轨道板内部微裂纹由张开的最大状态逐渐闭合，而轨道板在整个变温过程没有产生压缩损伤.

4 温度和车辆载荷作用下轨道板损伤分析

利用图4的车辆-轨道耦合动力学模型，计算得到钢轨扣件处支点反力，将其作为图3模型的输入荷载，可以模拟移动车辆荷载作用.计算车辆动荷载时，CRH2高速车辆的运行速度设为300 km/h，轨道不平顺采用中国高速铁路无砟轨道谱，波长范围为2～200 m.

将计算得到的扣件支点反力作为变温作用下轨道板处于最大损伤状态时的输入荷载，模拟分析CRTS Ⅲ型板式无砟轨道同时承受变温作用和车辆动荷载作用时的损伤力学行为.图7为车辆通过时轨道板中间左、右钢轨支点处的刚度退化系数.

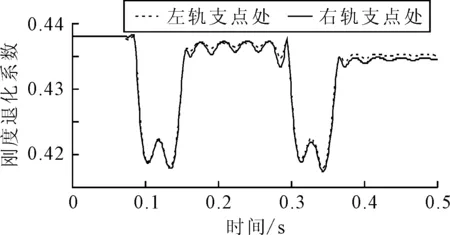
图7 扣件支点处轨道板刚度退化系数

由图7可知，车辆通过前，支点处轨道板的刚度退化系数为0.44(由变温作用引起)；车辆通过时，轨道板的刚度出现暂时恢复的现象，幅值变化约为0.02；车辆通过后，轨道板刚度退化系数仅有极微小的变化.可见，虽然在变温作用下轨道板已发生损伤，但在车辆载荷的进一步作用下，轨道板刚度退化系数基本不变，这说明在不考虑雨水渗透等因素时，车辆荷载并不会加剧轨道板的损伤，变温作用是轨道板产生损伤的主要根源.

进一步计算了CRTS Ⅲ型板式无砟轨道在经历变温损伤和不经历变温损伤后，在车辆荷载作用下的动力学响应，重点对板中扣件支点处的动力响应进行对比分析，见图8.

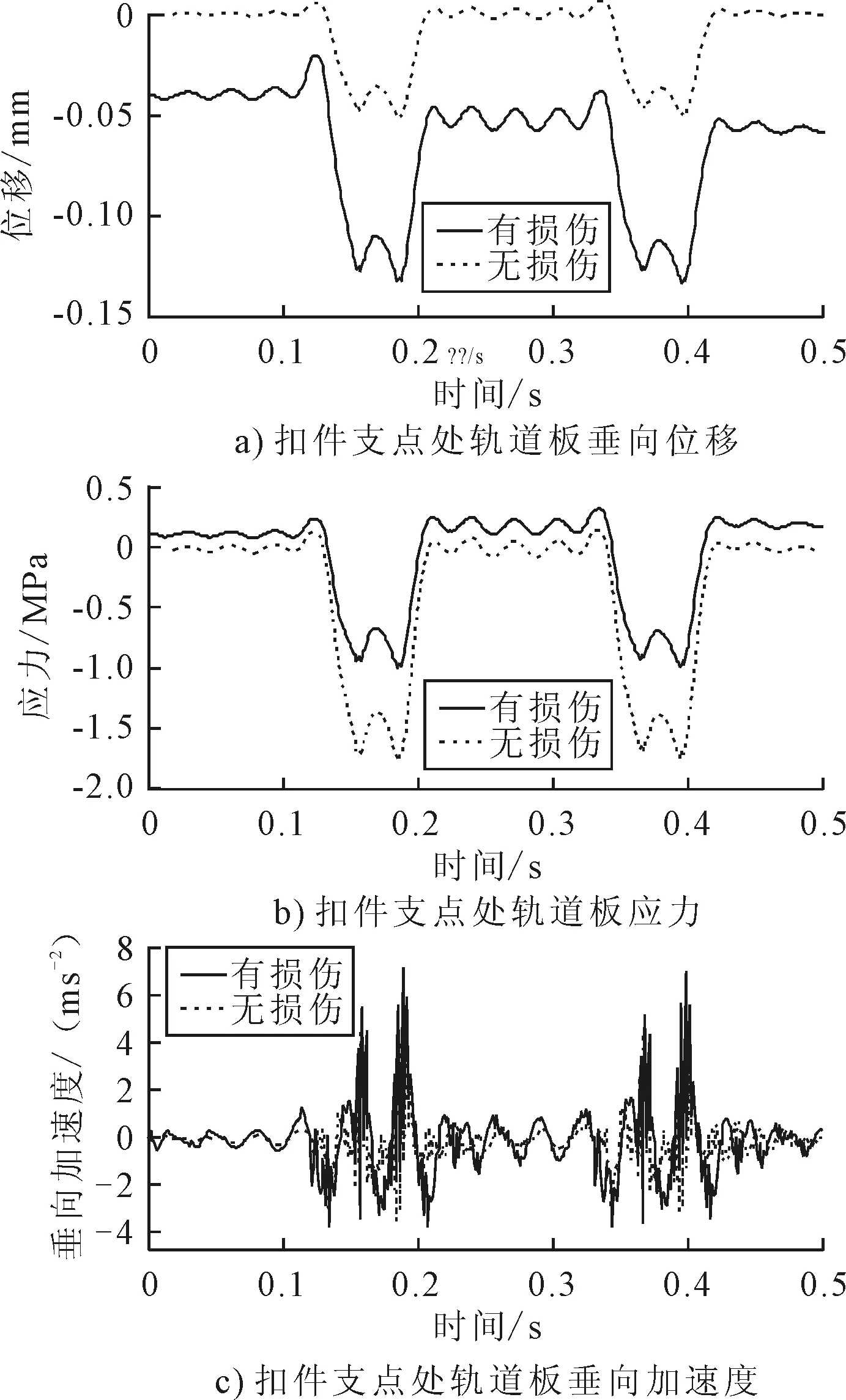
图8 车辆动荷载下CRTSIⅡ轨道板振动响应

由图8a)可知，两种条件下，扣件支点处轨道板垂向位移响应的波形相似，但位移变化幅值差别较大.轨道板无损伤时的垂向位移幅值仅为0.06 mm，有变温损伤后幅值增大到0.12 mm，增幅达100%，说明变温损伤明显削弱了轨道板的抗变形能力.

图8b)对比了车辆通过有、无变温损伤的轨道时，扣件支点处轨道板的动应力响应.车辆通过未受损的轨道时，支点处最大压应力为1.76 MPa，而车辆通过受损的轨道时，最大压应力为1.0 MPa，这是因为轨道板在受损后处于刚度退化状态，混凝土材料进入软化阶段，故轨道板应力幅值减小.

由图8c)可知，车辆通过无损伤和有损伤轨道板时，支点处轨道板垂向加速度最大值分别为4.7和7.3 m/s2，后者较前者增大55%.轨道板受损后，车辆荷载作用下轨道板的振动响应将显著增大，这对无砟轨道结构可靠性和耐久性以及高速列车行车安全性均会造成不利影响.

5 结 论

采用混凝土损伤塑性本构模型，建立了CRTS Ⅲ型板式无砟轨道损伤分析模型，开展了24 h温变作用下CRTS Ⅲ型轨道板的损伤行为分析，并在此基础上，分析了温度荷载和车辆载荷共同作用下轨道板的损伤演化及其对无砟轨道结构动力响应的影响，得到以下结论.

1) 在本文所述温变荷载作用下，当持续降温4 h后，轨道板上表面降温达5.1 ℃，上表面中心处拉应力超过C60混凝土拉伸极限，轨道板开始出现损伤；随着温度继续下降，轨道板应力特性呈现软化下降趋势，应力逐渐减小，但变形继续增大，在破坏最严重的地方，损伤因子和刚度退化系数均由零迅速增加至0.4左右；变温作用17 h以后，温度逐步回升，在轨道板损伤最严重的地方，其损伤值保持在0.44的水平，但刚度退化系数逐渐减小至零，轨道板在变温过程中没有产生压缩损伤.

2) 当轨道板处于降温过程中的最大损伤状态时，施加车辆动荷载作用，计算结果表明：在车辆通过以后，扣件支点处轨道板的刚度退化系数仅有微小变化，说明在不考虑其他影响因素时，变温作用是轨道板产生损伤的主要根源，而车辆荷载并不会加剧轨道板的损伤.

3) 对比分析车辆通过无损伤和有损伤无砟轨道时轨道板的动力学响应，结果表明：相较于无损伤的轨道板，由于受损轨道板混凝土材料进入软化阶段，扣件支点处的压应力幅值有明显减小，但受损轨道板的垂向振动位移幅值增大了100%，垂向振动加速度幅值增大了55%.这说明轨道板在经历变温损伤以后处于刚度退化状态，其抗变形能力被削弱，车辆通过时轨道板振动明显加剧.