实代数中有关正锥的讨论①
2018-12-27,
,
(1.淮北师范大学数学科学学院,安徽 淮北 235000;2.宿州学院,安徽 宿州 234000)
0 引 言
在给定的线性空间中,引进了一个正锥来规定一种序关系。在文中第一节将给出一些定义,第二节证明线性序域(F,<)上的一给定正锥和对于一切属于F的正锥有F中元素的平方和的集合都属于正锥及在正锥P下定义证明F上的一个二元关系为线性序的一关系等。
1 准备工作
定义1[1]称(F,<)为线性序域,假如
1)F为域;
2)″<″是F上的一个线性序;
3)a 定义2[1]称P⊆F是域F上的一个正锥,假如 1)0⊆P,-1∉P; 2)x,y∈P→x+y∈P,xy∈P; 3)∀x(x∈P∨-x∈P). 定义3[1]称域F是可序化的,如果存在F的一个线性序<使得(F,<)为线性序域. 定义4[1]如果F的子集P满足正锥条件的一部分:-1∉P,且对于一切x,y∈P,有x+y∈P,x·y∈P,则P称作F的一个准正锥. 定义5[2]域F中元素之间的一个二元关系称作F的一个序,如果下列条件成立: (1)对于任意a∈F,aa; (2)若ab且ba,则a=b; (3)若ab且bc,则ac; (4)对于任意a,b∈F,ab或者ba; (5)若ab,则对与任意c∈F,a+cb+c; 定理1 假如(F,<)为线性序域,则P={x∈F:x≥0}为一正锥. 证明由P={x∈F:x≥0},即P⊆F. 1)0∈P,-1∉P. 2)任意P中的元素都在F中,现在只需证明P在加法和乘法的运算下是封闭的. 设a,b∈P,a,b≥0 (1)在加法下是显然的. 设a,b∈P,a,b≥0 a+b>0,则a+b∈P. (2)在乘法下: a·b≥0,则a·b∈P. 3)∀x∈F (1)当x>0时,x∈P, (2)当x<0时,-x>0,则-x∈P, (3)当x=0时,x∈P. 定理2 对于F的一切正锥P,∑F2⊆P. 定理3 假如P⊆F为F的一个正锥.定义F上的一个二元关系 x< 可以证明<<为F上的一个线性序关系. 证明1)∀x(x< 2)∀x,yx-y∈Py< y-x∈Px< 即∀x,y(x< 3)∀x,y,zy-x∈Px< z-y∈Py< 即∀x,y,z(x< 4)∀x,y,x-y∈Py< y-x∈Px< 即∀x,y(x< 5)若x< 6)若0< 定理4 证明在准正锥的类ε={P⊇∑F2:P是F的一个准正锥}中⊆是在它上面的一个序关系. 证明证明⊆是准正锥的类的一个序关系,只需证明 x2⊆y2当且仅当y2-x2⊆P (1)∀x,x2⊆x2. (2)∀x2,y2,x2-y2∈Py2⊆x2 y2-x2∈Px2⊆y2 x2=y2∈P 即∀x2,y2(x2⊆y2∨y2⊆x2∨x2=y2) (3)∀x2,y2,z2,y2-x2∈Px2⊆y2 z2-y2∈Py2⊆z2 则z2-x2∈P⟹x2⊆z2 即∀x2,y2,z2(x2⊆y2∧y2⊆z2→x2⊆z2). 因此,通过在实代数中有关正锥的讨论,可以得到在给定的线性序域上有关正锥的证明及正锥的可序化.2 主要结果的证明
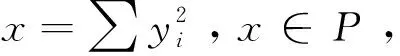

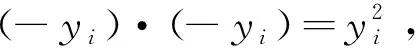
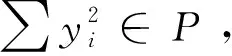
3 结 语
