云计算对于完工时间最小化问题的算法研究①

(滁州职业技术学院,安徽 滁州 239000)

0 引 言

对于云计算服务问题的研究，众多学者从各个方面提出了对应的解决方法，实现云计算服务的效益的最大化。吴小红、王翠娥等人(2012)针对于响应时间提高这一指标，提出了DSIC机制来确保在最短的时间内显示资源成本信息，使得达到响应时间最小化的目标[1]。杨柳、唐卓等人(2012)对响应时间与成本消耗进行了综合考虑，在随机规划理论的基础上提出了虚拟分配的优化算法，实现资源的有效调度与分配[2]。景维鹏，邢乐乐等人(2013)同样采用时间与费用的双重约束条件，提出了一种改进的作业调度算法来缩短响应的时间[3]。从现有的研究上来看，都提出了改良算法，主要是从时间响应上来进行约束。但是却很少从路由传输这一角度出发考虑来减少时间响应。

1 系统模型建立

数据中心与链路集合共同组成了网络图，对此假设这三个集合分别为V={D1,D2,…,Dβ}、链路E与G=(V,E)。数据中心的服务器并不是单一存在的，假设服务器共计有γ个，则可记为={s1,s2,…,sγ}。每个服务器都是γ×β二元矩阵，可用其中：

(1)

Du与Dv之间的传输的链路(u,v)的延时假设为luv，那么链路集合则为β×β的矩阵，可用ML表示，表达式如下(2)所示[4]。

ML={luv},∀(u,v)∈E

(2)

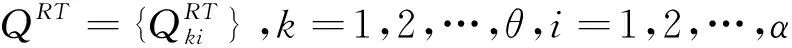
2 问题模型构建

2.1 任务映射

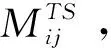
(3)

该约束条件指出每一个任务都需要与服务器连接，也就是说任务必须有服务器处理，则：

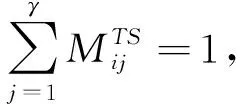
(4)

对于资源容量的约束来说，所分配的任务资源需求容量不能超过服务器所能提供的总容量，故此有如下的条件(5)：

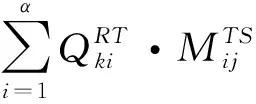
(5)

在计算时间上，其实际时间ei与任务规模Ti呈正相关，对此得到约束条件(6)，其中P0为处理速度。

(6)

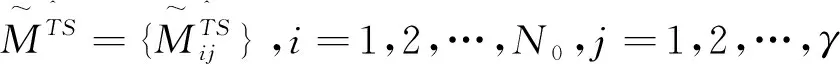
(7)

满足通用性原理，任务是通过随机方式来实现公正分配，假设φ(j)为sj服务器上对接收任务的计算时间，那么我们可以得到(8)

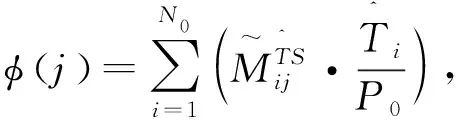
(8)

那么，服务器sj映射下一个任务时所需要的最大的等待时间可以如下表示：

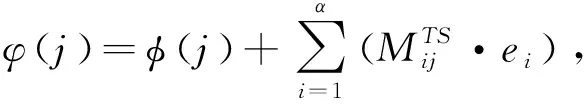
(9)

因此，服务器上的新任务Ti的预期最长周转时间ωi可表示为：

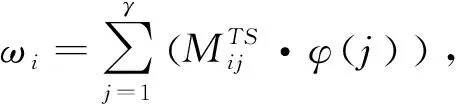
(10)

2.2 任务路由传输

任务路由传输，首先是要确定链路是否起到任务传输的作用，可以通过引入(u,v)∈来进行确认，如(11)所示[5]：

(11)

对于任务分配来说，其分配的服务器并不是与当前的数据中心是对应的，但是一般来说为减少时间与消耗成本常采用同一数据中心的链路，对此可以得到(12)。

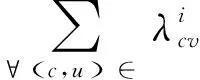
(12)

通过服务器的映射矩阵MTS可以得到一个α×β矩阵MTD,MTD=MTS×MSD，该矩阵反映了映射关系。对于每一个任务来说，其传输必须拥有一条传输链路，中间的数据中心需要保持数据流量的均衡性，综合考虑可以用以下(13)关系式来表达。

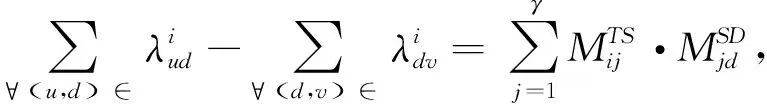
(13)

此外，每条链路上所有任务的总流量必须在其容量范围内，即：

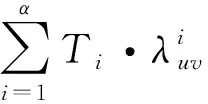
(14)

根据每一个任务的传输延时可以得到总任务量的传输延时的大小γi，即路由器传输的延时，具体如下(15)所示：

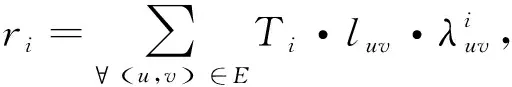
(15)

考虑到云计算最重要的考核指标，任务器传输延时与传输任务的等待时间不应该超过其时间限制ç，对此可以得到以下约束关系式：

ωi+γiζ,∀i=1,2,…,α

(16)

2.3 IPQC问题

根据前面所提到的约束条件，可以将上述的建模简化为一个IPQC问题，即具有二次约束的整数规划问题，如(17)：

(17)

在这些约束中，式(5)和(13)是二次约束条件。IPQC问题属于NP难题，其主要解决的办法包括分解算法、割平面法以及外逼近法等等，但是这些算法运用只适合于特定的IPQC，并且在算法上存在计算冗杂，计算时间长等问题，目前没有一个有效的通用算法来进行解决。为决绝IPQC问题最有效的途径就是将其线性化，采用增加变量与约束条件的方式将函数问题转化为线性函数，从而极大地简化问题[6]。对此提出了启发式算法，其算法在后面详细介绍。

3 启发式算法设计

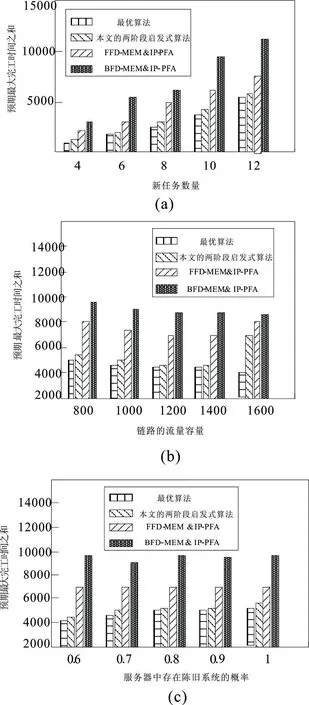
图1 小规模网络环境下三种算法的完工时间性能比较

算法1: 最优拟合递增型任务映射算法

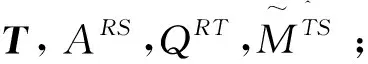
输出：新任务的映射矩阵MTS

1：MTS←{0}

2：T′←根据任务规模对所有新的任务进行递增排序

3：S′←根据服务器寄存的任务数量对所有服务器递增排序

4：for 所有Ti∈T′,∀i=1,2,…,αdo

金沙江区域内地质构造复杂，生态环境脆弱。为此，项目施工过程中，在作业场地设置了沉淀池，废水经过沉淀后用于洒水抑尘，不外排；对临时施工场地以及运输道路定期洒水，减少地面扬尘；做好水土保持工作，最大限度保护好当地生态环境，并在工程结束后进行植被恢复；严格控制炸礁、疏浚作业范围，并在鱼类繁殖季节不进行施工，同时建立鱼类临时救护机制，若发现珍稀保护鱼类，项目部在渔政部门指导下进行救护，通过增殖放流，恢复鱼类资源。

5：for 所有sj∈S′,∀j=1,2,…,γdo

6：ifsj可满足Ti的资源要求 then

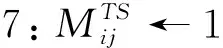
8S′←根据寄存的任务数量对所有服务器再次递增排序

9：break

10：end if

11：end for

12：end for

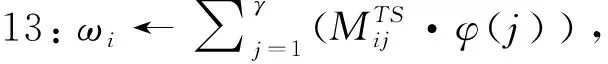
首先对其进行初始化，再根据任务的规模进行排序与存储，算法1的复杂度的为O(γ·N)，当输入变量后就可以得到映射矩阵。在实际的云计算中，数据任务规模是非常庞大的，因此需要寻找最短的传输路径来减少时间等待与传输延时效应。对此最短路径的寻找可以利用基于整数规划的算法2来完成。将前面的映射结果作为输入的变量，在最终结果中就可以得到最优的传输路径。

算法2: 基于IP的路径寻找算法

输入：网络图，任务集合及任务映射算法提供的

1：MTD←MTS×MSD

4 性能评估

4.1 小规模网络的预期最大完工时间

在小规模网络环境下三种算法的完工时间性能比较中，如图1(a)中所示，随着任务量的不断增长，这三种方法的完工时间也同样出现增长的趋势，也就是所完工时间是与任务量的多少成正比的，同时在相同任务量的情况之下启发式算法的完工时间明显要低于其他两种算法。如图1(b)所示，链路容量变化情况下各算法之间的响应时间的发展趋势。当容量从800增长至1600时，两种阶段启发式算法所得到的完工时间呈现不断下降趋势但是下降幅度并不是很大，FFD-MEM与BFD-MEM这两种方法同样呈现递减的趋势，相较而言在容量一定时提出的启发式算法性能更优。如图1(c)所示，随着服务器中新旧任务概率变化时三种算法的完工时间指标变化情况。当新旧任务概率不断增加时，各算法之间的完工时间均在不断增加，造成这样的原因在于概率越大造成任务的等待时间越长从而增加了完工时间。综合不同情况下的三种算法得到的完工时间的长短来看，阶段启发式算法的时间性能明显要优于其他两种算法。

4.2 大规模网络的预期最大完工时间

在大规模网络中路径寻找是关键，对此与最为常用的寻找路径的Dijkstr、 SPFA算法相结合，同样来探寻任务量、流量以及新旧任务这种情况下的完工时间变化，最大完工时间之和与新任务数量间的关系图2所示。其中，图2(a)是IP-PFA的任务映射启发式算法仿真图，图2(b)是Dijk.CAP的任务映射启发式算法仿真图，图2(c)SPFA.CAP的任务映射启发式算法仿真图，图2(d)BFI与最短路径寻找算法相结合仿真图。

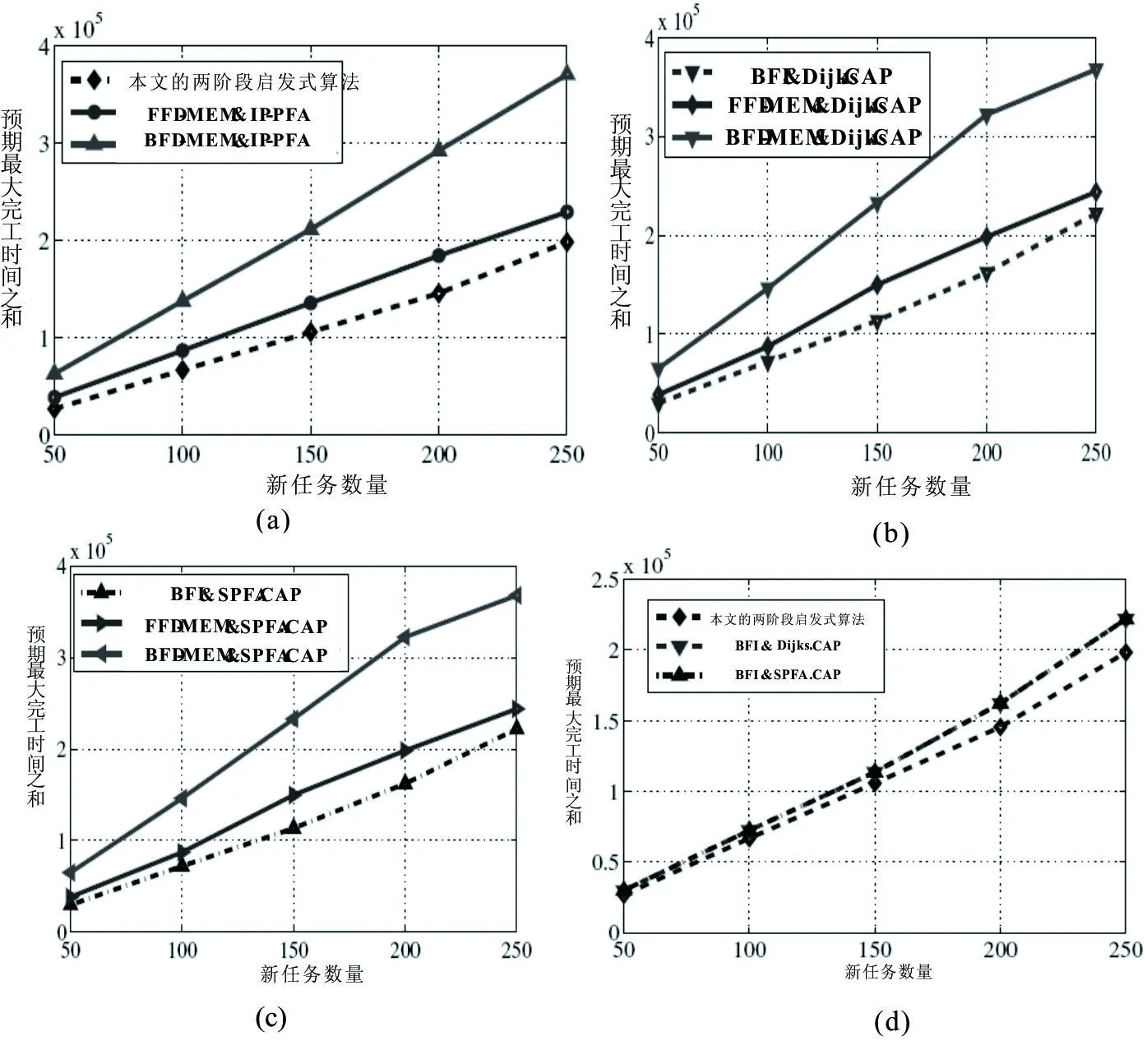
图2 最大完工时间之和与新任务数量间的关系

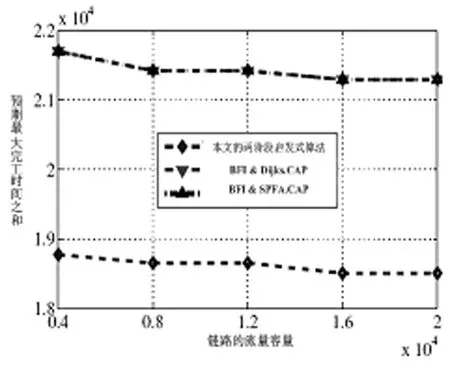
图3 最大完工时间之和与链路容量间的关系

仿真结果如下图3所示。其该三种算法的完工时间的性能变化趋势与小规模网络情况下的相一致。云计算的完工时间会随着任务量以及新旧任务概率的增长而不断增加，会随着链路容量的增加而呈现出递减的趋势。

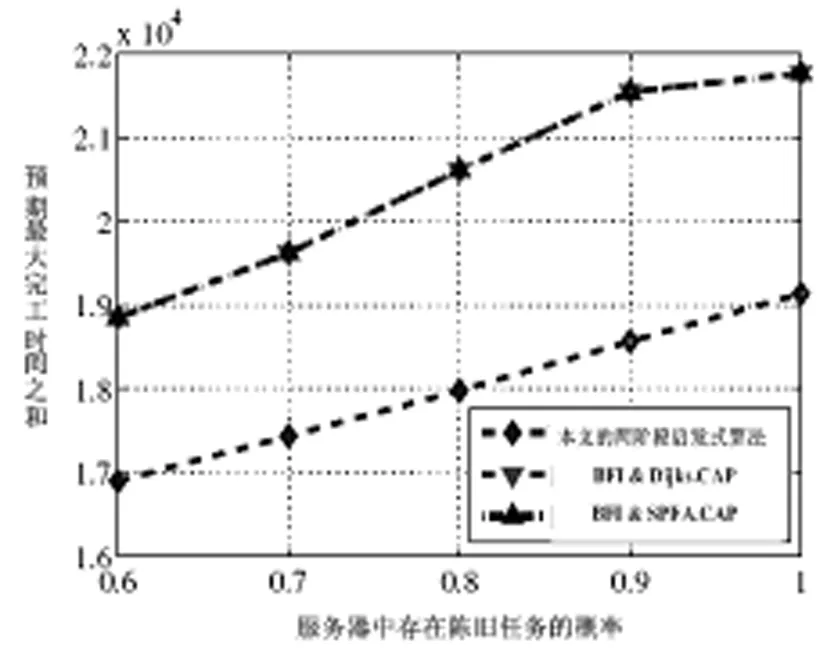
图4 大规模网络环境下三种算法的完工时间性能比较

但综合这三种算法得到的最大响应时间来看，如图4所示。两阶段启发式算法的完工时间最小，性能是最优的， 也就说该算法达到了性能优化的目的。

5 结 论

研究表明，从任务映射与路由传输两个方面进行综合性考虑来进一步缩小完工时间，达到快速响应的目的。将研究的问题简化成IPQC问题，并提出了一种多项式时间复杂度的启发式算法来进一步对问题实现线性简化。通过全面的仿真实验，证明该算法的效率接近于最优解，效率较高，且性能远优于当前其他请求响应算法，证明了两阶段启发算法在云计算中的有效性。