基于小波阈值的图像信号去噪方法研究①

,

(安庆职业技术学院，安徽 安庆 246003)

0 引 言

现实生活中，人们接触、采集到的图像信号很容易受到环境、采集仪器的干扰，利用相机拍摄图像时，会受到光电子噪声的干扰；在图像传输过程中，会受到传输环境以及传输信道的噪声影响等[1]。噪声会减弱信号本身的特征，给信号检测、特征提取带来一系列困难。当前，对图像信号去噪，相关方法有很多。除均值滤波、中值滤波、频域滤波[2]等经典方法外，基于短时傅里叶变换[3]、高阶累积量[4]和经验模态分解[5]的去噪方法均得到了广泛应用。众多去噪方法中，小波阈值去噪能够在对信号进行多尺度观察的基础上，较好的区分噪声与期望信号，并对噪声加以抑制，算法复杂度低，对信号的局部特性损失较小，因此在实际中得到了广泛应用。

1 小波分析理论模型

19世纪，法国科学家傅里叶在解决热传导问题时，总结得到了傅里叶变换公式：

(1)

傅里叶变换能表征信号频域特性，但得到的频域表示不具有时间分辨力，为此， Gabor在1946年提出加窗傅里叶变换的思想，采用固定窗对傅里叶变换进行了改进，但窗函数与ω无关，窗函数给定，信号分析的时间和频率分辨力就给定了。现实中，往往希望在高频段的时间分辨力高一些，低频段的频率分辨力高一些。基于此需要，学者提出了小波变换理论。

小波变换是傅里叶变换、加窗傅里叶变换的一种拓展和延伸，它能够生成一系列的标准正交基，使信号在该基下的分解具有良好时频局部特性。这组基满足以下“容许”条件[6]：

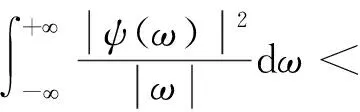
(2)

满足上式的ψ(t)称为基本小波或小波母函数，该母函数相当于是对加窗傅里叶变换的窗函数进行了改进。实际中利用小波基进行信号分析时，会使用伸缩因子a和平移因子b，来保证小波基函数对频域、时域的遍历程度。由此，可以得到连续小波变换的公式：

WTf(a,b)=〈f(t),ψa,b(t)〉=

(3)

式中，小波函数通过平移因子b，在时域上横向移动，而尺度因子a，则保证了参数在时间维的收缩或拓展，这也对应着频域的收缩或拓展。

利用小波反变换进行信号重构的公式为：

(4)

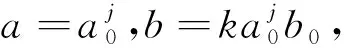
(5)

当a0=2,b0=1时，离散小波基就构成了目前使用广泛地二进离散小波变换。

2 小波阈值去噪原理

利用小波变换去噪，本质上是要找到期望信号与噪声在小波域的可分离性。实际含噪信号中，期望信号的小波系数，在小波域内分布相对集中且幅值较大；但噪声信号分布在全小波域，即在小波域内分布分散且幅值较小。因此，设定阈值，对小波系数幅值大于该阈值的信号予以保留，小于该阈值的予以去除，即可有效去除噪声。其中，去除噪声主要通过小波系数置零的方式实现，小波系数重新调整后，再通过小波反变换实现信号的复原。由此，可以得出小波去噪的基本过程：

(1) 利用合适的小波基函数并确定小波分解的具体层数m，对原始信号f(t)进行m层小波分解；

(2)提取各层小波系数，确定阈值，依据选取阈值及小波系数调整规则对小波系数进行重新调整；

(3)用调整后的小波系数对信号进行重构，即完成了小波阈值去噪的过程。

小波阈值去噪过程中，阈值函数选取及阈值估计比较关键。目前，小波阈值函数选取方式有两种，即硬阈值和软阈值，两种阈值可分别表示为[7]：

1)硬阈值：

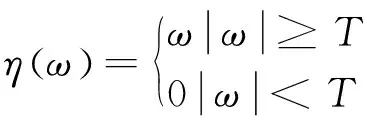
(6)

2)软阈值：

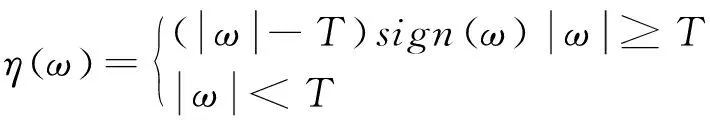
(7)

两种方法各有优劣，硬阈值法操作简单，但会造成在|ω|=T点时，η(ω)的不连续，影响信号重构质量；软阈值很好解决了重构信号不连续的问题，但|ω|≥T时，η(ω)与ω之间有恒定的偏差。实际中，可根据应用场景进行灵活选择。阈值估计，也就是确定式(6)-(7)中的T值。现阶段，阈值选取往往依赖噪声方差σ和信号长度N，实际过程中，通过小波变换，也能够对信号的噪声方差进行很好地估计。噪声与期望信号的混合信号中，噪声主要集中在高频部分，可以通过一层小波变换进行σ的估计，估计的大概流程：

①对信号f(t)进行小波分解：

(8)

②求取第一层小波分解的能量和，即：

(9)

③由此可得到噪声方差估计如下：

(10)

图1 Lena及其含噪图像

3 图像信号去噪模型

图像信号去噪原理与一维信号一致，但图像是一维信号的拓展与延伸，利用小波阈值进行图像去噪，首先要将图像进行离散化，然后估计出图像中的噪声电平，才能利用小波阈值进行图像去噪。

(1)图像灰度离散化：对信号进行数字化处理的第一步是对信号进行离散化，对图像信号来说，往往通过灰度值来对图像信号进行离散化，取图像中颜色最浅和最深的两个值，在这两值之间用一定的量化的位数来表征不同的颜色深度，如256位量化，这是把整幅图像的颜色区分成256个量级，每幅像素都对应有一个量级，这样就用灰度值实现了图像信号的离散化。

(2)图像中的噪声水平估计：设zi表示第i幅图像对应的灰度值，p(zi),i=1,2,...,L，是对应的概率直方图，其中L为对应的量化位数，利用下式求取该直方图的各阶中心矩：

(11)

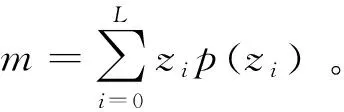
图2 图像信号的db3小波分解结果

图3 小波分析工具箱中图像信号阈值去噪的相关界面

图4 小波阈值去噪后的图像信号

实际统计时，图像噪声的方差可通过图像中某平滑部分的直方图获取，即选取某平滑部分图像，利用式(11)计算其二阶中心矩，即可得到图像噪声方差的估计。

由此，可给出利用小波阈值方法去除图像噪声的详细流程，即图像灰度离散化—图像的小波变换——图像噪声方差估计——阈值求取与设定——阈值函数选取——根据选取阈值调整小波系数——图像信号重构。

图像处理领域常采用去噪后的峰值信噪比(PSNR)衡量去噪算法的去噪效果，设图像长度、宽度分别是M和N，灰度级为L，两指标计算公式为：

(12)

4 图像信号去噪方法仿真

选用经典的Lena及其含噪图像进行去噪效果仿真，原始图像、含噪信号如图1。

利用Matlab小波分析工具箱,选用db3小波对图像进行分解与重构，分解及重构结果如图2所示。图2(a)、(b)两幅图像中，左上角都表示原始图像，左下角都表示重构图像，右下角都表示分解后的图像。

通过图2能够看出，通过db3小波分解，图像信号能够被分解到多个层次，且分解层次越高，图像信号被分解的越精细。以图a为例，分解后的4幅图像中，左上角的图像显示的是原图像的低频信息，右下角的图像显示的是高频信息。通过分解图可见，低频图像显示了原图的概貌信息，而高品图像则显示了原图的细节信息。同时，通过图2，还能够发现小波分解后，图像信号还能够被很好的重构，及图像信号的原始特性在分解过程中并没有受到破坏。

再利用工具箱对含噪信号进行处理，小波分析工具箱进行去噪处理的工作界面如图3所示。从工作界面中，能够直观的观察到灰度直方图及噪声水平的估计过程。

分别利用软、硬阈值去噪方法进行去噪，得到去噪后的图像如图4所示。

利用式(12)计算去噪后的输出峰值信噪比，得到软阈值去噪后的峰值信噪比为81.7db，而硬阈值去噪后的峰值信噪比为83.6db。由此看出软硬阈值去噪均能够有效减轻图像受干扰程度，提升图像质量，软阈值去噪后，图像会有一定的噪声残留，但去噪后图像较“平滑”，即图像连续性得到了很好的保持；硬阈值去噪后噪声残留少，但图像连续性变差。再利用均值滤波、中值滤波和频域去噪对含噪图像进行去噪处理，得到图像处理效果如图5所示。

计算各方法去噪后的输出峰值信噪比，结果如表1所示。

表1 不同去噪方法下的图像输出峰值信噪比

通过图5和表1，能够得出以下结论：

(1)几种去噪方法均能够有效的滤除噪声，获得较高的输出峰值信噪比。

(2)小波阈值去噪，能够获得较其他去噪方法更好的去噪性能，两种小波阈值去噪方法中，软阈值小波去噪很好的保持了图像的连续性，但有一定的噪声残留；而硬阈值去噪有较高的输出峰值信噪比，但图像的连续性较差。

5 结 语

小波分析理论可对信号进行多层分解，能够提取信号在各时、频维度的能量信息，为混合信号的分离、滤波等提供有效手段。利用小波分析进行图像信号的分解与重构，通过设定阈值的方法，实现期望信号与噪声信号的分离，并通过小波系数置零，实现图像信号的去噪。仿真结果表明，小波阈值去噪方法能很好的滤除噪声信号，且去噪性能较其他传统去噪方法具有更好的去噪性能。