基于kalman滤波的智能小车GPS轨迹跟踪①
2018-12-27
(1.中国科学技术大学信息学院,安徽 合肥 230026 2.安徽财贸职业学院 云桂信息学院,安徽 合肥 230601)
0 引 言
全球定位系统(GPS)是一种全天候空间基准的导航系统,可满足位于全球任何地方精确三位导航与定位的新一代导航和定位系统,有着广泛的应用领域。智能小车GPS轨迹跟踪是将GPS接收机安装在运动目标(智能小车)上就可以进行导航跟踪和定位。通过GPS接收机实时接收在轨导航卫星播发的信号,算出接受载体(智能小车)的位置和速度。对于民用领域GPS的时钟信号认为加入了高频振荡随机干扰信号,该干扰信号可看作GPS定位的观测噪声,致使所有派生的卫星信号均产生高频的抖动[1]。为提高智能小车的GPS轨迹跟踪精度,采用了卡尔曼滤波器对智能小车GPS轨迹跟踪速度以及位置的观测信号进行最优状态估计。
1 卡尔曼滤波(The Kalman Filter Algorithm)
kalman滤波是一种利用线性系统状态方程,是通过系统输入输出观测数据,对系统状态进行最优估计的算法[2~3],由于观测数据中包括系统中的噪声和干扰的影响,其最优估计可看作为滤波过程[4],其线性随机微分方程描述如下:
x(k)=Ax(k-1)+B(u(k)+w(k))Z(k)=
Hx(k)+v(k)
上式中,x(k)、z(k)、u(k)分别为k时刻的系统状态、测量值和k时刻对系统的控制量[5],A、B为系统参数,H为测量系统参数,对于多模型系统和测量系统,A、B、H均为矩阵[6],w(k) 、v(k)分别为过程控制干扰噪声和测量噪声,对于线性随机微分系统,测量和过程都是高斯白噪声(White Gaussian Noise),它们的covariance 分别为Q和R。采用系统的过程模型来预测下一状态的系统。现假设系统的状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在的状态[7]:
x(k|k-1)=Ax(k-1|k-1)+Bu(k)
(1)
(1)式中x(k|k-1)是利用上一状态预测结果,x(k-1|k-1)是上一状态最优结果,u(k)为现在状态的控制量,现在系统结果已经更新了,但对应于x(k|k-1)的covariance还没更新,用p表示covariance:
p(k|k-1)=Ap(k-1|k-1)A′+Q
(2)
(2) 式中Q是系统过程的covariance,p(k|k-1)和p(k-1|k-1)分别是x(k|k-1)和x(k-1|k-1)对应的covariance,A′表示A的转置矩阵。式(1),(2)是对系统的预测,有了当前状态的预测值,再收集当前状态的测量值,结合测量值和预测值,就可得到当前状态(k)的最优化估算值x(k|k):
x(k|k)=x(k|k-1)+Kg(k) (z(k)-Hx(k|k-1))
(3)
其中Kg为Kalman增益( Gain):
Kg(k)=P(k|k-1)H,/ (HP(k|k-1)H,+R)
(4)
为了使Kalman滤波器能不断地运行下去,直至系统过程结束,就要不断更新k状态下x(k|k)的covariance:
p(k|k)=(I-Kg(k)H)P(k|k-1)
(5)
(5)式中I为1的矩阵,当系统进入k+1状态时,P(k|k)就是式子(2)的P(k-1|k-1)。这样,算法就可以自回归的运算下去。根据公式(1)、(2)、(3)、(4)、(5),通过matlab软件编写程序实现正弦信号rk=sin(2*pi*0.1/100.*(0∶N-1))在干扰信号noise=(rand(1,N)-0.5)*R^0.5下的滤波效果如图1、图2所示。对比图1、图2可见经过kalman滤波后波形更加真实。
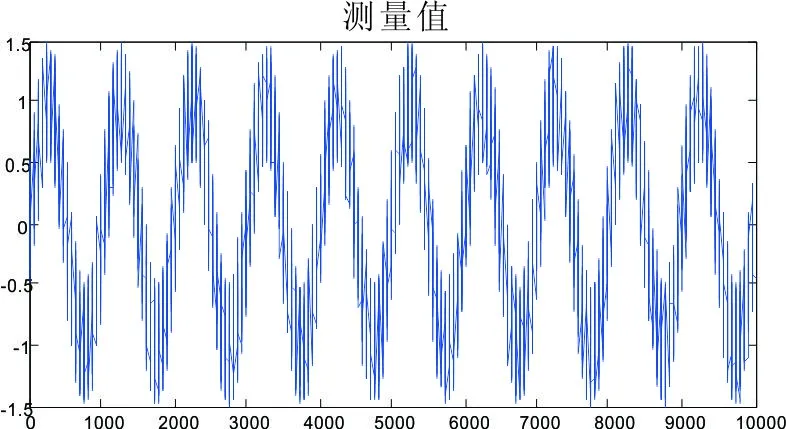
图1 滤波前

图2 滤波后
2 智能小车GPS导航定位
2.1 智能车导航原理如图3所示:
已知目标经纬度(x2,y2)和无人车经纬度(x1,y1),两点间距离至N极夹角为
而车辆通过获取磁传感器数据,也会有一个与N极的夹角β,即车头与N极夹角。通过计算二者角度差θ=β-α,从而计算出控制转向舵机应该输出的角度。
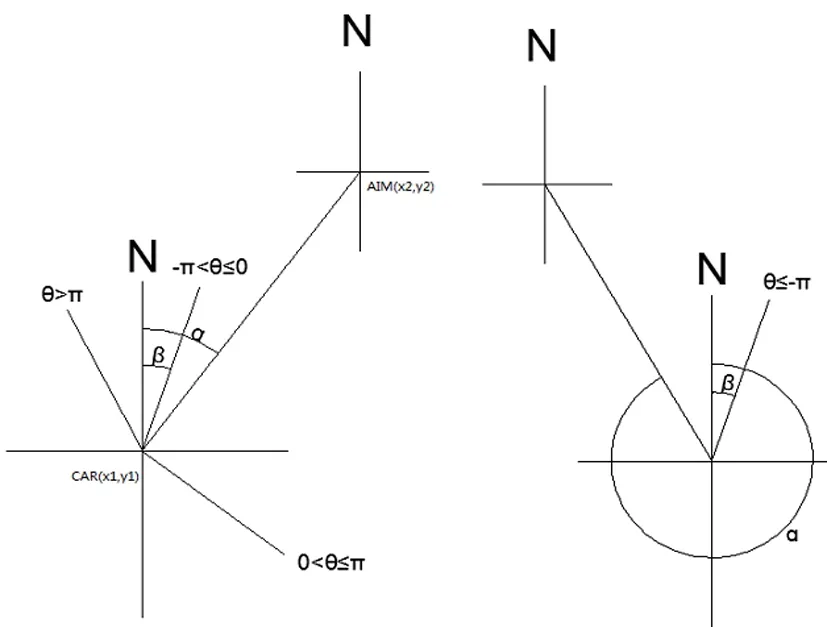
图3 导航原理图
这其中应该有四种可能。如图3-1,当θ>π时,车头在N极左侧,目标位置在N极右侧,车轮应该右转|π-θ|。
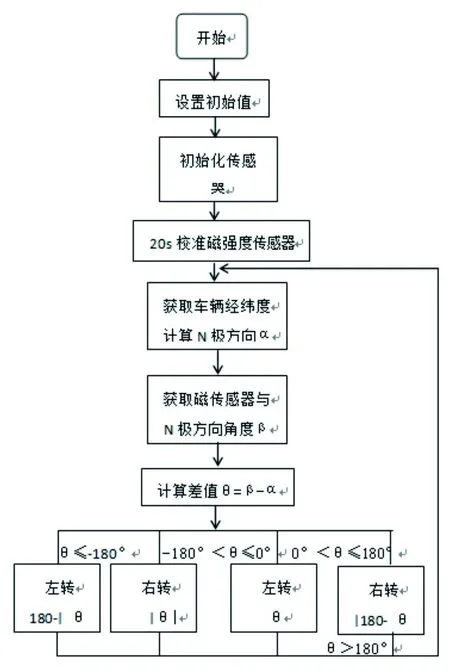
当0<θπ时,车头和目标位置都在N极右侧,车头与N极夹角更大,这时车轮应该左转θ。
当-π<θ0时,车头和目标位置都在N极右侧,目标位置与N极夹角更大,这时车轮应该右转|θ|。
如图3-2,当θ-π时,车头在N极右侧,目标位置在N极左侧,这时车轮应该左转π-|θ|。程序流程图如下:
2.2 GPS是一种利用时间测距的定位系统
其定位的基本原理如图4所示:
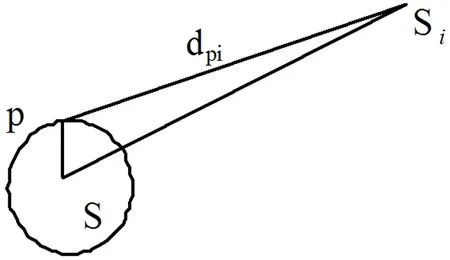
图4 卫星与物体几何关系
如图4所示,设物体所在点P到卫星Si的距离为dpi,如卫星时钟与接收机时钟完全同步,则有如下方程:
dpi=C(tpr-tsv)-CτA
(6)
式中C为光速,tpr为地面接收机同步观测的时刻,tsv为卫星Si同步发射的时刻,τA为传播过程中的附加延时。因为在传播过程中卫星时钟和接收机在实际应用中不能达到完全同步,所以,实测距离并非实际距离,称为伪距[8],记为ρpi,并且有:
ρpi=C(tpri-tsvi)
(7)
式中:tpri、tsvi分别为含钟差的地面物体接收机的观测时刻和含钟差的卫星Si的发射时刻, 其中:
tpri=tpr+δtpri
(8)
tsvi=tsv+δtsvi
(9)
式中:δtprit、δtsvi-分别是地面接收机的钟差和卫星si发射时刻的钟差,
则有:
ρpi=C(tpr-tsv)+C(δtpri-δtsvi)=
dpi+CτA+C(δtpri-δtsvi)=dpi+dpi
(10)
式中:δdpi为测距误差。
另一方面,接收机可通过卫星星历计算出Si点的坐标(Xsi,Ysi,Zsi),这里,设用户位置p点的坐标为(Xp,Yp,Zp),则有:
(11)
将式(11 )代入式(10)
+δdpi
(12)
其中,Xp,Yp,Zp和δdpi为未知数,因此,若同时观测到4颗不同卫星到P点的伪距值ρpi(i=1,2,3,4),根据式( 2-7 )导出的四个方程联立成方程组,即可求出各未知数,从而求出P点的坐标(Xp,Yp,Zp)。
3 状态方程建立
为了简化模型,假定智能小车GPS沿直线方向运动,设采样时间为T0, GPS在采样时刻处时的真实值用kT0表示,用y(k)表示T0时刻处的GPS观测值,则测量模型描述如下:
y(k)=s(k)+v(k)
(13)
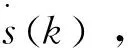
s(k+1)=s(k)+s(k)T0+0.5T02a(k)
a(k)=u(k)+w(k)
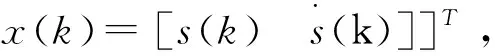
观测方程为:


即系统的状态空间方程为
x(k+1)=Φx(k)+Bu(k)+Гw(k)
y(k)=Hx(k)+v(k)
式中
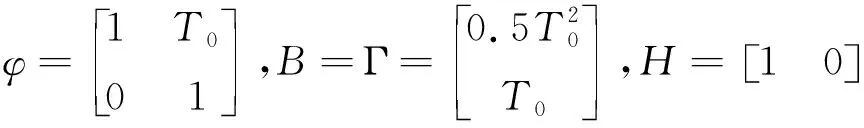
4 仿真结果
设定智能小车在二维水平上运动,初始位置设置为(100m,200m),水平运动速度为2m/s,垂直速度为2m/s,GPS接收机的扫描周期为T=1s,观测噪声的均值为0,方差为100。过程噪声delta_w取值越小,目标越接近匀速直线运动,反之,则越接近于曲线运动[10],在matlab 软件环境下仿真结果如下图5、图6所:
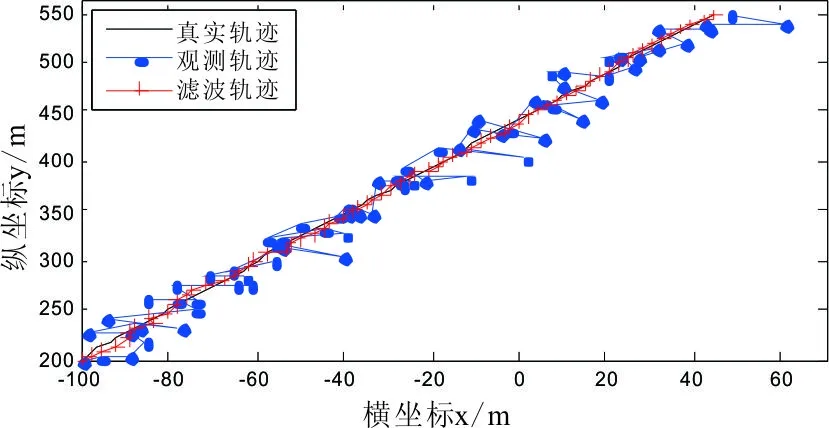
图5 跟踪轨迹图
当过程噪声选取为:delta_w=1e-4,Q= delta_w *diag([0.5,1,0.5,1]),得到跟踪轨迹如图5所示;当过程噪声选取为:delta_w=0.1;,Q= delta_w *diag([0.5,1,0.5,1]),得到跟踪轨迹如图6所示:
当过程噪声选取为:delta_w=1e-4;Q= delta_w *diag([0.5,1,0.5,1])时得到跟踪误差图,如图7所示;当过程噪声选取为:delta_w=0.1;Q= delta_w *diag([0.5,1,0.5,1]) 时得到跟踪误差图,如图8所示。
图5、图6展示了真实轨迹、滤波轨迹与观测轨迹的对比图,红色为滤波轨迹,黑色为真实轨迹,蓝色为GPS 接收机的观测轨迹,可以看出 GPS 接收机接收的信号跳跃性比较大,观测轨迹振荡比较明显,说明测量噪声影响比较大,不能真正的定位,无法真正的反映真实轨迹,且出现漂移现象。对比图5、图6的3条轨迹发现kalman 滤波后的滤波轨迹比较接近目标的真实运动轨迹,能够完成GPS导航的要求。由图7、图8中可以看出位移的观测噪声最大接近25m,噪声相对也是比较大,这仅限于仿真,实际传感器误差不可能这么大。但经过Kalman滤波之后,位置误差值降低到8m以下,可以看出,Kalman滤波虽然不能完全消除智能小车GPS导航中的干扰噪声,但它完全可以最大限度地降低噪声的影响。

图6 跟踪轨迹图
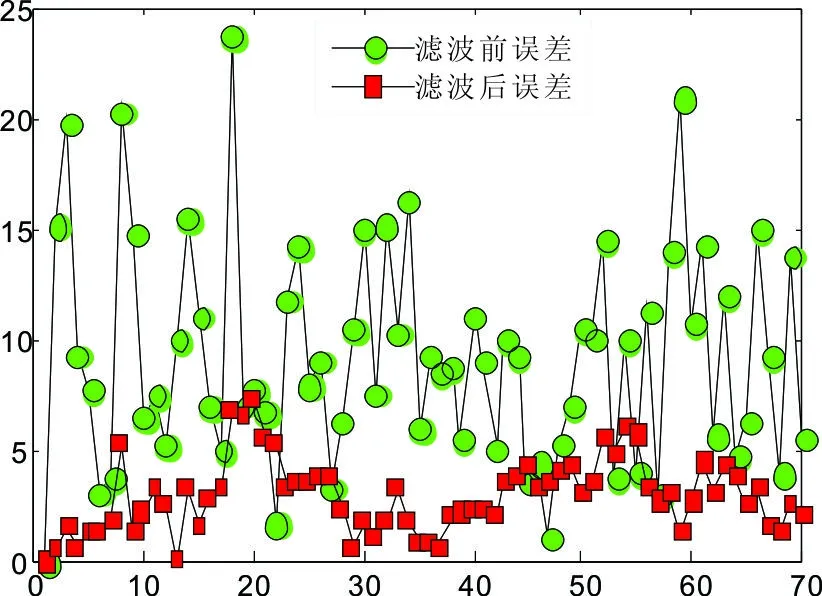
图7 跟踪误差图(delta_w=1e-4;)
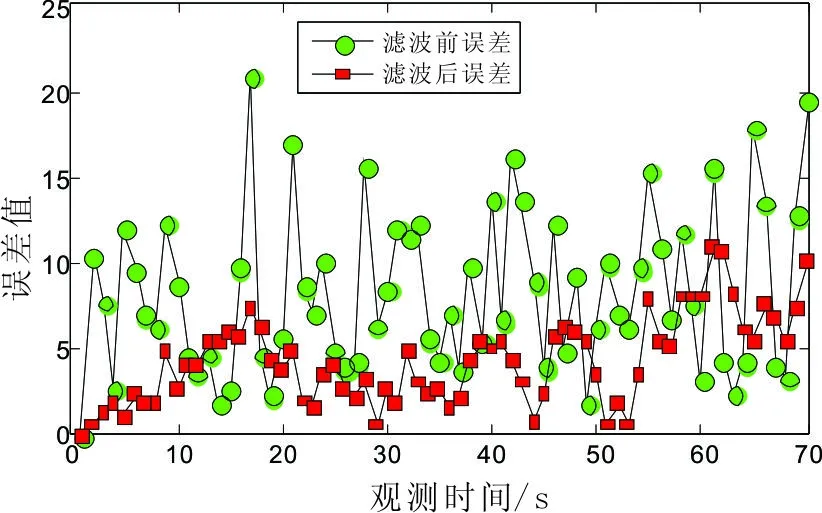
图8 跟踪误差图(delta_w=0.1)
5 结 语
针对基于kalman滤波的智能小车GPS轨迹跟踪进行了研究,分析了kalman滤波、GPS导航定位原理以及Matlab模型的建立,并对其进行了仿真研究,得到以下结论:
1)为了降低智能小车GPS导航定位系统中的干扰信号,采用了离散型Kalman滤波对GPS信号进行了处理,并通过对当前时刻状态结合历史时刻状态进行了下一时刻的最优估计。
2)由于文中GPS的噪声信号属于高斯白噪声且服从正态分布,为了避免在长久意义上走曲线易发生耦合,文中只采用了直线轨迹跟踪,后续研究将对曲线运动的轨迹进行优化。
3)由仿真结果可得Kalman滤波尽管不能完全消除噪声,但已能最大程度的抑制噪声,也极大地提升了智能小车GPS轨迹跟踪的稳定性。
