基于流体力学下潮汐车流收费站的调度研究

2018-12-27范泽华崔雅洪陈茂林

无线互联科技 2018年20期

范泽华，张雷，崔雅洪，陈茂林

（重庆交通大学，重庆 400074）

随着经济和技术发展水平的不断提高，国民人均拥车量也在不断提升。单向拥堵状态是我国普遍存在的问题。在高峰侧的收费站排队时间过长，导致交通拥堵，而低峰侧的收费亭却处于空闲状态。动态调整收费亭的收费朝向是解决单向拥堵的有效途径。目前国内的高速公路收费方式人工半自动收费车道（Manual Toll Collection，MTC）与电子不停车收费系统（Electronic Toll Collection，ETC）均可改变收费朝向[1]。

1 建立车辆通过高速公路收费广场耗时数学模型

国内高速收费广场的设定通常分为进站缓冲区、排队服务区和离站缓冲区3部分，设定车辆通过这3部分区域所耗费的时间分别为Tn，Tw，Tu。得到车辆通行耗时T的模型为T=Tn+Tw+Tu，车辆通行耗时T的模型可以划分成3个子模型，其中从交通流量q0和交通流量v 3个层面建立3个子模型之间联系。

1.1 进站缓冲区耗时模型

假设交通流是自由流，并以初始交通流速v0和初始交通流量q0进入收费广场过渡段，则依据交通流理论有q0=v0k0。任取进站缓冲段的x点处，分别设交通流速和交通流密度为v(x),k(x)，得到两者与流通量q0的关系式为q0=v(x)k(x)。因交通流量在进出消费广场的全程是保持不变的，所以可得交通流密度与过渡段宽度w(x)的关系为k0wn=k(x)w(x)。

综上所述，得到车辆进入过渡段耗时的平均时间Tn的最终表达式为：

1.2 排队服务区的耗时模型

根据交通流在进出站的全段稳定性，从进站缓冲区到离站缓冲区整个过程3个阶段的交通流量近似相等，得到q0=q1=q2。依照流体力学原理，车流量是平均分配到各个收费车道，所以每个收费路口的车流量为q1/n。根据排队论，每个收费路口服从M/M/1系统，则第2阶段的所有收费路口服从M/M/c系统，即多服务台负指数分布排队系统。分别设定车辆的平均到达率与平均服务率为λ,μ，经演算得出车辆在收费站点的排队耗时为：

其中λ=q1/n，得到最终车辆在排队耗时的平均时间Tw为：

1.3 离站缓冲段耗时模型

假设车辆脱离服务阶段后有个起步速度v2、车流量q1，最后以车流量q2汇流进入主线。第3阶段与第1阶段相似，因此省略其推导过程，直接给出车辆离站缓冲段耗时的平均时间Tu的表达式为：

2 基于高低车流量下对收费站的改进

2.1 考虑高低车流量下对问题进行分析

针对轻重车流量问题，本文提出往复变向公用车道（亦称潮汐车道）的新思路。在收费广场收费路口的中间放置潮汐车道。高峰时期在该方向上开放潮汐车道，以缓解交通拥挤的情况。低峰时期可根据实际状况，合理管理潮汐车道，包括每个潮汐车道开关状态和开放的方向[2]。

运用流体力学模拟理论，近似地将高速公路收费广场的交通流看作连续流进行研究。根据公式（1）—（4），有车辆通过高速公路收费广场耗时T的目标函数为：

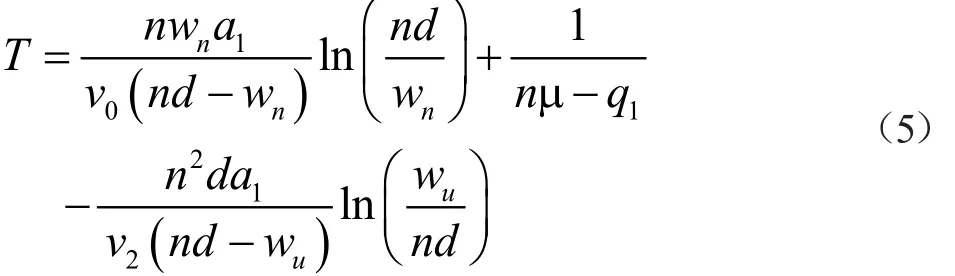
2.2 高低车流量下应设的收费站个数（单方向）

设定高速公路是标准的横断面，单行车道宽度w为3.75 m，双向五车道高速公路主线宽度wn，wu均为18.75 m，单个收费窗口的宽度为5 m。假设收费窗口平均服务率为600 pcu/h，车辆进站的初始速度为40 km/h，脱离收费服务区域的速度为20 km/h。高车流量平均到达率E(q0)1为4393 pcu/h，轻车流量平均到达率E(q0)2为2 227 pcu/h。

其中收费站个数n为模型的主体变量，收费站个数与车辆通过高速公路收费广场的总耗时存在相关性。n的取值受到建造与运营成本的约束，通过变换n值就可以接触通过收费广场3个阶段的时间以及总时间，从而取得总体的最优值。

当车辆的平均到达率为λ小于平均服务率μ，可保证系统的稳定并避免收费广场处于瘫痪状态。其中λ=q1/n，可以得出n的另一约束条件为n＞q0/μ。因此，在n从6到16的过程中，用Matlab求出所对应的每个Tn，Tw，Tu，如表2—3所示。

依据表2可得，当收费站个数n高=10的时候，车辆通过收费广场消耗的总平均时间最少。据表3可得，当收费站个数n低=6的时候，车辆通过收费广场消耗的总平均时间最少。

表2 高车流量下对应每个n的通过收费广场各段的时间和总耗时

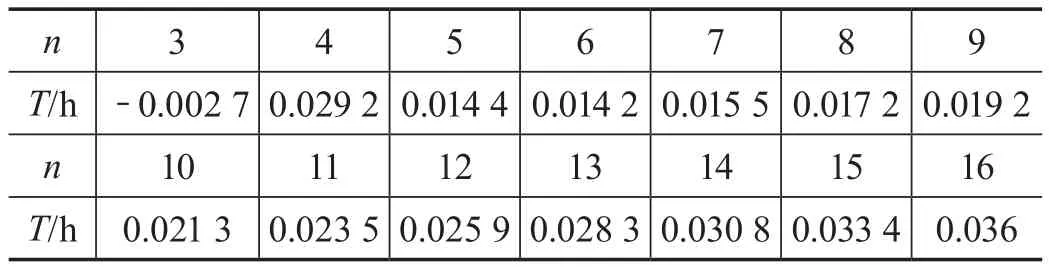
表3 低车流量下对应每个n的通过收费广场各段的时间和总耗时

3 结果分析

通过求解可知，对于收费站个数n=9的收费广场，在高车流量情况下需增加一个收费站方能满足需求，而在低车流量情况下只需6个收费站就可以满足需求。因此，总共需设置16个收费站，为保证两个方向都满足低车流量时所需的6个收费站数，中间应设置4个潮汐车道。两个方向所开的收费车道数的情况如下：（1）当两个方向都是低车流量，两个方向都只开放6个收费车道，中间4个车道关闭，以节约成本。（2）当两个方向都是高车流量或正常流量，两个方向都只开放8个收费车道。（3）当一个方向高车流量时，高车流量方向开放10个车道，对立方向开放6个收费车道。