改进主成分分析的KNN故障检测研究

李 元, 白岩松

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

随着近年来科学技术的快速发展，工业生产过程越来越复杂，其中具有很多生产环节，且各环节间联系更加紧密.现代工业生产过程具有规模大、危险性高、影响因子多等特点，导致其产生的故障具有类型多、相关变量多[1]等特点，因此，保证生产过程安全可靠运行对当今社会活动有着重大的意义.在故障检测过程中，为确保检测结果的准确可靠，通常尽可能多的收集大量数据，获得足够多的信息.

对于实际生产过程，故障检测方法大致可以分为3类[2]：基于数据驱动的方法、基于解析模型的方法和基于知识的方法.由于基于数据驱动的故障检测方法通过研究过程产生的数据进行故障检测，无需建立相应的模型，因此，基于数据驱动的方法越来越受到专家和学者的关注，其中，统计过程控制(Statistics Process Contol,SPC)方法为基于数据驱动的方法中最常用的方法之一[3].SPC即为通过判断当前时刻数据是否处于正常数据周围进行故障检测.从统计方面来说，通常是通过比较当前时刻数据与正常数据的概率密度判断是否发生故障.然而，对于复杂的工业过程，估计其多维空间的概率密度十分困难.

针对上述问题，Q.Peter He提出了一种基于k最近邻规则(k-Nearest Neighbor,kNN)的故障检测算法[4-5]，该方法以样本间的距离为标准衡量样本故障与否，其具有简单、直观、健壮性强等特点，能够处理非线性问题和时变性问题；由于该方法需要对每个待分类样本进行计算以得到k个近邻[2-4]，因此具有计算量大、所需存储空间大的缺点.当生产过程由于生产因素变化产生多个工况时，产生的数据归属于几个不同的工况.对于待检测样本，其边界往往具有不确定性，此时采用kNN算法进行在线检测效果不够理想，容易产生漏报或误报的情况.

本文研究基于主成分分析(Principal Component Analysis,PCA)方法在故障检测领域的应用[6-8]，在分析PCA方法局限性的基础上提出一种新的基于K-means 主成分分析k近邻规则(K-means Principal Component AnalysisK-Nearest Neighbor,K-PCA-KNN)的故障检测方法.K-PCA-KNN方法首先采用k-means算法对原始数据进行聚类处理，然后利用PCA算法降维，减少计算量，最后使用k近邻规则构建距离统计指标进行故障检测.本文最后通过青霉素发酵仿真实验验证所提方法的有效性[5].

1 相关算法介绍

1.1 K-means聚类

K-means聚类算法分别于1995年由Steinhaus、1965年由Ball & Hall、1967年由McQueen各自在不同的研究领域提出[9].聚类算法的主要中心思想即为对收集到的全部数据进行分类，使不同类别数据之间的差距尽可能大，相同类别数据之间的差距尽可能小.该算法与其他分类算法的不同之处在于：在聚类开始前，类别数、分类标准以及聚类分析时数据集合的特征均是未知的.

给定一个数据集X={x1,x2,…,xi,…,xn}∈Rn×d，K-means聚类算法将数据集划分为K个子集C={ck,k=1,2,…,K}，每个子集代表一个类别，每个类存在一个类别中心μk.划分类别时，根据数据对象间的相似程度进行分组，使数据满足如下条件：

{Cj|j=1,2,…,k},Cj⊆V,

(1)

以上过程称为聚类，{ck|k=1,2,…,K}称为簇.

本文选用欧氏距离作为数据间相似性判断准则，使用式(2)计算类内各点到聚类中心μk的距离平方和.

D2(ck)=∑xk∈Ck‖xk-μk‖2

(2)

聚类算法主要包括数学分类学和传统模式识别两部分.其基本实现方法可以为预先定义两个样本间的距离，也可以不依赖距离，预先定义一个优化目标，通过优化获得最小值.

定义聚类算法的输入为待分类样本[x1,x2,…,xm]，其中两个子类中心的最小距离阈值为θ；算法的输出为子类数量c，其中子类中心为[x1,x2,…,xm].

聚类算法的具体流程如下：

(1) 在空间内选定k个数据点作为初始的聚类中心，其中每个点代表一个类别的中心，一般是从样本中均匀选取；

(2) 计算各聚类中心的距离，若距离小于预定的阈值θ，则剔除其中一个聚类中心；

(3) 计算所有样本与聚类中心的距离，以距离为准则将它们分配到与其最近的中心进行聚类.

(4) 经过Inum次迭代后，若某聚类中心所获得的样本数没有达到一定数量，则剔除该类别.当所有样本均分配完成后，重新计算k个聚类中心的位置.

(5) 若结果满足收敛条件则结束计算，反之返回步骤2至满足收敛条件.收敛条件通常为：两次迭代的聚类中心之间的距离变化小于一个很小的数ε，或类内各点到其聚类中心的距离平方和及子类之间的距离平方和达到最小.

1.2 主成分分析(PCA)

对于复杂的现代工业实际生产过程，往往存在很多个变量，每个变量在不同程度上携带着与生产相关的不同信息，且许多变量之间存在一定的相关关系，根据这些变量能够获取信息，以便对问题做出较为可靠的判断.然而过多的变量会导致数据维数过大、计算量大且复杂，进而增加问题分析难度.PCA就是一种提取少数变量，利用其与大多数变量的相关关系反映原有信息的算法，通过对提取的少数变量进行研究达到降维效果.

定义一个(n×m)维的数据矩阵X：

(3)

为消除量纲的影响，由下式对矩阵X进行z-score标准化处理，得到均值为0，方差为1的矩阵X*：

(4)

计算标准化后矩阵X*的协方差矩阵：

(5)

同时，求出S的特征值λi及其对应的特征向量pi，i=1,2,…,m，并按照从大到小的顺序排列.取前A个特征值及其对应的特征向量，得到主元空间的协方差矩阵Λ和负载矩阵P，由式(6)得到主元的得分矩阵T：

T=X*·P

(6)

一般情况下，PCA算法中A的大小通常采用方差贡献率方法(一般要求贡献率达到80 %以上)或经验法确定.

1.3 k近邻(kNN)

kNN算法根据距离衡量样本间的相似程度：距离越大，相似程度越低；距离越小，相似程度越高.其基本思路为：对于测试样本库和训练样本库，求取每个测试样本与训练样本之间的距离，选择距离最近的k个近邻，根据k个近邻所属类别对测试样本进行归类.

常用的距离有欧氏距离、曼哈顿距离和马氏距离等，本文选用欧氏距离，具体计算公式如下：

(10)

其中：dij表示第i个样本与第j个样本之间的距离.

2 青霉素发酵过程仿真研究

2.1 青霉素发酵过程

青霉素是一种极具临床医用价值的抗生素，广泛应用于现代社会.青霉素的生产过程是一个具有时变性、非线性、多阶段等特点的间歇过程.该过程初始为间歇培养过程，此时微生物在培养基中生长，40 h后由发酵过程转换为半间歇操作模态.本文运用的仿真平台为美国Illinois州立理工学院AliCinar领导的过程监控与技术小组设计的青霉素生产仿真软件Pensim 2.0，该软件可以对不同初始条件下青霉素生产过程的不同变量进行仿真，产生所需实验数据.

本文选取分属3个工况的75个正常批次进行仿真实验，每个批次具有17个变量，如表1所示.采样时间为400 h，每1 h采样1次，3个工况反应体积分别设置为130 L、160 L和190 L，每个工况各产生25个批次.

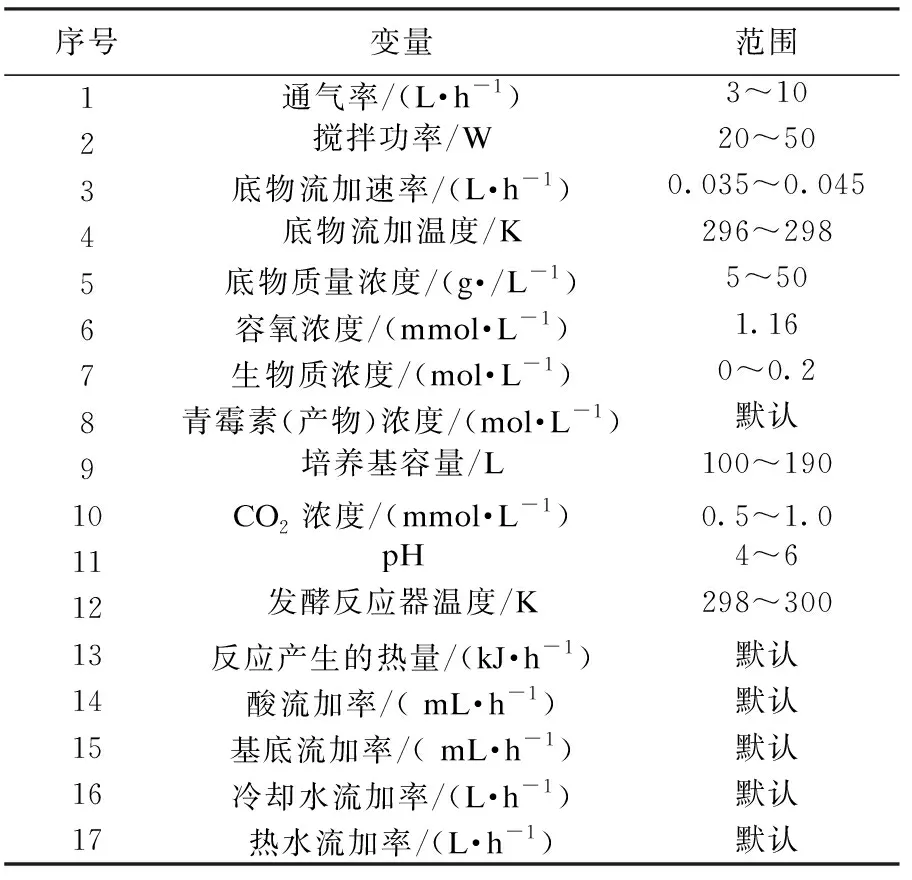
表1 青霉素生产过程的过程变量Table 1 Variables of fed-batch penicillin fermentation process

间歇过程数据通常为三维矩阵，而常见的故障检测方法只能对二维数据进行运算，因此在故障检测前必须对数据进行预处理，即数据展开处理.按时间将各批次的三维数据展开成二维数据，具体展开方式和结果如图1所示.

图1 数据展开方法Fig.1 Data expansion method

图1中i(i=1,2,…,I)表示采样时刻，j(j=1,2,…,J)表示变量.对于任意批次，将数据所有采样时刻的所有变量横向展开即可得到一个1×(400×17)的矩阵，因此所有批次数据全部展开后即可得到一个75×(400×17)的二维矩阵，同理所有故障数据展开后得到的二维矩阵为12×(400×17)维.

为验证方法有效性，本文对于3个工况，发酵200 h时在通风率和搅拌功率上分别加入5 %、10 %的斜坡误差直到结束，每个工况产生4批故障数据，共12个故障批次；从3个工况中分别随机抽取2个批次，共6个批次作为校验批次，加入故障数据，从而得到新的建模数据为69×(400×17)维，新的待检测数据为(12+6)×(400×17)维，即待检测数据共有18个批次，其中前12个批次为故障批次，后6个批次为正常批次.

2.2 基于PCA的故障检测

针对PCA的两个故障检测指标SPE和T2，任意一个指标将批次检测为故障批次则将该批次视为故障批次.图2为采用PCA算法的故障检测结果，由图2可以看出：前12个故障批次全部位于控制限上方，被检测为故障批次；对于校验的6个正常批次，批次13、批次14、批次16、批次17和批次18均误检为故障批次.由此可见，PCA方法存在误报，且误报率很高.

图2 PCA故障检测结果Fig.2 PCA fault detection results

2.3 基于Kmeans-PCA的故障检测

针对传统PCA的故障检测方法误报率过高的不足，提出了一种基于Kmeans-PCA(K-means Principal Component Analysis,Kmeans-PCA)的故障检测方法对PCA算法进行改进.该算法首先采用K-means算法对建模数据进行分类，然后利用PCA算法建模并进行故障检测.K-means聚类结果如图3所示.由图3可知：75个批次的正常数据被分成3类，即这些数据产生于3个不同的批次，这与本文在进行数据采集仿真时的设定一致.本次仿真根据分类结果，分别对不同类别的数据进行检测，每类建模数据为23×(400×17)，待检测为(4+2)×(400×17)，其中前4个批次为故障批次，后2个批次为用于校验的正常批次.图4、图5和图6分别为Kmeans-PCA对3类数据的检测结果.

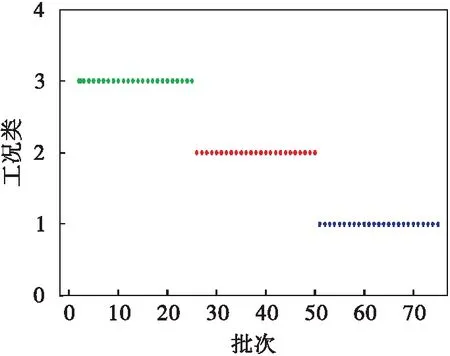
图3 K-means对青霉素数据分成3个工况Fig.3 Penicillin data is divided into three conditions by using K-means

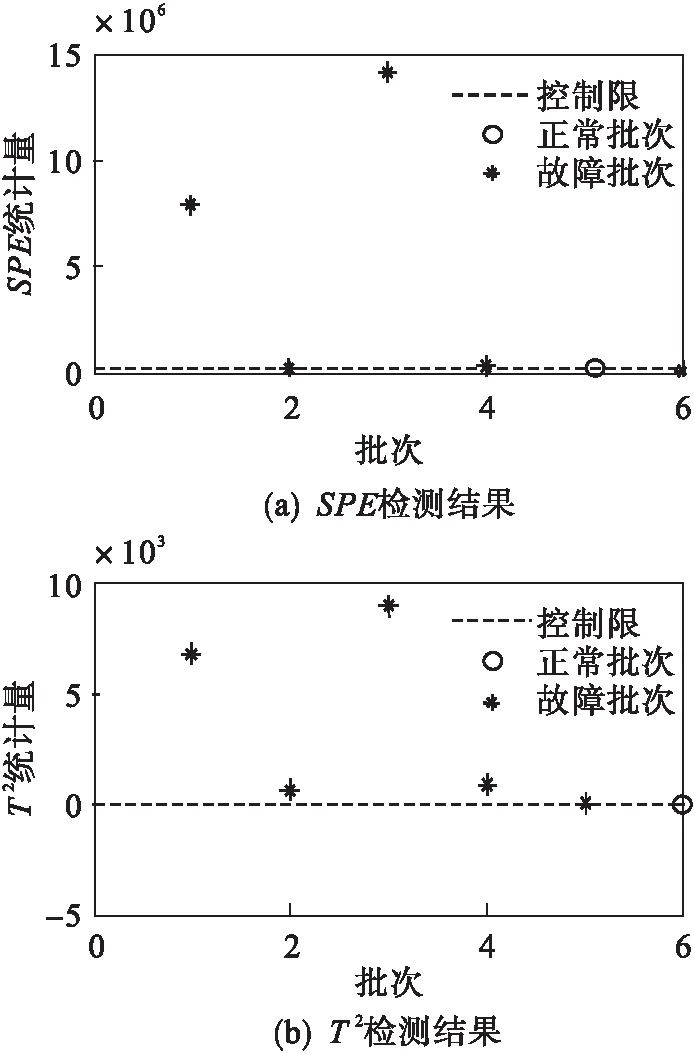
图4 改进的PCA在工况1下的检测结果Fig.4 Improved PCA test results under the first working condition

图5 改进的PCA在工况2下的检测结果Fig.5 Improved PCA test results under the second working condition

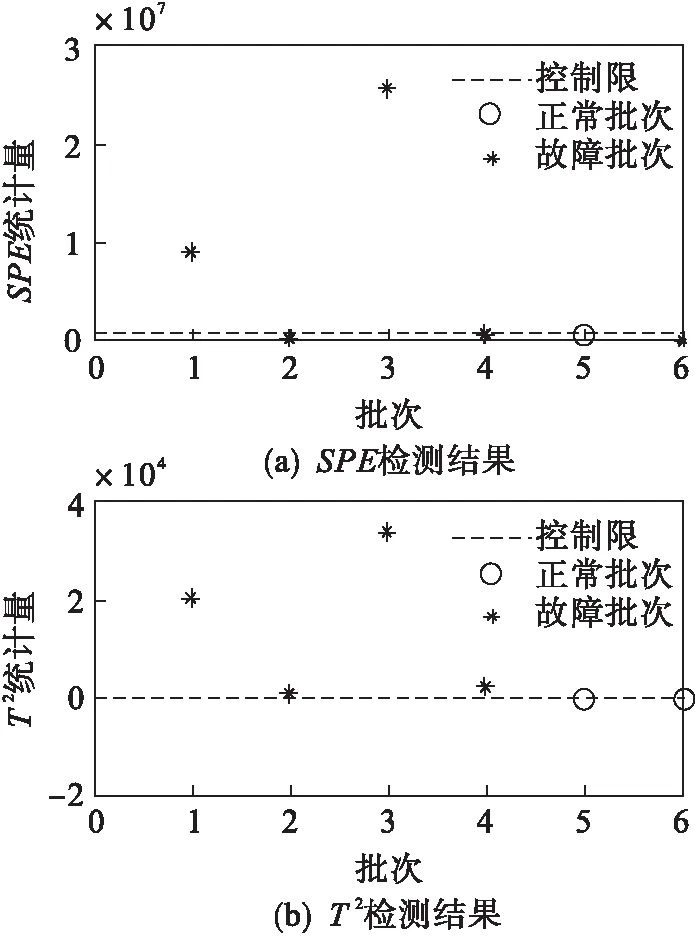
图6 改进的PCA在工况3下的检测结果Fig.6 Improved PCA test results under the third working condition

由图4～图6可知：对于故障批次，不同类别的故障批次均能够被检测；对于检验批次，类别1全部误检为故障批次，类别2和类别3的第6个批次被误检为故障批次.综上所述，Kmeans-PCA方法能根据数据的不同类别分别建模及故障检测，对于故障批次可以有效检测，但对于校验批次，存在误报批次，检测效果并不理想.由于该方法需要对于不同的工况进行分类建模和检测，增加了计算量，导致整体检测时间过长.

2.4 基于K-PCA-KNN的故障检测

针对基于Kmeans-PCA的故障检测方法检测效果不够理想的问题，提出一种基于K-PCA-KNN的故障检测方法.该方法首先利用K-means算法对建模数据进行分类处理，然后采用PCA算法进行数据降维，一定程度上简化计算，最后在主元空间引入k近邻距离统计量进行故障检测.基于K-PCA-KNN的故障检测结果如图7所示，由图7可以看出：故障批次全部被检测为故障批次，检测率达到100 %，校验批次全部被检测为正常批次，误报率为0，由此说明K-PCA-KNN方法能够将故障和正常的批次有效地控制在控制限的上下，具有理想的故障检测效果.

图7 3种工况的K-PCA-KNN检测结果Fig.7 Detection results of three conditions by using K-PCA-KNN

3 结 论

介绍了几种基于数据驱动的复杂工业过程故障诊断中能应用到的算法,如K-means、PCA、KNN等，并采用青霉素发酵过程的数据对这几种方法进行仿真实验.针对青霉素发酵过程具有多阶段的特点，本文提出了一种基于K-PCA-KNN的故障检测方法，该方法使用K-means聚类算法进行分类，然后利用PCA模型提取不同类别的主成分信息，最后在主元空间上建立KNN模型进行故障检测，通过仿真实验验证了该方法的有效性.为后续启动故障诊断机制、准确地诊断事故发生的原因提供良好的故障数据.