Failure treatment strategy and fault-tolerant path planning of a space manipulator with free-swinging joint failure

Gang CHEN,Wen GUO,Qingxuan JIA,Xuan WANG,Yingzhuo FU

School of Automation,Beijing University of Posts and Telecommunications,Beijing 100876,China

KEYWORDS Failure treatment;Fault-tolerant;Free-swinging;Space manipulator;Underactuated

AbstractAiming at a space manipulator with free-swinging joint failure,a failure treatment strategy and fault-tolerant path planning method is proposed in this paper.This method can realize failure treatment of a space manipulator with free-swinging joint failure through determination of the optimal locked joint angle and dynamics model reconfiguration.Fault-tolerant path planning is realized by the establishment of the degraded workspace with integrated kinematics performance(DWWIKP)and an improved A-Star(A*)algorithm.This paper has the following contributions.The determination of the optimal locked joint angle can ensure that the manipulator is able to continue follow-up tasks while maximizing the workspace of the manipulator after locking the fault joint.Underactuated control of a high degree-of-freedom(DOF)manipulator can be effectively solved through dynamics model reconfiguration.The analysis process of the dynamics coupling relationship can be applied to cases where the active joint and the passive joint are parallel or perpendicular to each other.The establishment of the DWWIKP can demonstrate the kinematics performance of the manipulator in both joint space and operation space comprehensively.The improved A*algorithm based on the integrated kinematics performance index(IKPI)can search a fault-tolerant task trajectory that satisfies the requirements of reachability and the overall kinematics performance simultaneously.The method proposed in this paper is verified by a 7-DOF manipulator,and it is available to any DOF manipulator with free-swinging joint failure.

1.Introduction

A higher demand has been proposed for the spatial control capability with the deepening of space exploration1,2.Space manipulators have been widely used in space exploration because of their advantages of large span,flexible operation,and strong load capacity3,4.Space manipulators can be used to replace or assist astronauts to complete complex operation tasks,which can not only reduce the risk of astronauts executing extravehicular activities,but also complete large-scale operation tasks that astronauts cannot complete,such as spacecraft docking,target capture,and large-equipment unit replacement5,6.However,the reliability of space manipulators for long-term orbit service is challenged due to the characteristics of space environment such as ultra-vacuum,high temperature difference,and strong radiation.Furthermore,considering that the joint structure of a manipulator is complex and the components are various,faults of any component can lead to joint failure of the manipulator7.Limited by the hazardous space environment,joint failure usually cannot be repaired at once,and the cost of money and time spent on joint replacement are also extremely high.Therefore,in order to ensure that a spatial operation task can still be completed after joint failure occurs,it is necessary to propose a joint failure treatment method and a fault-tolerant strategy of the space manipulator.

The types of joint failure of space manipulators can be divided into joint locked failure and joint free-swinging failure8.A common treatment method for joint locked failure is to control a degraded manipulator by reconfiguring the model based on the analysis of the kinematics performance of the fault manipulator,and the related research9,10is relatively mature.In this paper,a manipulator failure treatment strategy and a fault-tolerant path planning method for joint freeswinging failure are mainly studied.After joint free-swinging failure occurs,the locked angle of the free-swinging joint needs to be determined first.Then based on the corresponding control strategy,the degraded manipulator with locking the fault joint can be constructed by moving the free-swinging joint to the target angle.Whether the degraded manipulator can complete the given task depends on the kinematics performance,which is affected by the locked angle of the free-swinging joint.Therefore,it is important to determine the optimal locked angle of the free-swinging joint according to the kinematics performance of the manipulator.

To solve this problem,some scholars have carried out relevant research11–14.Tanaka,et al12proposed a comprehensive measurement method of manipulator dexterity based on joint space manipulability ellipsoid,which could reflect the dexterity degradation of a manipulator after joint failure.Bergerman13and Xu14compared the dexterity degradation rates in joint space corresponding to different locked angles of a fault joint,and obtained the optimal joint angle with the least degradation of dexterity.Xu,et al.14evaluated the kinematics performance of a manipulator when the joint was locked at different angles,and obtained a set of joint configurations that met the requirements of kinematics performance including manipulability,condition number,and the minimum singular value.All the above researchers analyzed the kinematics performance in joint space.Although the kinematics performance can be used to determine the optimal locked angle,the kinematics performance in operation space cannot be adequately reflected.Therefore,there are some limitations if only evaluating the kinematics performance in joint space.

Aimed at the influences of joint failure in a workspace,Yang,et al15proposed a collision-free workspace analytical method for planar manipulators based on the extended interior point method,and analyzed the effects of different joint failure angleson thedegradation oftheworkspace.Aydin16investigated the effects of joint failure on the workspace of a manipulator,and used manipulator redundancy to compensate for it.In the above studies,the method for determining the joint locked angle of a manipulator is developed only at the operation-space level.Without considering the influence of the fault joint locked angle on joint space kinematics performance,it may lead to a situation that while the degraded workspace is large,the kinematics performance in joint space is very poor.

Not only the kinematics performance in joint space,but also the scale of the degraded workspace,namely the kinematics performance in operation space,can be affected by the locked angle of the fault joint.However,generally,only one aspect of them is considered in the current research.In order to make the kinematics performances in both joint space and operation space as high as possible,we proposed a method for determining the optimal locked angle of the fault joint while considering the kinematics performance of the manipulator synthetically.

When the optimal locked angle is determined,a manipulator is required to control the fault joint and make it move to the desired angle.According to a manipulator with a freeswinging fault joint,the manipulator becomes an underactuated manipulator due to losing the driving force of the fault joint.The main control methods of underactuated manipulators are sliding mode control17,18,proportion derivative(PD)control19,20,neural network control20,etc.In order to minimize the adjustment time of the underactuated stage,the PD control method with a simple control principle and a short convergence time is chosen in this paper.The current research on PD control mostly aims at low-DOF manipulators;therefore,a high-DOF manipulator can be transformed into a low-DOF manipulator by model reconfiguration.According to studies on manipulator model reconfiguration,Wang,et al.21used the screw theory to realize kinematics modeling for a modular manipulator,which can be applied to fault manipulator model reconfiguration.However,because the screw theory is complex,it is difficult to popularize it in practical applications.Xu,et al.22proposed a kinematic model reconfiguration method for a space station remote manipulator system(SSRMS)-type manipulator with a single joint locked,and obtained the Denavit-Hartenberg(DH)parameters of the reconfigured model.All the studies above are at the kinematics model reconfiguration level,but in order to complete underactuated manipulator motion control with a dynamics coupling relationship between active and passive joints,manipulator dynamics model reconfiguration needs to be carried out.

Therefore,this paper presents a free-swinging joint failure strategy that can optimize the joint-space and operationspace kinematics performances of a degraded manipulator comprehensively.Firstly,the optimal joint locked angle is determined by considering the joint-space and operationspace kinematics performances of the fault manipulator;then through dynamics model reconfiguration,a high-DOF manipulator is equivalent to a low-DOF one with active and passive joints only;finally,PD control is used to adjust the fault joint to the optimal locked angle so as to complete the free-swinging joint failure treatment.

Path planning needs to ensure that a manipulator can continue performing a task after joint failure.Common path planning methods include:A*algorithm23,ant colony algorithm24,genetic algorithm25,particle swarm algorithm26,etc.After a fault joint is locked,some unreachable areas will appear in the normal workspace,which means that the normal workspace is degraded.Therefore,path planning of the manipulator is carried out in the degraded workspace.Thealgorithm is selected as the path planning method as the result of strong autonomy and the ability of avoiding the unreachable areas effectively.Considering that the kinematics performance of the manipulator decreases after the joint failure,it is necessary to optimize the kinematics performance of the manipulator in path planning.Roberts27introduced a degraded manipulability optimization term in the process of planning to make a manipulator highly operable.Zhao,et al28designed a faulttolerant path planning algorithm which regarded centrality as the kinematics performance index to realize the optimization of the manipulator trajectory.Ralph and Pai29used the minimum constraint criterion to propose a path planning method for manipulator self-repair after joint failure,so that a space manipulator can maintain a high kinematics performance under the constraint of motion.The fault-tolerant path planning methods in the above studies are generally aimed at a single performance index,so it may lead to a low comprehensive performance of the planned path.In this paper,the problem which arises from a single kinematics performance index is solved by introducing an optimization term with multiple kinematics performance indices into the cost function of the A*algorithm.

In summary,aiming at a space manipulator with a freeswinging fault joint,a failure treatment strategy and a faulttolerant path planning method are proposed in this paper,where failure treatment consists of two parts:optimal locked angle and joint adjustment.The main contributions of this paper include the following.Firstly,a method for solving the optimal locked joint angle considering the kinematics performances of both joint space and operation space is proposed,which guarantees an optimal kinematics performance of the degraded manipulator.Secondly,a method combining dynamics model reconfiguration with underactuated motion control is proposed to solve the problem of free-swinging joint adjustment,and it can realize motion control and locking of the freeswinging joint;therefore,it is free from the limitation of the DOFs of the manipulator.Finally,the DWWIKP is established based on an IKPI,and by introducing the IKPI to the cost function of the improvedalgorithm,fault-tolerant path planning of the space manipulator is realized.The trajectory searched by this method can satisfy the requirements of reachability and comprehensive kinematics performance.The method presented in this paper is universal and suitable for any joint at any angle of a manipulator with any degree of freedom.

Fig.1Initial configuration of an SSRMS-type manipulator.

The rest of this paper is organized as follows:the second chapter carries out research on a method for solving the optimal locked angle of a fault joint;the third chapter finishes motion control;the fourth chapter carries out research on fault-tolerant manipulator path planning;the fifth chapter carries on simulation to verify theoretical research results;the sixth chapter summarizes the full text.

2.Determination of optimal locked angle of a fault joint for a space manipulator

When free-swinging failure occurs in a joint,because of its loss of driving force,if not given restrained control,it is likely to cause the manipulator collide with obstacles outside or the manipulator itself,affecting the completion of the follow-up task of the manipulator,so the free-swinging fault joint must be locked in a fixed angle.According to the literature12–16,we can see that the locked angle of a joint has a great influence on the kinematics performances of a manipulator in both joint space and operation space.Since the current research mainly focuses on the kinematics performance in just one of them,in order to give full play to the kinematics performance of a joint-failure manipulator,the kinematics performances of the manipulator in the joint space and the operation space are both taken into consideration in this paper,and a method of determining the optimal locked angle of the joint is studied.

2.1.Establishment of kinematic model

In this paper,a 7-DOF SSRMS-type manipulator is taken as the study object,as shown in Fig.1,and it contains three shoulder joints,an elbow joint,and three wrist joints.The kinematic model is established by the DH parameter method,in which coordinate O0x0y0z0represents the basic coordinate system R0,and Oixiyizi(i=1,2,...,7)represent the ith link coordinate system Ri.

2.2.Determination of optimal locked angle of a fault joint

Kinematicsperformanceindicesin jointspaceofthe manipulator include:manipulability,condition number,the minimum singular value,task continuity,etc.Since manipulability,condition number,and the minimum singular value can comprehensively characterizethekinematicsperformance in joint space,these three kinematics performance indices in joint space are selected as the basis for determining the optimal locked angle of the manipulator,and their meanings14are shown in Table 1,where subscript ‘f’means‘failure’.

In this paper,the configurations set is firstly obtained;then the optimal set is determined by analyzing the degraded manipulability,the condition number,and the minimum singular value of the configurations set in joint space.Furthermore,the optimal joint locked angle of the manipulator is determined by further analyzing the reachable workspace of the optimal set,and a specific example of the optimal locked angle of the manipulator is given as follows.

Table 1Meanings of performance indices.

(1)Determination of configurations set

In the actual operation of the manipulator,considering the continuity of a task,it is necessary to ensure that the end position and attitude of the manipulator are consistent before and after the failure joint is locked.The determination of the optimal locked angle of the fault joint needs to be carried out under the same end position and attitude.For a 7-DOF manipulator,when a joint is locked,it is degraded into a 6-DOF manipulator,and theoretically speaking,up to eight configurations corresponding to the given end position and attitude can be obtained.Therefore,when the fault joint traverses its motion range at a certain step size,the configurations set A under the current position and attitude is obtained.

(2)Determination of optimal configuration set

Through the singular-value decomposition of the Jacobian matrix corresponding to different joint configurations in the configuration set A,the degraded manipulability,the degraded condition number,and the degraded minimum singular value corresponding to each joint configuration can be calculated.Setting the threshold of each kinematics performance index respectively,the optimal configuration set B that meets the requirement of joint space kinematics performance can be obtained,and the fault joint angles contained in the optimal configuration set B constitute of the optimal fault joint locked angle set C.

(3)Solution of optimal fault joint locked angle of fault joint

After the joint failure occurs,the reachable workspace of the manipulator is degraded,and the joint locked angle affects the degraded degree of the manipulator workspace.By analyzing the degraded workspace corresponding to set C,the angle corresponding to the maximum degraded workspace is selected as the optimal angle of the fault joint.

For the sake of clarity,taking the 7-DOF manipulator shown in Fig.1 as an example,the optimal locked angle of the fault joint is solved as follows.

Step 1 When free-swinging failure occurs in any joint among the 1st,2nd,6th,and 7th joints,since the 3rd,4th,and 5th joints belong to healthy joints and the three axes are parallel,the optimal locked angle of the fault joint can be solved directly by an analytical method25,to Step 2;when joint failure occurs to any joint among the 3rd,4th,and 5th joints,since there is no parallel or intersection of the three adjacent joint axes,it is necessary to use analytical and iterative methods22,to Step 3.

Step 2 Taking the failure of the 1st joint as an example,the range of motion is traversed at a given angle step size,and the kinematic equation is established according to the known end position and attitude as

Moving the known items in Eq.(1)to the left of the equal sign gets

According to Eq.(2),12 analytical equations can be obtained,and the analytical expression of the unknown joint angle can be obtained.There will be 8 sets of solutions at most.After traversing the fault joints,the configuration set A under a certain position and attitude of the end-effector of the manipulator can be established,to Step 4.

Step 3 The manipulator is modified by setting the offset of the link to zero to construct a spherical joint where the three axes intersect at one point.The inverse kinematics solution of the modified manipulator can be obtained by the analytical method in Step 2;the deviation caused by zeroing of the offset is eliminated by the iterative method to obtain the inverse kinematics solution of the actual manipulator.After traversing the fault joints,the configurations set A can be established under a certain position and attitude of the end-effector of the manipulator,to Step 4.

Step 4 Calculate the degraded Jacobian matrix Jf(Jf2 R6?7,where subscriptmeans ‘failure’)corresponding to each joint configuration in the configuration set A as follows:

where k is the fault joint label.Eq.(3)is subjected to singularvalue decomposition as

where U represents a 6?6 orthogonal matrix,is a 6?7 diagonal matrix with a diagonal of non-negative real number,V denotes aorthogonal matrix,andhas the following form:

where the diagonal terms r1,r2,...,r6are the singular values of the degraded Jacobian matrix Jf,and r1?r2?...?r6,in which r6represents the minimum singular value.

Step 5 According to Eq.(6),the degraded manipulability,the degraded condition number,and the degraded minimum singular value corresponding to each configuration in the confi guration set A are calculated respectively as follows:

It can be seen from Table 1 that the greater the value of xf,the better the dexterity of the manipulator,and when xf=0,the space manipulator is currently in a singular configuration,so the smaller the value of cf,the closer the manipulator’s ability to move in all directions,and the greater the value of sf,the higher the motion ability of the manipulator in the worst direction.

Step 6 Setting the thresholds for the degraded manipulability,the degraded condition number,and the degraded minimum singular value as j,k,and v,respectively,according to the principle of satisfying xf>j,cf>k,and sf>v,the optimal set B which satisfies xf>j,cf>k,and sf>v can be selected from the configuration set A,and the fault joint angle corresponding to each of the joint configurations in the optimal set B constitutes an optimal fault joint locked angle set C.

Step 7 Aiming at the locked angle fiin the optimal fault joint locked angle set C,according to the forward kinematics equation,the Monte Carlo method30is used to traverse the joint rotation angleand the degraded workspace Wf(subscript ‘f’means ‘failure’)can be obtained as

Step 8 The degraded workspace is enclosed in a rectangular with length a,width b,and height c.The degraded workspace is rasterized,and the grid side length is Dl=min(a,b,c)?q,where q is the grid scale value.In this case,V can be rasterized into a set of grids with a length of Dl,and the total number of grids is,where V represents the volume of the rectangular,andis the rounding-up operation,which can make the grid number as an integer.Since the scatters in the degraded workspace of the manipulator are irregularly distributed,the volume of the workspace cannot be accurately calculated,but one grid is a small cube with a certain volume;therefore,the number of grids with scattered points can be multiplied by the grid volume to approximate the volume of the degraded workspace.

Step 9 The total number P of grids containing scatter points in the degraded workspace Wfis calculated.By comparing the total number of grids included in the degraded workspace,it is able to compare the volumes of different degraded workspaces,and select the angle ficorresponding to the largest degraded workspace as the target locked angle.The joint configuration corresponding to fiis the desired configuration of the manipulator when the fault joint is locked.

According to the method above,it is able to determine the optimal locked angle of the fault joint of the manipulator,which can maximize the degraded workspace after the fault joint is locked under the premise of ensuring the kinematics performance in joint space of the manipulator.

3.Configuration adjustment strategy of a fault manipulator based on underactuated control

The angle needs to be adjusted in order to lock the fault joint at the optimal angle.Considering the free-swinging failure of the joint,the joint is in an underactuated state,and the manipulator is degraded into an underactuated manipulator,which needs to be controlled by an underactuated control method.According to the literature17–20,the current research on underactuated control is mainly for a low-DOF plane manipulator,and the method is generally applicable to a case where the active joint axis and the passive joint axis are parallel to each other.However,for a high-DOF space manipulator,especially the case where the active joint axis and the passive joint axis are perpendicular to each other is lack of research.In order to realize its underactuated control,we present a method of fault joint adjustment of a high-DOF underactuated manipulator based on the dynamics coupling relationship.The method is based on reconfiguration of the dynamics model of the high-DOF manipulator,which applies an underactuated control method on the manipulator using the dynamics coupling relationship between the joints to adjust the fault joint to the optimal locked angle.This method can solve the problem of angle adjustment when free-swinging-type failure occurs in any joint of the high-DOF manipulator,and it can be applied to the case where the active joint and the passive joint are parallel or perpendicular to each other.

3.1.Reconfiguration of dynamics model of manipulator

In underactuated control of the manipulator,the passive joint is usually actuated by the active joint based on the dynamics coupling relationship.Compared with the low-DOF manipulator,the dynamics coupling relationship between the joints of the high-DOF manipulator is more complicated.In order to simplify the analytical process of the dynamics coupling relationship,on the basis of establishing the conventional dynamics model of the manipulator,a general high-DOF manipulator model reconfiguration method is proposed.It can be applied to failure treatment of arbitrary fault joints of the manipulator to simplify the dynamics coupling relationship between the active joint and the passive joint,and to facilitate the follow-up underactuated control of the manipulator.

3.1.1.Dynamics modeling of manipulator

For the normal 7-DOF manipulator,establish the following simplified model as shown in Fig.2(a).In the figure,Rkdenotes the coordinate system of link Lk,Jkdenotes the joint betweenand Lk,lkdenotes the vector connecting joints Jkto Jk+1,rkdenotes the vector of the centroid of link Lkwith respect to the coordinate system,rk,irepresents the vector of the centroid of link Liin the coordinate system,and mkrepresents the mass of link Lk.

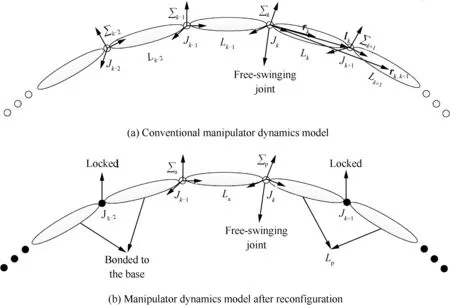
Fig.2Numbering of the manipulator dynamics model before and after reconfiguration.

3.1.2.Reconfiguration of dynamics model of manipulator

In the case of underactuated control for the manipulator,two treatment schemes can be implemented:one scheme is taking the front healthy joint adjacent to the passive joint(fault joint)as the active joint to actuate the passive joint,and the other scheme is taking the next healthy joint adjacent to the passive joint as the active joint to actuate the passive joint.According to an analysis of the dynamics coupling characteristics of an underactuated manipulator31,it can be seen that for a 2-DOF manipulator,when the 1st joint is in the active state,the acceleration coupling and the torque coupling between the active joint and the passive joint are more obvious than those of the 2nd joint in the active state.Therefore,the front joint is selected as the active joint to actuate the passive joint to obtain greater acceleration and driving force in this paper,but when the 1st joint fails,because there is no front joint,then the 2nd joint is selected as the active joint.Without loss of generality,the dynamics model reconfigurations and the dynamics coupling relationship analysis methods of the front joint and the next joint in underactuated control of the fault joint are similar;therefore,this paper only describes the front joint as the active joint.

In order to simplify the analysis process of the dynamics coupling between the active joint and the passive joint,and to avoid the control process being affected by other joints except for the active joint and the passive joint,it is necessary to temporarily lock the rest of the joints.At this point,the joints between the ground and the active joint are fixed to the ground to form a base,and the joints between the passive joint and the end-effector are fixed as a link at the end of the passive joint,so the manipulator can be equivalent to a 2-DOF manipulator.

He came to a wide heath,4 on which nothing was to be seen but a circle of trees;5 under these he sat sorrowfully down, and began to think over his fate

For an n-DOF manipulator,when joint Jkfails,joints J1,are locked at the current angles...,.As shown in Fig.2(b),links L1,L2,...,Lk?2are fixed to the base,link Lk?1is an active link La(subscript ‘a’means ‘active’),and links Lk+1,Lk+2,...,Ln,and Lkare fixed as a passive link Lp(subscript‘p’means‘passive’).Re-establish the coordinate system Raof La(coincident with the original coordinate system)and the coordinate systemof Lp(coincident with the original coordinate system).At this time,the manipulator is transformed into a 2-DOF manipulator consisting of active joint Jk?1and passive joint Jkonly.In order to obtain the dynamics parameters of the passive link Lp,the following solution is required:

According to Eq.(8),the vector rp,iof the mass center of link Li(i=k+1,k+2,...,n)involved in link Lprelative to the coordinate system Rpis

Through the above method,it is able to complete the dynamics model reconfiguration after the free-swinging joint failure of the manipulator.The 7-DOF manipulator is equivalent to the 2-DOF manipulator only containing the active joint and the passive joint,and its reconfigured parameters are the active link La,the passive link Lp,the coordinate systems Raandand the vector rp,iof the mass center of link Li(i=k+1,k+2,...,n)involved in link Lprelative to the coordinate systemto support the follow-up underactuated motion control.

3.2.Configuration adjustment of underactuated manipulator based on dynamics coupling relationship

In order to adjust the fault joint to the optimal locked angle,underactuated control of the fault manipulator is required.In this paper,the adjustment strategy of the underactuated manipulator contains two stages:passive joint adjustment and healthy joints adjustment.Specifically,lock the rest joints except for the active joint and the passive joint firstly;based on the dynamics coupling relationship between the active and passive joints,actuate the active joint to make the passive joint move to the desired position;lock the passive joint.Then unlock the healthy joints,move them to the desired position,and complete the underactuated adjustment of the manipulator.

3.2.1.Strategy of passive joint adjustment

3.2.1.1.Analysis of dynamics coupling relationship.At present,for the adjustment of passive joints,a large number of studies have focused on the case that the active joint axis is parallel to that of the passive one,but due to the complexity of the configuration of high-DOF manipulators,the case that the active joint axis and the passive joint axis are parallel to each other and the case that they are perpendicular to each other both exist,making the coupling relationship between the active and passive joints more complex.Therefore,aiming at the two cases respectively,the Lagrangian method is used to solve the dynamics equation of the manipulator,and the dynamics coupling relationship between the active and passive joints is obtained in this paper.Based on this idea,the dynamics coupling relationship of other position relations between the active joint axis and the passive joint axis can also be solved.

Case 1:the active joint axis is perpendicular to the passive joint axis

The kinetic energies of links Laand Lpare

According to Eq.(10),the total kinetic energy of the system is

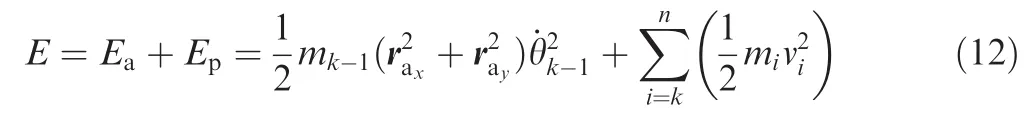
Since the gravitational potential energy G in the space environment is zero,the Lagrangian equation is

According to Eq.(13),the torques saand sp(subscripts ‘a’and ‘p’represent ‘active’and ‘passive’,respectively)of the active and passive joints are

During the process of underactuated joint adjustment,the torque that the passive joint can actively provide is zero.Considering the friction in the joint,the friction torque sf(subscript ‘f’represents ‘friction’)is relative to the angular velocity of the passive joint by using the viscous friction model as

where l represents a viscous friction factor.

The actuating torque of the passive joint in Eq.(14)can be transformed into

Substituting Eq.(17)into Eq.(16),the dynamics coupling relationship between the active and passive joints can be obtained as follows:

Case2:the active joint axis is parallel to the passive joint axis

The kinetic energies of links Laand Lpare

Among them,the linear velocity viof the centroid of each link Liinvolved in link Lprelative to the coordinate systemis

Follow-up steps equate to Eqs.(12)–(18),so the dynamics coupling relationship between the active and passive joints can be obtained as follows:

3.2.1.2.Passive joint angle adjustment based on PD control.In this paper,the PD control method is used to control the active joint and adjust the passive joint to the desired angle by the dynamics coupling relationship between the active joint and the passive joint described in Eqs.(18)and Eq.(21).The PD control law for the active joint is

where subscripts‘p’and ‘d’represent‘proportion’and ‘derivative’,respectively,xnand n represent the undamped natural frequency and damping ratio of the system,respectively,and the value ofaffects the effect of position control,i.e.,>1,over damping;=1,critical damping;0<<1,underdamping.

Adjusting the active joint angle according to Eq.(22),the passive joint can reach the desired position,and a global stability control in joint space can be realized.

Through the study above,we can use the dynamics model reconfiguration method to equalize a high-DOF manipulator to a 2-DOF one which only includes the active joint and the passive joint.By analyzing the dynamics coupling relationship between the active joint and the passive joint and combining with the PD control method,the passive joint can be adjusted to the desired angle.This method is applicable to cases where the active joint and the passive joint are parallel or perpendicular to each other.

3.2.2.Strategy of active joint adjustment

After adjusting the passive joint,to adjust the rest of the joints to the desired configuration,we lock the failed joint and unlock the rest healthy joints.At this time,the manipulator is transformed into an(n?1)-DOF manipulator,and links Lk?1and Lkadjacent to joint Jkcan be fixed as a new link by the method described in Eqs.(8)and Eq.(9).Then we calculate the dynamics parameters of the new connecting link.

The known dynamics model of the manipulator is

According to the dynamics model of the manipulator,the healthy joints can be moved according to the desired position by PD control,and a global stability control in joint space can be realized.

4.Fault-tolerant path planning for the manipulator by an improvedalgorithm

In order to complete spatial tasks after single-joint locked failure,it is necessary for the manipulator to search a reachable trajectory connecting the initial point and the desired point in the degraded workspace.Namely,we carry out a research about fault-tolerant path planning for the manipulator.It can be known that some cavities(unreachable regions)may appear in the degraded workspace,and the manipulator needs to avoid them during its movement.Considering that thealgorithm has the capability to avoid cavities,a fault-tolerant path is searched by thealgorithm in this chapter.The trajectory searched by thealgorithm in the degraded workspace meets the requirements of reachability,but when moving along the trajectory,there may occur the problem that the kinematics performance in joint space is too poor to accomplish tasks successfully.Based on establishing the DWWIKP,a fault-tolerant path planning method is proposed by an improvedalgorithm in this paper,which guaranteesthatthesearched trajectory meetsthetask requirements of reachability and kinematics performance.Specifically,the IKPI in joint space is constructed firstly,and based on the generation of the degraded workspace,the DWWIKP of the manipulator is established by the IKPI.The IKPI item is integrated to the evaluation function to improve thealgorithm,and then fault-tolerant path planning is completed by the improvedalgorithm in the DWWIKP.

4.1.Establishing the DWWIKP of manipulator

In order to search a trajectory that meets the task requirements of reachability and kinematics performance after single-joint locked failure,it is important to establish a workspace that can characterize the reachability and kinematics performance of the degraded manipulator.The reachability can be characterized by the degraded workspace,and for reflecting the kinematics performance,it is necessary to evaluate the IKPI of the manipulator when its end-effector reaches each point in the degraded workspace.In this paper,the IKPI is constructed by integrating different kinematics performance indices in joint space,and the DWWIKP that can characterize the reachability and kinematics performance simultaneously is established.

4.1.1.Constructing IKPI

For characterizing the IKPI of the manipulator in joint space when the end-effector is located at each point in the degraded workspace,theIKPIisconstructed byintegrating the degraded manipulability xf,the degraded condition number cf,and the degraded minimum singular value sf.

The degraded manipulability,the degraded condition number,and the degraded minimum singular value of the manipulator can be computed by Eq.(6).Due to the different ranges of values of these indices,a normalized process is necessary for them.Assuming that[i,j]is the range of the kinematics performance index x,then we can gain the normalized process as

where normal(?) represents the normalized process for x.

Because the higher xf,sfand the lower cf,the higher kinematics performance,the IKPI of the manipulator could be written as

A higher u means a better IKPI of the manipulator.

4.1.2.Establishing the DWWIKP by IKPI

The establishment of the DWWIKP is based on the degraded workspace of the manipulator in this paper.The kinematics performances for different configurations,which correspond to the cases that the end-effector of the manipulator is located at different points,can be evaluated by the IKPI.Furthermore,the evaluations of the reachability and kinematics performance of the trajectory can be completed by combining the IKPI value with the points included in the degraded workspace.The establishment of the DWWIKP is the foundation for follow-up fault-tolerant path planning with the improvedalgorithm.

The degraded workspace Wfof the manipulator can be generated by combining Eq.(7)with the Monte Carlo method.The arbitrary scatter pj=(xi,yi,zi)in Wfoften reflects multiple sets of joint angles,to which the IKPI values of the manipulator corresponding can be computed by Eq.(26).For security,we regard the minimum IKPI value ujamong them as the one of the manipulator when its end-effector reaches at scatter pj.Supposing that=(xi,yi,zi,uj),when joint failure occurs,the DWWIKPof the n-DOF manipulator can be shown as

Based on Eq.(27),the procedure for the establishment of the DWWIKP can be shown as follows.

Step 1 Consider the case of single-joint failure,confirm the fault joint and the optimized locked angle,and establish the degraded workspace Wfby the Monte Carlo method.

Step 2 Solve the IKPI value ujof the manipulator when the end-effector is located at scatter pjin the degraded workspace by the constructed IKPI.

Step 3 Build the mapping form ujto pj,and complete the establishment of the DWWIKPof the manipulator.

Step 4 Figure the color graph forto show the established DWWIKP intuitively.

The established DWWIKP,which can characterize the reachability and IKPI of the manipulator simultaneously,is a comprehensive characterization method for the kinematics performances in operation space and joint space.A trajectory that meets the requirements of the reachability and IKPI can be searched in the established DWWIKP.

4.2.Fault-tolerant path planning via improvedalgorithm

In order to search a trajectory that meets the requirements of the reachability and IK PI simultaneously in the DWWIKP,

4.2.1.DWWIKP rasterizing

For searching a fault-tolerant path via the improvedalgorithm,it is foundational to rasterize the established DWWIKP.Based on Step 8 of the solution process for the optimal locked angle of the fault joint in Section 2.2,the DWWIKP is rasterized into Nc(subscript‘c’means ‘cube’)small cubes whose side length is equal to the searching step Dl.Dl can be determined due to the method in Step 8 of Section 2.2 and the constraint in Eq.(29).For security,the minimum value of the IKPI corresponding to all scatters contained in a certain grid is identifi ed as the IKPI value of the current grid,which is shown as

In addition,to prevent the appearance of vacancy in a theoretically reachable area caused by insufficiency of random space scatters,the ratio of the total number of random scatters to that of small cubes is required to be higher than a specific value e,i.e.,

4.2.2.Trajectory searching via improvedalgorithm We search a trajectory that meets the requirem ents of the

r

eachability and IKPI simultaneously by thealgorithm in the rasterized DWWIKP.The traditionalalgorithm is a heuristic searching method.Based on its evaluation function shown as Eq.(30),the moving cost corresponding to all space points can be characterized to search a trajectory meeting the requirement of reachability as follows:

In the evaluation function,g(e)denotes the cost from the initial grid to the current grid e,while h(e)denotes the cost from the current grid e to the target.The sum of them is the total cost value of the current grid.When searching a task trajectory,the grid with the lowest f(e)is selected as the next intermediate grid all the time.

In order to obtain a trajectory satisfying the requirement of the IKPI,the evaluation function of thealgorithm is improved by taking the IKPI values of grids into account.The improved evaluation function is shown as

where u(e),denoting the cost for the IKPI of grids,is in inverse proportion to Ue,which can be written as u(e)=r/Ue.r,which reflects the IKPI influence degree to f(e),denotes the cost coefficient for the IKPI.Grids with a higher IKPI value would be selected when searching a trajectory by increasing the value of r,which means that the IKPI of the searched trajectory is improved,while decreasing r leads to a bad IKPI of the searched trajectory.As a result,it is confirmed according to real task requirements.

When there is a minimum limit for the IKPI to complete follow-up fault-tolerant tasks,assuming that the value is Umin,if Ue

4.2.3.Optimizing trajectory

The original searched trajectory may contain too many intermediate points because of the characteristic of the A*algorithm.In this way,the manipulator needs to stop and start when moving through the intermediate points,which leads to severe component abrasion and resource consumption.Therefore,in order to avoid frequent starts and stops of the manipulator,it is necessary to decrease the number of intermediate points with the searched trajectory,which makes it possible to optimize the original searched trajectory.

Point collection Oais assumed to store the intermediate points of the original trajectory searched by the traditional

Step 2 If Ueof grids which are passed by pathis greater than the minimum IKPI which is determined by task requirements,turn to Step 3;otherwise,turn to Step 4.

Step4Remove intermediate pointsFinish the optimization of set Oa,and express it aswhereandRegard set Oa0as set Oa.Regard pointin set Oa0as the start pointin set Oa,and turn to Step 5.

Step 5 If k

A task trajectory connecting a few intermediate points is obtained by the optimization method above,which completes the optimization for the original searched trajectory.

According to the research above,by rasterizing the established DWWIKP and evolving the traditionalalgorithm through integrating the IKPI item into the evaluation function,the search of a trajectory meeting the requirements of the reachability and IKPI is completed.The optimization for the searched trajectory is achieved by reducing the number of intermediate points,which improves the quality and efficiency of fault-tolerant path planning for the manipulator.

5.Simulation

In this paper,the 7-DOF manipulator,shown in Fig.1,is regarded as the research object for simulation.Its DH and dynamicsparametersareshown in Tables2and3,respectively.

Being directed at a specific task,assuming that the initial manipulator configuration isthe initial position and attitude of the end-effector areand the desired position isJ2is the fault joint.

Table 2DH parameters of SSRMS-type manipulator.

Table 3Dynamics parameters of SSRMS-type manipulator.

Fig.3Different volumes of degraded workspaces reflecting different locked angles.

5.1.Analyzing optimal locked angle for fault joint

Traversing the angle of J2by 1?in the range of[?180?,180?],2384 sets of configurations,which come from configuration set A,are obtained by solving the inverse kinematics for the start position and attitude of the end-effector.Computing the degraded manipulability,the degraded condition number and the degraded minimum singular of the manipulator for different configurations in set A,as well as 119 sets of configurations,which constitute of set B,are selected by assuming that the corresponding thresholds are j=100,k=9,and v=0.85.The obtained set B reflects 79 locked angles for the fault joint,which form set C.

The degraded workspaces of the manipulator,whose fault joint is locked at different angles in set C,are formed by 50000 scatters generated by the Monte Carlo method through traversing 50000 sets of joint angles.The reflection from the locked angles to the volumes of the degraded workspaces,shown in Fig.3,is obtained by rasterizing the workspaces.Fig.3 shows that the biggest volume of the degraded workspace can be obtained when the fault joint is locked at 92?.The corresponding configuration is[114.46?,92?,46.85?,105.59?,?75.09?,?77.02?,?160.61?].The selected locked angle of the fault joint is the result obtained by synthetically considering the kinematics performances in joint space and the workspace.

5.2.Adjusting manipulator configuration via underactuated control

5.2.1.Adjusting passive joint

When free-swinging failure occurs in J2,its angle is going to be adjusted by regarding the front joint J1as the active joint.Based on Fig.1,the axes of the active joint J1and the passive joint J2are perpendicular to each other.Therefore,the dynamics coupling relation between J1and J2is shown as Eq.(18).

Locking J3-J7and reconfiguring the dynamics model of the manipulator,L1=Lais the active link,and links L2-L7are locked together as the passive linkLp.Theposition vectors of the centroid relative to the coordinate Rpfor each link Liinvolved in Lpare shown asm,m,m,rp6

Fig.4Changing curves for joint angles to adjust angle of passive joint.

Fig.5Changing curves for angles of joints J1,J3?J7.

Fig.6Degraded workspace of 7-DOF manipulator with locked J2.

Based on the dynamics coupling relation and PD control,the changing curves of the angles of the active and passive joints are shown in Fig.4.From Fig.4,we can know that in 8 s,the active joint stops moving with its angle staying at 19.94?,and because of the inertia,the passive joint cannot stop moving until the time is 35 s,which makes the angle of J2arrive at the desired locked angle of 92?.

5.2.2.Adjusting active joint

Lock the fault joint when it is adjusted to the desired locked angle,unlock joints J3-J7,and then regard links L1and L2as a new link bound together.

Knowing that the initial angles of joints J1,J3?J7areand the desired joint anglesarethe changing curves for the angles of joints J1,are shown in Fig.5.

Fig.7Kinematics parameters of 7-DOF manipulator with locked J2.

5.3.Analyzing degraded workspace of manipulator

The degraded workspace of the 7-DOF manipulator is analyzed by the Monte Carlo method with the fault joint J2locked at 92?.Setting the motion ranges of normal joints to[?180?,180?],the workspace and its exterior envelope of the normal manipulator is shown in Fig.6 via traversing 200,000 sets of joint angles(coordinate OXYZ in Fig.6 is the basic coordinate O0x0y0z0).Meanwhile,it is known that there is an unreachable area in the workspace through analyzing its sectional view as shown in Fig.7.

The results,shown in Fig.7,are the analysis of the kinematics performances corresponding to a single index and the IKPI with the end-effector located at the scatters in the degraded workspace.From Fig.7,based on a single index to analyze the kinematics performance,the scatters with better kinematics performance are distributed in different regions.However,based on the IKPI,the scatters are distributed at the intersection crossed by the above obtained different regions.Then the DWWIKP,which can simultaneously characterize the reachability and IKPI of the manipulator,is established based on the degraded workspace and IKPI.

Fig.8Searched linear trajectory in degraded workspace.

5.4.Fault-tolerant path planning for fault manipulator

The 7-DOF manipulator is degraded to a 6-DOF one with joint J2locked at,and its degraded workspace is covered by a large cuboid,whose length,width,and height are 22,22,and 21 m,respectively.Setting the side length of the grids as Dl=0.5 m,we can rasterize the degraded workspace as shown in Fig.6.

Knowing that the position of the start point ism,and the position of the desired point is[4.50,2.40,0.30]m,the linear trajectory,shown in Fig.8,is searched in the degraded workspace with joint J2locked.Evidently,there is an unreachable section in the searched trajectory,so it is necessary to plan a fault-tolerant path by using the A*algorithm.

Assuming that the cost coefficient of the IKPI is r=5,and the lowest IKPI is Umin=1.2,then the trajectory shown in Fig.9(a)is searched by the improved A*algorithm.Fig.10(a)characterizes the IKPI values of grids including intermediate points of the searched trajectory,and the values lie in the range of 1.3–2.3.It is shown that the grids corresponding to higher IKPI values are selected preferentially.The optimized trajectory shown in Fig.9(b)is obtained by reducing the number of intermediate points,and the IKPI corresponding to its intermediate points is shown in Fig.10(b).The number is degraded evidently by comparing the numbers of intermediate points involved between the original and optimized trajectories.Meanwhile,the IKPI of the optimized one meets the task requirements by analyzing Fig.10(b).

For comparison,the trajectory shown in Fig.9(c)is searched by the traditional A*algorithm,whose evaluation function doesn’t contain the improved term.The IKPI values corresponding to the intermediate points of the trajectory are shown in Fig.10(c).Because of the situation that some IKPI values corresponding to the intermediate points are less than Umin,the trajectory searched by the traditional A*algorithm cannot meet the task requirements.

According to the simulation results,the optimal locked configuration selected in this paper can guarantee the kinematics performances in joint space and the workspace simultaneously.Based on the dynamicscoupling relation,the adjustment for configuration of the fault manipulator is achieved by underactuated control with the arbitrary joint being free-swinging.Meanwhile,the kinematics performances in joint space and the workspace can be characterized by the established DWWIKP.Thetrajectorysearched bythe improved A*algorithm can not only guarantee the reachability,but also meet the requirement of the IKPI of the manipulator.

Fig.9Trajectories searched by A*algorithm.

Fig.10IKPI values corresponding to points of trajectories.

6.Conclusions

The failure treatment strategy and fault-tolerant path planning for a manipulator with free-swinging joint failure are studied in this paper.Firstly,the optimal locked angle of the fault joint is solved based on a comprehensive analysis of kinematics performance indices and the degraded workspace;secondly,the high-DOF manipulator is equivalent to a low-DOF one to realize dynamics model reconfiguration,and based on the underactuated control strategy,the fault joint is locked in the optimal locked angle;then,through the normalization of the joint space kinematics performance index and combiningfinally,the traditionalalgorithm is improved by adding the IKPI to its cost function,and searching of a task trajectory based on the improvedalgorithm is realized.

The main contributions of this paper are as follows.The optimal locked joint angle proposed in this paper ensures that the manipulator is still able to complete follow-up tasks while maximizing the workspace of the manipulator after locking the fault joint.Through dynamics model reconfiguration,the underactuated control strategy is realized,and the control of the high-DOF manipulator can be effectively solved.The establishment of the DWWIKP can demonstrate the kinematics performance of the manipulator in both joint space and operation*space comprehensively.Com*pared with the traditional Aalgorithm,the improved Aalgorithm based on the IKPI can search a fault-tolerant task trajectory that satisfi es the requirements of the reachability and the overall kinematics performance of the manipulator simultaneously.The fault treatment strategy and fault-tolerant path planning method proposed in this paper can be extended to other space manipulators.Moreover,the proposed method can also be used to design the optimal configuration of manipulators.

Acknowledgements

This study was co-supported by the National Nature Science Foundation of China(No.’s 61403038 and 61573066)and theNationalBasicResearch Program ofChina(No.2013CB733000).