Direction finding for two-dimensional incoherently distributed sources with Hadamard shift invariance in non-uniform orthogonal arrays

Zhengliang DAI,Weijia CUI,Daming WANG,Bin BA,Chao WANG,Yankui ZHANG

National Digital Switching System Engineering&Technological Research Center,Zhengzhou 450001,China

KEYWORDS Array signal processing;Cramer-Rao lower bound;Direction-of-Arrival(DOA)estimation;Hadamard rotational invariance;Incoherently distributed sources;Non-uniform orthogonal array

AbstractThis paper proposes a novel algorithm for Two-Dimensional(2D)central Directionof-Arrival(DOA)estimation of incoherently distributed sources.In particular,an orthogonal array structure consisting of two Non-uniform Linear Arrays(NLAs)is considered.Based onfirst-order Taylor series approximation,the Generalized Array Manifold(GAM)model can first be established to separate the central DOAs from the original array manifold.Then,the Hadamard rotational invariance relationships inside the GAMs of two NLAs are identified.With the aid of such relationships,the central elevation and azimuth DOAs can be estimated through a search-free polynomial rooting method.Additionally,a simple parameter pairing of the estimated 2D angular parameters is also accomplished via the Hadamard rotational invariance relationship inside the GAM of the whole array.A secondary but important result is a derivation of closed-form expressions of the Cramer-Rao lower bound.The simulation results show that the proposed algorithm can achieve a remarkably higher precision at less complexity increment compared with the existing low-complexity methods,which benefits from the larger array aperture of the NLAs.Moreover,it requires no priori information about the angular distributed function.

1.Introduction

In most applications of array processing,Direction-of-Arrival(DOA)estimation methods are based on point source modeling,where the majority of energy transmitted by each source is considered from one single angle.1–3However,in real surroundings,especially in sonar,radar,and wireless communications,diffusion and multipath propagation around the vicinity of a source may cause angular spread of the source energy.4,5In this case,a distributed source model would be more appropriate.Depending on the correlation among different rays,distributed sources can be viewed either as Coherently Distributed(CD)sources or Incoherently Distributed(ID)sources.6More precisely,the source is called CD sources if the signal components arriving from different rays are replicas of the same signal,whereas in the ID sources case,all signals coming from different rays are completely uncorrelated.Throughout this paper,we concentrate on the central DOA estimation of ID sources.

In recent years,several techniques have been proposed for estimating the angular parameters of ID sources,such as Dispersed Parameter Estimator(DISPARE)algorithm,7Total Least Square Estimation Parameter Via Rotational Invariance Techniques(TLS-ESPRIT)algorithm,8Maximum Likelihood(ML)algorithm9,10and Covariance Matching Estimator(COMET)algorithm.11,12All the methods mentioned above are mainly developed for One-Dimensional(1D)localization of ID source model.Nevertheless,in lots of practical applications,signal and receiving array are not generally in the same plane,which corresponds to Two-Dimensional(2D)ID source model.A 2D ID source is characterized by four angular parameters:the central azimuth DOA,the azimuth angular spread,the central elevation DOA and the elevation angular spread.Despite the fact that there are some conventional optimum or near optimal methods for 1-D scenarios that can be extended to 2D scenarios,9–13all these methods suffer from heavy computationalburden due to multi-dimensional searches.

On the other hand,more recently,some low-complexity estimation algorithms involving the approximate signal models have been proposed for 2D central DOAs estimation of ID sources.Specially,the authors in Ref.14decoupled the 2-D nominal DOAs by Taylor series approximation using a pair of Uniform Circular Arrays(UCAs).Then,by combining the TLS-ESPRIT and Generalized Multiple Signal Classification(GMUSIC)method,the central elevation and azimuth DOAs could be estimated through 1D search.Similarly with Ref.14,using two parallel Uniform Linear Arrays(ULAs),the authors of Ref.15estimated the central elevation DOA based on TLS-ESPRIT,and meanwhile the central azimuth DOA was estimated by a Capon method instead of the GMUSIC method.Although avoiding multi-dimensional searches,the methods proposed in Refs.14,15both need 1D search and thus their computational complexities are still quite high.In orderto avoid spectralsearching,Ref.16proposed an ESPRIT-based approach for 2D DOA estimation of multiple ID sources employing a large uniform rectangular array.Making use of the linear relations among the array response matrices of the different sub-arrays,the central elevation and azimuth DOAs were both estimated based on the TLSESPRIT without spectral searching.

All the aforementioned low-complexity techniques impose constraints on the sensor spacing,which is limited to a halfwavelength strictly.Hence,they can be only used with uniformly-spaced array whose spacing has to be restricted within a half-wavelength.However,in practice,some of the sensors in a uniform array may stop functioning,which yields a non-uniform array.17Moreover,another application of the non-uniform arrays is the design of high performance and low cost arrays with reduced number of sensors.Reducing the number of sensors can effectively decrease the production cost as well as the computational time.So far,several DOA estimation algorithms based on non-uniform arrays have been proposed.17–20Nevertheless,the methods in Refs.17–19are based on the point source model.Only Ref.20proposed an angular parameter estimation method of ID sources via generalized shift invariance in arbitrary line arrays,which was limited to the 1D ID source model.To the best of our knowledge,using non-uniform arrays for the parameter estimation of 2D ID sources has not been reported.On the other hand,the orthogonal array is a commonly used 2D array geometry.Compared to other 2D arrays such as the uniform circular array and plane rectangular array,the orthogonal array can provide a larger aperture and hence offer better resolution for a given number of elements.In addition,the orthogonal array consists of two intersecting linear arrays working independently,and thus the computational complexity is only double that of a single dimensional array.

In this paper,our work is to extend the method in Ref.20to the 2D DOA estimation case.It is the first time that we introduce the non-uniform orthogonal arrays to estimate the 2D central DOAs estimation of ID sources.The central elevation and azimuth DOAs are obtained by employing a polynomialroot-based search-free approach.Then the parameter matching of the estimated 2D angular parameters is accomplished by searching the maximums of the cost function.Meanwhile,the Cramer-Rao Lower Bound(CRLB)is also derived regarding the 2D DOA estimation of the ID source.The proposed algorithm can achieve a remarkably higher precision at less complexity increment compared to the existing lowcomplexity algorithms,which benefits from the larger array aperture of the non-uniform arrays.Moreover,it performs independently of the angular distributed functions.

Notations:The superscripts (?)?,(?)Tand (?)Hstand for the conjugate,transpose and conjugate transpose operations,respectively.The notations C and R denote the complex number field and real number field,respectively.Ipis the p?p identity matrix,and 0p?qis p?q zero matrix.The symbols?,d(?) and diagf?g denote the Schur-Hadamard product,Kronecker delta function and diagonalization operation,respectively;Ef?g,det(?) and arg(?) represent the mathematical expectation,determinant and phase,respectively;minf?g and maxf?g stand for the minimum value and maximum value,respectively.

This paper is organized as follows.In Section 2,a detailed description of the signal model is presented.The derivation of the proposed algorithm is expounded in Section 3.In Section 4,the analysis of the proposed algorithm is presented.In Section5,some numericalexamples to illustrate the performance of the proposed algorithm are provided.Finally,conclusions are drawn in Section 6.

2.Signal model

It is assumed that there are K far-field narrowband ID sources impinging on the plane orthogonal array presented in Fig.1.The array geometry consists of two Non-uniform Linear Arrays(NLAs)Xaand Yalocated in the X?Y plane,which are composed of Mxand MyOmni-directional antenna elements,respectively.Letanddenote the position coordinates of elements along the x-axes and y-axes,respectively.Then the output signal vectors of the two NLAs Xaand Yaat time t can be expressed as14–16

Fig.1Geometry of orthogonal array considered.

where t=1;2;:::;T is the sampling time,and T is the total number of snapshots;sk(t) is the complex-valued signal transmitted by the kth source,and Lkis the number of multipath of the kth source;ck;l(t),hk;l(t) and uk;l(t) are the path gain,the azimuth DOA,and the elevation DOA of the lth path from the kth source,respectively.ne(t) is assumed to be a white Gaussian noise vector with zero mean and variance r2n.Moreover,ae(hk;l(t);uk;l(t)) is the array steering vector of NLAs Xaand Ya,

where

where k is the wavelength of the coming signal;xmandare the coordinates of the mth sensor in the NLAs Xaand Ya,respectively.

The azimuth DOA hk;l(t) and elevation DOA uk;l(t) can be expressed as

where hkand ukare the central azimuth DOA and the centralelevation DOA of the kth source;additionally, andare the corresponding small random angular deviations with zero mean and variancesand

In thispaper,thefollowing initialassumptionsare considered.

(1)The path gains ck;l(t),k=1;2;...;K,l= 1;2;...;Lk,t=1;2;...;T,are assumed as temporally independent and Identically Distributed(i.i.d.)Gaussian random variables,whose covariance is

3.Proposed algorithm

3.1.GAM modeling

In case of small angular spreads,the array steering vectormay be expressed by the Taylor series expansion as

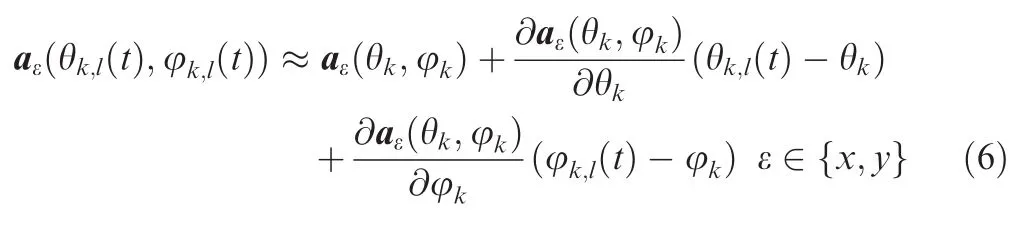
Define the random variables a0k,ahkand aukas follows:

and the output signal vectorin Eq.(1)can be approximately rewritten as

According to Eq.(2)it is easy to find the following linear relations between

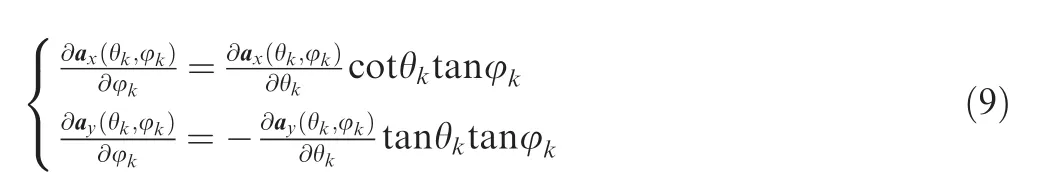
Therefore,we can reformulate Eq.(8)into the GAM model as

Note that the central DOAs have been separated from the original array manifold through GAM modeling.Since the transmitted signals and the noise are uncorrelated from each other,the covariance matrix of the output signal vectoris expressed as

where the diagonal matricesconsist of the 2K largest and the Me?2K smallest eigenvalues of,respectively.is the signal subspace matrix which corresponds to the 2K largest eigenvalues of.Whenis of full rank,also spans the column space of the GAM matrix,which yields

In practice,the sample covariance matrix may be estimated as

3.2.Central elevation and azimuth DOAs estimation

Let us divide the entire NLA Xainto two different sub-arrays Xa1and Xa2with equivalent number of sensors.To make full use of the received signal,the two sub-arrays are allowed to have overlapping sensors,and the number of sensors in each sub-array is.The first sub-array contains the sensors with coordinates,while the second sub-array contains the sensors with coordinatesFor simplicity,let us re-denoteas the locations of the sensors in each sub-array,respectively.Similarly,we also choose the first and last Ny=My?1 sensors of the NLA Yaas sub-array Ya1and Ya2,whose coordinates are re-denoted asrespectively.

The output signal vectors of sub-arrays Xa1,Xa2,Ya1and Ya2can be expressed separately as

By combining Eqs.(2)and(17),we can establish the following Hadamard shift invariance relationships between the GAMs of sub-arrays Xa1,Xa2and sub-arrays Ya1,Ya2,respectively,

where

Note that the sensors of the sub-arrays Xa1and Ya1cannot be located at the original in order to ensure a non-zero denominator in qen.Moreover,in order to avoid phase ambiguity,the minimal sensor spaceof the two NLAs should be less than k=2.

where Uy1and Uy2are composed by the firstand the lastrows of Uy,respectively.

Define a diagonal matrix as

where

According to the Hadamard rotational invariance relationships in Eq.(18),we can formulate a matrix F(ge)(e 2 fx;yg),

However,estimator Eq.(25)still requires computationally intensive spectral-peak searching.In order to reduce the complexity,we can derive a polynomial rooting approach when the array configuration conditions are determined.

Furthermore,Eq.(24)can be expressed as

Therefore,the denominator of Eq.(25)can be rewritten as the following polynomial:

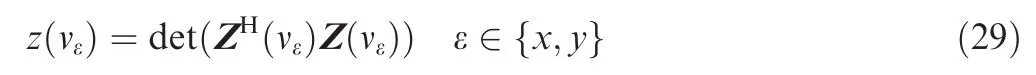
It is obvious that the central 2-D DOAs can be obtained by rooting this polynomial Eq.(29)and selecting the K roots closest to the unit circlesimilar to the traditional root-MUSIC estimator.21

3.3.Parameter matching method

Based on Taylor series approximation,we can also reformulate into the GAM model as

where

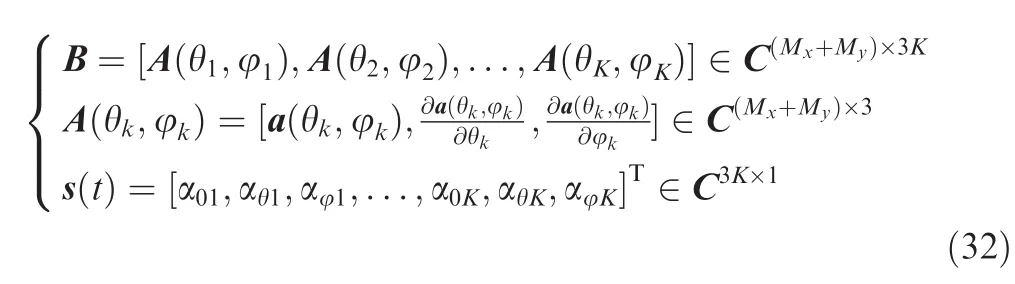
It is worth noting that there is also the Hadamard shift invariance relationship in the whole array,which is composed of two NLAs Xaand Ya.Hence,by defining two selection matrices

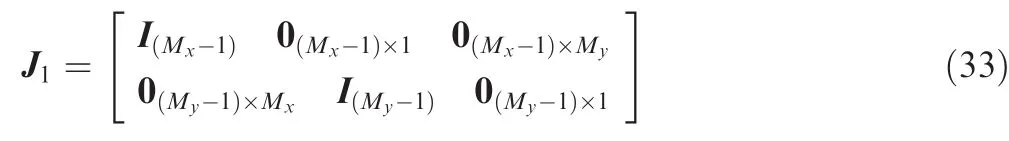
and

we can obtain

where

Let U be the signal subspace matrix of covariance matrixSimilarly,there is a unique non-singularmatrix T,which satisfies

Define a diagonal matrix as follows:

and we can also introduce a matrix F(gx;gy) which is written as

The pair-matching procedure is eventually accomplished by repeatedly maximizing Eq.(39)forThereafter,the estimated centralazimuth and elevation DOAscan be expressed as

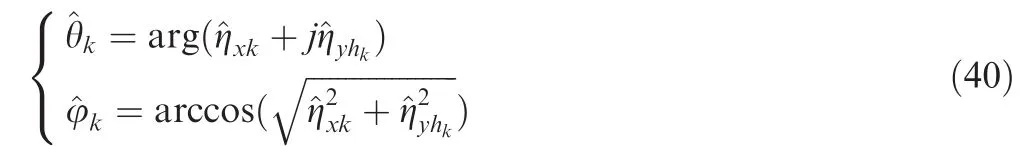
The procedure of the proposed algorithm can be summarized as follows:

Step 1.Calculate the sample covariance matrixwhere T is the total number of snapshots.Perform eigenvalue decomposition onandfind the signal subspace matrixcorresponding to the largest 2K eigenvalues.

Step3.Compute all the possible pairsfor the frequency parameter estimateCalculate the function valuesforEq.(39).The largest oneis the correct matching.

Step 4.Repeat the Step 3 for;...K to match all the parameters.

Step 5.Attain the estimates ofandforfrom Eq.(40).

4.Analysis of proposed algorithm

4.1.Complexity analysis

In this section,we analyze the computational complexity of the proposed algorithm compared with the GMUSIC algorithm in Ref.14and the 2D-ESPRIT algorithm in Ref.16.We assume that the sensor numbers of the two NLAs are both M.The main computational load of the proposed algorithm contains four operations:the estimation of the covariance matricesand R(thecalculated amountisaboutthe eigenvalue decomposition of these covariance matrices(the calculated amount is aboutthe rooting of the polyno mials(the calculated amount is aboutand the pair-matching procedure(the calculated amount is aboutIn above,the computational complexity of the proposed algorithm isMoreover,the main computational complexity of the GMUSIC algorithm and 2D-ESPRIT algorithm is given in Table 1(L denotes the number of searching points).

As the number of searching points L increases,it can be observed that the proposed algorithm provides lower computational complexity than the GMUSIC algorithm.In addition,the computational complexity of the proposed algorithm is slightly higher than that of the 2D-ESPRIT algorithm since the proposed algorithm does not require any spectrum searching.

4.2.Cramer-Rao lower bound(CRLB)

In this section,the CRLB for the 2-D central DOAs estimation of ID sources can be derived to measure the quality of the proposed estimator.We can rewrite the array steering vector of the whole array as follows:

For small angular spread,exploiting the spatial frequency approximation model,the covariance matrix R can be approximated and expressed as

in which

To derive the CRLB of the underlying estimation problem,let us denote a vector l containing all the central DOA parameters as

Table 1Complexity comparison.

Then,the vector-composed of all the unknown parameters is defined by

The CRLB of-can be computed from Ref.22

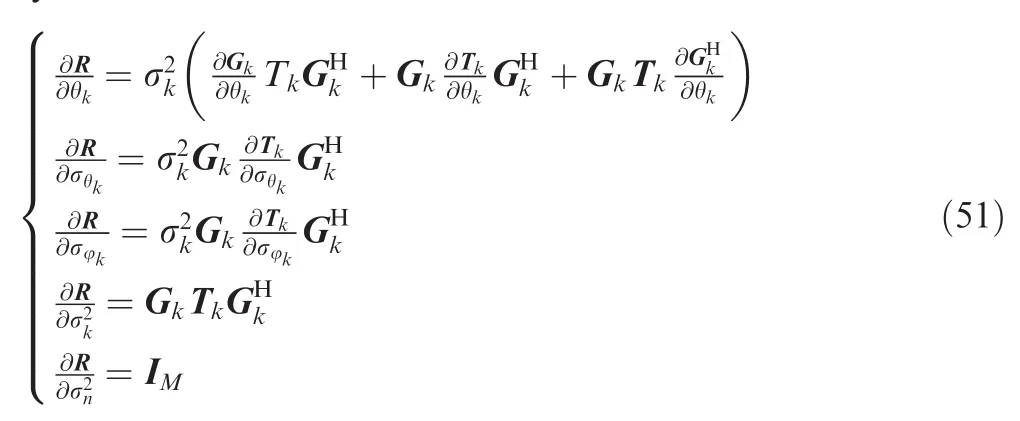
As we are interested to the CRLB of the 2-D central DOAs for the ID sources,we can use the inversion of block matrices to obtain the following expression of CRLB(l):

5.Simulation result and performance analysis

In this section,numerical results are shown to demonstrate the performance of the proposed algorithm.We consider an orthogonal array consisting of two NLAs.Each of the two NLAs was composed of 8 sensors and was placed in the X?Y plane.We assume that the sensors in the first array are placed atand the coordinates of the second array’s sensors are

It needs to be stressed that the algorithms in Refs.14,16are only suitable for uniform arrays and cannot be applied in non-uniform arrays.Therefore,the proposed method and other methods cannot use the same sensor array configuration because of the limitations of these algorithms themselves.In practical scene,the number of array elements is limited because a large number of array elements will lead to high hardware complexity,nevertheless the sensor spacing is easy to set and adjust.Thus it is reasonable to compare different algorithms under the same element number condition and the different sensor spacing.In addition,the variance of ray-gain is set as),and the number of scattering paths is set as).In the following every experiment,noise is a complex Gaussian process with zero mean and a total of 500 Monte Carlo runs for each trial were performed.For simplicity,the kth ID source is parameterized by the angular parameter vectorwhich determines the central azimuth,the azimuth angular spread,the central elevation,and the elevation angular spread,respectively.

We use the Root Mean Squared Error(RMSE)to evaluate the estimation performance,which is defined as

In the first experiment,we demonstrate the performance of the proposed algorithm under different angular distributed functions.The parameters of two ID sources areandThe numberof snapshots is set as T=500 and the Signal-to-Noise Ratio(SNR)is equal to 5 dB.We perform the algorithm in three cases:

Case 1.The two sources exhibit both uniform distribution.

Case 2.The two sources exhibit both Gaussian distribution.

Case 3.The first source exhibits uniform distribution,whereas the second source exhibits Gaussian distribution.For 50 independent trials,the central DOA estimates of ID sources are plotted in Fig.2(Note that Fig.2(a),(b)and(c)correspond to the three cases mentioned above,respectively).It can be seen that the proposed algorithm performs well for cases where the ID source has different deterministic angular distributed function.Thus the proposed algorithm performs independently of the angular distributed function.

Inthesecondexample,theperformanceoftheproposedestimatoraswellasacomparisonwiththeGMUSICalgorithmand 2D-ESPRIT algorithm are presented.The CRLB is also displayed as a benchmark.The arrays in GMUSIC algorithm and 2D-ESPRIT algorithm are both composed of 16 sensors.The parameters of two Gaussian shaped ID sources areThe RMSE curves of central elevation DOA estimations and central azimuth DOA estimations versus SNR are shown in Fig.3,respectively.It can be seen that the proposed algorithm has better estimation accuracy compared with the other algorithms.It is because there is a larger array aperture in the NLA than in the ULA when having the same number of sensors.

In the third experiment,we vary the number of snapshots and show the RMSEs of the proposed algorithm with other algorithms.The SNR is fixed at 5 dB and the other parameters are the same as these in the second experiment.The corresponding numerical results for central elevation DOA estimations and central azimuth DOA estimations are shown in Fig.4,respectively.We could see that when the number of snapshots increases,the RMSEs of the proposed algorithm degrade.In addition,the estimation accuracy of the proposed algorithm outperforms that of other algorithms for the central elevation and azimuth DOAs estimation.

Fig.3RMSE curves of central elevation and central azimuth DOA estimates versus SNR.

In the last experiment,we present the estimation performance of the proposed algorithm compared with other algorithms versus the angular spread in Fig.5.The angular spread varies from 1?to 10?.We set SNR=20 dB and the angular distribution is Gaussian function.The other parameters are the same as the second experiment.From Fig.5,it can be observed that with the increase of the angular spread,the estimation performance of the three algorithms deteriorates generally since the Taylor series approximation may introduce a larger error when the angular spreads are large.

Fig.4RMSE curves of central elevation and azimuth DOA estimates versus number of snapshots.

Fig.5RMSE curves of central elevation and azimuth DOA estimates versus angular spread.

6.Conclusions

(1)We consider the 2D central DOA estimation of ID sources in the non-uniform orthogonal array.Based on Taylor series approximation,the Hadamard shift invariance relationships inside the GAMs are established in the two NLAs.On the basis of such relationships,the central elevation and azimuth DOAs can be estimated by means of polynomial rooting method.Meanwhile,thepair-matchingmethod isalso presented.

(2)It is worth noting that the proposed algorithm is aimed at the 2D DOA estimation of ID sources using non-uniform arrays,whose array aperture will be enlarged when the same element number is used compared with the uniform array.Therefore,the proposed algorithm can reach a remarkably higher precision at less complexity increment compared to the existing low-complexity algorithms,which benefits from the larger array aperture of the NLAs.

(3)Moreover,the proposed algorithm performs independently of the angular distributed functions.

Acknowledgement

This study was supported by the National Natural Science Foundation of China(No.61401513).

Appendix A.We can assume thatand) are zero-mean random variables with probability density functionMoreover,is generally assumed as a symmetric function inand.

In this paper,we consider two typical distributions ofThey are uniform shape

and Gaussian shape

respectively.