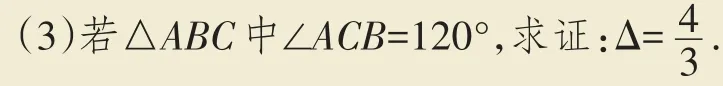当抛物线“遇上”等边三角形

江苏省海安市城南实验中学九（3）班

二次函数的图像是抛物线，常常有一些特殊图形与它相伴.最近经常做到一类抛物线与等边三角形的综合题，深入钻研之后，我发现了一个有趣的性质，这里记录出来，与大家分享一下.

例题平面直角坐标系xOy中，顶点为C的抛物线y=ax2+bx+c与x轴交于A，B点（点A在点B左边）.若△ABC为等边三角形，求证：b2-4ac=12.

图1

解答思路：可以先画出图1进行草图分析（设a＞0，抛物线开口向上），△ABC为等边三角形时，想到作出CH⊥AB于点H，根据特殊的“边角关系”可得CH=AB.这时CH与抛物线顶点C的纵坐标有关，重点把AB的长也表示出来就行了.考虑到抛物线y=ax2+bx+c与x轴（即直线y=0）交于A，B点，则点A，B的横坐标对应着关于x的一元二次方程ax2+bx+c=0的两根.再表示出抛物线顶点C的坐标，作出CH⊥AB于H，则等腰三角形ABC底边上的高CH就是

走向一般：如图2，平面直角坐标系xOy中，顶点为C的抛物线y=ax2+bx+c与直线y=n交于A，B点.若△ABC为等边三角形，是否仍然有b2-4ac=12？

图2

思路探究：此时对应的方程是抛物线y=ax2+bx+c与直线y=n联立得到的关于x的一元二次方程ax2+bx+c-n=0.关于x的一元二次方程可算出AB的长为线顶点C的坐标出CH⊥AB于H，则等边三角形ABC底边上的高

知道了抛物线的内接等边三角形对应着“Δ=12”这个性质，对有些习题的解答是十分方便的，比如我遇到的下面的这道题：

习题二次函数y=ax2+bx+1（a≠0）的图像与x轴有两个交点A，B，顶点是C.若△ABC恰好是等边三角形，则代数式b2-2（2a-3）的值为_______.

解答：把代数式b2-2（2a-3）展开整理，得到b2-4a+6，再对照二次函数表达式中常数项c=1，即待求式子转化为b2-4ac+6，结合△ABC恰好是等边三角形，可得Δ=12，于是代数式b2-2（2a-3）的值为18.

同学们，我总结的“这一招”，你们学会了吗？

教师点评

曹姝同学这篇数学写作质量很高，达到“数学小论文”的级别，其对抛物线“内接等边三角形”的探究不只是对图形关系的研究，而是挖掘特殊三角形与抛物线解析式中系数的对应关系，而且有“走向一般”的深度拓展，也体现了“以形助数”“以数驭形”的数学思想.受到她“走向一般”的启发，我们还可以进一步“扩大成果”，把与之相关的同类问题再做一些梳理.在例题的图形中，适当变式，还可提出以下问题：

（1）若△ABC为直角三角形，则△ABC为等腰直角三角形，有AB=2CH，

（2）若△ABC中∠ACB=120°，有AB=23·CH，

我们把“它们”都列到一起：平面直角坐标系xOy中，顶点为C的抛物线y=ax2+bx+c与x轴交于A，B点（点A在点B左边）.

（1）若△ABC为直角三角形，求证：Δ=4.

（2）若△ABC为等边三角形，求证：Δ=12.