预应力混凝土箱梁温度梯度荷载下的应力研究

2018-12-25王绍平

交通科技 2018年6期

王绍平

(无锡市政设计研究院有限公司无锡 214072)

大量调查与研究表明，箱梁桥中裂缝的出现并非都是由直接荷载作用引起的，还有可能是由温度、收缩徐变等变形作用引起[1]。由于混凝土的热传导性差，混凝土桥梁在日照、气温等气象条件作用下，会产生非线性温度梯度，当所产生的温度变形受到约束时，便会出现较大的温度应力[2]。在混凝土连续刚构箱梁桥中，温度应力可达到甚至超过活载应力，应力过大可能会引起结构开裂，影响到结构耐久性。国内外众多研究表明，日照、气温及其他气象因素在桥梁内引起的温度应力是造成桥梁破坏的主要原因[3]。因此，在桥梁具体的设计和施工过程中必须重视温度效应的影响。

大部分学者都是基于实桥的温度监测数据拟合出适用于该地区的温度梯度[4]，较少考虑在气象因素作用下的最大温度梯度。本文基于某座已完工预应力混凝土变截面连续刚构箱梁桥，采用有限元法对箱梁温度场进行研究，并计算最大竖向正温度梯度。同时运用有限元通用程序midas Civil对实测、理论和规范竖向正温度梯度下的温度应力进行计算分析，比较不同正温度梯度对混凝土箱梁温度应力的影响，为该地区混凝土箱梁桥的温度应力计算提供参考。

1 竖向温度梯度取值研究

箱梁竖向温度梯度作用效应在箱梁温度作用中占主导地位，因此，国内外桥梁设计规范在考虑混凝土箱梁的温度梯度时，一般只考虑竖向温度梯度，忽略沿桥梁纵向长度方向的温度变化，即把复杂的三维问题转化为一维问题来考虑。我国JTG D60-2015 《公路桥涵设计通用规范》(以下简称《公路桥规》)给出混凝土上部结构的双折线竖向温度梯度，并规定全国采用相同的温度梯度值，然而我国地域辽阔，气象环境复杂多样，这种统一的取值方法是否具有普适性还有待验证。本节通过实测、有限元分析和规范计算3种方法确定3种形式的竖向正温度梯度取值。

1.1 实桥观测竖向正温度梯度

某预应力混凝土变截面连续刚构箱梁桥跨径为72 m+130 m+72 m，桥墩与主梁固结，跨中横截面构造见图1。主梁采用C60混凝土，桥面铺装为10 cm厚沥青混凝土。于2016年8月16日对该桥的跨中截面进行温度观测研究，温度传感器布置见图2。

图1 箱梁跨中横截面构造图(单位：cm)

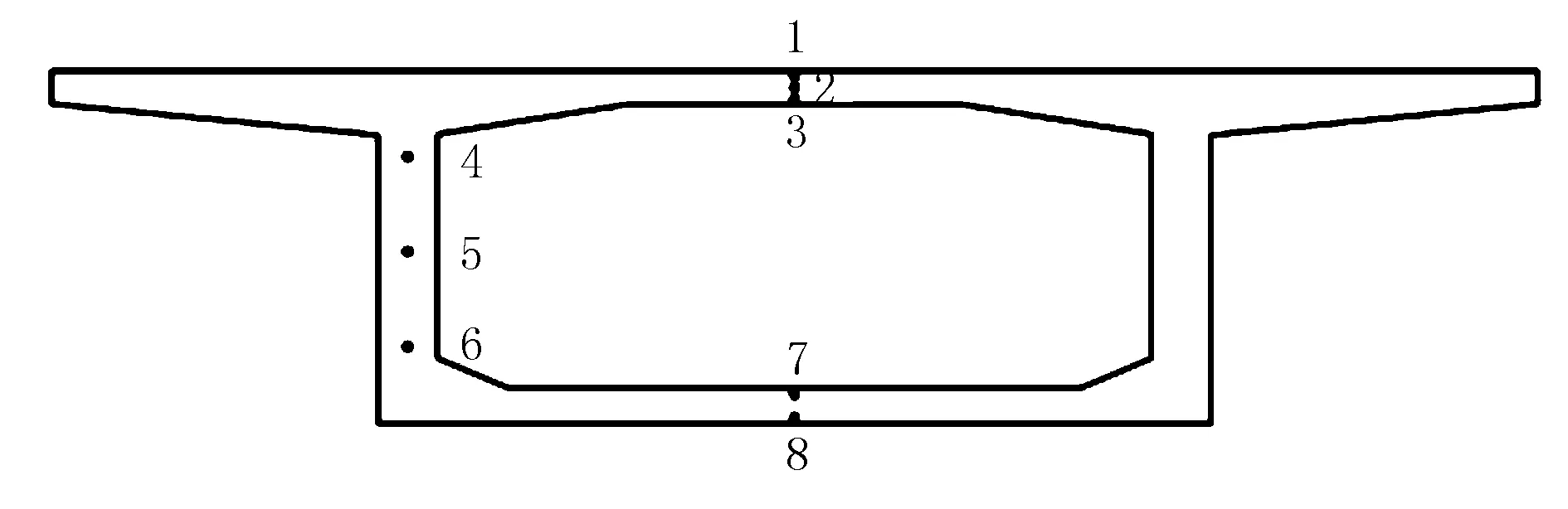
图2 跨中截面测点布置图

对所观测数据进行研究，各测点温度变化曲线见图3。

图3 跨中截面测点温度

由图3可见，顶板和底板上下缘最大温差分别为10.1 ℃和-2.8 ℃；腹板沿梁高方向基本不存在温差。

根据我国铁路桥梁规范的指数函数曲线拟合公式Ty=T0e-ay，并结合最小二乘法对顶板和底板沿梁高方向的最大正温差曲线进行拟合，得到该桥的实测正温度梯度，见图4。

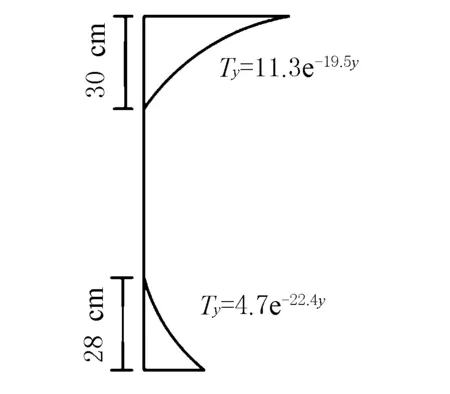
图4 实测竖向正温度梯度

1.2 理论最大竖向正温度梯度

基于气象因素的有限元法模拟混凝土箱梁的温度场具有较高精度[5]。考虑理论最大太阳辐射强度、最高大气温度作用等气象因素，利用midas FEA建立箱梁最不利温度场，并计算理论竖向正温度梯度。其中，最大太阳辐射强度考虑发生于6月21日，按Ångström-Page模型和Hottel模型计算[6]，最高大气温度根据统计分析结果取为41.7 ℃，按正弦函数进行模拟[7]。最大太阳辐射强度和最高大气温度计算结果见图5。

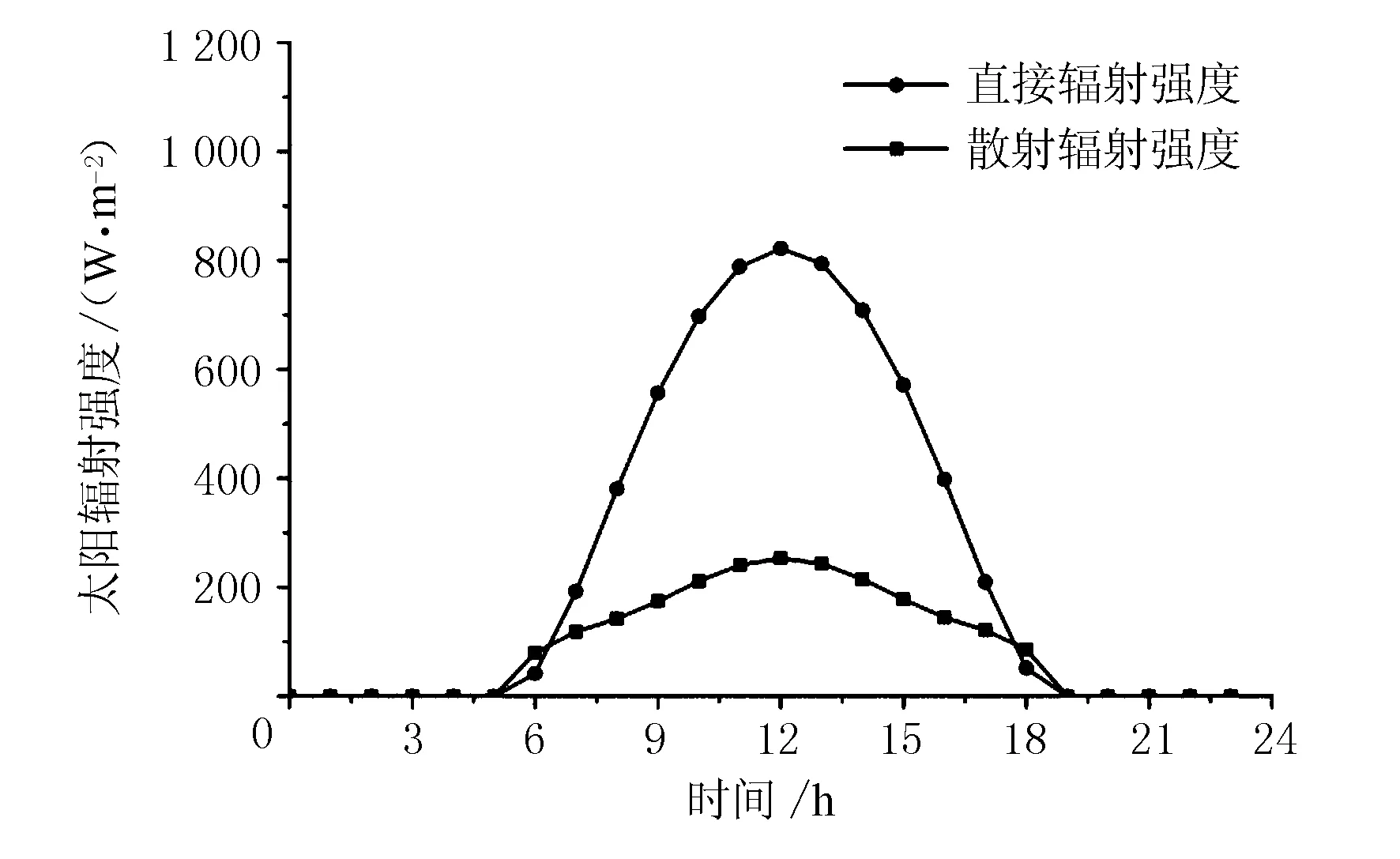
a) 最大太阳辐射强度计算值

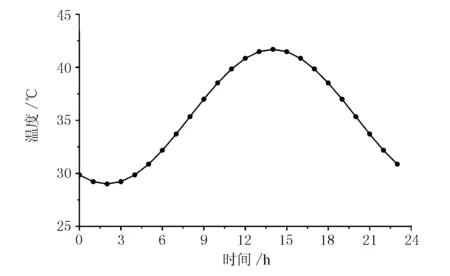
b) 日最高温变化曲线

根据图1的箱梁跨中截面尺寸建立有限元模型，将热辐射、热对流和太阳辐射按第三类边界条件施加在有限元模型上，箱梁内温度考虑为大气温度，太阳辐射强度和大气温度按图5取值。风速取为1.0 m/s。混凝土和沥青材料的热物理参数[8]按表1取值。单元选用2D平面应变单元，网格划分尺寸为0.02 m，全截面共划分27 059个节点，25 944个单元，平面有限元模型见图6。根据有限元计算结果并结合指数函数曲线拟合公式得到的理论竖向正温度梯度见图7。

表1 模型材料热物理性质

图6 跨中截面有限元模型

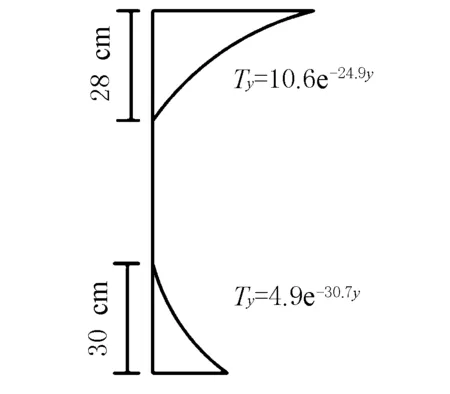
图7 理论竖向正温度梯度

1.3 《公路桥规》竖向正温度梯度

《公路桥规》通过对各国温度梯度计算原理的对比研究，最终参照美国AASHTO桥梁规范，对桥梁结构由于梯度温度引起的效应作了较为详细的规定。图8为《公路桥规》规定的竖向正温度梯度曲线，本文桥面板为100 mm沥青混凝土铺装层，因此表面的最高温度T1为14 ℃，T2为5.5 ℃。

对混凝土结构，当梁高H<400 mm时，图8中A=H-100(mm)；梁高H≥400 mm时，A=300 mm。t为混凝土桥面板的厚度，mm。

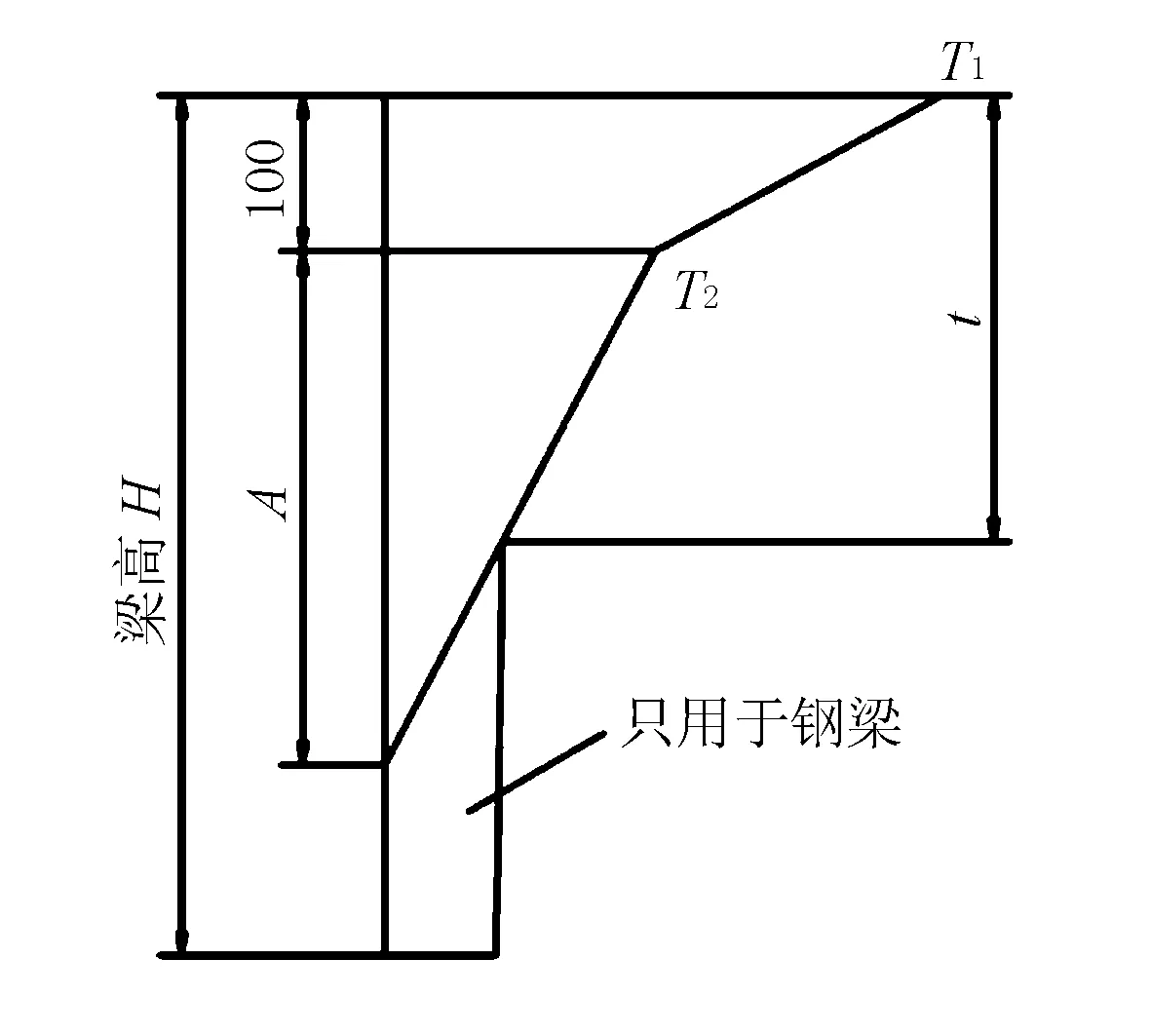
图8 竖向正温度梯度(单位：mm)

2 温度效应对比分析

根据上述确定的3种箱梁竖向正温度梯度，采用midas Civil比较混凝土箱梁在不同竖向正温度梯度下温度效应，确定竖向正温度梯度取值的合理性。

2.1 有限元模型

采用midas Civil空间梁单元建立全桥成桥阶段模型，混凝土强度等级为C60，桥墩与主梁的固结作用采用弹性连接中刚接模拟。边跨支座采用一般支承，全桥共划分318个单元，323个节点，有限元模型见图9。模型荷载主要考虑沿梁高方向的温差分布，采用梁截面温度荷载加载。分别选取图4、图7和图8共3种温度梯度进行成桥阶段上部箱梁的温度效应分析。

图9 混凝土箱梁温度效应计算模型

2.2 挠曲变形分析

在正温度梯度作用下，箱梁顶板温度高于底板温度，因此，顶板要向两侧变形，由于受到纵向约束作用，将发生挠曲变形，使得梁体两边跨向上挠曲而中跨向下挠曲。3种温度梯度下各跨跨中挠曲变形见表2。

表2 各跨跨中挠曲变形 mm

由表2可见，3种温度梯度作用下的挠曲变形规律相同，都是两边跨向上挠曲而中跨向下挠曲。实测和理论温度梯度得到的挠曲幅度区别不大，而规范温度梯度得到的挠曲幅度大于实测和理论正温度梯度作用，说明规范温度梯度对于挠曲变形的考虑略显保守。

2.3 纵向应力分析

在超静定的连续刚构箱梁桥中，非线性的温度梯度不但会引起箱梁桥的位移，而且多余约束的存在还会使结构产生温度次应力。取中跨为研究对象，桥墩和跨中的上下缘温度应力结果见图10。其中正号为拉应力，负号为压应力。

图10 混凝土箱梁截面应力对比

由图10a)可见，箱梁顶板上缘主要受压应力作用，实测和理论温度梯度得到的上缘应力区别不大，而规范温度梯度得到的上缘应力大于实测和理论温度梯度作用，为1.2倍左右。这是由于桥墩与主梁固结对主梁纵向变形有阻碍作用，使桥墩和跨中顶板上缘主要受压，且温度应力变化不大。

由图10b)可见，实测和理论正温度梯度得到的下缘应力在桥墩和跨中都是受压，而规范正温度梯度为下缘受拉。这主要是由于是否考虑底板正温差引起的，由于规范温度梯度不考虑底板正温差，故仅在顶板正温差作用下顶板受压而底板受拉。但实际桥梁中由于底板正温差的存在，使顶板受拉而底板受压，且在底板产生的压应力大于顶板正温差在底板产生的拉应力，因此，实测和理论正温度梯度得到的下缘应力在桥墩和跨中都表现为受压。此外规范正温度梯度计算得到的跨中截面下缘拉应力为1.3 MPa，已达到混凝土抗拉强度设计值的50%，但实际桥梁由于底板温差的存在，截面下缘实际受压，不会因为抗拉强度不足而产生裂缝，因此规范对于截面下缘应力的考虑较为保守。

从以上分析可知，实测和理论正温度梯度计算得到的挠曲变形和纵向应力区别不大，因此对于某地区的预应力混凝土箱梁的温度应力计算，在缺乏实测数据时，可以采用理论正温度梯度进行考虑。规范正温度梯度计算得到的挠曲变形和纵向应力相比实测正温度梯度要略显保守。