城市曲线匝道桥地震响应分析及延性抗震设计
2018-12-25游云川冯振兴
游云川 冯振兴
(中铁二院工程集团有限责任公司 成都 610031)
对于桥梁抗震设计,一般采用以下2种策略:延性设计和减隔震设计。延性设计是指预先设定某些构件(一般为桥墩)在罕遇地震作用下进入弹塑性阶段以耗散地震能量,而其他构件均处于弹性状态。其核心内容是如何保证预想指定的构件发生损伤,并且这些构件既有足够的耗能能力,又不会发生脆性破坏[1]。减隔震设计是指利用减隔震装置以达到延长结构周期、耗散地震能量、降低结构响应的目的。其核心内容是设计合理、可靠的减隔震装置并使其在结构抗震中充分发挥作用,而结构其他构件的响应为弹性[2]。
目前对桥梁设计来说,采取恰当的减隔震装置,保证桥梁构件处于弹性状态无疑是较为简便的,但后期需对其进行定期的检查和维护,增加养护工作量,且减隔震装置的费用较高,对场地及结构的要求均比较高,因而从该角度,延性设计较减隔震设计具有一定的优势。
本文以兰州市雁青互通一匝道桥曲线梁桥为工程背景,采用多阵型反应谱法对其进行弹塑性地震响应分析,并依据城市桥梁抗震设计规范对其进行延性抗震设计。
1 工程概况
雁青互通式立交属于兰州市二环路的重要组成部分,与T605号路通过东岗立交连接北环路和南山路而贯通成环状道路。本文研究对象为其C匝道上的1联预应力混凝土连续曲线箱梁桥,平曲线半径R=100 m,孔跨布置为29.5 m+36 m+29.5 m,上部结构采用支架现浇预应力混凝土箱梁,单箱单室截面,箱宽10.4 m,梁高1.9 m,下部结构采用单柱花瓶墩,墩梁固结体系,墩底为2.8 m×1.6 m矩形截面,桩基采用直径1.5 m圆形截面。桥址区地震动峰值加速度值为0.20g,地震动反应谱特征周期0.45 s,抗震设防烈度为9度。
全桥总体布置见图1。

图1 P10~P13联桥型布置立面图(单位:cm)
2 分析模型的建立
2.1 曲线匝道桥建模要点
正确地建立桥梁结构的动力空间模型是进行桥梁抗震分析的基础,对于曲线梁桥,有限元建模时应注意以下几点[3-4]。
1) 主梁模拟。上部结构的质量必须尽可能地模拟准确,一般不采用复杂的实体单元或板壳单元,采用能反映上部结构质量分布和刚度特征的简化骨架(梁)单元来模拟,单元的划分宜尽量精细。二恒荷载和横隔梁质量以附加质量或换算密度的方式计入梁体结构中。
2) 支座模拟。在有限元软件中,对于普通钢支座可采用刚性连接模拟,对于橡胶支座可采用输入一定刚度值的弹性连接模拟。有限元模拟时应根据主梁平面线形,旋转连接坐标系,以使其与实际支承方向一致。
3) 桥墩模拟。为准确反映实际桥梁结构的动力特性,要求每个墩柱至少采用3个杆系单元,且需对桥墩单元进行旋转,使其方向与实际布置情况一致。
4) 基础弹性刚度模拟。桩与土相互作用效应采用纵横向土弹簧模拟,弹簧刚度根据土层的m值进行计算。
本桥上下部均采用梁单元模拟,墩梁固结处采用刚性连接模拟,支座采用一般弹性连接模拟,基础桩土效应采用节点弹性支承模拟,模型建立完成见图2。

图2 全桥有限元分析模型
2.2 地震动参数的选取
地震动输入是计算桥梁结构地震响应的依据,桥梁结构的地震分析,一般以地震地面运动作为地震动输入。在地震地面运动特性中,对结构破坏有重要影响的因素主要有地震动强度、频率谱特性和强震持续时间,因此,在选择地震动输入时,必须使这3个方面的特性都满足要求。
目前对于曲线梁桥,地震动输入的常用方法有旋转激励法和规范规定的沿桥墩连线方向和垂直连线方向的多方向地震动输入法。根据相关研究,2种计算方法得到的桥墩最大地震反应基本接近[5]。
本文按照《公路桥梁抗震设计细则》规定的多方向地震输入法进行研究,计算中地震激励为:不考虑竖向振动影响,水平激励方向分成2种类型,即本联两端连线方向(顺桥向)和垂直于割线方向(横桥向)。反应谱形式为
式中:Tg为特征周期;η2为结构的阻尼调整系数;γ为自特征周期至5倍特征周期区段曲线衰减指数;η1为自5倍特征周期至6 s区段直线下降段下降斜率调整系数;Smax为水平设计加速度反应谱最大值。
Smax=2.25A
式中:A为E1或E2地震作用下水平向地震峰值加速度。
本工程为位于VIII(0.2g)度区的乙类桥梁,E1时Ci取为0.61,E2时Ci取为2.0。模型中输入的地震加速度反应谱见图3。
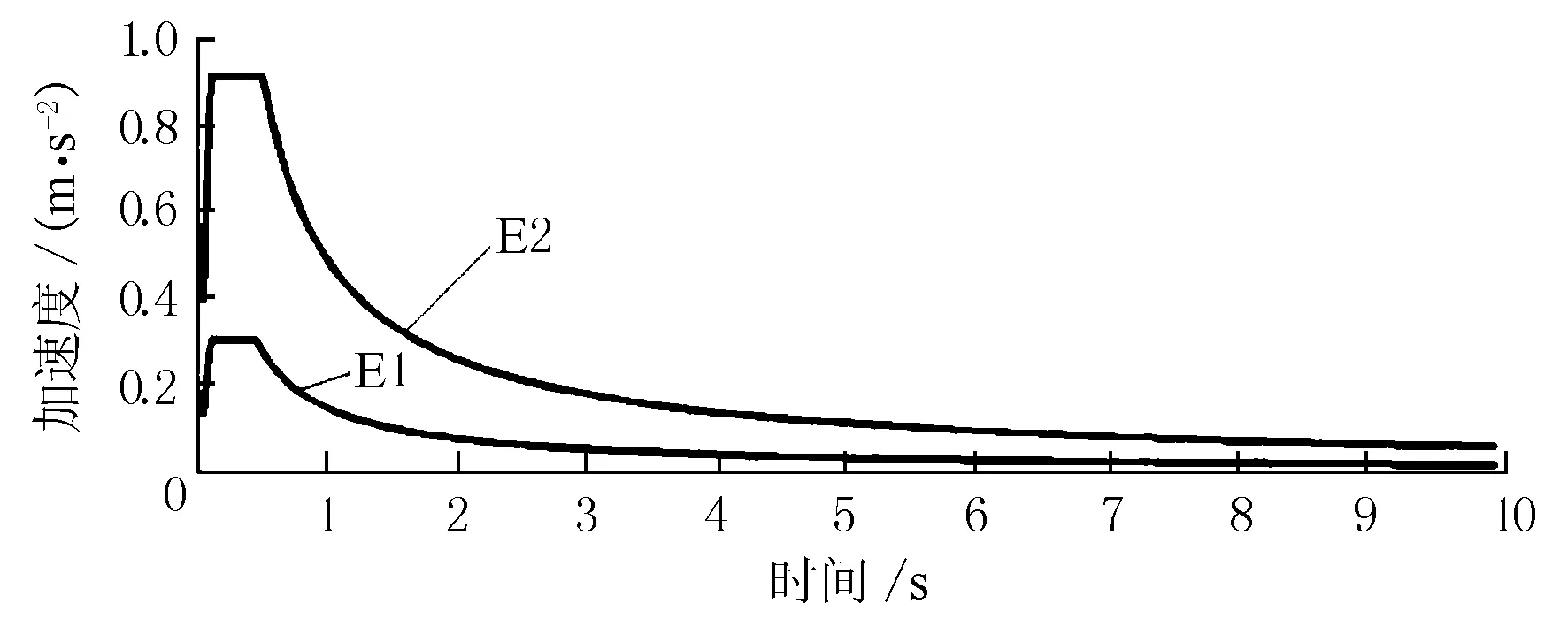
图3 设计加速度反应谱
2.3 分析方法
本桥平曲线半径仅为100 m,小于20倍桥面宽度,为不规则桥梁。按规范规定采用A类设计方法的非规则桥梁,在E1和E2地震作用下其分析方法均可采用多阵型反应谱法或非线性时程方法,故本桥设计时在E1和E2地震作用下均按多阵型反应谱法进行分析,计算模型中取参与计算振型为前100阶,振型组合方法采用CQC法,该方法考虑了频率接近时的阵型相关性,计算精度较高,计算结果可信。
3 能力保护设计原则
能力保护设计原则的基本思想在于:通过设计,使结构体系中的延性构件和能力保护构件形成强度等级差异,确保结构构件不发生脆性的破坏模式。对桥梁来说,一般选择墩柱作为延性构件,而墩柱抗剪能力、盖梁、结点,以及基础均按能力保护构件设计,其设计弯矩、设计剪力和设计轴力均为墩柱的极限弯矩所对应的弯矩、剪力和轴力[6],因此,延性设计构件的截面尺寸及配筋成为控制设计的关键。截面尺寸过大、配筋过强易造成能力保护构件难以设计,造成材料的浪费;截面尺寸偏小、配筋偏弱又易造成墩柱在E1作用下不满足弹性要求或E2作用下变形过大。
本桥桥墩为单柱花瓶墩,塑性铰设置在墩底,设计时分别对3.2 m×1.6 m,3.0 m×1.6 m,2.8 m×1.6 m,2.6 m×1.6 m 4种墩柱截面尺寸及不同的配筋形式进行了分析研究,最终选择2.8 m×1.6 m作为最终墩柱截面尺寸设计方案。
4 分析结果
4.1 动力特性分析结果
表1列出了结构振动前5阶的周期。

表1 结构动力特性
4.2 E1地震作用下弹性分析
E1地震荷载作用最不利组合下的单柱墩底内力值见表2。

表2 E1地震荷载最不利组合下的单柱墩底内力
本桥为VIII度区上的乙类桥梁,依据城市桥梁抗震规范规定,采用A类抗震设计方法设计。在E1地震作用下,根据规范验算桥墩及基础的强度。
截面的抗弯强度通过截面的(P-M)分析得到,采用Ucfyber软件计算,截面约束混凝土的应力-应变本构关系采用Mander模型,钢筋本构关系采用考虑强化段的双折线模型。典型截面的P-M曲线见图4。

图4 墩底截面的P-M曲线
验算结果表明,E1地震下桥墩及基础的强度满足要求,满足规范规定的乙类桥梁E1地震作用下的性能目标:立即使用,结构总体反应在弹性范围内,基本无损伤。
4.3 E2地震作用下塑性分析
截面弯矩-曲率(M-φ)分析是确定构件临界截面曲率延性能力的基本分析工具。对箍筋约束混凝土桥墩,通过截面弯矩-曲率分析,可以从理论上确定其塑性铰区域截面的曲率延性系数,还可以进一步确定桥墩墩身塑性铰区截面的位移延性系数。典型截面的M-φ曲线见图5。

图5 墩底截面M - φ曲线
截面塑性转角验算结果见表3。

表3 表格截面塑性转角验算
注:K为延性安全系数,取2.0。
由于墩顶横桥向未进入塑性状态,可不进行截面塑性转角验算,由表3可见,桥墩其余各截面塑性转角均能满足要求。
4.4 能力保护构件设计
如前所述,墩柱塑性铰区域斜截面抗剪能力及基础均按能力保护构件设计,其内力设计值为墩柱的极限弯矩所对应的内力值,并考虑了截面超强系数的影响。限于篇幅,本文仅列出桥墩塑性铰区域斜截面抗剪验算见表4,其余能力保护构件亦能满足设计要求。

表4 塑性铰区域斜截面抗剪强度验算
5 结语
本文以一城市曲线匝道桥为工程背景,采用多阵型反应谱法对其进行了地震作用下的弹塑性分析,并根据规范及能力保护设计原则评估了桥墩的抗震性能。结果表明,该桥墩的延性设计可以满足既定的设计目标,即“小震不坏,大震不倒”,且大震时桥墩屈服,能力保护构件仍处于弹性状态。
