基于MEA模型的作战飞机装备保障需求研究

陈 博，徐常凯，杜加刚

（勤务学院航材四站系，江苏 徐州221000）

随着部队战斗力的不断提升与发展，航空兵部队参加演习作战任务越来越频繁，后勤保障部队的保障压力也越来越大，不断担负各种各样的作战保障任务，在作战任务中某一项备件不能够正常使用都可能会导致飞机发生因缺件而停飞的现象，使航空兵部队的作战效能大大降低，对整场演习作战任务产生不良影响。现在大多数研究集中与对平时的作战装备消耗预测上，由于在作战条件下的影响因素复杂，不确定因素大，所以对于作战装备预测消耗研究相对较少，且采用的一般神经网络、灰色系统等算法都具有一定的鲁棒性，预测结果易陷入局部最优解，难以准确地把握装备的消耗预测水平，本文结合保障经验与相关文献，对作战装备保障的消耗影响因素进行深入分析，并在此基础上，对基于思维进化算法的作战飞机可修件保障需求量确定的求解步骤进行详细介绍。

1 装备消耗数量预测影响因素分析

携行装备的消耗数量受不同种类的影响因素的制约，与此同时，这些不同种类的因子对消耗量的影响程度也各不相同，通过数据的统计与分析，可将影响携行器材消耗数量的因素分为四大类[1]，包括任务因素、装备的可靠性因素、人为因素以及地理环境因素。

（1）任务因素

不同种类的任务模式对携行装备消耗数量的影响可谓千差万别，例如在航空兵进行空中进攻作战时，其装备的消耗量较大，进行防御作战时作战装备消耗数量相对较小，对于任务的影响程度可以采用飞机的出动强度、起落架次以及空中作战时间等参数进行量化[2]，其根据具体执行任务情况而定。

（2）携行装备的可靠性水平

携行装备的可靠性水平主要是指作战装备在一定时间内、在一定条件下无故障地执行指定功能的能力或可能性[2]。可通过可靠度、失效率、平均无故障间隔等来评价携行装备的可靠性，在此基础上考虑保障任务的实际情况，包括执行任务飞机上的装备的装机时间以及历史任务的消耗数据。装备装机时间主要是指在执行任务时飞机上的装备的工作情况，对于装机时间长的装备其剩余寿命较短，所以在预测时其需求量很可能需要增加。据统计战时装备故障率λ（t）根据装备类型的不同而服从三种不同的分布包括指数分布、正态分布以及威布尔分布[3]，通过各分部服从的概率分布密度以及可靠度的计算，可以表示出各类部件的故障率，服从不同分布的故障率函数的计算方法如下所示：

1）指数分布

根据保障经验故障率服从指数分布的装备约占携行装备的90%，大部分电子设备就属于这类分布，服从指数分布的装备其消耗特点主要具有无记忆性即在t时刻后，其发生故障率与t时刻之前的状态无关，其寿命长短不会缩短。为方便叙述，设携行装备第项器材（i=1，2，3，···n）服从指数分布，j为该项器材失效的次数，由此可计算出该项作战器材的故障率[4]：

其中n表示单个装备上该项器材的安装的数量，1/λ表示第i项作战装备的平均故障间隔时间（MTBF），t为该项作战装备的实际使用时间，N表示在作战任务中的总失效次数。

2）正态分布

携行装备保障中装备寿命服从正态分布的分布函数器材发生第j次故障的概率为：

其中μ为器材寿命均值，可用于表示为第i项携行装备的平均故障间隔时间，σ为标准差，可由该项器材的长期保障数据经验得到，-∞＜t＜+∞；其可靠度函数为：

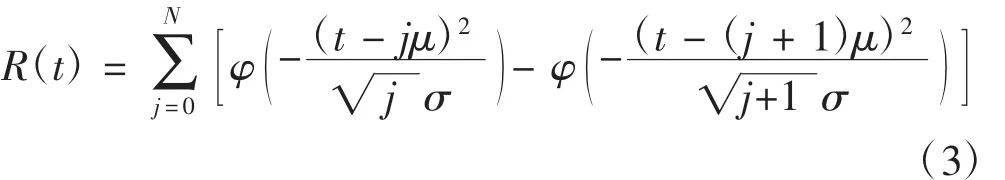
可以计算出服从正态分布的作战装备的故障率为：

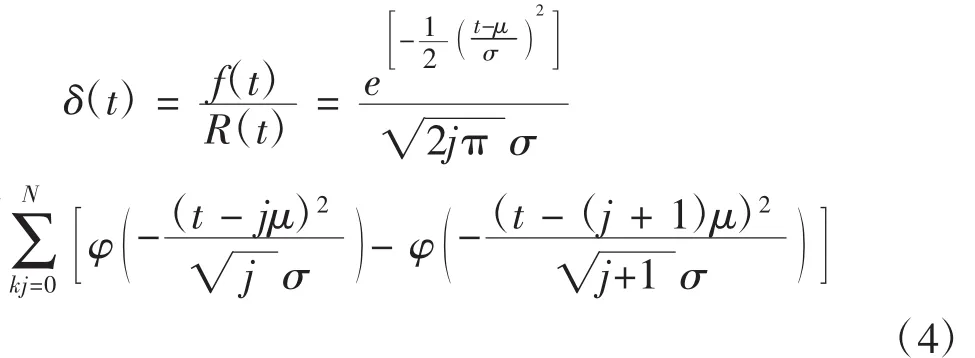
此类作战装备故障的产生原因是由于细微的器材消耗累积而成的，一般可用于计算非金属的常进行磨损的器材。

3）威布尔分布

威布尔分布主要适用于对部分不可修复类的携行器材的寿命分布函数进行拟合[5]，当第i项作战装备服从参数为（α，β）时，其概率密度函数以及分布函数为[6]：

其中α为形状参数；β为尺度参数；t≥0；其可靠度函数为：

可计算出服从威布尔分布的作战装备故障率函数为：

由上述可知通过输入执行某次任务的作战装备器材的相关参数即可得到计算出概念器材的故障率，例如假设不可修复器材A是故障率服从指数分布的电子类器材，单机安装数为2，其平均故障间隔时间为300 h，已经使用18 h，在某次作战任务中飞机的空中战斗时间为8 h，通过公式可计算出器材A发生第2次故障的故障率为：

（3）人员因素

在某些任务环境下，由于装备保障条件较为恶劣，人为的因素对携行装备消耗的影响更大，装备保障工作人员的保障水平就是其中一项非常重要的影响因素，装备保障人员在进行装备保障的过程中对器材的收发是否符合规范流程、对器材的管理是否按照业务规范、对器材的封装保管是否细致正确，这都将影响携行装备的消耗量，特别是在特殊的任务环境下，对保障业务越熟悉制定的保障计划以及处理应急的时间就越合理，携行装备需求量就越小。

（4）地理环境因素

地理环境主要是指装备保障部队在执行保障任务过程中所处地形、气候、温湿度等自然环境因素，其对携行器材的消耗数量的影响也是十分巨大的，例如在高原地区因其空气稀薄、温度低、昼夜温差变化剧烈、风沙灰尘较多、紫外线强烈等原因使液压系统、装备气源、电气、动力系统等航空设备的消耗量增加；与此同时，相关研究表明温湿度的急剧变化或者过高、过低对通信设备会产生一定的不良影响。按照以上原则并根据相关文献[7]进行的层次分析法，对不同属性的携行装备和地形地貌进行分类，并依据其属性对其受环境的影响程度进行量化，量化结果如表1.

表1 环境对携行装备消耗的影响因素量化

2 基于MEA算法的可修备件需求预测模型

在对作战装备消耗的各影响因素进行分析的基础上，本文采用思维进化算法来进行优化，思维进化算法（MEA）是在传统的种群算法的基础上发展形成的启发式搜索算法，其主要是在一定的约束范围内通过不断的迭代，找到对于目标函数的最优值。

思维进化算法采用了遗传算法的相关概念包括“种群”、“个体”、“环境”等概念并在此基础上进一步细分，设立全局公告板用来实现各种群之间信息的交流，设立局部公告板记录子种群的进化过程，其具体过程包括：

（1）网络初始化

由于思维进化算法沿用了遗传算法的群体、进化等概念，因此网络初始化部分基本相同，这里可以借鉴遗传算法的网络初始化部分内容。

（2）子群体生成

根据适应度函数计算个体适应度值，得分最高的前M个个体选定为优胜个体，（M+1）～（M+N）个个体作为临时个体，以优胜个体和临时个体为中心，分别生成M个优胜子群体和N个临时子群体。

（3）趋同操作

各子群体内部个体进行局部竞争转变为胜者的过程，竞争过程持续到子群体成熟，即不再产生新的胜者，此时的子群体得分为最优个体的得分，并将结果粘贴到全局公告板上，直到所有子群体成熟，趋同工作才结束。

（4）异化操作

成熟子群体之间为成为胜者而进行的全局竞争，从全局公告板上比较优胜子群体和临时子群体得分，通过得分筛选出全局最优个体。异化结束后，计算最优个体适应度值，判断是否满足迭代次数和精度要求，不满足则返回网络重新进行（2）～（3）步操作。进化结束后解码最优个体作为网络结构初始权值和阈值，本文中模型的建立和运算在Matlab环境中进行。思维进化算法的优化过程如图1所示[8]。

图1 思维进化算法流程图

算法初始先随机选取n个群体，并根据设置的函数计算各群体对应的分数，再在此基础上对数据进行趋同和异化的操作，本文将某次作战飞机消耗器材分为为N个。按照正态分布随机抽取Nj个种群，追求经济的最小化，从而确定出Y个优胜子群体和P个临时子群体，在此基础上对各个子种群进行趋同操作进行种群迁徙，迁徙策略公式为：

其中Ωi（t）为t时刻种群的行为；δi（t）为其相应的变化量；In（t）为其包含信息的浓度；Fbi（t）表示在整个种群搜索的结果；hbi（t）表示某个种群在寻优过程中的结果；c1与c2表示学习因子；r1和r2表示之间的随机数；ϖ为惯性权重。由此可以进一步挑选出优胜种群，并在此基础上进行变异操作，将成熟子群体作为中心点进行搜索，产生新的种群，并根据评级函数与之前的种群进行竞争，再按照约束条件判断在此备件需求预测的情况下，是否能够保证飞机可用度达到标准，最终输出作战飞机器材配置数据。

3 算例分析

本文在上述算法分析的基础上，收集作战飞机的装备保障的相关数据，结合部队的具体保障实际，对算法中的参数进行具体的假设，并在此基础上进行计算检验，证明算法的有效性与合理性。

本文通过Matlab软件实现对作战装备消耗数量预测的思维进化神经网络组合模型[9]，并对预测出的结果进行分析，选取空军某一歼10飞机装备保障部队在执行过去10次转场保障任务中的某项携行器材的消耗数量，首先取前5组数据作为训练数据对思维进化算法神经网络进行训练，剩余5组作为测试集对训练出的模型阈值进行测试，网络共进化学习100次，部分数据如表2所示。

表2 携行装备的各项影响因素预测消耗数据

先将数据进行思维进化优化，再将其带入到神经网路中进行优化计算，根据算法输入端与输出端的个数，设置中间层的节点数，其参数具体设置如表3.

表3 参数设置表

最终完成网络训练，其优胜子种群的趋同过程如图2所示。

图2 优胜子种群优化

其临时子种群的趋同优化过程如图3所示。

图3 临时子种群优化

最终选出得分最高的种群，得到该次任务该项器材最优的消耗预测数量，与实际任务的平均误差为1.168 3%，具体数值如表3所示。

表3 不同任务的器材消耗数量

4 结语

作战飞机装备保障需求预测是作战备件供应保障的重要内容。本文首先对各作战飞机装备消耗的影响因素进行的深入分析，并在此基础上，充分构建初始种群然后通过思维进化算法进行优化，最后通过具体算例进行实现，结果表明该方法能够实现在一定条件下装备需求预测功能且精度较高，有很好的实用价值，对于增加飞机备件保障的军事效益与经济效益具有重要意义。