10 000箱大型集装箱船典型货舱结构极限强度

滕 蓓，管义锋，祁恩荣，顾根南，咸 屹

(1. 江苏省无锡交通高等职业技术学校，江苏 无锡 214151；2. 江苏科技大学，江苏 镇江 212003；3. 中国船舶科学研究中心，江苏 无锡 214082)

0 引 言

目前在船舶结构设计中，往往根据规范要求计算设计载荷，如静水弯矩和波浪弯矩。而评估航行船舶船体结构在设计载荷中的富余强度是考核船体梁能够承受总纵弯曲的极限承载能力。特别是10年内已经发生了2起大型集装箱船船体结构受损的重大事故，船体结构的极限强度评估方法也必须进一步完善。国际船级社协会就强化船舶结构安全标准的事项进行讨论，决定增加有关集装箱船总纵强度的UR-S11A条款及有关集装箱船功能要求与负载推荐的UR-S34条款，并于2016年7月1日生效。相比之下，UR-S11A在原先的UR-S11基础上提高了船体结构承受垂向波浪弯矩和垂向波浪剪力的设计要求，假如结构不做改进设计的话，船体梁的富余强度会大大减小，原先的船体结构极限承载能力可能都无法满足设计要求。

由于早年计算机不如现在发达，为了计算船体梁的极限强度，学者们可谓想尽了一切办法，Smith[1]在船体极限强度领域内做出了卓越的贡献，利用逐步弯曲破坏的过程来预报船体梁在垂向弯曲状态下的极限强度，并以他的名字命名为Smith简化方法。Yukio[2]提出一种理想结构单元法，可以大大减少计算时间。经过多年的研究，极限强度的计算方法得到不断发展和完善，特别是随着计算机的运算能力显著提高，商业有限元软件功能相当完善，利用有限元方法来求解极限强度相对容易解决，特别还能考虑材料弹塑性和几何大变形这种非线性行为，不管完整[3]还是受损[4–5]状态下的船体结构极限强度评估方法都已经逐步成熟。此外，针对液化天然气船的液舱围护系统[6–7]和超大型浮体模块间的连接器[8]也有相应的评价手段。目前Smith简化方法已经被最新的散货船、油船协调共同规范采用，而新生效的集装箱船总纵强度评估标准UR S11A也认为Smith简化方法和有限元法可以作为极限强度评估的较好手段。

和散货船、油船不同，集装箱船的显著特点是大开口，它在遭遇斜浪的时候货舱舱口很容易发生扭曲变形。在评估集装箱船的极限强度时，尽管按照规范要求只要评估船体梁的垂向弯曲极限承载能力，但是还是十分有必要来讨论货舱结构在水平弯曲情况下极限强度的特点，特别是当垂向弯矩和水平弯矩联合作用下的极限强度[9]。

本文选取1艘典型的10 000箱集装箱船，针对其货舱结构中横剖面内的主要纵向构件，分别采用基于逐步破坏法的MARS2000软件和非线性有限元Ansys软件，计算其结构的极限承载能力。

1 集装箱船船体结构极限承载能力评估方法

1.1 逐步破坏法

规范规定，船体梁的极限强度是船体结构相邻剖面在增加转角时结构所承受的垂向弯矩极值。

由于船体梁的极限强度具有弹塑性的特征，一般采用增量迭代法求解，通常认为：材料具有弹塑性特性；横剖面结构不因弯曲发生位移和翘曲；一般取强框架之间的所有主要纵向构件参与计算；横剖面结构划分成一系列加筋板单元。

根据每个加筋板单元的非线性应力-应变关系，采用增量迭代方法，在每个弯曲状态下各个离散单元的应力叠加后得到垂向弯矩，将这些离散值连成弯矩-弯曲曲率曲线，取极值即是极限弯矩。

增量迭代方法求解船体梁极限强度的主要步骤如下：

1）将集装箱船横剖面结构划分成加筋板单元；

2）根据受拉屈服、板筋交界屈服、加强筋侧倾、腹板屈曲、梁柱屈曲、板格屈曲等6种不同的失效模式分别定义加筋板单元的应力-应变关系；

3）给定初始曲率和水平中和轴的位置，初始垂向弯矩值为0；

4）增加剖面转动曲率，计算每个加筋板单元的应变，根据加筋板单元的应力-应变关系获得应力；

5）根据弯矩平衡方程，获得新的水平中和轴的位置；

6）根据新的水平中和轴计算应力并进行叠加，获得剖面新的垂向弯矩值；

7）与前一转角计算的垂向弯矩值相比，假如增大，则重复步骤4～步骤6，一旦出现降低，可确定垂向极限弯矩，即极限强度。

1.2 非线性有限元法

非线性有限元法分析极限强度是一种准静态的分析方法，其操作思路与逐步破坏法相类似，也是针对船体结构相邻剖面内的纵向构件进行逐步加载求解端面载荷。非线性有限元法不仅可以考虑非线性的几何变形、材料的应力应变关系，而且可以分析特定区域如某个舱段内的结构极限强度、复杂连接结构的极限强度，已经不受剖面保持平面的约束，能够展现更加符合实际的屈曲失效模式，还能考察后屈曲性能，加载方式更加灵活，既可以通过载荷加载，又可以通过位移加载，边界条件符合基本的简单支撑。

计算船体结构极限强度采用的有限元法，通常有以下步骤：

步骤1确定评估的舱段范围，对集装箱船来说，一般取强框架之间的所有主要纵向构件，如甲板板、船底板、船底内板、舷侧板、纵桁、纵骨等。

步骤2根据几何尺寸建立结构有限元模型，选定高阶具有弹塑性分析功能的单元，划分网格，设定约束条件，施加载荷，进行线弹性分析，根据应力结果确定结构进入屈服极限对应的载荷。

步骤3进行线性屈曲分析，提取第一阶扩展模态，乘以板格系数，加载到有限元结构模型上，这个几何位移条件作为初始缺陷。

步骤4根据弹塑性材料应力应变关系设定材料的塑性范围，加载2倍左右的结构进入屈服极限对应的载荷，开启几何大变形，设定初始步长，开始迭代求解，直到获得载荷位移端缩曲线。

2 集装箱船典型结构

本文选取1艘典型的10 000TEU大型集装箱船的中横剖面作为研究目标，该10 000箱集装箱船的主尺度见表1。

表1 10 000箱大型集装箱船主尺度Tab.1 Principal particulars of 10,000 TEU containership

该集装箱船的典型货舱区域中横剖面结构图如图1所示，目前集装箱船的板材和构件均采用高强度钢（弹性模量206 GPa，泊松比0.3）设计，根据屈服极限不同分为2种强度等级，分别是355 N/mm2和390 N/mm2。图中标注的AH，DH，EH是根据不同温度下达到的冲击韧性而分，而图中未标注型材材料的均为AH。

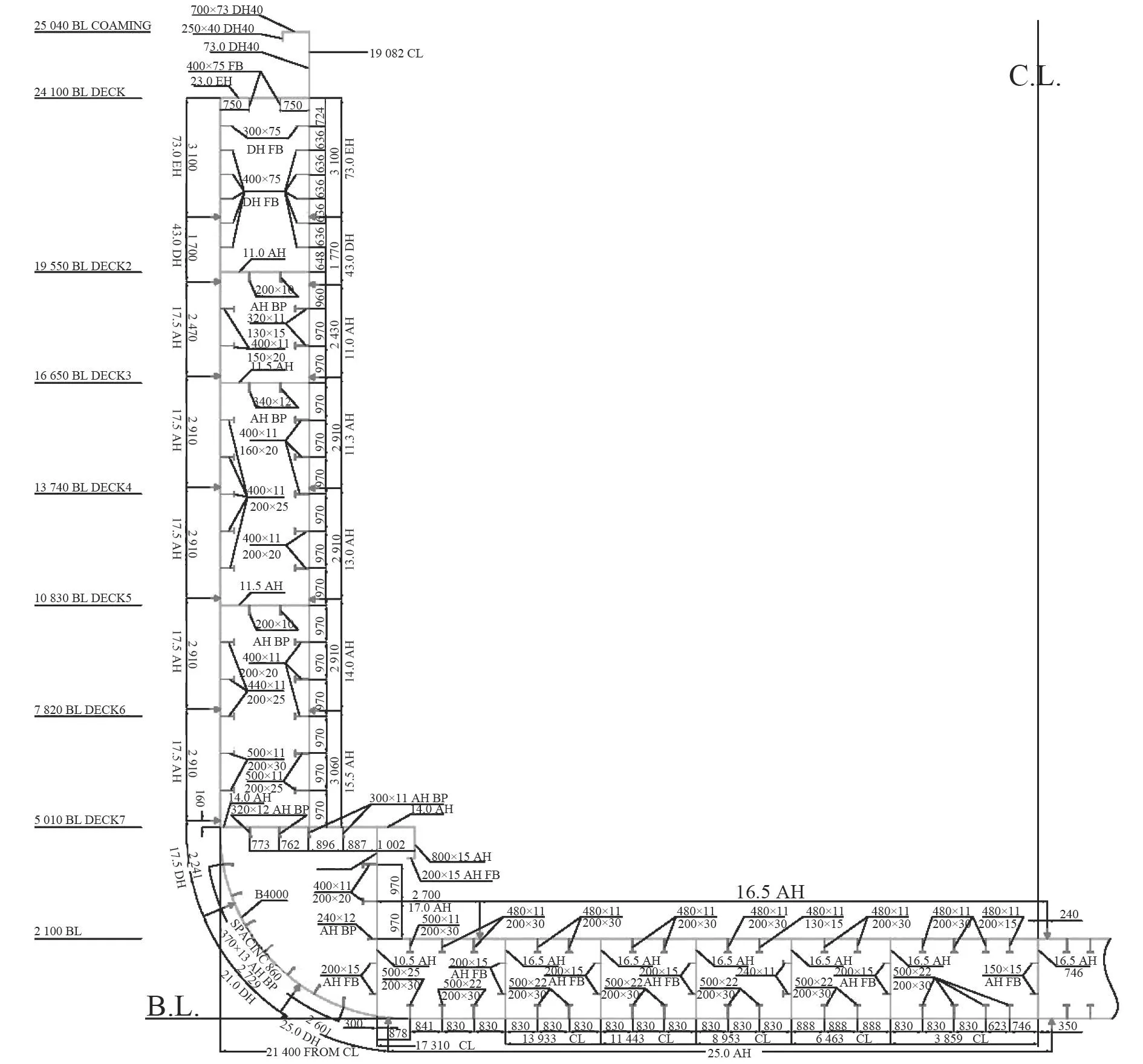
图1 10 000箱集装箱船典型货舱的中横剖面图Fig.1 Typical transverse section in the hold of 10 000 TEU containership

3 基于逐步破坏法的MARS2000软件计算结果

本文采用法国船级社的MARS2000软件计算了10 000箱集装箱船典型剖面的极限强度，MARS2000软件中建立的中横剖面模型如图2所示，包括主要纵向板材和纵向骨材，由于剖面的对称性只需建立右舷（或左舷）结构。

图2 MARS2000软件剖面模型Fig.2 Section model with longitudinal stiffnesses in MARS2000 software

该集装箱船的横剖面中拱和中垂极限强度曲线的计算结果如图3所示，中拱为正，中垂为负，这里曲线1代表水平弯矩，曲线2代表垂向弯矩，曲线3代表综合弯矩，由于综合弯矩中的水平弯矩分量为0，则垂向弯矩与综合弯矩重合。点划线4为该集装箱船的设计载荷。

图3 MARS2000软件垂向弯曲极限强度计算结果Fig.3 Ultimate strength of vertical bending moment in MARS2000 software

由于集装箱船在海洋中航行时不可避免出现水平弯矩，因此，按照水平弯曲与垂向弯曲的曲率比值，分别从0.1～1.0计算其水平弯曲和垂向弯曲联合作用下的极限强度值，图4 ～ 图7分别显示了该比值为0.2，0.4，0.6，0.8时的极限强度分布情况。

从图4～图7可以发现：

1）随着水平弯曲与垂向弯曲的曲率比值增加，水平极限弯矩不断增大，垂向极限弯矩不断减小。

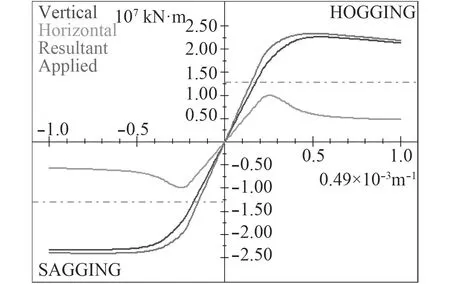
图4 MARS2000软件极限强度（水平弯曲与垂向弯曲的曲率比值为0.2）Fig.4 Ultimate strength in MARS2000 software (the horizontal/vertical curvatures ratio is 0.2)

图5 MARS2000软件极限强度（水平弯曲与垂向弯曲的曲率比值为0.4）Fig.5 Ultimate strength in MARS2000 software (the horizontal/vertical curvatures ratio is 0.4)

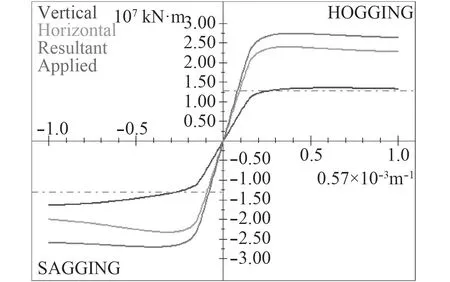
图6 MARS2000软件极限强度（水平弯曲与垂向弯曲的曲率比值为0.6）Fig.6 Ultimate strength in MARS2000 software (the horizontal/vertical curvatures ratio is 0.6)

图7 MARS2000软件极限强度（水平弯曲与垂向弯曲的曲率比值为0.8）Fig.7 Ultimate strength in MARS2000 software (the horizontal/vertical curvatures ratio is 0.8)

2）通过计算发现，水平弯曲与垂向弯曲的曲率比值在增加到一定值前，综合极限弯矩增加较为缓慢，垂向极限弯矩减小较为缓慢，是因为在这阶段主要由垂向极限弯矩贡献，水平极限弯矩的分量贡献小。而水平弯曲与垂向弯曲的曲率比值大于该值后，水平极限弯矩贡献增大，综合极限弯矩也相应增大，直至垂向弯曲为0时，综合极限弯矩完全和水平极限弯矩重合，即纯水平极限弯矩。

4 基于有限元法的Ansys软件计算结果

4.1 有限元模型及材料属性

本文采用通用型商业有限元软件Ansys，计算分析10 000箱集装箱船典型货舱区域中横剖面结构的极限强度。图8是该集装箱船左舷一侧的有限元模型，利用镜像功能将得到全宽范围的中横剖面结构，其中，板材采用SHELL181单元，纵向骨材选用BEAM188单元，单元长度取400 mm，共8 960个单元，7 883个节点。该集装箱船在货舱的舱口间纵向范围内可以放置2个20 ft的标准箱或者1个40 ft的长箱，货舱采用纵骨架式的形式，纵骨间距830 mm，每个舱口间有16档肋位，肋距为791 mm，每4档肋位设置1道横向强肋位，根据规范要求选取一个横向强肋位之间的主要纵向构件进行建模。

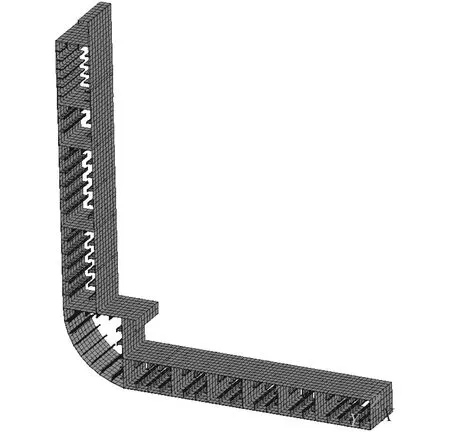
图8 Ansys软件有限元模型Fig.8 Finite element model in Ansys software

10 000箱集装箱船典型货舱结构中横剖面的主要纵向构件有2种强度的船用钢材，分别是屈服极限为390 MPa的H40和355 MPa的H36，通常情况，在没有试件试验数据的情况下，数值模拟计算时可以将材料的应力应变非线性关系简化成弹性理想塑性关系，即在Ansys软件中建立双线性等向强化材料（BISO），适用于各项同性材料大应变分析，这2种材料的弹性理想塑性关系，即应力-应变曲线如图9所示。

4.2 边界条件和加载方式

图9 材料应力应变曲线Fig.9 Stress versus strain curve

边界条件是有限元分析中最重要的部分，如果约束不够，方程会有多个解，假如约束太强，应力结果会偏大。本文按照规范的要求，取集装箱船典型货舱段中横剖面有限元模型的左端所有节点，施加固定约束，即约束了6个自由度的运动，如图10所示。

图10 边界约束Fig.10 Boundary constrains

计算有限元模型右端得中和轴的位置在距基线10.973 m处，并在船中建立参考点，将右端结构节点均与之刚性绑定，即在参考点施加载荷时，会将载荷全部传递给结构右端面所有节点，如图11所示。此外，在该参考点上约束水平位移UY、垂向位移UZ、扭转转角ROTX。对于施加载荷来说，在参考点既可以选择施加弯矩，又可以施加转角，本文采用施加转角的方式，中拱转角ROTY为0.001 rad，中垂转角ROTY为–0.001 rad，水平转角ROTZ为0.001 rad，而求相应的弯矩就是参考点的支反弯矩。

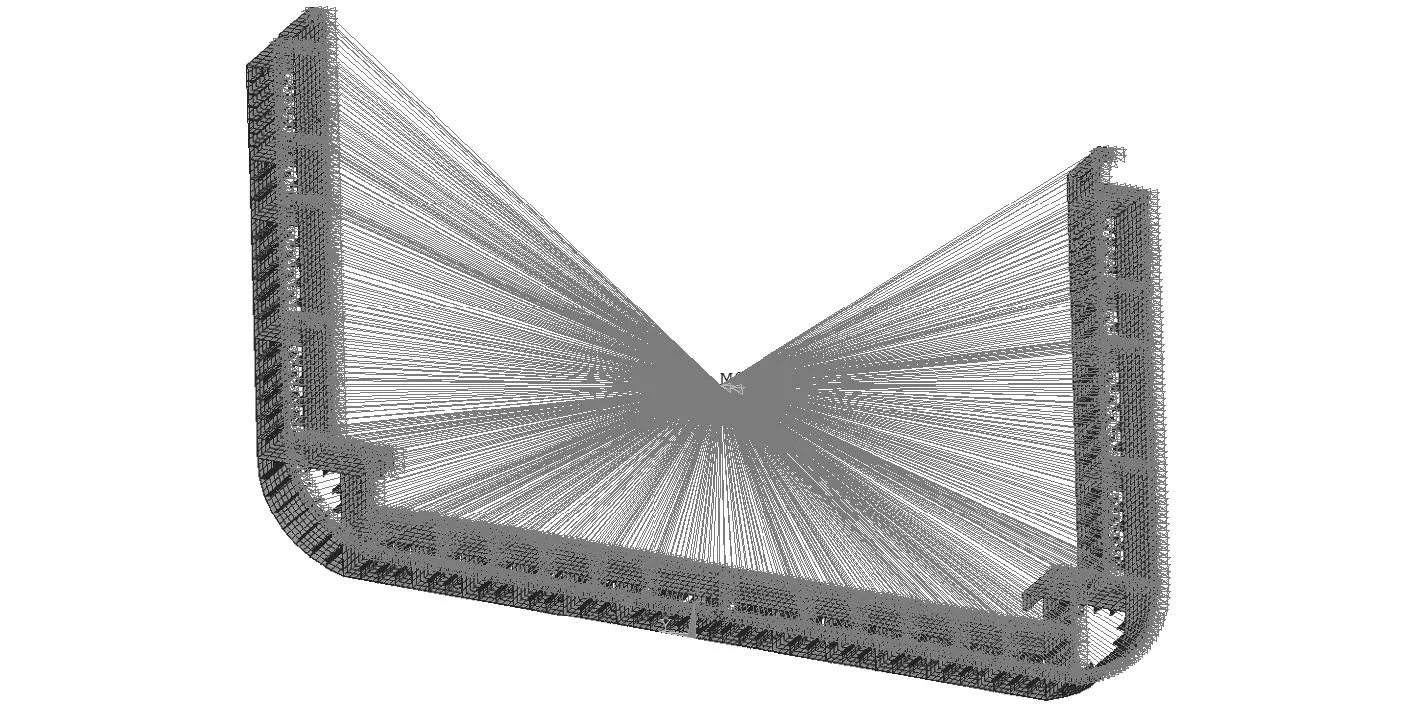
图11 加载方式Fig.11 Loads apply

4.3 非线性有限元计算结果

在非线性分析前需要加入初始变形或者初始缺陷，采用线性屈曲的分析方法，在经过线弹性分析后，利用子空间法求解并读取第一阶模态，乘上纵骨间距系数，叠加到原先结构上得到初始变形。

本文在非线性求解阶段采用弧长法，设置最大弧长为1，最小弧长为0.000 1，初始步长0.01，最终时间步为1，开启几何大变形。通过计算，获得了如图12的垂向弯矩-曲率曲线。根据该曲线，较容易知道集装箱船货舱结构在中拱状态和中垂状态下的极限强度。

图12 非线性有限元的垂向极限强度值Fig.12 Stress under the vertical ultimate moment

图13为中垂极限弯矩状态下的等效应力分布，图14为中拱极限弯矩状态下的等效应力分布。而单独计算水平极限弯矩状态下的等效应力分布如图15所示。

从图中可以清晰看出各个极限状态下集装箱船中横剖面结构的应力分布符合实际情况。在中垂极限状态下，船底板尚未屈服，但是二甲板附近已经出现屈曲，甲板及抗扭箱也发生塑性变形，水平中和轴略有上移；在中拱极限状态下，船底板受屈曲失效，同时甲板及抗扭箱也基本已经处于屈服状态，水平中和轴略有下移。在水平极限弯曲状态下，二甲板和三甲板的纵壁已经出现明显的屈曲，舷侧和舭部区域也明显已经进入塑性阶段，垂向中和轴未发生变化。

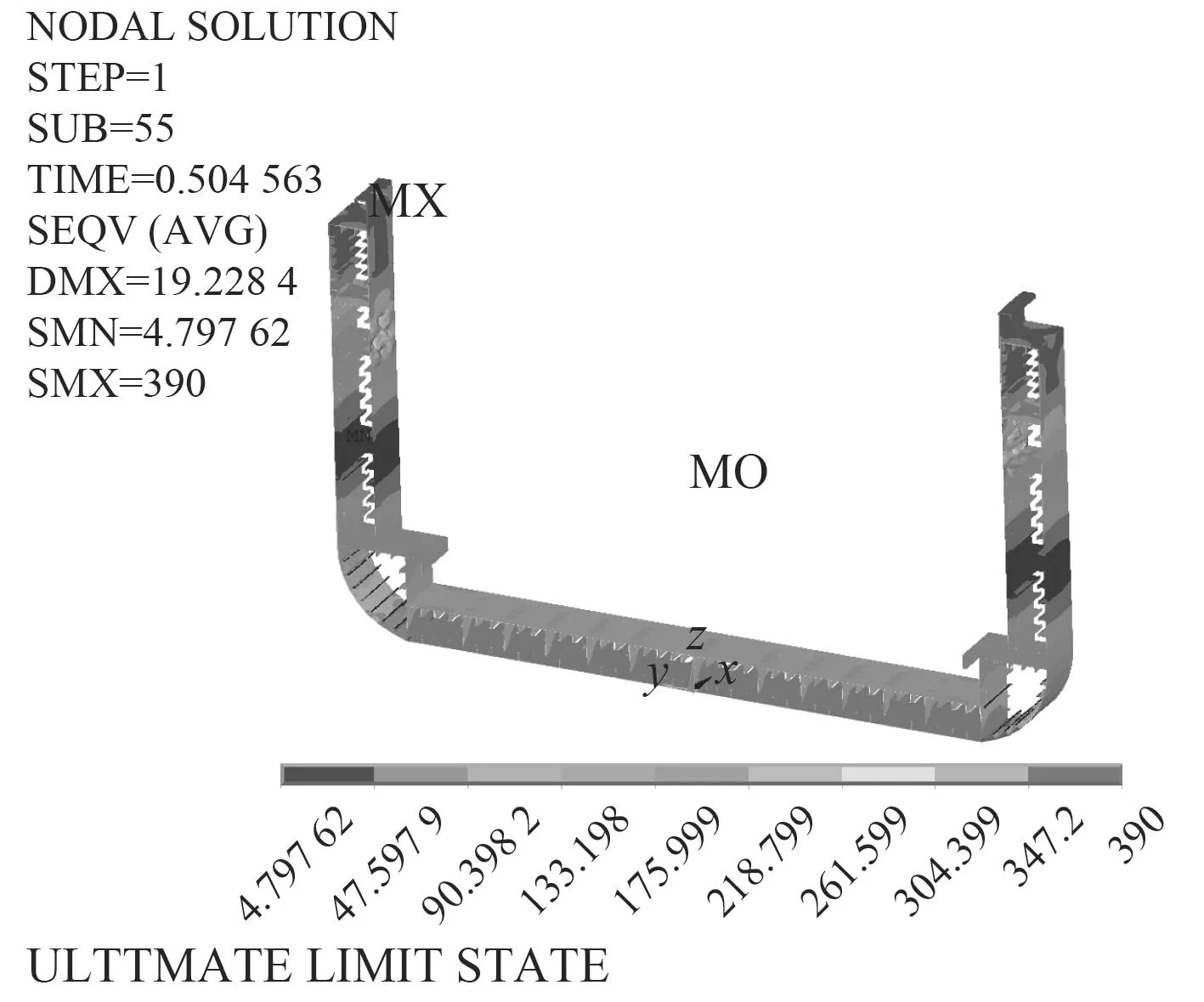
图13 中垂极限弯矩下的应力云图Fig.13 Stress under the sagging ultimate moment

图14 中拱极限弯矩下的应力云图Fig.14 Stress under the hogging ultimate moment

图15 水平极限弯矩下的应力云图Fig.15 Stress under the horizontal ultimate moment

5 结果对比分析

本文采用基于逐步破坏法的MARS2000软件和基于非线性有限元法的Ansys软件，针对10 000箱集装箱船典型货舱结构进行极限承载能力计算，结果对比见表2。

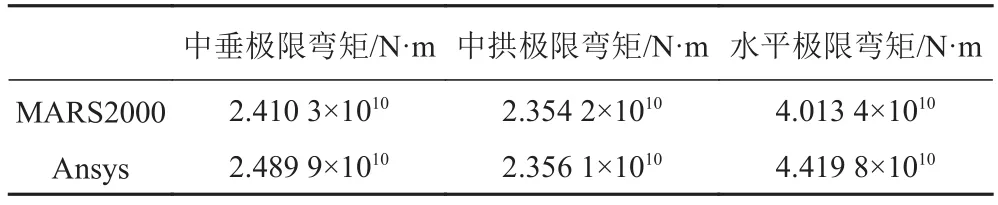
表2 两种方法计算极限强度结果对比Tab.2 Comparison of the ultimate strength results with two methods

从表中可以看出，MARS2000软件计算的中垂极限弯矩和中拱极限弯矩比Ansys软件的结果偏小但相当接近，说明MARS2000软件在标准模式下离散加筋板单元时应用的应力-应变关系，即6种失效模式定义比较准确，而Ansys软件能够更加清晰地识别出加筋板格发生具体的失效模式及位置。水平中和轴的重新分布也充分验证了两者计算结果的准确性。

另外，MARS2000软件可以设定水平弯曲与垂向弯曲的曲率比值或者水平弯矩与垂向弯矩的比值，从而可以考虑水平弯曲和垂向弯曲联合作用下的极限强度。当令垂向弯矩为0时，即可获得水平极限弯矩，但是MARS2000软件计算的水平极限弯矩要比Ansys软件计算的结果小约10%，可能是在水平弯曲时低估了某些构件的承载能力。

6 结 语

本文针对1艘10 000箱集装箱船典型货舱结构的中横剖面，分别采用逐步破坏法的MARS2000软件和非线性有限元Ansys软件，计算垂向和水平极限承载能力。

从大型集装箱船中横剖面典型结构的极限承载能力计算结果对比中主要得到如下结论：

1）逐步破坏法基于平面假设，在将船体结构中横剖面纵向构件划分加筋板单元的基础上，可以分别计算若干个船体剖面的垂向极限强度，比较直观和便捷，建模和计算的耗时少，按照说明文件或提示较易实施，适用于初步设计阶段快速获取船体梁的中拱和中垂极限强度。但MARS2000还不开放定位每个载荷步中结构真正的失效模式，当然这个可以根据Smith方法进行编程获得。逐步破坏法在评估中垂极限弯矩、中拱极限弯矩和水平极限弯矩时的结果均比有限元的方法小，对于工程设计而言偏于安全。

2）非线性有限元方法需要建立完整的舱段结构，建模的难度和计算分析的准确性对工程师的要求较高，该方法不仅能够准确计算垂向极限弯矩，还能评估水平极限弯矩，并且可以观察在进入后屈曲阶段船体剖面结构的失效模式及其发生的位置。因此，在结构设计阶段和送审设计阶段，建议采用非线性有限元法对船体货舱结构进行直接计算，针对最容易失效的板材或骨材，进行局部补强或加厚尺寸，切实做到真正提高集装箱船货舱结构极限承载能力。