MODIS遥感产品在三江源地区草产量估测中的应用
2018-12-20曹西凤孙林赵子飞韩晓峰颜明捷
曹西凤, 孙林, 赵子飞, 韩晓峰, 颜明捷
(1.山东科技大学测绘科学与工程学院,青岛 266590;2.山东科技大学数学与系统科学学院,青岛 266590;3.山东地质测绘院,济南 250000)
0 引言
三江源地区地处干旱半干旱区,其草地面积占我国草地总面积的30%左右;草场的生长不仅决定着畜牧业的发展,也深刻影响着三江源地区生态系统的平衡;合理精确地预测草场牧草产量可为引导畜牧业生产、合理利用草地资源及维持生态平衡提供保证[1]。
传统的牧草估产以站点实测居多,采用的方法有“双重采样法”及“割重法”等,基于站点实测可以得到较高的草场估测精度,但时间周期长,且人力物力利用率低,不适合于像三江源地区这样面积较大、地表结构较复杂区域的牧草估产[2]。随着遥感技术的发展,草产量估算开启了新时代,研究人员发展了多种草场草产量估测模型。目前采用的主要方法有基于植被特征参量的遥感统计方法和基于气象因子的草产量预测方法2类。全球气象卫星为草产量的估测提供了丰富的资料,使草产量模型从一元模型发展到了多元模型,从一阶多项式过渡到了高阶多项式,模型精确度逐渐提高[3-5]。但是,已有的草产量估算的研究大多在气候温和、降水适中且草产量监测站点较多的地区进行,牧草产量的估测精度较高,结果验证也较为简便。而在我国的西北部地区,如三江源地区,因位于高寒地带,面积广阔、人迹罕至、同一时间内大范围数据获取困难、监测站点较少、实测数据缺乏且相关性较大,使得模型建立困难,拟合精度不高。尽管部分研究建立了某些气象因子与草产量之间的联系,对草产量精度的提高起到了一定推动作用[6-7],但仍缺乏遥感数据与气象数据的综合使用,未从对草产量变化产生影响的直接因素与间接因素入手,更加合理地解释草产量的变化趋势。此外,随着国家对保护生态环境工作的重视,已开展的省级、县级草产量统计数据不断增多,而应用较少。
植被指数通过少量波段组合的信息,反映植物生长状况、植被覆盖、生物量及作物产量,在国内外草产量的估测和预报中应用较广且精度较高。常用的植被指数有比值植被指数(ratio vegetation index, RVI)、归一化差值植被指数(normalized difference vegetation index, NDVI)、增强型植被指数(enhanced vegetation index, EVI)、土壤调节植被指数(soil-adjusted vegetation index, SAVI)、修正土壤调整植被指数(modified soil-adjusted vegetation index, MSAVI)等[8-13]。本文综合考虑了多种植被指数及气候状况对草产量的影响,结合多元线性回归及偏最小二乘回归(partial least squares regression, PLS)理论,提出了基于多种MODIS产品的牧草产量预测方法,用于三江源地区草地草产量的评估,结合三江源地区草地生态监测站点实测的草产量数据,进行草产量预测,并验证了其预测精度。
1 研究区概况及数据源
1.1 研究区概况
三江源地区(E89°45′~102°23′,N31°39′~36°12′)位于我国青海省的南部,因地处长江、黄河、澜沧江的源头而得名(图1)。行政区域包含4个藏族自治州(玉树、果洛、海南、黄南)的16个县及格尔木市唐古拉乡。该区河网稠密,河流众多。区内以青藏高原气候系统为主,冷热两季交替,干湿两季分明,降水空间分布不均匀。地形以山地为主,平均海拔3 500~4 800 m,面积广阔,西北部有少量冰川分布。草场主要分布于该区东南部,面积约占全区总面积的70%左右,分布不均匀,自东向西草产量呈递减趋势。草场类型众多,有植被覆盖度较低的高原宽谷荒漠草场、中等植被覆盖度的高山草甸草场、高植被覆盖度的山谷稀疏森林草场和湖盆滩地草甸草场等。
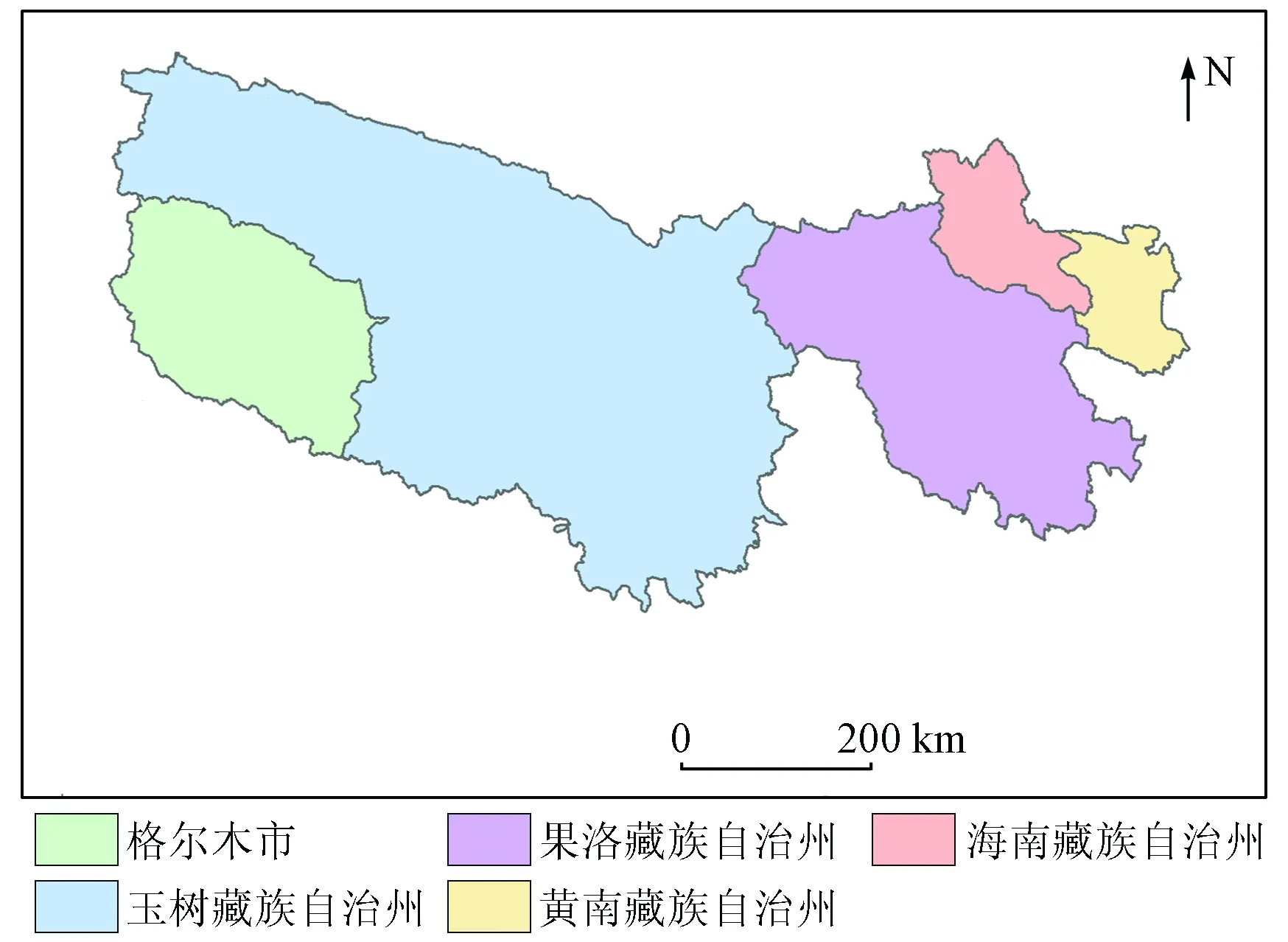
图1 研究区地理位置示意图
1.2 数据源介绍
遥感数据源为MODIS中等空间分辨率成像光谱仪数据。MODIS通过其0.4~14 μm的36个光谱通道实现全光谱范围覆盖,空间分辨率包含3个等级:250 m,500 m和1 000 m,每1~2 d即可实现一次全球覆盖。本文选取的MODIS产品数据包含:MCD12Q1——土地覆盖类型(Land_Cover_Type1, LC)、MOD11A2——地表温度(land surface temperature, LST)&发射率(Emissivity)、MOD13A2——NDVI&EVI、MOD15A2——叶面积指数(leaf area index, LAI)&光合有效辐射吸收比率(fraction of absorbed photosynthetically active radiation, FPAR)、MOD17A2——总初级生产力(gross primary productivity, GPP)共140景,上述MODIS陆地产品数据的详细信息如表1所示。产品数据的存储格式均为HDF,参考椭球为WGS 1984椭球,投影为中国地区Albers投影。
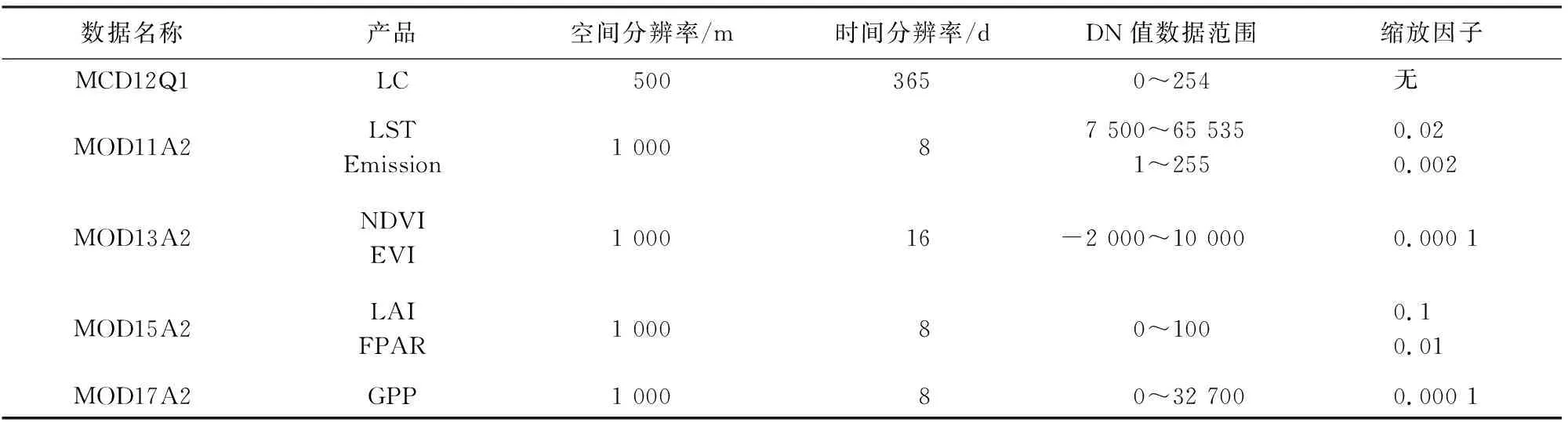
表1 MODIS陆地产品数据信息
2 MODIS数据处理
选取研究区2009年4月中旬—10月初期间11期140景数据,通过MODIS 投影工具(MODIS reprojection tool,MRT)进行了数据批量预处理,并基于ArcGIS软件建模,对数据进行了统计分析。
对各草地监测站区域内MODIS产品数据进行统计分析,得到NDVI,EVI,LAI,FPAR和GPP因子在各生长期的均值及整个生长期内的LST均值。预处理结果包含研究区2009年第113—273天共11期草地生长期内的6种MODIS产品监测数据,前5种因子分别如图2—6所示。

(a) 第113日 (b) 第129日 (c) 第145日

(d) 第161日 (e) 第177日 (f) 第193日

(g) 第209日 (h) 第225日 (i) 第241日

(j) 第257日 (k) 第273日

(a) 第113日 (b) 第129日 (c) 第145日

(d) 第161日 (e) 第177日 (f) 第193日

(g) 第209日 (h) 第225日 (i) 第241日

(j) 第257日 (k) 第273日

(d) 第161日 (e) 第177日 (f) 第193日

(g) 第209日 (h) 第225日 (i) 第241日

(j) 第257日 (k) 第273日

(a) 第113日 (b) 第129日 (c) 第145日

(g) 第209日 (h) 第225日 (i) 第241日

(j) 第257日 (k) 第273日

(a) 第113日 (b) 第129日 (c) 第145日

(d) 第161日 (e) 第177日 (f) 第193日

(j) 第257日 (k) 第273日
由图2可知,NDVI越高,草越旺盛,生长状况越好,反之,植被越稀疏,生长状况越弱。时间上,由初夏到秋末NDVI总体呈先增后减趋势,研究区中部尤为明显,第145—161天NDVI大幅度增加;空间上,东部处于匀速增加阶段,西部较稳定。
由图3可知,在时间上,由初夏到秋末EVI总体呈现先增后减的趋势;空间上,研究区东南部EVI值高于西北部,且在植被生长过程中西北部EVI变化缓慢。
由图4可知,LAI越大,单位面积内植被叶片数量越多。时间上,由初夏到秋末LAI总体呈上升趋势;空间上,东西差异较大,在三江源地区西部区域相对稳定,处于较低水平,中部和东部地区都有明显的上升趋势。
由图5可知,FPAR越大,草对光能的利用率越高;反之,草对光能的利用率越小;光能利用率的高低间接影响着草产量的分布。在时间上,由初夏到秋末FPAR总体呈先增后减趋势,在研究区中部区域尤为突出;空间上,西部光能利用率偏低。随时间推移,中南部地区逐渐向光能利用率高的水平过渡,增长趋势明显。
由图6可知,GPP越大,植被光合作用固定有机物含量越高;反之,植被光合作用固定有机物含量越低。在时间上,由初夏到秋末GPP总体呈先增后减趋势;空间上,西部GPP偏低,东部光能利用率高,变化不明显。
将各个遥感监测因子在每个生长期的均值导出统计数据为自变量X,其中包含11个时期的上述5种MODIS产品及整个生长期内的LST均值共56个解释因子。草地监测站2009年6—8月实测草产量为因变量Y,共3个被解释因子。
3 草产量模拟方法
3.1 多元线性回归
多元线性回归分析是用于模拟一个被解释变量与多个解释变量之间的关系模型,主要根据样本的观测值估计回归模型中各个解释变量的系数,其中最常用的方法为最小二乘估计。
多元线性回归的基本形式为
Yi=a1X1i+a2X2i+a3X3i+…+akXki+bi,
(1)
式中:Yi为第i个样本的被解释变量;a1,a2,...,ak为k个回归系数;X1i,X2i,…,Xki为k个解释变量;bi为回归常数。
对于每个样本构建式(1)所示方程,即
(2)
再根据最小二乘法,即误差平方和最小原则,求得回归方程各个系数,得到产量预测模型。
3.2 PLS
与多元线性回归模型不同的是,PLS考虑了变量之间的相关性,通过提取变量的主成分削弱变量之间的相互影响,使模拟结果更可靠。
PLS与主成分分析类似,都是通过自变量与权阵的加权和得到几个正交分量进行降维,在具体的提取及系数确定过程中有所差别。该方法首先对原始解释因子进行分析,得到一阶成分。一阶成分拥有对所选解释因子的最大解释能力;将所得第一个成分对解释因子拟合后的残差作为新的解释因子,得到二阶成分。以相同的方式循环操作,得到更高阶成分,用于对草产量的拟合。通过成分的提取可消除解释因子之间的相关性,减弱部分解释因子噪声的干扰,使拟合精度有所提高。PLS主要计算步骤如下:
1)将站点实测草产量数据定义为一个n维列变量Yn×1,提取的自变量定义为矩阵Xn×m,将Xn×m和Yn×1进行中心化处理得到新的变量X0和Y0,即
Y=(y1,y2,…,yn)T
(3)
(4)
2)提取X0第一个主成分分量α1,即
α1=X0a1
(5)
式中a1为单位特征向量,可由拉格朗日定理求得。
3)建立X0与Y0对α1的回归,即
(6)
式中:P1和Q1分别为X0和Y0的回归系数向量;X1和Y1为回归一次后的残差矩阵。
4)循环输出结果。用X1和Y1代替X0和Y0提取二阶成分α2,直至提取r个成分。其中,阶数r通过“交叉有效性”来确定,最终回归方程为
(7)

3.3 精度评价原理
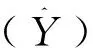
为定量化描述预测结果的好坏,选取决定系数(R2)、期望误差(expect error,EE)和均方根误差(root mean square error,RMSE)进行精度验证,表达式分别为
(8)
EE=±0.2YieldMeasured
(9)
(10)
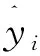
4 模型建立与分析
4.1 多元线性回归模型
使用多元线性回归方法进行草产量模拟。针对不同月份影响因素的差异性,分别与选取当月实测值相关性较大的5个参量作为解释变量,建立解释变量与实测值的多元线性回归模型。具体模型如表2所示,3个月的草产量实际值分别表示为Y1,Y2,Y3;解释变量表示为Xab的形式,以XFPAR129为例,表示第129天的FPAR产品作为解释变量之一,其中FPAR为MODIS的产品名,129为数据获取日期(年积日)。3个不同时间段拟合结果不同,在不同时间段,对草产量影响占主导地位的因素也不同。

表2 多元线性回归模型
4.2 PLS模型
4.2.1 累计解释能力与交叉有效性
为去除各个解释因子之间的相关性,对解释因子进行了成分提取。对于提取的成分要对解释因子具有最大解释能力,即能概括性地表达解释因子中所包含的信息。以提取的成分为跳板建立草产量解释因子与实测草产量之间的关系。
在草产量估计中,从解释因子中提取多个主成分,分析这些成分与草产量的关系。图7显示前8个主成分分量的累计解释能力,分别为从Comp[1]~Comp[8],R2Y为选取主成分与草产量的解释能力,R2Y的值越趋近于1,拟合数据越准确;Q2为成分与模型的交叉有效性,Q2越接近于1,预测效果越好。
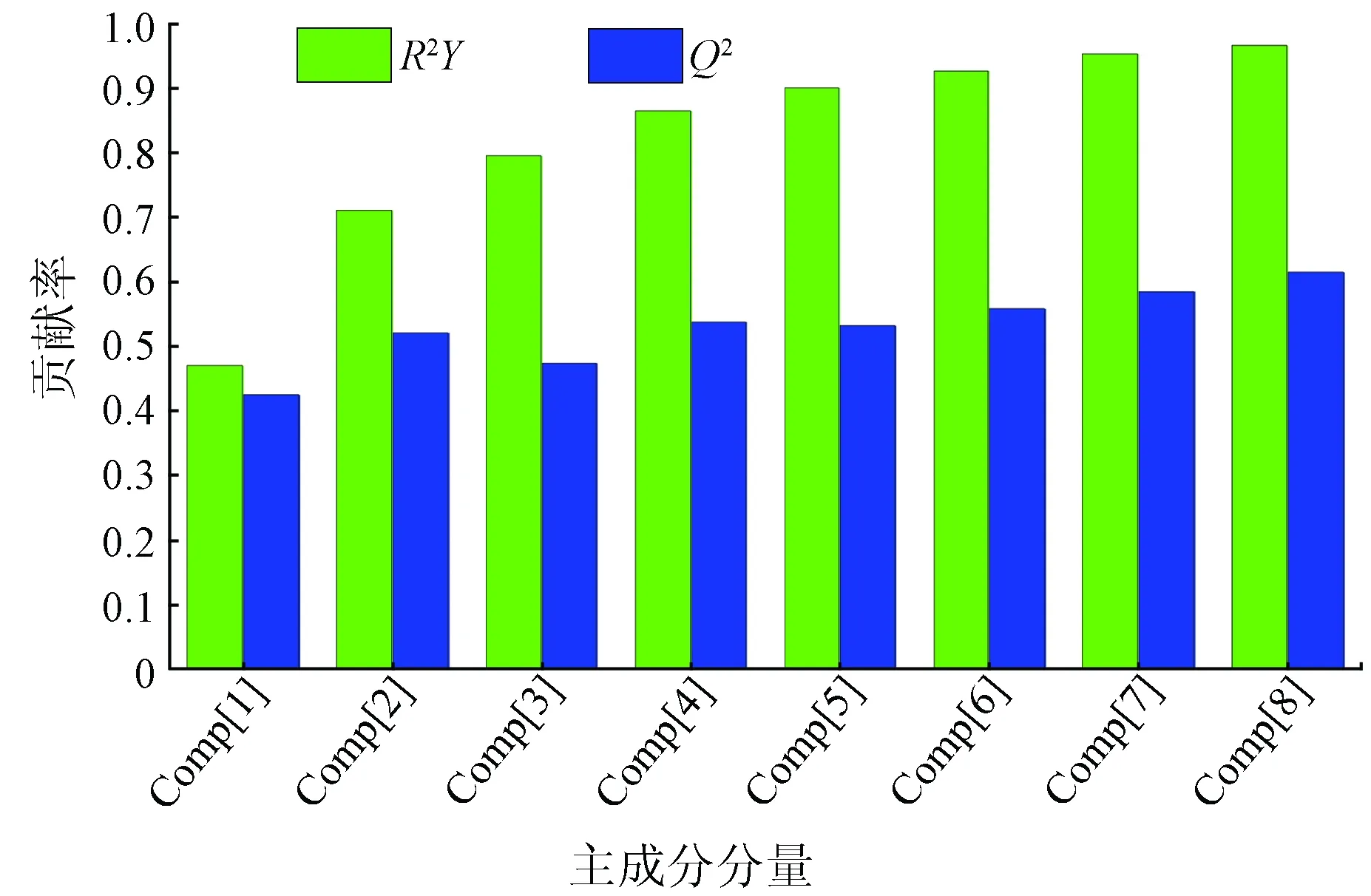
图7 主成分分量累计解释能力
用于模拟分析的成分个数增多,累计解释能力增加,模型交叉有效性先呈上升的趋势,之后成分数继续增加,拟合精度不再发生较大变化。如果用于模型拟合的成分数逐渐增多时,就意味着综合成分对模型的解释性越强,所包含解释因子的信息量也就越丰富,模型拟合精度相应就会得到提升;但当成分数达到一定程度,包含信息量达到饱和,成分数继续增加,信息量的变化不再像之前那样明显。预测精度随成分个数的增加,拟合精度迅速增加,之后逐渐趋于平衡。在主成分分量对模型的累计解释能力>80%且交叉有效性>60%的前提下,选取前5个主成分分量进行最终草产量预测。
4.2.2X与Y的相关关系
将56个解释因子作为解释变量,2009年6—8月草产量作为被解释变量。选用解释变量与被解释变量的一阶主成分为代表,验证草产量与解释因子之间的相关性。一阶主成分相比于其他数据能较完整地概括数据的信息,对复杂的数据进行降维。采用t[1]/u[1]平面图可以判断两者的相关关系(图8),其中横坐标为解释因子的一阶成分t[1],纵坐标为草产量一阶主成分u[1],从总体趋势中可以看出模型选取的6种MODIS产品与草产量之间存在较好的相关性,t[1]/u[1]平面图表明用PLS实现草产量估算是可行的。

图8 t[1]/u[1]平面图
4.2.3X对Y的解释作用
草产量由多种解释因子共同决定,地位较高的因子起决定性作用。用变量投影重要性指标(variable importance for the projection, VIP)作为自变量对因变量的影响地位的测度,其中VIP平方和等于模型中因子的项数,因此平均VIP等于1。VIP越高变量贡献值越高,对预测值的解释能力越强。当VIP<1时,该变量解释能力较弱(图9)。
解释因子按重要性由高到低、从左到右进行排序。其中对草产量影响最显著的指标是2009年第129天的LAI及2009年第129天的FPAR数据。从总体趋势来看,植物生长期内GPP对草产量的影响较大,随时间变化波动小,NDVI,EVI和LAI对草产量的影响随时间变化波动大。
4.2.4t1/t2平面图与T2椭圆
使用解释因子前2个主成分分量t1和t2分别作为横纵坐标绘制其相关系数散点图,其作用与主成分分析中的主平面图类似,图10中样本点越接近表明2个样本在原自变量空间的高维性质越相近。图10中的椭圆为T2椭圆,为95%置信区间,椭圆中的采样点分布越集中,表示原始样本数据分布越均匀,误差越小;分布越离散,则误差越大。若有样本点偏离范围,处于椭圆外,可判定为异常值。由图10可看出所选样本的数据在T2椭圆中分布较为均匀,误差较小,不存在异常值,因此所选因子构建模型的估算结果与实测数据之间不会产生太大偏差,无需改动。

图10 t[1]/t[2]平面图
4.2.5 数据重构质量
通过监测点在X(Y)上的标准化模型距离检查每个生态监测站在X(Y)上的重构质量,可以对预测质量进行评估(图11—12),2幅图的横坐标均为各个草地生态监测站点,其中,图11纵坐标为监测点在Y上的模型距离(DModY);图12纵坐标为监测点在X上的模型距离(DModX)。
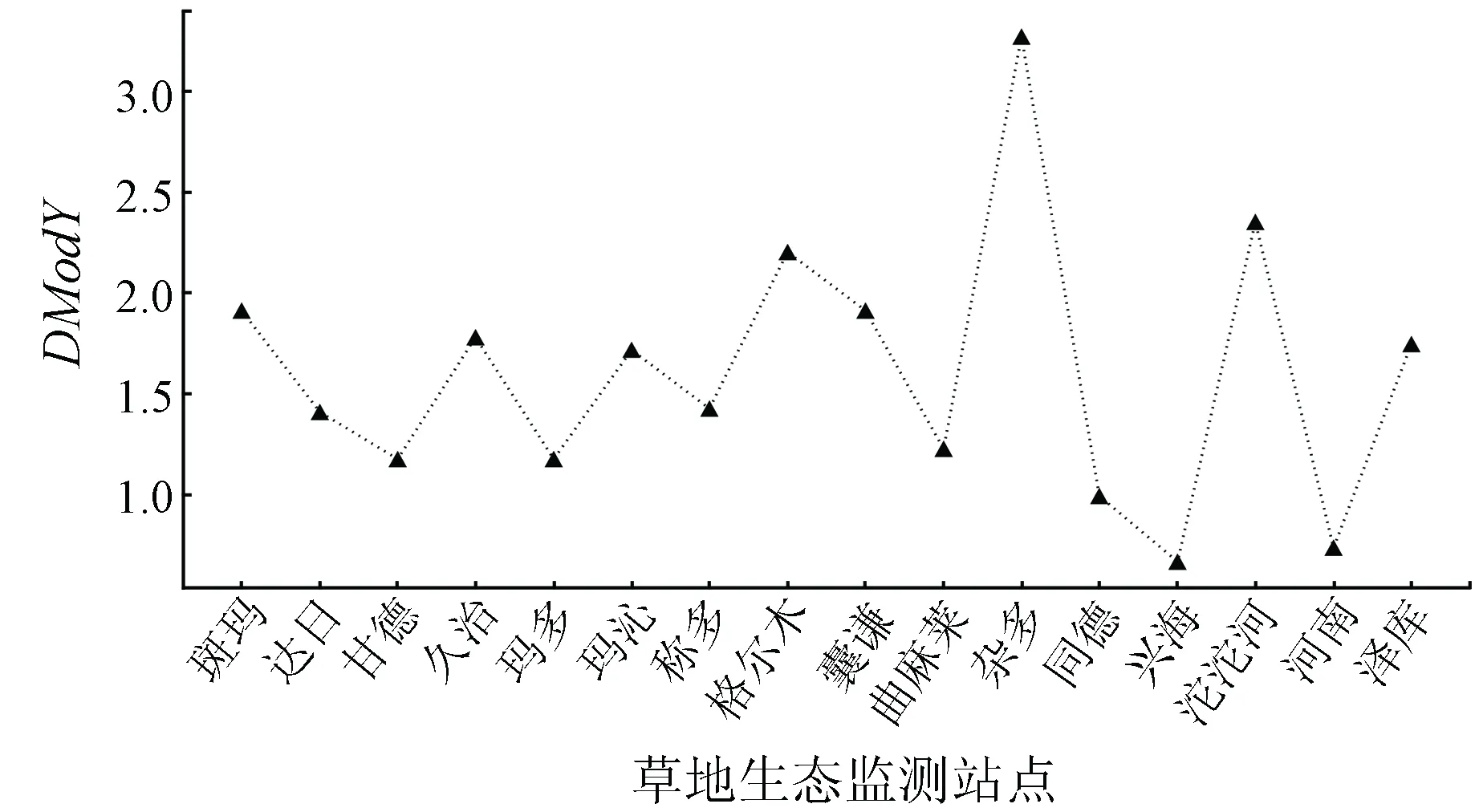
图11 监测点在Y上的标准化模型距离
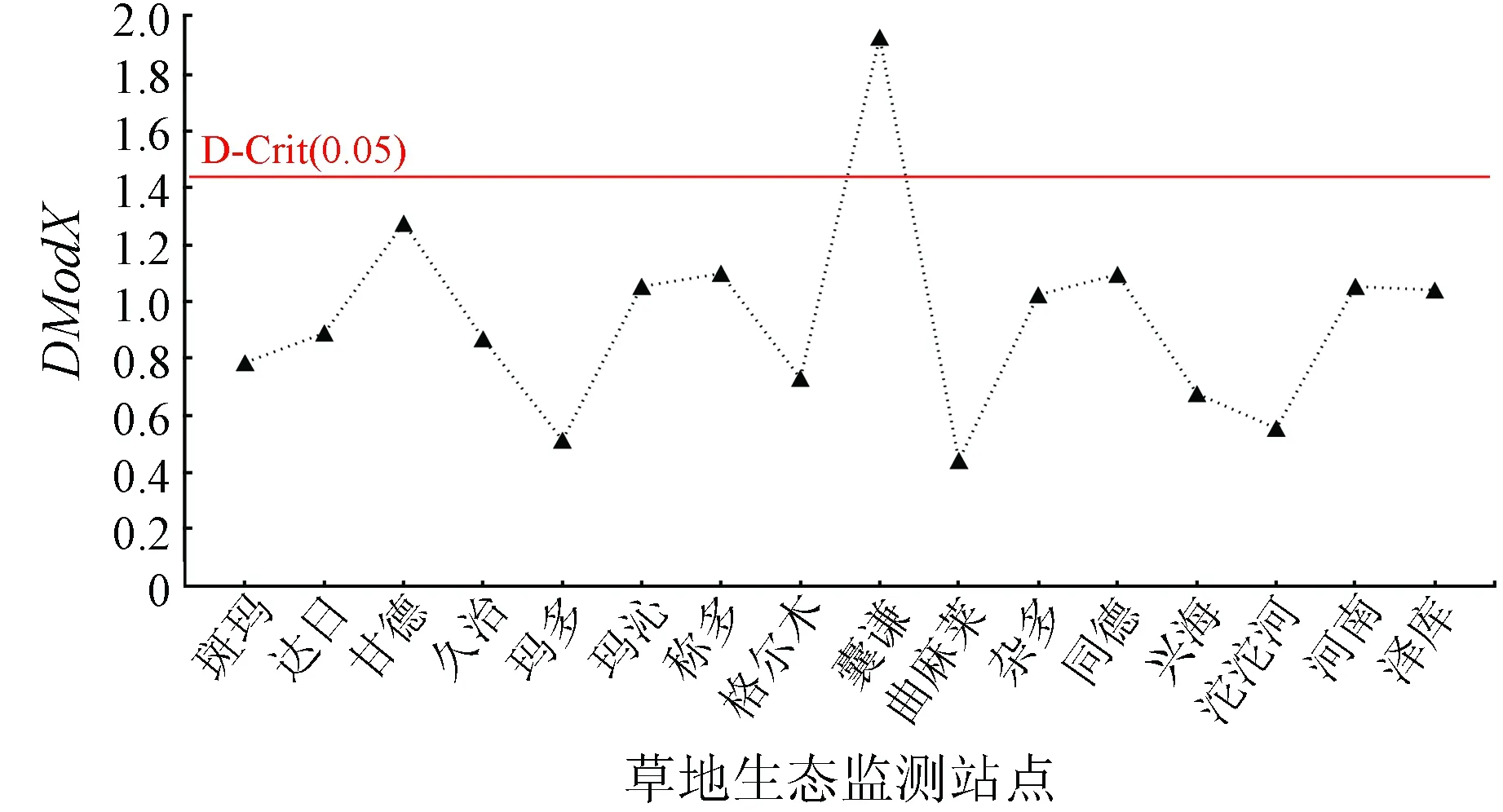
图12 监测点在X上的标准化模型距离
从图11—12可以看出,杂多县在Y上的DModY距离较大,囊谦县在X上的DModX距离也处于游离状态,表明两者重构质量不理想。
4.2.6 预测结果
基于公式(7)得模型常数项如表3所示。

表3 模型常数项
为了更直观地显示各期产品对草产量的预测建模的含义解释,绘制了2009年6月草产量模型的系数(图13),2009年7月和8月份类似。
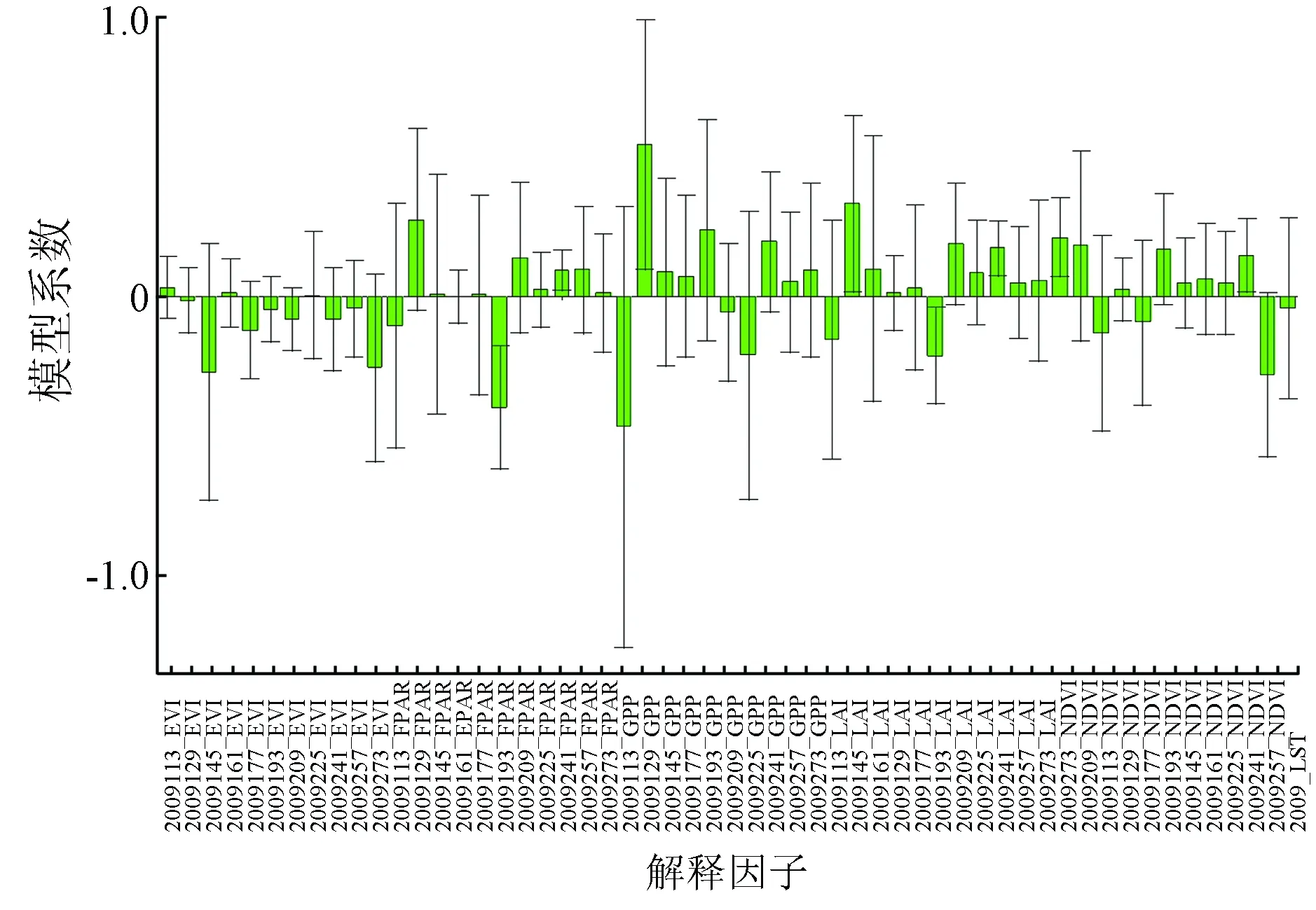
图13 2009年6月草产量估算模型系数
从图13可以看出,建立的草产量预测模型中各个解释因子的系数,零值以下为负,以上为正,当系数为正时,说明该解释因子与草产量成正相关;当系数为负时,说明该解释因子与草产量成负相关,相关系数越高,说明该因子越重要。总体结果与VIP重要性指标分析基本吻合。
4.2.7 精度验证
为检验草产量估测模型的鲁棒性,基于2009年数据建立的草产量预测模型,使用2011年的数据进行精度验证。以2011年预测草产量为X轴、实测草产量为Y轴绘制实测草产量与预测草产量之间散点图(图14),可以直观对比预测模型的精度和拟合稳定性。图14中分别为2011年6—8月多元线性回归分析结果和PLS分析结果,黑色虚线表示草产量EE,处于虚线以上的点表示草产量预测值高于期望值,虚线以下的点表示预测值低于期望值,虚线之间的点表示满足期望误差。在草产量预测值/实测值散点图中,利用PLS构建草产量预测模型体现了很好的稳定性,总体上能反应两者的线性关系,与多元线性回归相比,PLS具有较高的R2(0.829~0.878)和较低的RMSE(42.457~93.674 kg·hm-2)。
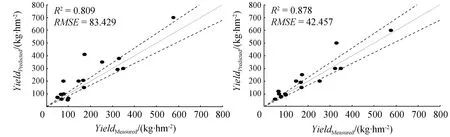
(a) 6月多元线性回归结果 (b) 6月PLS结果

(c) 7月多元线性回归结果 (d) 7月PLS结果

(e) 8月多元线性回归结果 (f) 8月PLS结果
5 结论
本研究以MODIS产品数据(NDVI,EVI,FPAR,LAI,GPP,LST)为数据源,基于多元线性回归法与偏最小二乘回归(PLS)分别建立了2009年6—8月的三江源地区草产量预测模型,并用2011年相应数据进行了验证,结果表明:
1)基于PLS的草产量预测模型对该地区的适用性高于多元线性回归,整体呈现出较好的相关性。
2)基于PLS,利用MODIS产品数据可以有效地实现三江源地区草产量估算。解决了三江源地区因子间相关性较大、环境恶劣、样本少且采样困难的问题。
3)在研究所选取的MODIS 产品中,草产量与GPP及LAI的相关性较大。
4)草产量预测结果以6月份效果最佳,其中R2为0.878,均方根误差为42.457 kg/hm2。
志谢:感谢国家地球系统科学数据共享平台提供的数据资源。
