大气加权平均温度本地化模型研究
2018-12-20薛骐
薛 骐
(中国铁路设计集团有限公司,天津 300000)
美国Askne等[1]在1987年提出了利用GPS探测大气的概念,并且成功推导出了大气湿延迟和水汽PWV之间的相互转换关系。PWV和天顶湿延迟之间的转换系数Π与Tm值的大小有直接关系。Tm定义为局部地区的气柱中考虑水汽压权重垂直积分的平均温度[2]。2001年,Fores[3]做了对比实验,比较了映射函数值与真实值之间的差值。2006年,Boehm[4]等推导了全球映射函数GMF。但是气压、温度是随着时间和空间变化的,故Tm也具有时空变化性。此外,由于水汽的空间分布不均,时间变化较复杂,无法得到精确积分值。所以,实时计算对流层加权平均温度的难度较大,这也是地基GPS水汽反演中控制误差的关键问题。
Tm值受多方面影响,包含地表温度、水汽压垂直分布情况和对流层分层大气温度等。采用固定Tm值,会对结果产生较大误差。以中国香港地区举例来说,假设湿延迟ZWD=500 mm,若要保证大气可降水量转换精度优于1 mm,Tm的精度就需优于3.4 K[5]。谷晓平等[6]利用四川地区某探空站5年的探空资料,以大气加权平均温度作为因变量,以露点温度、温度、水汽压和地表气压当成自变量,使用回归分析的方法建立计算模型,证明本地化的订正公式比Bevis公式误差更小、精度更高。所以Π的误差直接受Tm模型精度的影响,进而影响水汽反演的结果。因此,Tm的本地化修正很有必要。
1 大气加权平均温度Tm原理
1.1 大气加权平均温度Tm
对流层湿延迟占总延迟的10%~20%[7],由于其变化速度快,难以用固定模型进行描述。天顶湿延迟(ZWD)等于天顶总延迟(ZTD)减去天顶干延迟(ZHD),将天顶湿延迟(ZWD)乘以转换系数Π,得大气可降水量PWV

(1)
转换系数Π计算公式[8]为
(2)
公式(2)中,ρw=水汽密度,Rv=水汽气体常数,Mv,Md分别是水汽、干空气分子摩尔质量,k1、k2、k3是大气折射系数,k1=77.689 0 K·hPa-1,k2=71.295 2 K·hPa-1,k3=375 463 K2·hPa-1。
Tm是大气加权平均温度[9]
(3)
公式(3)中,H是测站高度/km,e是水汽压,T是绝对温度。Td是露点温度,es是饱和水汽压,es0是0 ℃时饱和水汽压(6.11 hPa)。水面上a0=7.5,b0=273.3;冰面上a0=9.5,b0=265.7[10]。
其中,Π是无量纲数值,与Tm有关。
1.2 加权平均温度的计算方法
(1)取常数值法[11]
水汽转化系数Π在1/6.5左右,所以Π可以取值1/6.5,计算得Tm=269.7。这种方式精度较低,只适合低精度的可降水量估计。
(2)近似积分法[12]
为附加条件的积分过程。三个条件为:满足水汽动力学方程、对流层大气为理想气体、气温随高度的递减率为常数。
e=es(p/ps)λ
(4)
公式(4)中,es是地面水汽压,ps是地面总气压,e为任意高度上的水汽压值,p为任意高度上的总气压值,递减参数λ为常数,积分结果近似表达为
(5)
公式(5)中,g是重力加速度,R是气体常数,Ts是地面气温。
(3)利用数值预报值计算
利用数值预报模式可以对Tm进行解算,但精度较差。
(4)Bevis回归经验模型[13]
该模型采用美国13个探空站获取的两年观测资料进行解算,在全球范围都能进行较好地模拟,代表性较强。考虑到本地化差异,获得的结果不能保证最优。所以需本地化改正,Bevis方法公式为
Tm=70.2+0.72·Ts
(6)
(5)探空资料数值积分法[14]
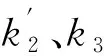
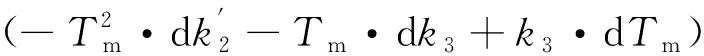
(7)
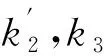

(8)
根据合适的Tm可以进一步得到转换参数的最大误差ΔF。σF是Tm的增大函数,通过最大的Tm就可以得到σF。中国香港地区最大的Tm可以达到300 K,将其代入公式(8),得σF和σT的关系式
(9)
根据表1中ΔF与σT的对应关系,可以假设WZD=500 mm,则由PWV与Ts转换公式引起的误差可以求得。对流层加权平均温度的精度取决于转换参数的精度,在对流层加权平均温度的精度优于3.4 K情况下,转换精度能够控制在1 mm以内。
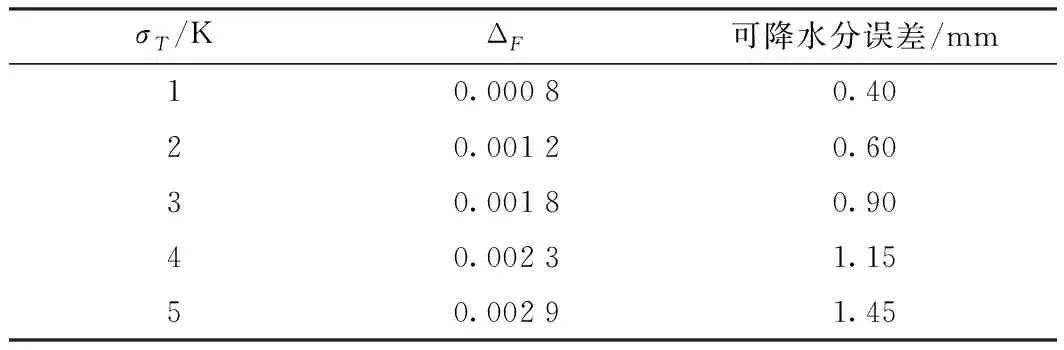
表1 ΔF 与σT 对照
2 加权平均温度Tm本地化
2.1 数据的选取
Tm具有随时间、地域变化的特性。本文研究对象是中国香港地区2016年10月份加权平均温度情况,所以使用中国香港地区Kings Park探空站2014~2016三年10月份的探空数据,进行Tm数据的本地化改进。表2中第一列PRES为气压,HGHT为距离地面的高度,TEMP为温度,数值积分只用以上三列数据进行计算。

表2 探空数据文件[16]
大气水汽主要分布在12 km以内,而无线电探空气球可提供20 km以内高空的湿度、温度、气压的测量结果,这里用数值积分方法来逼近Tm。
(10)
公式(10)中,h2、h1为相邻两次观测的高度值;e和T是h2、h1之间的平均水汽压以及绝对温度。根据文献 [17],使用该方法造成的误差综合影响要小于1 K。因此,可使用回归分析方法确定Tm和地面温度的相关关系。
2.2 本地化改进及精度检验
计算得到均方差为1.81,通过回归分析确定最佳模型为
Tm=117.055+0.570·Ts+273.15
(11)
Bevis公式[18]加权平均温度模型为
Tm=70.2+0.72·Ts+273.15
(12)
这里一并给出由刘焱雄[19]根据1996年9月~1997年10月探空数据计算的模型
Tm=272.4+0.556·Ts
(13)
为验证各模型的精度,根据2014~2016年10月份探空资料,加权平均温度散点图以及三种模型的比较如图1所示。
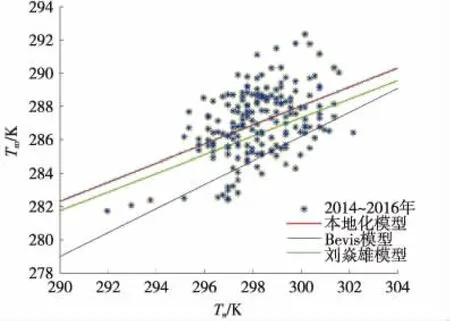
图1 加权平均温度拟合模型
因为加权平均温度变化复杂,受到气压、风速、湿度等很多因素的影响,从图1可以看出,该模型拟合程度较好,但与本地化Tm拟合模型相比仍有1 K左右误差。对比本地化模型和Bevis模型发现,Bevis模型的效果明显更差,下面从两个模型的具体误差进行说明(如图2)。
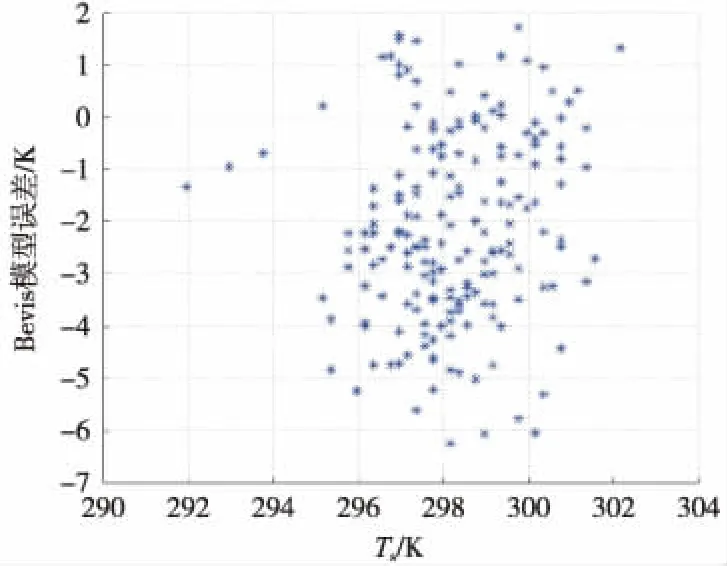
图2 Bevis模型误差分布
由图2的误差分布情况可以看出,Bevis模型有接近1/3计算结果超过了3.4 K的误差阈值,还有部分数据达到了7 K的误差,对水汽解算的结果会产生1~2 mm的误差。下面给出本地化模型误差(如图3)。
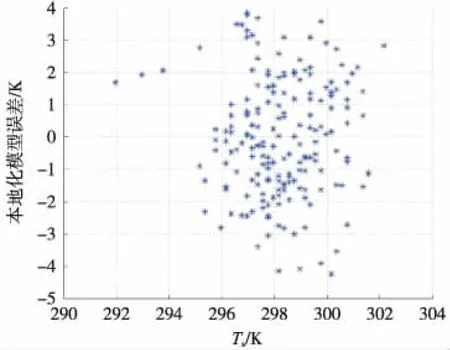
图3 本地化模型误差分布,
对误差分布情况进行分析,本地化加权平均温度模型总体情况良好,虽然有8组结果超出3.4 K误差阈值,但是从三年的数据来看,这种现象是正常的。可以看出,该模型的计算精度能够满足地基GPS水汽反演中转换精度的要求。
3 结论
(1)加权平均温度受气压、风速、湿度等多因素影响,具有时域性和区域性,所以需要本地化改进。
(2)转换参数的精度受对流层加权平均温度的精度影响,在对流层加权平均温度的精度优于3.4 K情况下,转换精度能够控制在1 mm以内。
(3)Bevis模型有接近1/3计算结果超过3.4 K误差阈值,还有部分数据达到了7 K的误差,对水汽解算的结果会产生1~2 mm的误差。
(4)本地化加权平均温度模型在结果上较Bevis模型好,该模型的计算精度能够满足地基GPS水汽反演中转换精度的要求。
