基于I-GARCH的不确定时间序列概率分布推算
2018-12-20汤其婕
汤其婕,王 玙
(南京航空航天大学 计算机科学与技术学院,江苏 南京 211106)
0 引 言
时间序列(time series)是一种典型的高维数据类型,其在传感器网络、位置定位服务(location based service,LBS)、环境监测、医疗检测、物联网等众多领域应用广泛[1-2]。但是,受数据采集设备的缺陷或者人为因素的影响,采集得到的数据在一定范围内存在偏差。将这类型的数据定义为不确定时间序列(uncertain time series)。而针对不确定时间序列的有效存储,到目前为止仍没有良好的解决方案。
一种处理不确定数据最有效的方案是概率方法。近年来许多专家和学者提出了一系列的方法用于解决不确定数据的管理和查询问题[3-9]。这些方法有一个共同特征,即假定用于进行查询的概率数据是已知的,可以直接获取到。但是,现实情况并非如此。不确定时间序列的概率是由推导出这些概率的概率分布函数决定的,这些概率分布函数以时间为坐标不断发生变化。简而言之,不确定时间序列的概率值随时间不断变化,无法得到其固定值,因此无法使用已有的概率数据库生成方法直接对其进行存储处理。因此,如何“创造”概率数据仍是未解决的问题,也是文中主要研究的问题。
针对从已知的时间序列推导得到时间序列的概率分布问题,文中主要完成的工作分为两部分。一是依托已有的各种数学模型,结合已有的动态密度指标的概念,提出ARMA-GARCH动态密度指标模型,并对其推算原理进行了详细的分析与介绍;二是针对GARCH模型无法高效处理含错数据的弊端,提出改进的I-GARCH模型。该模型在处理含错数据集时能体现出良好的容错性,更符合一般的不确定时间序列数据的采集规律。最后通过实验进行验证。
1 相关工作
1.1 动态密度指标
时间序列由于依赖时间的变化,通常呈现出很大的不确定性,因此为不确定时间序列数据创建概率数据库的最大挑战之一是处理不断更新的概率分布。如图1所示,该图为一天当中的气温随时间的变化曲线。

图1 气温变化曲线
在临近日出和日落两个时间点,温度的变化十分明显,如A区域所示,但是在夜间的时候,整体的温度变化幅度不大,如B区域所示。两处的概率分布规律明显不一致。如果用相同的概率分布基来表示两处的概率分布,显然不科学。因此,应该随着时间的变化动态地更新用来表示概率分布的概率分布基,使其符合当前数据的变化趋势。由此,引入了动态密度指标的概念。
动态密度指标[10]依托多种数学模型,可以从一条给定的时间序列中动态地推算出随着时间变化的概率分布。然后,由这些动态密度指标推算得到的概率分布就可以用来创建概率数据库,完成数据的存储工作。已有的动态密度指标介绍如下。
1.2 已有动态密度指标
(1)统一阈值指标。
Cheng等[11]提出了一个通用的不确定数据的查询估约框架。它的主要思想是将原始数据进行建模,将建模得到的数据范围作为对应时间点数据的波动范围。同时,该范围也是该时间点所对应的真正值的所在范围。然后在计算出的波动范围中进行查询操作,代替直接在原始值上进行查询。
统一阈值指标(uniform thresholding metric,UT)的思想是上述思想的一种扩展,即通过推导得到对应时间点的一个“预期真实值”,然后以该“预期真实值”代表该时间点的原始真实数值,表示该点的概率分布。“预期真实值”的定义如下。



(1)
其中,(p,q)是非负整数,定义了模型的顺序;φ1,φ2,…,φp是自回归参数;θ1,θ2,…,θq是移动平均参数;φ0是一个常量;t>max(p,q)。
(2)可变阈值指标。
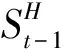

(2)

2 GARCH指标
由上述可知,统一阈值指标中u是一个固定值,这与实际情况不相符,因为在真实世界中,每个时间点的不确定范围通常不是一个统一值,而是随着时间的变化不断发生改变。由图1可以看出,区域A数据波动明显,而区域B数据波动较为平缓。区域A和区域B数据的波动规律不一致,在进行数据的表示时不能使用统一的概率密度方程笼统代替。通过进一步研究发现,在进行一个概率密度函数推算时,底层的描述模型加入均值和时变方差能够很好地提高数据描述的精度,由此提出了GARCH密度指标的概念。

2.1 GARCH模型

(3)

(4)

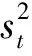
(5)

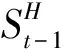
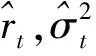
1.推算模型ARMA(p,q),得到ai,其中t-H+max(p,q)≤i≤t-1
2.根据ai推算模型GARCH(1,1)

4.ub←rt+kσt,lb←rt-kσt
2.2 加强的GARCH模型I-GARCH
在实际中,时间序列通常存在噪声点或者错误值,例如传感器错误、网络断开等。上述提出的GARCH模型只适用于处理数据精确的不确定时间序列,对于包含错误数据的时间序列没有很好的性能。为了解决这一问题,提出了一种加强的GARCH密度指标I-GARCH(improved GARCH)。
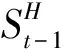

图2 ARMA-GARCH和I-GARCH举例说明

3 I-GARCH动态指标的改进
尽管在现实中,一条时间序列连续出现错误值的可能性很小,但是为了确保数据的精确性,提出了一种新的方法,用来过滤I-GARCH模型中的错误值,称为错误值过滤算法EVF(erroneous value filtering)。
算法的输入为包含错误值的时间序列V=[v1,v2,…,vk]以及阈值参数DTmax和Emax。具体的实现步骤如下:
(1)计算记录了一条时间序列V中,两两相邻的数据之间的差值;
(2)遍历差值集合,根据DTmax判断该差值是否在允许范围内,如果小于阈值参数,默认该数值为正确值;如果差值大于阈值,则继续遍历;
(3)如果连续出现差值超过阈值的情况,记录出现的次数,如果该次数大于Emax,则认为这些连续的点并非错误值,而是时间序列的走势发生了明显的变化,原始数值不作变动,继续向下遍历;
(4)反之,当记录的次数在阈值范围内,则说明该点为异常点。找到该点在序列中的位置,将其删除。并通过线性插值的方法计算新的值代替原有错误值。
算法2:EVF
输入:包含错误值的时间序列V,差值阈值DTmax,连续错误个数阈值Emax
输出:干净值序列V
李顺过来说,六如叔,你怎么这么拧呢,社区开发那是乡里开会订下的,你那个合同也不顶事。再说,还是人家佟老板救了你,你总不能恩将仇报吧。
1.ArrayList
2.int differ=0;int count=0;
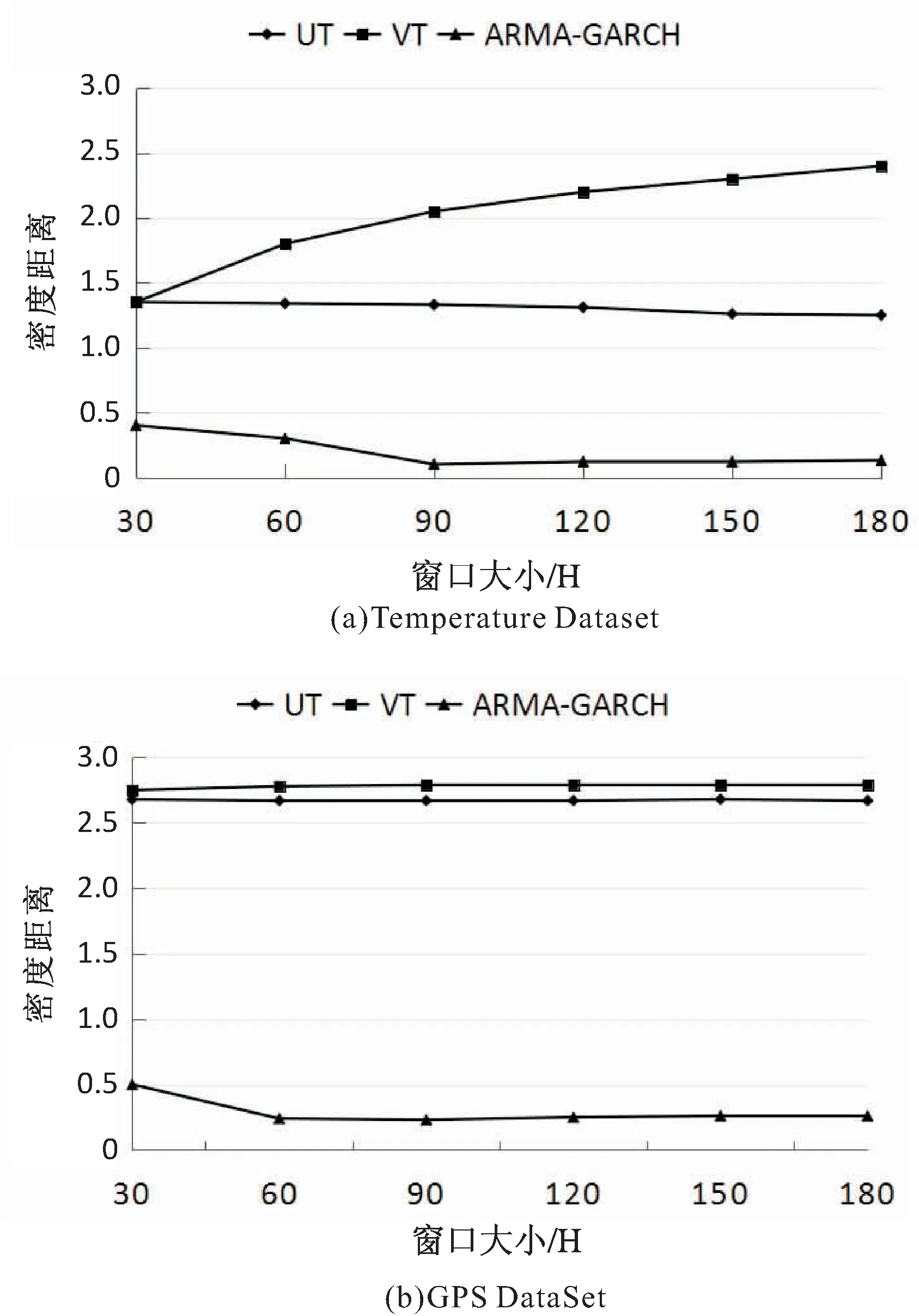
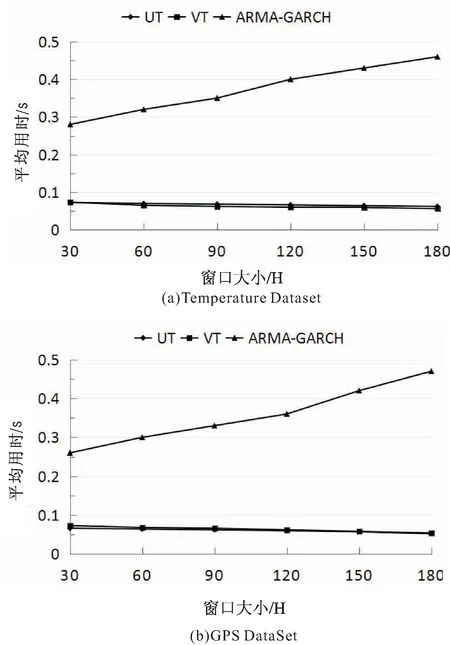
3.for(int i=1;i 4.differ=abs(vi-vi-1); 5.differList.add(differ); 6.} 7.ArrayList 9.while(i 10.int count=0; 11.while(differList.get(i) 12.while(differList.get(i)>DTmax&& i 13.if(count 14.} 15.for(int i=0;i 16.Vi+1为错误值将其删除; 17.使用(vi+vi+2)/2线性插值代替Vi+1; 18.} 实验目的主要有两个:验证提出的动态密度指标ARMA-GARCH对于真实数据集有良好的准确性与高效性;比较ARMA-GARCH与I-GARCH,验证添加了错误过滤的I-GARCH模型对处理包含错误数据的数据集的优越性。 实验数据取自两个真实的数据集。一个是Temperature Dataset,该数据集记录了20天内传感器网络监测得到的气温变化的所有数据,约21 000条样本数据。另一个数据集为GPS Dataset。这个数据集包括从导航系统记录的192辆车的GPS日志。每一个日志元组包含时间和x-y数值,本实验只取用其中的x数值。该数据集包含约10 000条数据。两个数据集的详细情况如表1所示。 表1 实验数据说明 (1)动态密度指标的衡量。 设p1(R1),p2(R2),…,pt(Rt)是用动态密度指标推导得到的概率分布序列,z1,z2,…,zt为相应的概率积分变换值。则只有当pt(Rt)等于真正的密度分布pi(Ri)时,z1,z2,…,zt才会均匀分布在(0,1)之间。实验使用直方图近似法验证z1,z2,…,zt的累计分布方程,判断其是否为均匀分布,将其累计方程定义为Oz(z),同时定义在(0,1)上均匀分布的标准累计方程为Uz(z)。定义Oz(z)和Uz(z)之间的差距为密度距离,表达式如下: 密度距离可以量化地测量观察值分布,z1,z2,…,zt和它们的预期分布之间的差距,因此可以作为衡量动态密度指标的标准。 (2)实验过程。 第一部分:动态密度指标的比较。 将提出的ARMA-GARCH与统一阈值和可变阈值进行比较。所有的评估都在两个数据集上进行。使用密度距离作为衡量各个动态密度指标质量的标准。同时,也比较了各动态密度指标的运行效率,以运行时间作为衡量的标准。 第二部分:I-GARCH和ARMA-GARCH的比较,实验在Temperature Dataset上进行验证。为了比较两个指标对于处理数据的精确性,在原有数据中插入人工合成的错误数值,即随机地在原始数据中插入数值远高于或低于正常范围数据的数值。以捕获错误值的数目和运行时间作为衡量两个指标优劣的标准。 (1)第一部分的实验结果。 图3 动态密度指标比较 图3显示了随着窗口尺寸(H)的增大,各种动态密度指标在两个数据集上的密度距离的比较。从图中可以明显看出,MARA-GARCH优于原始的动态密度指标。 图4显示了执行一次密度推算迭代所需的平均时间。由图中可以看出,虽然ARMA-GARCH的执行时间总体上超出原始动态密度指标,但是差距并不明显,大约在0.2~0.4 s左右。考虑到其在准确度和效率上的优势,ARMA-GARCH仍是性能最好的动态密度指标。 图4 动态密度指标效率比较 (2)第二部分的实验结果。 图5 I-GARCH和GARCH的比较 综上,文中提出的ARMA-GARCH模型及I-GARCH模型与已有的统一阈值指标(UT)以及可变阈值指标(VT)相比具有很大的优势,可以准确地推算出不确定时间序列的概率密度分布,在准确度和时间消耗上优势明显;同时,优化了I-GARCH指标,提出的算法EVF可以很好地检测出不确定时间序列中的错误值,进行错误值的清洗与替换,具有良好的容错性和一般通用性。 不确定时间序列的概率分布随着时间的变化而不断改变,无法使用已有的概率数据库生成方法直接对其进行数据库生成操作。因此在进行数据的存储之前,需要对原始数据进行有效的概率分布推导工作,得到不确定时间序列数据随着时间变化的一般分布规律。文中依托已有的ARMA模型和GARCH模型,提出推导不确定时间序列概率分布的ARMA-GARCH模型以及I-GARCH模型,并且在此基础上进行进一步的改进,提出能有效过滤错误值的算法EVF。实验结果表明,ARMA-GARCH模型和I-GARCH模型能有效地根据时间序列的发展规律推导得出正确的概率分布。同时,针对包含错误数据的数据集,EVF算法体现出高效的错误排查功能,具有良好的容错性和一般通用性。下一步的研究工作是利用推导得出的概率分布生成不确定时间序列的概率数据库。4 实 验
4.1 实验目的
4.2 实验数据

4.3 实验方法
4.4 实验结果与分析
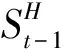


5 结束语
