一种平面正则C-Bézier曲线的广义偏距曲线构造方法

谭 振，李军成



一种平面正则C-Bézier曲线的广义偏距曲线构造方法

谭 振1，李军成2*

（1. 湖南省农村信用社联合社，湖南 长沙 410079；2. 湖南人文科技学院数学与金融学院，湖南 娄底 417000）

给出了一种平面正则C-Bézier曲线的广义偏距曲线构造方法。该法首先依据C-Bézier曲线的de Casteljau算法求出C-Bézier曲线各点处的单位切矢，然后即可自然生成其广义偏距曲线。数值实例表明，该法计算简单，且效果较好。

等距曲线；广义偏距曲线；C-Bézier曲线

0 引言

等距曲线在工业领域有着广泛的应用，如数控机床加工过程，机器人行走路线等与CAD/CAM相关的领域[1]。关于Bézier曲线的等距曲线，已有文献对此进行了研究。例如，文献[2]给出了用三次PH曲线构造平面Bézier曲线的等距线算法；文献[3]研究了圆域Bézier曲线的等距曲线；文献[4-7]从不同角度研究了Bézier曲线的等距曲线的有理逼近方法；文献[8]讨论了Bézier曲线的等距曲线的同次多项式逼近方法。

然而，在工程应用中由于实际问题的需要，必需扩展等距曲线的定义，如文献[9]利用曲线上各点的切向量和法向量所形成的局部坐标系来确定等距方向，给出了一种广义偏距曲线的定义；文献[10]利用de Casteljau算法构造了平面正则Bézier曲线的广义偏距曲线。作为一种非多项式曲线造型方法，C-Bézier曲线[11]不但具有Bézier曲线的许多优点，而且能够方便、简洁、精确的构造二次曲线，在几何造型中获得了广泛的应用，因此构造C-Bézier曲线的广义偏距曲线也具有重要的应用价值。为此，本文给出了一种平面正则C-Bézier曲线广义偏距曲线的构造方法。该法首先给出了C-Bézier曲线的de Casteljau算法，并依此算法求得C-Bézier曲线上各点处的单位切矢，从而构造出平面正则C-Bézier曲线的广义偏距曲线，而其等距曲线则是广义偏距曲线的一种特殊情形。

1 C-Bézier曲线简介

C-Bézier曲线[11]的矩阵表达式可写为

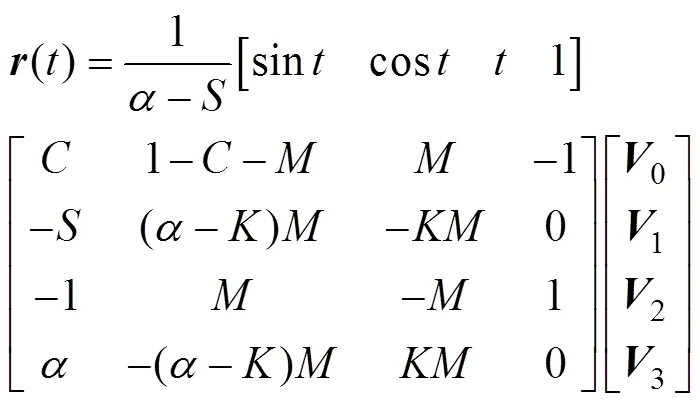
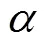
2 平面正则C-Bézier曲线的广义偏距曲线

2.1 C-Bézier曲线的de Casteljau算法

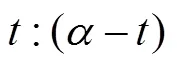
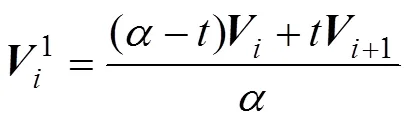
式中上标1表示第一次分割。第一次分割后，得到3个分割点，由其组成一个新的控制多边形，用相同的方法再对该多边形进行分割，可得到2个分割点为

上述分割过程可用C-Bézier曲线的de Casteljau算法表示如下

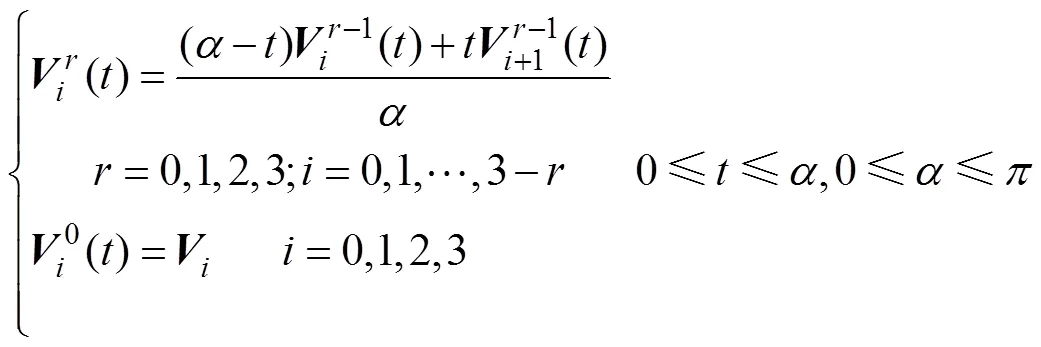
2.2 广义偏距曲线的构造

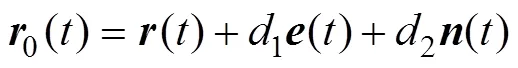
图1 广义偏距曲线的定义

Fig.1 Definition of the generalized offset curve

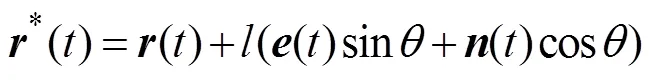
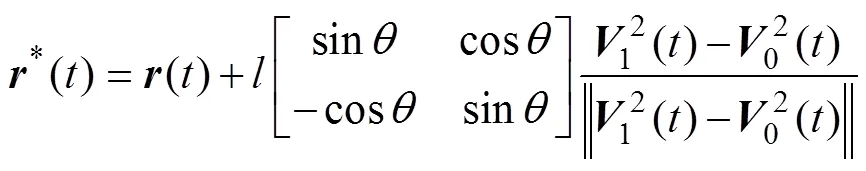
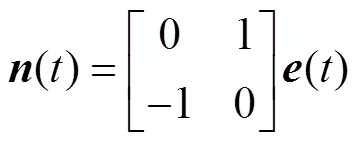
将式（5）代入式（3）有

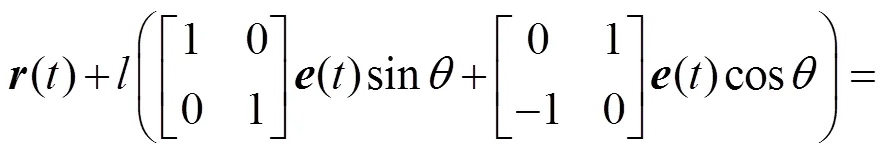
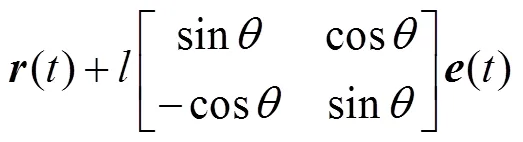
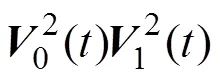
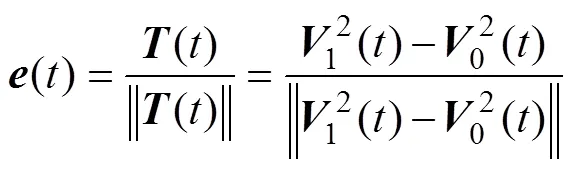
将式（7）代入式（6）即可得证。证毕。

由上述定理可知，构造平面正则C-Bézier曲线的广义偏距曲线的算法步骤如下：

3 数值实例

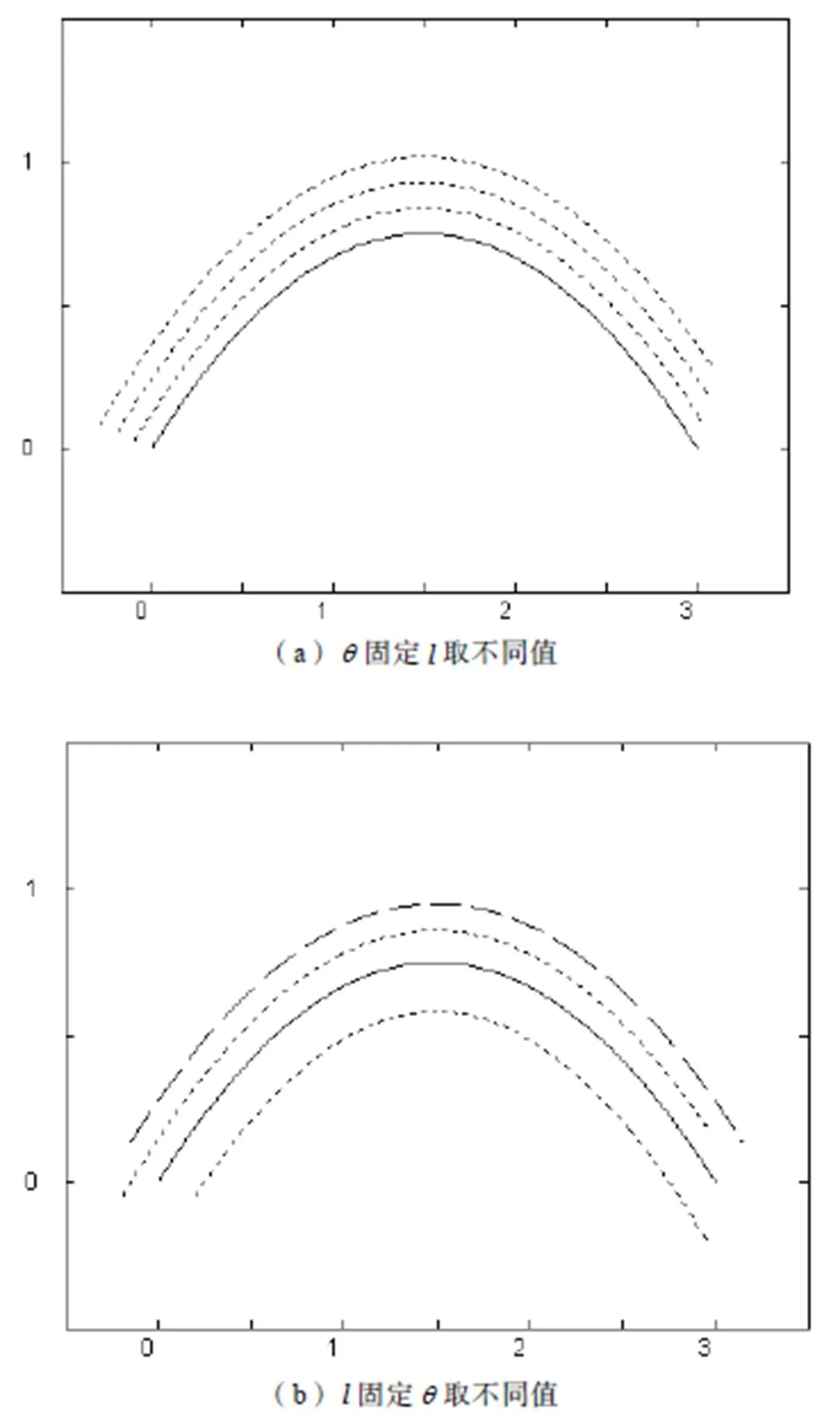
图2 C-Bézier曲线的广义偏距曲线

4 结语

本文主要讨论了平面正则C-Bézier曲线的广义偏距曲线的构造方法，该法主要依据de Casteljau算法求得C-Bézier曲线上各点处的单位切矢，然后根据定义就可自然构造出广义偏距曲线。最后，通过实例表明，利用该法构造C-Bézier曲线的等距曲线和广义偏距曲线时，其几何意义明显、计算简单，且效果较好，方便实际应用。

[1] Maekawa T. An overview of offset curves and surfaces [J]. Computer Aided Design, 1999, 31(3): 165-173.

[2] 郑志浩, 汪国昭. 用三次Ph曲线构造平面Bézier曲线的等距线算法[J]. 计算机辅助设计与图形学学报, 2004, 16(3): 324-330.

[3] 陈笑, 王国瑾. 等距曲线的圆域Bézier逼近[J]. 软件学报, 2005, 16(4): 616-624.

[4] 郭清伟. 等距曲线有理逼近的一种方法[J]. 应用科学学报, 2006, 24(3): 278-282.

[5] 张伟红, 檀结庆. 平面Bézier曲线的等距曲线有理逼近新方法[J]. 合肥工业大学学报(自然科学版), 2007, 30(5): 627-629.

[6] 江平, 王珺. Said-Bézier曲线的等距曲线的有理逼近[J]. 计算机辅助设计与图形学学报, 2008, 20(11): 1494-1499.

[7] 张莉, 檀结庆, 刘植. 等距曲线的S幂基有理逼近[J]. 合肥工业大学学报(自然科学版), 2008, 31(6): 956-958.

[8] 王珺, 江平. Bézier曲线的等距曲线的同次多项式逼近[J]. 计算机辅助设计与图形学学报, 2009, 21(9): 1251-1256.

[9] 陈雪娟. 广义偏距曲线及其性质[J]. 厦门大学学报(自然科学版), 2005, 44(3): 308-310.

[10] 严兰兰, 宋来忠. 正则 Bézier 曲线的广义偏距曲线及其 Matlab 实现[J]. 三峡大学学报(自然科学版), 2006, 28(4): 370-373.

[11] Zhang J W. C-curves: an extension of cubic curves [J]. Computer Aided Geometric Design, 1996, 13(3): 199-217.

A generalized Offset Curve Construction Method for Planar Regular C-Bézier Curve

TAN Zhen1, LI Jun-cheng2*

(1. Hunan Rural Credit Union Association, Changsha 410079, China; 2. College of Mathematics and finance, Hunan University of Humanities, Science and Technology, Loudi 417000, China)

A method for constructing the general offset curve of planer regular is presented. The unit derivatives of C-Bézier curve are computed by the de Casteljau arithmetic, then the general offset curve could be constructed naturally, which enriches the theories of C-Bézier curve. Some numerical examples show that the arithmetic is simple and effective.

Offset curve; General offset curve; C-Bézier curve

TP391

A

10.3969/j.issn.1003-6970.2018.11.002

湖南省自然科学基金资助项目(2017JJ3124)

谭振(1983-)，男，硕士，工程师，主要研究方向：计算机图形学、软件工程。

李军成(1982-)，男，博士，副教授，主要研究方向：计算机辅助几何设计及其应用、数学建模。

谭振，李军成. 一种平面正则C-Bézier曲线的广义偏距曲线构造方法[J]. 软件，2018，39（11）：07-10