一种铁磁物体固定磁性反演新方法

周国华，刘胜道，刘月林，隗燕琳

(1.海军工程大学 电气工程学院,湖北 武汉 430033；2.定海装备技术质量监测站，浙江 舟山 316000)

0 引言

与其它铁磁物体一样，由于磁滞效应，在地磁场作用下的钢铁结构舰船不仅存在着感应磁性，还存在着剩余固定磁性。感应磁性属瞬时效应，其计算技术研究相对较多；固定磁性属累积效应，与复杂的磁化历史有关，因而固定磁性的计算一直是个技术难题。

目前，固定磁性的研究工作还不是很深入，文献[1]用磁偶极子模型和遗传算法对舰船固定磁性计算问题进行了一定程度探索；文献[2]研究了薄壳简化船模的感应磁性与固定磁性混合模型，为舰载闭环消磁技术的研究奠定了基础，但由于其将自身固定磁性引起的感应磁性也纳入磁场模型的感应磁性范围考虑，因此其难以满足舰船磁性处理的技术需求。

由于磁化历史的缺失，求解固定磁性只能采用逆问题的思路，即依靠磁传感器测量得到部分磁场信息来反演计算铁磁物体的固定磁性。通常情况下，通过磁场测量只能获得固定磁性和感应磁性的合成磁场。因此，为实现铁磁物体固定磁性的求解，必须分2步：首先通过正演技术将铁磁物体的感应磁场分解出来；其次基于测量得到的合成磁场与计算得到的感应磁场之差，通过反演技术来计算铁磁物体的固定磁性。按照上述思路，本文提出了一种基于磁场积分法和截断总体最小二乘(Truncated Total Least Square, TTLS)正则化方法的铁磁物体固定磁性反演技术，并用钢板固定磁性反演计算实验对其有效性进行了验证。

1 铁磁物体固定磁性反演计算原理

在图1所示的静磁计算问题中，磁化强度为M的铁磁物体在测量点处产生的磁感应强度可表示为M的函数

Bm=f(M)

(1)

用磁场积分法求解静磁问题时算子f可表示为[3]

(2)

为消除积分奇异性，算子f的体积分形式在均匀磁化条件下可简化为相应的面积分形式[2,4]

(3)

由铁磁学理论可知，在外磁场作用下的铁磁物体，其内部总磁化强度M可表示为由外磁场引起的感应磁化强度Mind和由磁滞效应产生的剩余固定磁化强度Mper之和，即M=Mind+Mper。因而，测量点处的磁感应强度可分为2部分，即由感应磁化强度产生的感应磁感应强度

(4)

和由固定磁化强度产生的固定磁感应强度

(5)

通常情况下，感应磁化强度和感应磁感应强度都可以通过正演方法计算得到，但固定磁化强度和固定磁感应强度只能通过反演技术进行计算。为求得铁磁物体的固定磁性，可建立下列固定磁性反演模型

(6)

AMper=b

(7)

式中A称为系数矩阵，由算子f决定。求解上述反演模型就可解算铁磁物体的固定磁性。然而，与其它应用领域的逆问题一样，由于测量信息的不足，反演模型(7)常表现出很强的病态性。测量数据中较小的测量误差或感应磁感应强度中较小的计算误差都可能引起固定磁性反演计算的较大波动。正则化方法为提高反演模型计算结果的稳定性提供了手段。

2 固定磁性计算的各主要算法实现

从上述固定磁性计算原理分析过程中，不难发现求解铁磁物体固定磁性的关键在于测量点处感应磁感应强度的正演计算和固定磁性反演模型的病态性处理，下面我们主要来研究有关这两方面的具体算法实现过程。

2.1 感应磁性的正演计算

为实现测量点处感应磁感应强度的计算，首先需计算铁磁物体内部的感应磁化强度。不妨将铁磁物体离散为N个六面体单元，当各离散单元足够小时，其内部磁性参数可看作常数。以各单元中心为场点，根据总场B与磁化场Bm及源场B0的关系

B=Bm+B0

(8)

及场量关系式

(9)

则有

B(rpj)=-μrjB0(rpj)

(10)

式中：j=1,2,…,N；μr为铁磁物体的相对磁导率；B0为外加磁化场。求解式(10)，结合式(9)和式(4)即可实现铁磁物体在测量点处感应磁感应强度的计算。

2.2 固定磁性反演模型的病态性处理

随着逆问题模型在各实际工程领域的出现，病态逆问题的求解方法也得到了深入研究。正则化技术能够有效抑制数据误差对病态逆问题计算结果的影响[5-9]。常用的正则化方法有截断奇异值分解法、Tikhonov正则化方法和迭代正则化方法等，这类正则化方法的缺点是仅考虑了反演模型数据项含误差的情形。在固定磁性反演模型中，不仅反演模型右端数据项中存在误差，而且磁传感器位置误差、系数矩阵中各元素积分计算误差都会给模型系数矩阵带来误差。考虑到截断总体最小二乘法(Truncated Total Least Square, TTLS)能够有效处理病态反演模型两端都存在误差的情形[10]，本文将其应用于固定磁性反演模型的求解，以提高反演计算的精度和稳定性。

TTLS是在用总体最小二乘法(Total Least Square Method, TLS)求解逆问题的基础上提出的。用TLS法求解逆问题离散模型时，同时考虑系数矩阵A和测量数据向量b中都存在误差的情况。TLS的基本思想是用误差向量Δb干扰测量数据向量b、误差矩阵ΔA干扰系数矩阵A，以校正A和b两者同时存在的误差，即将式(7)转化为求解下列优化问题

(11)

s.t.(A+ΔA)Mper=(b+Δb)

式中‖·‖F为矩阵Frobenius范数。对增广矩阵[Ab]作奇异值分解，有

(12)

从而可得式(11)的解[11]

(13)

(14)

可得逆问题模型(7)的TTLS解

(15)

正则化参数k的选择决定着解的抗误差干扰能力和计算精度，可由L曲线法或广义交叉检验法来确定。本文采用L曲线法来确定正则化参数，L曲线的横坐标和纵坐标分别取为

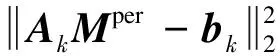
3 钢板固定磁性计算实例

3.1 钢板磁场原始数据的测量

为实现钢板固定磁性的计算，设计了图2所示的测量点方案。钢板尺寸为1 000 mm×200 mm×6 mm，相对磁导率140。在钢板受外磁场B0=-34 500exnT纵向磁化的条件下，采用测磁精度为10 nT的三分量磁通门传感器测量得到了图2所示41×5平面点阵上的磁感应强度数据B1，并以该磁场数据来进行钢板固定磁性的建模计算。

为对计算结果进行评估，在钢板分别受外磁场B0=-34 500exnT和B0=34 500exnT的磁化条件下，测量得到了距离钢板582 mm的下方平面33×2点阵上的磁感应强度数据B2和B3，以分解出钢板感应磁场和固定磁场测量值，即

3.2 钢板感应磁性正演计算

为求解钢板感应磁性，将钢板离散为100个六面体单元，如图3。感应磁场正演计算模型(10)中各参数的计算可参见文献[4]。图4和图5分别给出了钢板内部感应磁化强度分布和测量点处感应磁场Z分量计算值和测量值对比曲线。由图可以看出，感应磁场Z分量计算值与测量值之间具有很好的一致性，其计算误差为6.7%。

3.3 钢板固定磁性反演计算

在求解上述感应磁场的基础上，基于磁场测量数据B1建立了如下固定磁性反演模型

(16)

3.4 讨论与分析

钢板固定磁性反演结果表明，在钢板较粗略的剖分下，其固定磁性计算就可达到满意的计算精度，从而说明本文算法能够有效重建铁磁物体固定磁性分布。从其整个建模过程可以看出，其误差来源主要为原始磁场测量误差、感应磁场计算误差及反演模型病态性处理引入的舍入误差。这些误差的消除，可有效提高固定磁性反演计算的精度。

4 结束语

本文提出了一种基于磁场积分法和TTLS正则化方法的铁磁物体固定磁性反演技术，为解决铁磁物体固定磁性计算提供了一条技术途径。钢板固定磁性计算实例表明，该方法能够根据磁场测量数据，有效重建其内部固定磁性分布。该方法对研究舰船等铁磁物体的固定磁性分布与提高舰船磁防护水平具有重要意义。