考虑换代周期影响的制造/再制造生产优化决策
2018-12-19钟精诚杜百岗郭顺生
钟精诚,郭 钧+,杜百岗,郭顺生
(1.武汉理工大学 机电工程学院,湖北 武汉 430070; 2.武汉理工大学 湖北省数字制造重点实验室,湖北 武汉 430070)
0 引言
市场经济的快速发展迫使制造商不断推陈出新以获得更大的市场份额,频繁的升级换代导致产品生命周期缩短,使大量产品在使用寿命未终结时便遭淘汰,这在造成资源浪费的同时也给人类生存环境带来了巨大危害。传统的废旧物品处理方式已经不适应循环经济发展的需要[1]。再制造作为一种废旧产品回收处理的高级形式,可以有效实现资源优化利用、环境保护和经济持续发展的综合目标,成为实现社会可持续发展最有效的途径之一。再制造的兴起使传统的生产系统逐渐由单一的制造体系转向制造/再制造的混合生产体系,既顺应了循环经济的潮流,也创造出了更大的利润空间。
市场需求日益多样化和个性化以及环保意识的普及,迫使企业逐步向多品种、小批量、快速更新换代、回收再利用等绿色混合制造模式转变。产品更新换代速度的加快,使得以电子产品为主的短生命周期产品制造/再制造离散型混合生产系统更具时变性。产品换代周期与生产系统中的多种决策变量具有复杂的耦合关系,给制造/再制造混合系统的生产决策带来了巨大的扰动,因此很难对制造过程和制造资源进行有效控制和合理利用。产品的换代周期指每一次升级换代的时间间隔,合理的换代周期能使市场供需关系形成良性循环,延长产品市场寿命,以获得更大的市场份额,防止产品废置过多造成直接的利益损失。因此,如何控制合理的换代周期对制造/再制造混合生产系统的优化生产至关重要。
市场竞争会缩短产品更新换代周期,对生产系统的决策产生干扰,主要体现在产品的库存协调[2]、定价策略[3-5]和需求预测[6-9]等方面。其中,Sarathi等[2]以短生命周期产品的市场特性为出发点,提出产品需求和库存的依赖关系,研究了不确定性需求和价格敏感条件下的库存协调与回购策略;SHU等[3]在考虑消费者偏好的基础上,解决了策略单盈利与总盈利两种模式下的短生命周期产品再制造协调定价决策模型;Ferrer等[5]研究了再制造生产系统中新产品和再制造产品的差异定价方法,在此基础上建立了再制造生产计划中的综合定价和生产规划模型。在对产品的需求扰动方面,徐琪等[7]提出传统和网络并行的双重销售渠道的概念,结合支持向量机(Support Vector Machine,SVM)算法和Bass模型研究了短生命周期产品的需求预测模型;在此基础上,谢建中等[8]以产品的特征相似度为核心,针对历史数据缺乏等特点在原有Bass模型上进行改进,实现了需求预测的进一步优化;Bernd等[9]通过时间序列的方式衡量每个规划周期的客户需求量,以此为基础研究了企业需求规划对生产计划的扰动关系,并以一种针对需求时间序列的自动选择和配置方法来提高需求预测的准确性。
目前,已有大量学者针对生产系统中的各种不确定情况提出了多种决策模型[10-24]。在对产品质量的不确定性研究中,张晶等[10]以再利用的零部件为出发点,对质量不确定性和系统可靠性的关系进行建模分析,提出一种定量的生产系统可靠度计算方法;谢家平等[11-12]以产品质量水平为内生变量,引入产品降级率的概念,在制造/再制造混合生产体系中加入市场偏好的扰动,研究了多种市场模式下的优化生产决策;许民利等[13]对生产系统中的产品质量和支付意愿差异(Willing To Pay, WTP)进行研究,探讨了3种生产模式下的最优生产决策问题;Denizel等[14]认为产品回收率与再制造过程中的生产成本随着产品质量等级的降低而增加,从而将回收产品的质量分为多个等级,建立了再制造投入的回收品具有不确定的质量水平以及生产能力受限情况下的再制造生产决策模型。为解决市场异质需求及再制造加工成本带来的扰动,温海骏等[15]将补偿函数应用于无限维模型到有限维模型的转化,建立了再制造成本及市场需求等不确定性情况下的两阶段模糊再制造生产计划模型,并将逼近原则运用到粒子群优化(Particle Swarm Optimization,PSO)算法来求解模型;刘志等[16]将模块化水平作为再制造生产系统的决策变量,研究了再制造成本影响下的两周期生产决策模型;陈伟达等[17]提出零部件的再制造成本差异和市场需求等多种不确定性因素,分析了生产系统协同的再制造优化模型。针对再制造过程中回收量和再制造率的时变性,丁雪峰等[18]分析了再制造率随市场定价的变化规律,建立了变动市场规模下的两阶段再制造产品定价优化模型;景熠等[19-21]提出回收率及再制造率等不确定性因素,将再制造产品的需求差异和替代作用加入传统的制造/再制造混合生产模式中,设计了一种双倍体遗传算法(Genetic Algorithm, GA)与自适应机制相结合的求解方法;Silva[22]将产品的市场需求和可回收量作为生产系统扰动的核心因素,利用等价原则将系统中的随机性问题转化为等价的确定性问题,以求解主变量约束下闭环系统的线性随机库存生产规划问题。对于生产中不确定交货期的处理,Zhang等[23]以生产的时变性为主导,研究了生产能力限制下无延期交货的生产计划模型,并采用启发式GA代替传统的分支定界算法,该算法对多周期大规模的生产决策问题有更好的求解效率;张守京等[24]提出一种价格分担和滞销回购并存的联合契约,综合考虑不确定交货期和时变性价格,建立了风险规避下的系统最优决策模型。
上述研究针对不同情形下再制造的生产优化问题,具有重要的借鉴意义和指导作用,但很少考虑变动的产品换代周期对制造/再制造系统混合生产系统的影响。由于换代周期涉及整个生产过程中的诸多因素,使得混合生产系统更加复杂多变,具体表现如下:
(1)阶段性影响 在产品的全生命周期中,每一次升级换代都会对生产系统产生阶段性影响。将产品的市场生命周期划分为多个阶段的升级换代过程,以变动的产品换代周期为切入点将会使决策过程更符合生产实际。
(2)多重不确定性 生产过程中产品的质量差异、销售阶段产品的定价和市场需求的变化,以及回收阶段的产品回收量与再制造率的时变性等,都是影响混合生产系统的重要因素,而且这些因素之间并不相互独立,例如回收产品的质量会影响再制造成本与再制造率[17],市场需求与产品价格也是动态调节关系[25],产品的换代周期与生产系统中各影响因素的相互耦合,进一步增加了决策中的不确定性。
综上所述,本文在产品质量和需求差异等影响因素的基础上,建立了变动的产品换代周期下的短生命周期产品制造/再制造生产决策模型,并采用基于混沌映射的遗传人工鱼群算法(Chaos-based hybrid Algorithm of Artificial Fish and Genetics, CAAFG)对模型进行求解。
1 问题描述及混合生产决策模型
1.1 问题描述
在激烈的市场竞争下,适时推出新产品能有效提高品牌竞争力与市场地位,这也对混合制造系统中各生产要素配置的合理性提出了更高的要求。因此,制定合理的产品换代周期成为生产决策中重要的一环。本文研究的是稳定的市场结构下,考虑产品换代周期的影响,由一个原始制造商和一个再制造商共同参与再制造的混合生产系统决策模型。
再制造指采用先进制造技术对回收的废旧产品中可修复的零部件进行改造,使其在性能上达到或者超过新产品,以达到再次利用的目的。本文所研究的再制造生产系统如图1所示,回收的上一代废旧产品经过可再制造性检测后,将所有符合要求的产品投入再制造,对不符合要求的产品进行报废处理,其中符合要求的部分占回收总量的比重为可再制造率。原始制造商和再制造商共同参与再制造,同时制造商还进行新一代产品的生产。
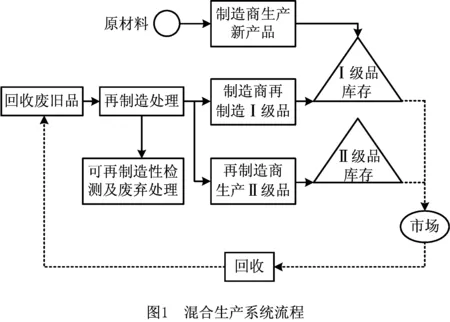
根据本文研究的模型作如下假设:
(1)制造商生产新一代产品的同时还进行再制造,在再制造产品的生产中,由原始制造商生产的再制造品质量优于再制造商生产的再制造品质量,为方便说明,将制造商生产的产品称为Ⅰ级产品,将再制造商生产的再制造品称为Ⅱ级产品。
(2)将再制造成品数量与投入量的比值称为再制造率。假定制造商的再制造率高于再制造商。
(3)制造商和再制造商生产同种型号的产品。
1.2 参数定义
考虑到函数和模型描述的简洁性,将文中涉及的符号变量及参数作如下说明:
u为产品型号,u=1,…,L,表示生产L种型号的产品;
m为制造商;
r为再制造商;

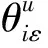
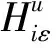
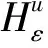
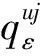
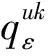
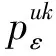
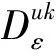
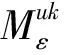
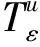
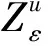
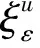
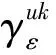
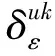
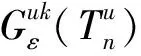
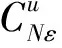
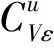
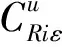
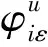
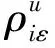
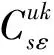
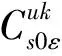
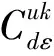
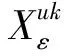
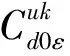
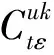
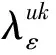
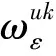
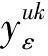
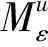
1.3 生产决策模型
本文在已有生产决策研究的基础上,考虑不确定的产品换代周期带来的阶段性影响,以及生产系统中各影响因素复杂关联导致的多重不确定性,以新产品和再制造产品的产量、市场定价、质量系数和产品换代周期为决策变量,以生产系统利润最大化为优化目标,建立了制造/再制造混合生产决策模型。为方便模型的构建,现将各决策变量之间的联系说明如下:
1.3.1 质量水平
产品的每一次升级换代都是在旧产品的基础上做相应的提升,依据可靠性和经济性对产品进行质量评价[25],并以此设定对新产品的质量要求,新产品必须满足新的性能和质量要求才能被投放到市场中,这样才能在与市场现存产品的竞争中获得优势,从而获得经济效益。产品的换代周期越短,一定时间内产品的质量改进次数就越多,产品质量升级不仅影响市场需求变化,还直接增加了研发成本[12]。因此,有必要对产品的质量水平进行合理控制。
1.3.2 市场需求
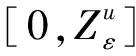
(1)
(2)
其中Dkε为第ε代k类产品市场需求受价格影响的部分,在市场经济下,Ⅰ级产品和Ⅱ级产品互为等价物,因此其市场需求由产品偏好系数和双方价格共同决定,有[26]:
(3)
(4)
1.3.3 生产成本
生产过程中的成本包括生产新产品的成本、废旧产品回收成本(包含可再制造性检测成本)、再制造生产加工的成本、产品滞销导致的库存成本、缺货导致的延期成本,以及产品升级所增加的研发成本。单位回收成本是预先可知的。
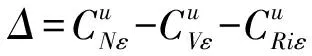
(5)
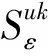
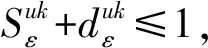
(6)
延期成本
(7)
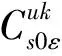
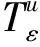
(8)
1.3.4 目标函数
在混合生产系统决策模型中,各决策变量之间的联系错综复杂,换代周期对系统的影响贯穿了产品从生产设计到销售的整体流程,为更好地体现变动的产品换代周期对混合生产系统带来的不确定性和阶段性影响,将系统总利润作为目标函数表示如下:
s.t.
(9)
(10)
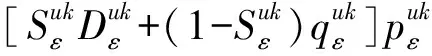
2 基于混沌映射的遗传人工鱼群混合算法
2.1 算法介绍
目前,许多智能优化算法,如PSO算法[27]、反向传播(Back Propagation,BP)神经网络[28]、蚁群优化(Ant Colony Optimization,ACO)算法[29]、GA[30]和人工鱼群算法(Artificial Fish-Swarm Algorithm, AFSA)[31]等,已广泛应用于包括生产调度和资源配置在内的组合优化问题求解中,并取得了大量满意的结果[32-35]。PSO算法是模拟自然界鸟群觅食行为开发的一种并行进化算法,具有搜索速度快、效率高的优点,但每一次迭代都会以其中的较优值作为优化方向的依据,因此随机性不强,容易丢失全局最优解而陷入局部最优;BP神经网络算法可以充分利用网络的反馈信息,实现任意线性或非线性的函数映射,但需要提前使用大量实验样本进行训练,而本文所研究的问题中没有足够的先验知识来确定神经网络的结构;ACO算法是一种具有正负反馈机制的启发式全局优化算法,具有很强的方向性,在旅行商问题(Traveling Salesman Problem, TSP)等复杂路径搜索问题上有很好的优化效果,但由于算法前期的信息素浓度较低,导致算法的收敛速度慢,求解效率较低;GA是一种群智能优化算法,是在交叉和变异操作中采用概率机制和多个体并行迭代的方式,其对函数的性态要求不高,且有较强的鲁棒性和全局寻优能力,但对初始种群有较强的依赖性,在迭代过程中容易产生对寻优过程产生干扰的非法染色体;AFSA能够实现算法的快速收敛,具有对初始种群和参数的选择不敏感、鲁棒性强、易实现等特点,在生产调度和资源分配方面都有较好的优化效果,但在当寻优域较大或处于变化平坦的区域时搜索性能劣化,导致搜索速度减慢。
本文提出的生产决策模型具有多重不确定性,无法在算法开始时获得高质量的初始值和参数。通过综合考虑各智能算法优缺点和本文所研究问题的特点,本文在AFSA的寻优基础上,采用基于混沌原理的Logistic映射加强局部搜索,将GA中的染色体与人工鱼状态等价,利用GA进行全局搜索。基于Logistic映射的混沌搜索能够实现区间内的无重复遍历,具有一定的随机性和规律性,可以提高算法的局部搜索能力[36-37],GA的并行性特点使算法能够高效地进行全局搜索,同时将变异和交叉机制引入鱼群行为中,可以调整人工鱼群体结构,提高算法的收敛速度[30]。在算法的整体性上采用分段优化的思想,以适应度值Xline为界限,适当调整step和visual等参数,从而保证算法在后期能够跳出局部极值而寻求更好的全局最优值,并有效提高了求解精度。
2.2 算法步骤
在该生产模型的求解过程中,需要确定最佳的产品换代周期、市场价格、产量和质量标准,以达到系统整体利润最大的生产目的。模型假定由式(1)~式(4)对产品进行市场需求预测,由式(8)确定技术投入成本,以求解第1章中目标函数的适应度值,算法总体流程如图2所示。
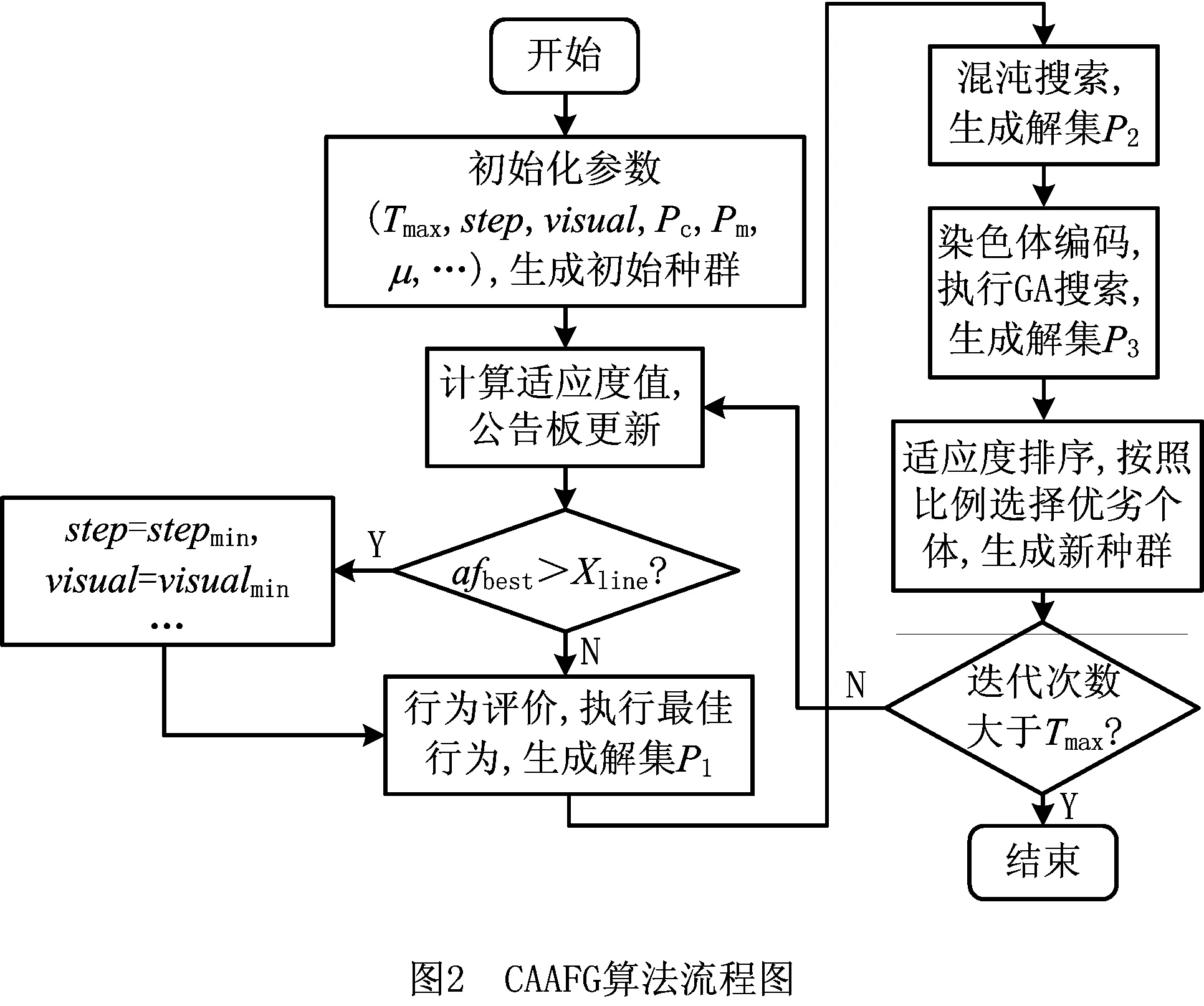
步骤1算法运行前的参数设定:算法最大迭代次数Tmax、人工鱼步长step、视野visual、尝试次数try_num、拥挤度因子delta、种群大小afmax、Logistic映射吸引子μ、初代混沌变量hd(0)、交叉概率Pc和变异概率Pm等。hd(0)为随机生成的7×u个(0,1)之间的不同初始值,且hd(0)中各值不能为{0,0.25,0.5,0.75,1}。
步骤2算法的初始解会对算法的收敛速度和收敛值产生一定影响,且初始值的生成需要满足一定约束条件,为保证算法良好的迭代环境,在各变量区间内随机生成afm条人工鱼(afm=1.2×afmax),将不满足条件的人工鱼重新初始化,最后按照适应度排序选择较优的afmax条人工鱼作为初始种群。其中每条人工鱼包含x1~x7七个参数,均采用实数编码的方式,各变量含义及编码内容如表1所示。
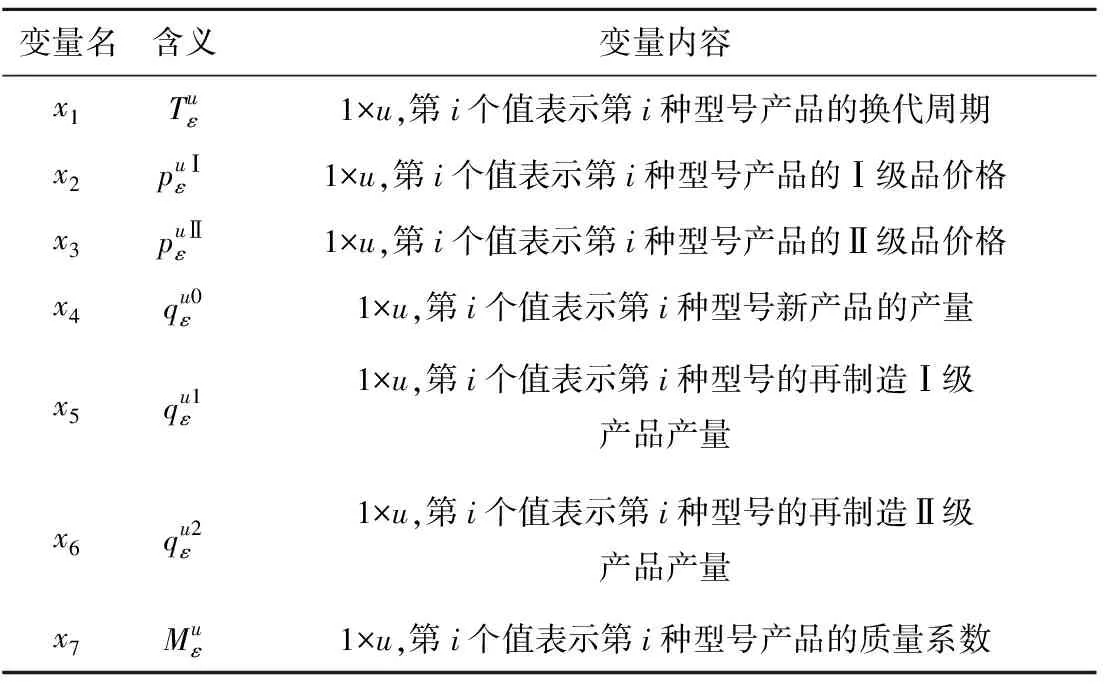
表1 变量含义及编码内容
步骤3按照适应度函数计算每条人工鱼的适应度值,并将最优值afbest记录在公告板中,作为公告板最优值。
步骤4参数更新判断。将公告板上的最优值afbest与Xline进行对比,若afbest>Xline,则更新step为stepmin,更新visual为visualmin,否则转步骤5。参数的更新是在算法快速收敛到一个较优的结果Xline之后,采用较小的visual和step来保证算法的精细搜索。其中Xline的设定是以普通鱼群算法的寻优结果为参照。
步骤5对每条人工鱼进行行为评价,模拟聚群(swarm)、追尾(follow)和觅食(prey)行为,选择适应度最大的行为执行,生成解集P1。可通过调整相应的参数对3种鱼群行为进行控制,采用较小的拥挤度因子delta或较小的尝试次数try_num增加鱼群行为的随机性,以跳出局部极值。每一条人工鱼执行最佳鱼群行为后,若其子代不满足边界条件,则以父代替换子代。
步骤6根据式(11)生成第k次迭代的混沌变量hd(k+1),然后根据式(12)在X1的基础上进行混沌搜索,生成解集P2。μ为混沌映射的吸引子,当μ=4时,可实现混沌映射的完全遍历。
Logistic映射公式为
hd(k+1)=μhd(k)(1-hd(k))。
(11)
混沌搜索公式为
P2=P1+(2hd-1)visual。
(12)
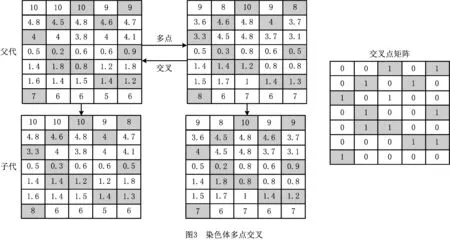
步骤7以P1和P2为初始种群,将鱼群参数实数编码为染色体,采用多点交叉和多点变异的方法,用GA进行全局搜索,得到解集P3。多点交叉操作中,按照Pc生成与染色体同等结构的0-1序列,将对应位置为1的基因点作为交叉点,变异点的生成方式与交叉点类似。详细的多点交叉过程如图3所示。
步骤8将P1,P2,P3按照适应度值排序,将当代最优适应度值thisafbest与afbest进行对比,若thisafbest>afbest,则将afbest替换为thisafbest。随后依照种群大小afmax,以9∶1的比例选择最优和最劣解,作为新的种群。
步骤9若公告板的最优值afbest满足精度要求,或者迭代次数达到设定的最大值Tmax,则输出afbest,算法终止,否则转步骤4。
CAAFG算法的伪代码如下:
0 最大迭代次数Tmax,人工鱼步长step,视野visual和其他相关参数初始化
1 令t=1,afbest=-inf,初始化种群afi,t,i=1,2,…,N,afbest为公告板最优值
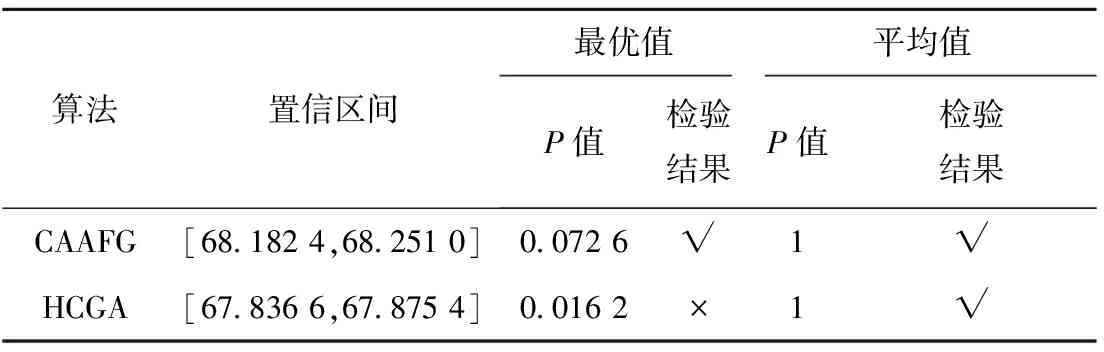
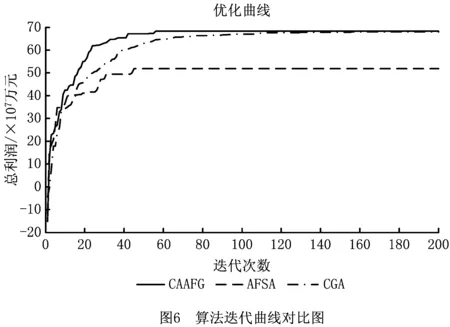
2 While t 3 计算个体适应度值并与afbest比较,将最优值记录在公告板上 4 If afbest>Xlinethen 5 Set step=stepmin,visual=visualmin; 6 End if 7 For all afi,tdo 8 For all afj,tdo 9 If dis(afi,t,afj,t) 10 记录视野范围内该人工鱼信息并计算适应度值foo(afj,t) 11 End if 12 执行鱼群行为move(afi,t),prey(afi,t),follow(afi,t),swarm(afi,t) 13 Set afi,t=move(afi,t) 14 If foo(prey(afi,t))>foo(afi,t)then 15 Set afi,t=move(afi,t) 16 Else if foo(follow(afi,t))>foo(afi,t)then 17 Set afi,t=follow(afi,t) 18 Else if foo(swarm(afi,t))>foo(afi,t)then 19 Set afi,t=swarm(afi,t) 20 End if 21 set afN+i,t=afi,t+(2hd-1)visual 22 End for 23 End for 24 For all afi,t(i=1,2,…,2N)do 25 使用锦标赛选择法选择个体 26 If random(0,1) 27 执行交叉操作 28 End if 29 If random(0,1) 30 执行变异操作 31 End if 32 根据9∶1的比例选择最优最劣解 33 End for 34 Set t=t+1 35 End while 36 Return afbest CAAFG的复杂度计算可将算法运行过程中主要执行步骤的复杂度相加。初始化总群需要N次赋值运算,复杂度为O(N);每个个体的适应度计算复杂度为O(L),在算法中对个体进行适应度计算并选择最优值的复杂度为O(L×N2);在执行鱼群行为的算法步骤中,查找视野内人工鱼与适应度值计算的复杂度最高,因此可将鱼群行为的复杂度视为查找视野内人工鱼与适应度计算的复杂度之和,其复杂度为O((aiL+N)×N),ai为第i个个体视野内的人工鱼数量,且ai≤N;同理,混沌搜索的复杂度为O(N),GA搜索中的复杂度为O(N×L×c2),c为锦标赛选择法每次选择的个体数,c≪N。综上,在最坏情况下(ai=N)对算法进行T次运算时,算法复杂度为O(T×(N+L+N2+L×n2+N+N×L×c2)),即为O(T×L×N2)。 为验证该算法的有效性,以国内某大型电子产品制造集团的制造/再制造混合生产计划为例,与混沌遗传算法(Chaos Genetic Algorithm, CGA)和AFSA组成一个对比实验。该集团的产品已进入市场多年,目前处于第六代产品的换代周期,在生产的准备阶段,该集团技术部研发出新一代产品后下发生产计划,由制造商和再制造商负责生产。制造商生产Ⅰ级产品,再制造商生产Ⅱ级产品。此次产品换代共生产5种型号的产品。表2所示为产品的技术投入系数以及新产品生产成本等数据,其中库存成本、单位时间损失成本以及消费者偏好系数是根据该集团的生产的历史数据做出的综合评估。以此为算例背景,在2.40 GHz CPU、Intel(R)Core(TM)i3-3110M处理器、4G RAM、Windows 7系统、C++语言和MATLAB R2013b的开发环境下对第1章提出的数学模型进行求解,并对算法性能进行实验分析。 表2 混合制造系统生产信息 算法参数对算法运行结果的影响不仅体现在搜索效率上,还体体现在会对求解精度和最优值搜索产生干扰。本文算法运行涉及诸多参数的选取,然而到目前为止,并没有系统的最优参数选取理论,因此本文通过多组不同的参数反复实验,逐步选取合适的step,visual,Pc,Pm和Xline等参数,对算法性能和可靠性作进一步实验分析。实验结果如图4所示,最终确定的CAAFG参数如表3所示,表4和表5分别为AFSA和CGA的初始化参数。 表3 CAAFG算法参数 NmaxTmaxstepvisualTry_numdeltaStepminvisualminPcPmμ502000.81.6200.30.30.80.650.014 表4 AFSA参数 表5 CGA参数 CAAFG是根据混沌搜索思想和GA全局搜索能力的优点,对单一AFSA的改进,并采用了阶段性的参数调整思想在算法的搜索效率和精度之间做出平衡。为更好地说明该算法的有效性,在相同背景下将CGA,AFSA和CAAFG进行仿真实验对比。在相同的实验环境下将3种算法运行20次,实验结果如表6所示。结果显示,AFSA算法的运行时间短,但是寻优结果精度较差,CAAFG和CGA均能获得较好的寻优结果,CAAFG的最优值优于CGA。 表6 实验对比结果 为进一步衡量在混沌映射的基础上对AFSA和GA进行混合改进的有效性及CAAFG算法的性能,在前文设定的实验环境下,选取其中性能较好的CGA和CAAFG两种算法进行30次重复仿真实验,运行结果如图5所示。从图中可以看出,CAAFG多次运行的收敛代数和最佳适应度趋于一致,具有较好的收敛稳定性。 在上述实验的基础上,采用显著水平为5%的T假设检验分析,具体假设如式(13)和式(14)所示。其中H0为零假设,H1为备择假设,θ0和θ1分别为置信区间内的集合和置信区间之外的集合,且二者无交集。结果如表7所示。 H0:θ∈θ0; (13) H1:θ∈θ1。 (14) 表7 T假设检验结果 对于本文所研究的生产决策模型,CAAFG和CGA均能获得较好的寻优结果,但CAAFG的最优值优于CGA,且在算法的时间复杂度和收敛性上也表现出了更好的寻优效率。从图6可知,在CAAFG算法的多次仿真运算中,其收敛代数和大部分的寻优结果均优于CGA,且其寻优结果也无较大波动,说明算法具有较强的收敛稳定性。在对实验数据的T假设检验中,CAAFG在基于平均值和最优值的检验中均能对原假设检验为真,而CGA只有在对平均值的检验中才能接受原假设,说明CAAFG求解结果的准确性优于CGA。综上,CAAFG算法在快速收敛的基础上能够获得比CGA更好的寻优结果,是一种有效的寻优算法。 在算法原理上,CAAFG引入了混沌搜索和GA的遗传变异操作,保留了AFSA收敛速度快的特点,获得了优于AFSA的求解精度和更好的全局寻优能力。其中,混沌搜索的遍历性加强了人工鱼在visual范围内的局部搜索,降低了丢失最优解的可能性;GA的多变交叉和变异实现了目标值的跳跃,脱离了step和visual的限制,能更好地搜索全局最优值;在新种群选择过程中,以9:1的比例选择当代最优和最劣解,避免了算法的早熟现象;在算法整体性上采用阶段性的参数调整,第一阶段采用较大的step和visual能够保证算法的全局搜索能力,第二阶段调整为较小的step和visual可以更好地平衡求解效率与求解精度。图6为3种算法最佳的适应度函数迭代曲线,从图中可知,CAAFG和CGA都能获得较理想的优化结果,具有良好的全局寻优能力,在算法收敛性方面,CAAFG和AFSA均能在算法前期快速收敛到最优值,具有良好的寻优效率。从表6的数据可知,因为CAAFG的复杂度高于AFSA,所以在运行时间上高于AFSA,但CAAFG能够获得3种算法中最优的求解结果,并且从平均适应度值和最佳适应度比例的数据上也证明CAAFG的稳定性优于其余两种算法。表8所示为该生产系统的初始生产计划和各算法寻优结果的数据对比,可见采用CAAFG的优化决策方案能比生产系统初始决策获得更大的系统总利润,且该方案优于其余两种算法求得的优化方案。 表8 制造/再制造混合生产系统决策优化结果对比 本文针对混合生产系统中的不确定性因素,提出不确定性换代周期的阶段性影响,以及各决策变量之间复杂耦合关系带来的多重不确定性,根据制造/再制造的生产特点制定了相应的数学模型,该模型描述了产品换代周期和市场价格等决策变量之间的内在联系,对系统的多重不确定性作了更加全面的分析,使得模型更加符合生产实际。然后采用一种基于混沌映射的遗传人工鱼群混合优化算法(CAAFG)对模型进行求解,该算法依据AFSA的不足,针对性地引入混沌理论和GA对单一AFSA进行改进,并将该算法与AFSA算法和一种改进的混沌GA进行多次实验对比,结果证明,该算法的全局最优值搜索和收敛稳定性均优于其余两种算法,具有一定借鉴意义。此外,本文研究了产品处于某一升级换代阶段的生产决策优化问题,对连续多个连续换代周期内的生产决策进行优化将是下一步的研究方向。3 应用算例
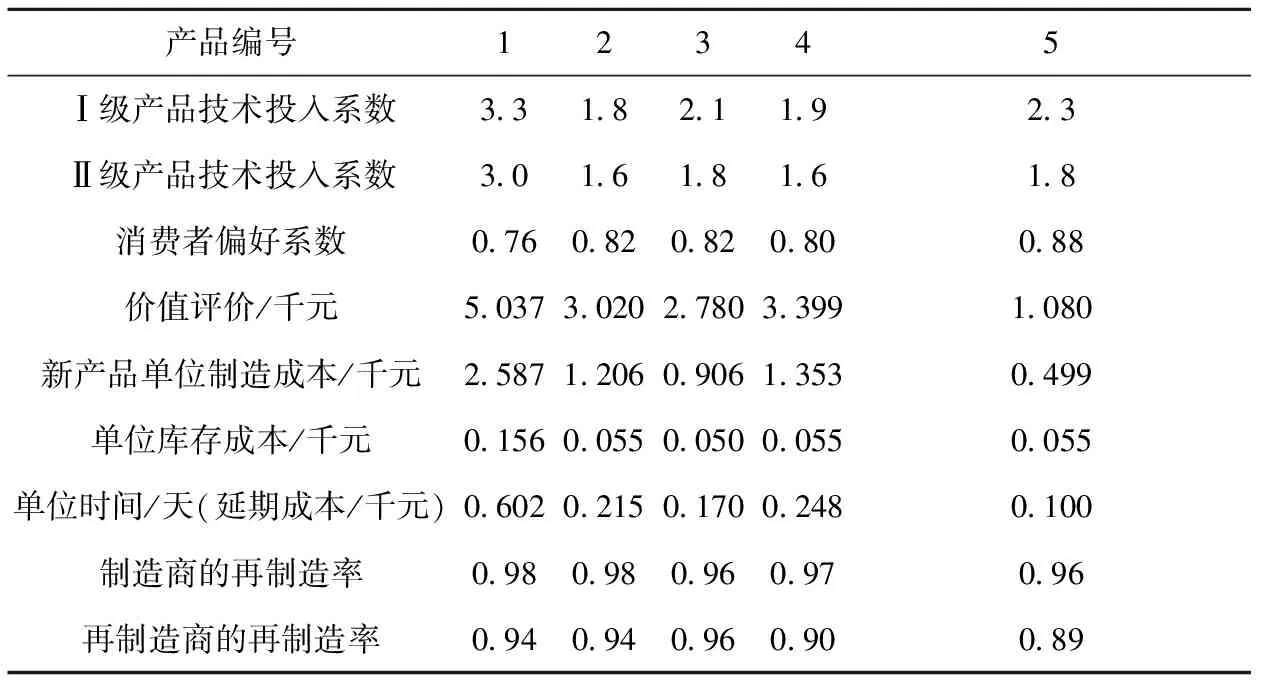
3.1 参数选取与性能分析
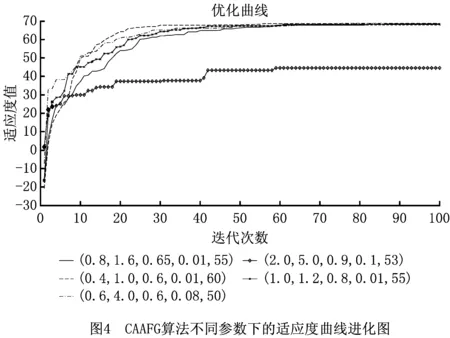



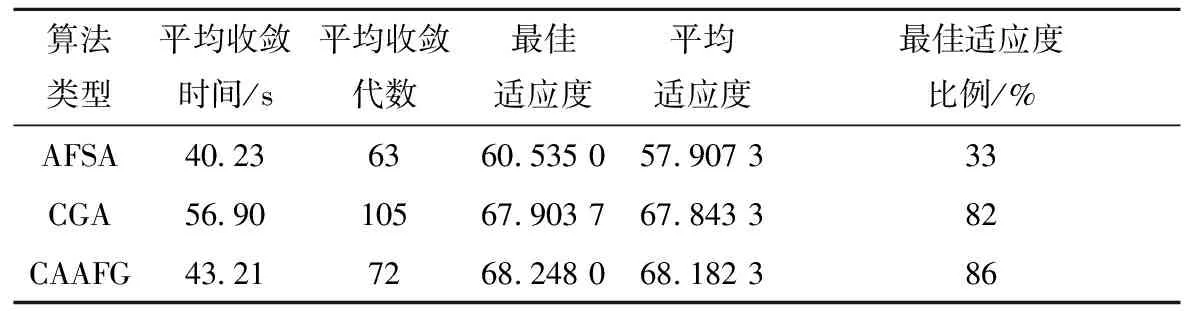
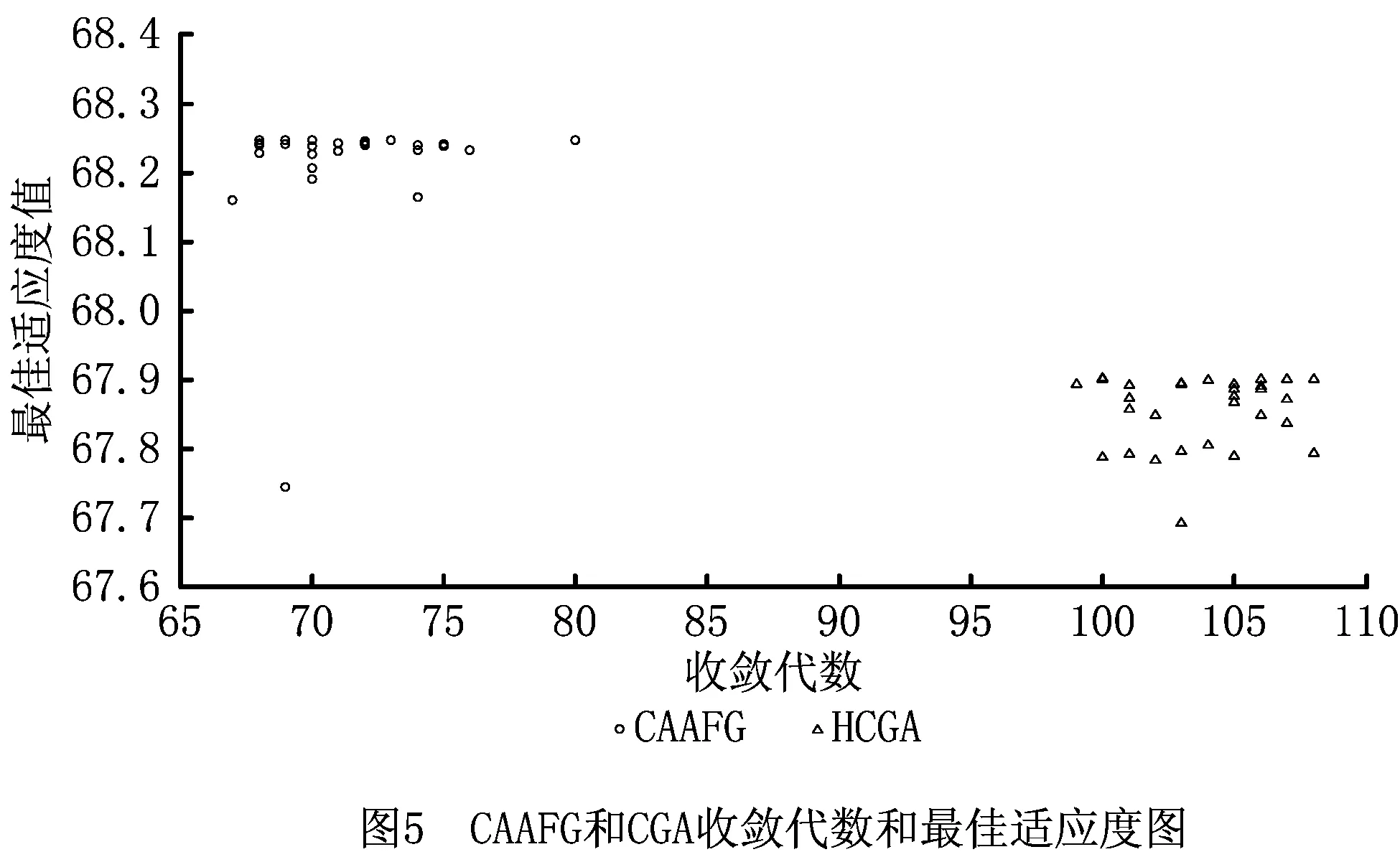
3.2 优化结果分析

4 结束语
